基于深度强化学习的无人机实时航迹规划
2024-01-18舒健生周于翔郑晓龙赖晓昌陶大甜
舒健生,周于翔*,郑晓龙,赖晓昌,陶大甜
(1.火箭军工程大学,西安 710025;2.武汉理工大学信息工程学院,武汉 430070)
0 引言
由于较好的机动性和灵活性,无人机(unmanned aerial vehicle,UAV)在战场打击任务、灾后搜索和救援任务等方面具有广泛的发展空间和良好的发展前景,UAV 需要较高的自主能力和实时航迹规划能力,以应对复杂多变的飞行环境,而国内外的研究主要集中于固定静态环境的无人机航迹规划问题。因此,无人机在获取动态变化的环境信息后,进行实时机动避障的能力变得尤为重要。当前解决航迹规划问题的传统算法主要包括:Dijkstra、A*算法、RRT*算法、粒子群算法、蚁群算法和人工势场法等[1-6],以及相关的改进算法。但是由于机载计算机的容量和计算能力有限,而传统路径规划算法的算法复杂度较高、计算量较大,无人机的实时航迹规划仍然是一个亟待解决的重要问题。
2013 年,DeepMind 团队利用神经网络的拟合功能,将观测到的高维环境数据拟合为Q 表[7],创新性地提出了DQN 模型,解决了对高维连续状态空间表征的问题,使深度强化学习成为人工智能领域的一个研究热点。强化学习算法相对于传统算法而言,泛化性更好,对动态变化的环境具有更强的适应能力,且能更好地满足在线航迹规划问题的实时性要求。目前,该算法在离线路径规划、在线路径规划,以及多智能体导航等方面都取得了不错的成果。郝钏钏等使用Q-learning 算法进行优化,设计连续回报函数,解决了奖励稀疏的问题,但容易产生数值抖动,算法收敛性不足[8]。王珂等将Q-learning算法与A3C 算法相结合,提出基于最小深度信息的有选择的训练模型,解决了由于动作选择缺乏针对性而导致算法收敛速度较慢的问题,但依然存在收敛不稳定的问题[9]。Q-learning 的状态空间和动作空间都是离散的,生成的航迹平滑性较差,与实际飞行情况的差别较大。
此后产生了一些效果更优、更稳定、收敛速度更快的算法,如:PPO 算法、SAC 算法和TD3 算法[10-12]。3 种算法各有优劣,其中,PPO 算法稳定较好,对参数的依赖较小,被Deep AI 公司设定为默认算法;TD3 算法在DDPG 算法的基础上进行改进,采用双Q 网络的形式避免了过估计情况的产生,其优化效果优胜于DDPG 算法;而SAC 算法是一种最大熵强化学习算法,能够探索到更多动作,有效避免了过估计情况的产生。徐国艳等设计改进人工势场法对agent 的位置进行评价,并将其作为过程奖励,大幅加快了PPO 算法的收敛速度[10]。GRANDO等在TD3算法和SAC 算法中分别加入了RNN 循环神经网络,使模型拥有了一定的记忆和推理能力,能参考前序信息更好地进行机动避障[11]。实验结果证明了改进算法的有效性,且改进后的SAC 算法收敛速度更快,效果更好。LEI 等采用带有预训练专家演示数据的TD3 算法进行路径规划,实验结果显示,改进后的算法在回合奖励值,平均成功率等方面都有较大提升,且显著降低了任务的失败概率[13]。这3 种算法的状态空间和动作空间都是连续的,与UAV的实际飞行情况更为贴近。
航迹规划问题是一个状态空间和动作空间都连续的问题。大量的研究和实验表明,具有Actor-Critic 算法框架的PPO、SAC 和TD3 算法能较好地解决此类问题,并且在收敛速度和稳定性方面优于其他算法。奖励稀疏是强化学习算法中存在的普遍问题。因此,本文基于智能体与目标区或最近障碍物几何距离变化设置连续奖励或连续惩罚,从而引导智能体快速向目标方向运动,并对障碍物进行有效规避。此外,UAV 在飞行过程中还需要满足自身飞行约束条件和环境约束条件,任务较为复杂,直接训练的难度较大,在单一环境中往往很难探索到有效动作,使算法的训练效率大打折扣。本文结合课程学习的方法,将上一个环境中保存的训练参数通过参数迁移的方式,加载到相应的强化学习算法中进行后续训练与学习。分阶段、分难度的学习方式,也使智能体在各训练环境中的动作探索更广泛、学习更加充分。因此,本文在此基础上对3 种算法设置分别进行改进、训练和比较,分析了各个算法进行二维平面的实时航迹规划的优点和不足之处。
1 相关算法
1.1 SAC 算法
SAC 算法是HAARNOJA 于2018 年提出的一种无模型的随机策略深度强化学习算法[12],其结构包括1 个actor 网络、4 个Critic 网络(状态价值估计V、Target V、状态-动作价值估计Q0和Q1网络)。传统的强化学习算法仅考虑最大化累计回报项,而SAC 算法同时最大化累计奖励项和策略分布的熵值项,熵值越大,动作的随机性越大,降低采样复杂度的同时提升了算法的探索能力和鲁棒性,防止算法过早收敛而产生局部最优解。
其中,R(·)为当前状态和动作下的奖励值项;H(·)为策略π 的熵值项;αH为温度系数,通过控制αH的大小确定策略分布熵值项的相对重要程度。


算法1 Soft Actor-Critic初始化参数images/BZ_138_425_1146_625_1189.png对每个训练回合执行:对每回合中的每一步执行:images/BZ_138_314_1289_765_1477.png结束对每个梯度执行:images/BZ_138_314_1577_766_1803.png结束结束
V Critic 网络更新的均方误差(MSE)损失函数为:
梯度:
此处梯度为无偏估计,D 表示经验池中的经验数据样本,at'为actor 网络根据当前状态st生成。使用随机梯度下降法更新得到的两个Q-Critic 网络的参数是不一样的,此处取两个Qθ的最小值进行计算可以显著加速训练。
Q -Critic 网络的更新同样是最小化MSE 损失函数:
梯度:
Actor 网络通过最小化KL 散度进行更新:
其中,Z(·)函数的作用是将分布进行归一化。
将策略用重参数化技巧表示为带噪声的神经网络:
梯度:
1.2 课程学习
课程学习是由BENGIO 提出的一种训练策略,模仿人类的学习过程,通过设置不同难易程度的课程来加速学习,从简单的问题学习到的策略迁移到复杂的问题中[14]。该方法被广泛应用于计算机视觉和自然语言处理等多种场景,以提高各种模型的泛化能力和训练效率。
在强化学习算法设计中,采用参数迁移的方式,把先前训练环境中训练好的模型参数迁移到当前训练环境中来,按任务难易程度进行多场景学习,对算法进行验证和比较。本文将UAV 航迹规划的训练环境拆分为多个,不同的环境对应不同的训练任务,有不同的训练目的。第1 个训练环境是空旷的自由运动空间,其目的在于使UAV 找到通向目标最近的路径。第2 个训练环境是包含障碍物的空间,在该环境中,UAV 逐渐学会规避障碍物并寻找到达目标的最近路径。
2 深度强化学习算法设计
2.1 网络结构
本文使用的深度强化学习算法包括3+n 个输入和1 个输出,如下页图1 所示。网络的输入为算法的状态空间,是agent 对环境空间进行观测得到的信息,是agent 进行动作选择的依据,包括3 个部分:目标相对位置Pg',agent 相对航程L'以及雷达在n 个方向上障碍物的距离信息PS';网络的输出为转角α。
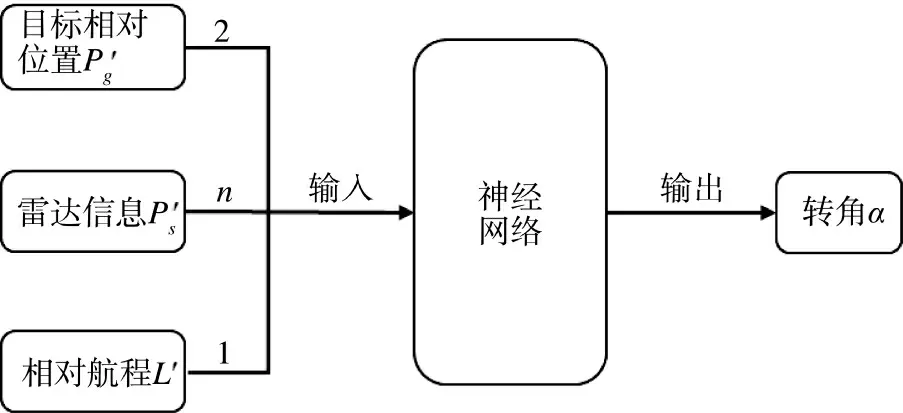
图1 输入输出结构图Fig.1 Input-output structure diagram
如图2 所示,SAC 算法的网络结构包括1 个Actor 网络、2 个结构相同的Q-Critic 网络、2 个结构相同的V-Critic 网络(其中一个为估计网络,一个为目标网络),其网络结构如图2 所示。Actor 网络、Q-Critic 网络和V-Critic 网络的隐藏层结构相同,均包含3 个隐藏层,每层为512 个节点的全连接层。Actor 网络的输入为agent 所在环境的当前状态st,输出为转弯角。Q-Critic 网络的输入为st和动作at,输出为当前状态动作对的Q 值。V-Critic 网络的输入为st,输出为当前状态值V(st),是对当前状态st的价值预测。
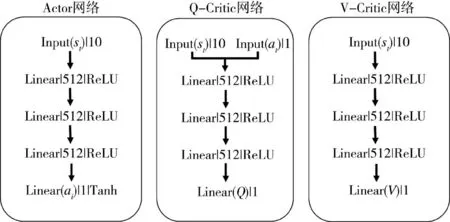
图2 网络结构图Fig.2 Network structure diagram
2.2 状态空间
2.2.1 目标点的相对位置关系Pg'
以飞行器坐标系下的目标点位置信息为输入将更有利于算法学习与目标点之间的相对关系。经过坐标系的平移和旋转变化,将目标点的原位置坐标转化到以无人飞行器(UAV)为原点,UAV 的飞行方向为y 轴,与y 轴水平垂直方向为x 轴的坐标系中。最后进行数值归一化处理,使Pg'各维的取值范围为[-1,1]。
其求解步骤如下:
首先,经过坐标系平移变换,将原坐标系原点平移至UAV 重心。
然后,如图3 所示,通过旋转矩阵,将目标点的位置坐标变换到飞行器坐标系上。

图3 坐标变换图Fig.3 Coordinate transformation diagram
计算公式如下:
其中,θu为飞行器的航向角;A 为旋转矩阵。最后,进行坐标数据的归一化处理。
2.2.2 相对航程L'
UAV 的飞行航程受最大飞行航程约束。将已飞航程信息与最大飞行航程的比值作为输入,可防止飞行器由于飞行航程过大或飞行时间过长而导致任务失败,从而确保飞行器更快接近目标区域。
2.2.3 雷达探测信息Ps'
在强化学习算法中,输入观察信息的维度不能过大,否则会导致算法学习速度缓慢,甚至造成神经网络学习困难,很难从输入中提取到有用的信息。但输入信息较少则算法的收敛效果将大打折扣。因此,需要在agent 的雷达探测范围内等角度θ取合适数量的探测方向,并设雷达的最大探测范围为Dmax=20,返回各方向与环境边界、障碍物之间的距离信息Di。
固定翼无人机只能向前方运动,因此以UAV的飞行方向为基准,在[-90°,90°]范围内的障碍物信息对于UAV 来说更有意义,本文兼顾算法的运算速度和训练效果,在该范围内按等角度30°取7个雷达探测方向,如下页图4 所示。
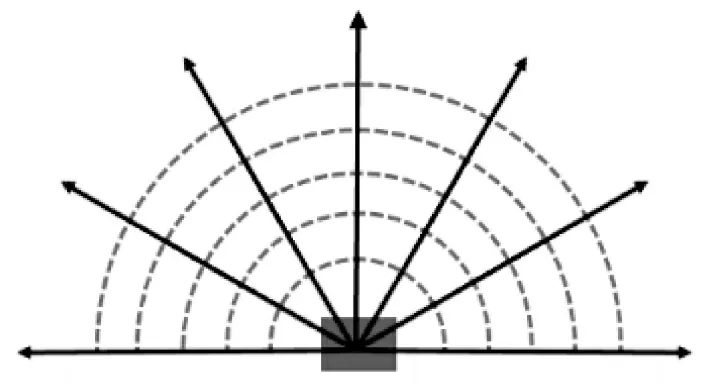
图4 雷达探测模型Fig.4 Radar detection model
2.3 动作空间
本文的研究对象为固定翼无人机,因此,其飞行过程中没有后退的动作。为使实验尽可能与实际情况相符合,将动作空间设计为连续动作,控制量为UAV 在航迹点处的转角大小。受自身气动特性的影响,UAV 在各航迹点处的水平转弯角不能超过最大转弯角的限制,否则会导致飞行器失稳,造成严重后果。如图5 所示,飞行器的实际转弯角α 受到最大转弯角αmax限制。

图5 UAV 转弯角示意图Fig.5 Schematic diagram of the turning angle of UAV
假设αmax已知,Ai为航迹段i 在x、y 坐标轴上的方向向量,其表达式为,则UAV 实际转弯角α 与αmax的关系如下所示:
在最大转弯角限制范围内,UAV 的转弯角越小,飞行轨迹的平滑度就越好,但机动性能会相应变差。因此,本文综合考虑各种因素,限制转弯角的取值范围为[-6°,6°]。
2.4 奖励函数
强化学习的奖励函数设置主要需解决稀疏奖励的问题,该问题广泛存在于实际应用中。稀疏奖励是指agent 在探索过程中很难获得正奖励,导致算法学习效率低下,难以探索到预定状态。本文的奖励函数分为3 个部分,并设置连续奖励,解决稀疏奖励的问题。
2.4.1 渐进奖惩Rd
设UAV 与目标当前时刻的距离为dt,为引导UAV 向目标运动,当时,表示agent在向目标点运动,给予agent 一个较小的渐进奖惩,其计算公式如下:
2.4.2 到达奖励Rar
为计算方便,本实验中将目标设定为圆形目标,目标半径为rg。则当agent 与目标中心的距离时,给予正向奖励Rar。
2.4.3 死亡惩罚Rde
UAV 的威胁源包括:静态固定障碍物、预警探测雷达以及防空武器等。与目标处理相似,将障碍物处理为二维圆形障碍物。分别以障碍物的最大半径、预警探测雷达的最大预警探测范围和防空武器的最大打击半径为威胁圆的半径rO。当agent 与目标中心的距离或agent 运动触碰边界时,给予负向奖励Rde。
2.4.4 总奖励值Rall
UAV 飞行总奖励为目标渐进奖励、到达奖励与死亡惩罚之和减去基线奖励(baseline)R0,如式(17)所示。基线奖励的添加可以让每步的动作有正有负,更有利于算法学习到优秀的动作。
3 飞行约束条件及参数设计
3.1 航迹段相关参数
在强化学习算法中,agent 每经过一个时间间隔Δt,对应做出一个动作(action),表示完成一步(step)。由于UAV 受自身性能参数和气动特性的限制,二维航迹需要满足最大航程、最大转弯角、最小航迹段等约束条件。其中,转弯角α 为算法的动作,其最大转弯角约束已在动作空间的设计中加以限定。由于UAV在长距离飞行中,多数时间处于匀速巡航状态,本文设定UAV 的飞行速度V 大小恒定不变。
由于飞行器机动性能的限制和惯性的影响,UAV 在飞行过程中不能随意进行转弯或连续转弯,在改变飞行状态之前必须完成一定距离的航迹段飞行,其大小为无人机当前速度下飞行Δt 时间的距离。如式(18)所示,当V 一定时,li的大小由Δt决定,设Δt=1。因此,UAV 每步的航迹段li的长度大小都相等,设定为固定值1 个单位。
3.2 最大航程相关参数
由于UAV 自身携带能源有限,且相应任务的时间配给有限,其航程必然受限。因此,UAV 的最大航程应当满足式(19)。
其中,Smax表示UAV 燃油限制的最大航程;tmax表示完成任务的最长时间限制。
3.3 深度强化学习参数
本文使用基于PyTorch 搭建的强化学习算法进行训练优化和测试,其算法的参数设置如表1 所示。
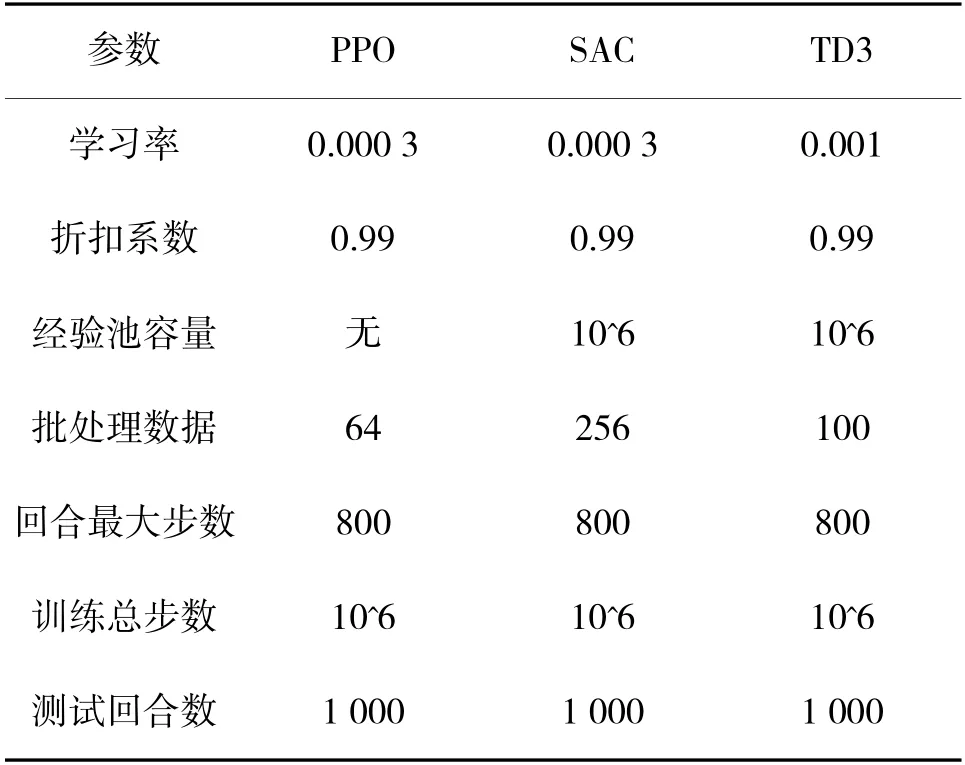
表1 深度强化学习算法参数表Table 1 Parameter list of deep reinforcement learning algorithms
4 实验与分析
4.1 实验环境设计
为验证改进后算法的可行性,本文通过OpenAI的Gym 生成实验环境,共设有两个分步训练环境,1个测试环境,使用PPO 算法、TD3 算法和SAC 算法分别进行优化和比较。
4.1.1 训练环境
第1 个训练环境是300×300 的正方形空白封闭区域,环境边缘均设置为不可触碰的障碍物,正方形内部无障碍物,可由agent 自由通行,仅有一个半径为5 的圆形目标区域,目标的圆心位置和agent的起始位置是在每回合随机设置的,如图6(a)所示。该环境训练的目的是使agent 学会找到通往目标区域的最短路径。
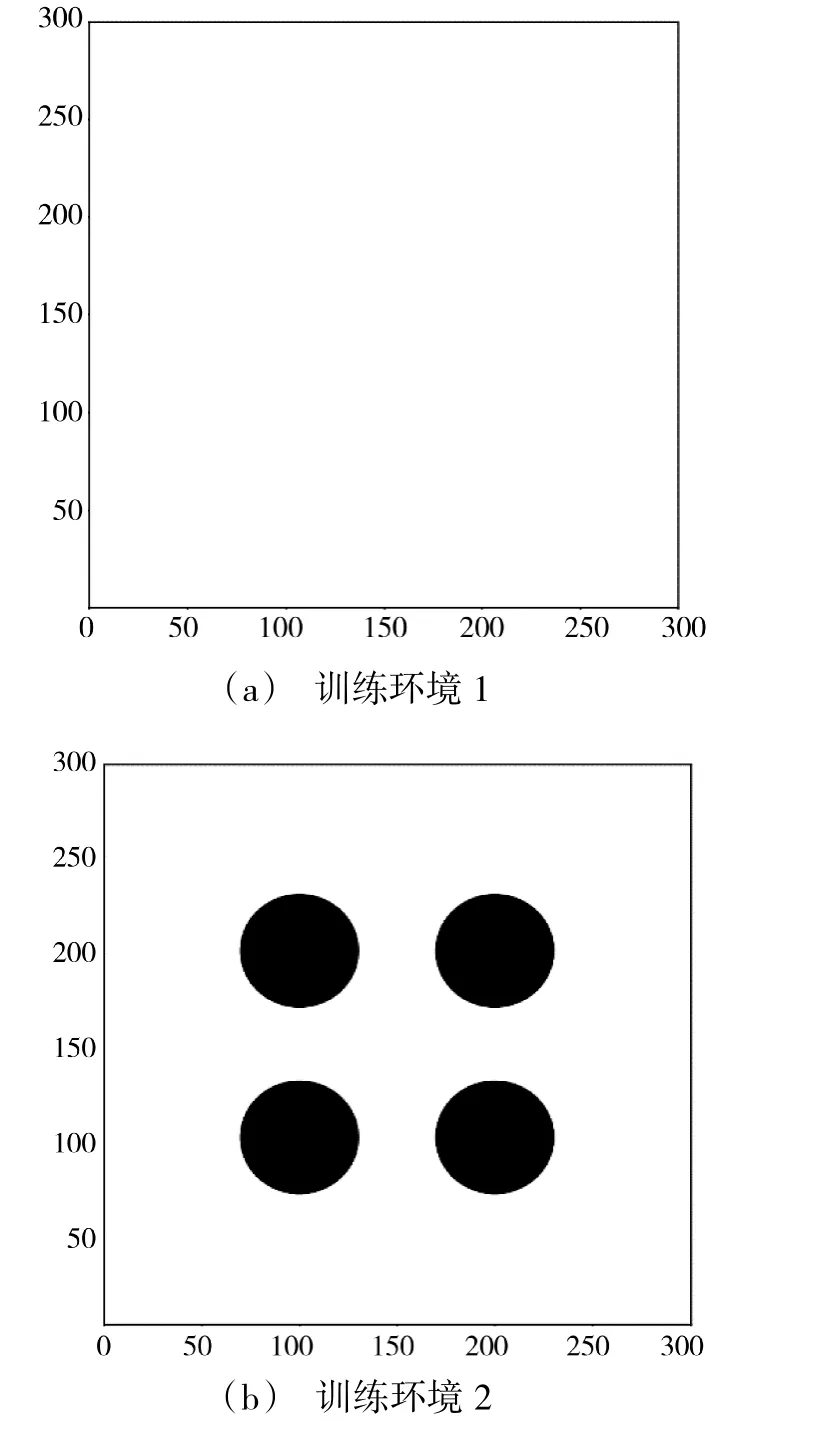
图6 训练环境Fig.6 Training environment
第2 个训练环境是300×300 的正方形封闭区域,环境边缘同样设置为不可触碰的障碍物,内设4个半径为30 的圆形障碍物,1 个半径为5 的圆形目标。其中,4 个圆形障碍物的位置分别为(100,100),(100,200),(200,200),(200,100),圆形目标的位置每回合随机设置,如图6(b)所示。agent 在第1 个环境训练的基础上,再进行第2 个环境的训练,该环境中的学习任务比第1 个环境中学习任务更难,agent 最终学会正确躲避障碍物并找到安全通向目标点的最短路径。
4.1.2 测试环境
如下页图7 所示,测试环境中共设有4 个圆形的障碍物和1 个圆形目标,其分布状况与训练环境不同,但形状大小相同,以验证训练后算法的泛化性和可行性。其中,障碍物的圆心位置分别为(80,80),(220,220),(115,175),(175,115),目标的圆心位置为(280,280)。

图7 测试环境Fig.7 Test environment
4.2 指标构建
4.2.1 训练实验指标
在深度强化学习的训练过程中,主要通过绘制训练过程的成功率和总奖励值曲线,来比较算法收敛速度的快慢、收敛稳定性的好坏、成功率的高低以及总奖励值的大小。由于强化学习算法在状态下进行的动作探索具有不确定性,导致奖励值曲线的噪声较大,不利于进行分析比较,需要进行滤波处理。但若滤波处理过度,则会丢失曲线原有的细节信息,不易分析曲线之间的差异。因此,在本文的训练实验中以50 步为单位,对训练效果曲线采用滑动平均(moving average)的方法进行平滑处理,输出最后的训练曲线图并进行比较。
4.2.2 测试实验指标
将各算法训练加载训练完成的模型,代入测试环境中进行实验。本实验中分别对PPO 算法、SAC算法和TD3 算法进行1 000 回合测试,并统计各算法在测试环境中的测试结果。对每组测试实验设置5 个实验统计指标,分别为:平均成功率、平均奖励值、平均路径平滑度、平均航迹长度以及平均规划用时。各指标的计算方法如下所示:
1)平均成功率
平均成功率是衡量算法泛化性和稳定性的关键指标,算法在陌生环境中收敛的平均成功率越高,算法的可靠性越好,泛化性也更好,反之则更差。指标的计算方法如式(20)所示:
其中,N 为实验总次数;Ns为实验成功次数。
2)平均奖励值
此处以agent 成功完成任务的回合所获得的平均奖励来评判算法优化航迹的好坏,奖励值越高,航迹理论上更优,反之越差。该指标计算公式如下:
3)平均路径平滑度
UAV 进行机动的次数越少,每次转弯的角度越小,对飞行器飞行控制系统的要求就越低,规划出的航迹相对会更平滑,航迹就更优秀。因此,在成功完成任务的前提下,该指标值小的算法更优秀。该指标为agent 任务成功回合的转弯角绝对值之和的平均值,可由式(22)计算得出。
其中,ai为成功回合中agent 每步的转弯角;n 为该回合动作的次数,即该回合的步数。
4)平均航迹长度
由于本文中设定UAV 的飞行速度大小恒定不变且每步的时间间隔相同,UAV 在每步的航迹段长度是相等的,即航迹长度与该回合内步数的大小成正比。因此,以成功回合的平均步数为指标衡量测试过程中UAV 的平均航迹长度。该指标的计算方法如式(23)所示:
其中,Ss为成功回合中UAV 从起点到目标所经历的步数。
5)平均规划用时
由于任务失败回合的规划用时与任务成功回合往往相差较大,为衡量该算法在规划成功时的计算速度,该指标仅计算任务成功时每条飞行轨迹的平均规划用时,以检验算法的实时性。
其中,Ts为成功回合的算法规划用时。
4.3 训练实验
在训练实验中,agent 在每个训练环境中各训练100 万步。环境会根据agent 每步动作的好坏给予一个较小的奖励值。当agent 遇到以下情形时,表示完成一个回合(episode):1)到达目标,当agent 在最大步数内到达目标区域范围内时,表示成功完成任务;2)超出航程,当agent 的运行步数超出最大步数限制时,表示超出UAV 的最大航程,任务失败;3)发生碰撞,当agent 与环境边界或预设障碍物发生触碰时,UAV 因碰撞坠毁,任务失败。每个回合结束时,若完成任务,则给较大的正向奖励,若任务失败,则给予较大惩罚。
从下页图8(a)和图8(b)中可以看出,在训练环境1 中,PPO、SAC 和TD3 算法都能很快收敛,稳定性较好,且收敛得到的奖励值和成功率差别不大,证明3 种算法都能在空旷环境中较好地完成寻的任务。但相对而言,SAC 算法收敛的稳定性更好,速度都更快,曲线最为平坦,优化效果明显更好。
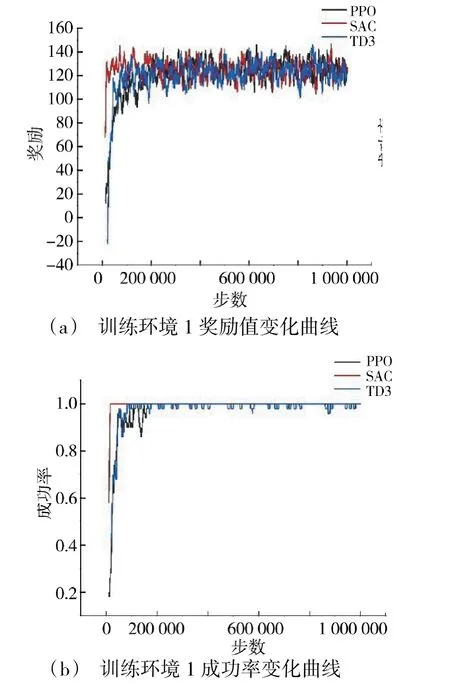
图8 训练环境1 指标变化曲线图Fig.8 Curves of indicator changes in the training environment I
但在训练环境2 中,SAC 算法的收敛速度和稳定性更明显优于PPO 算法和TD3 算法,在10 万步之内就能达到较好的收敛效果,曲线波动非常小。PPO 算法的训练效果最差,从图9(a)和图9(b)中可以看出,由于训练环境2 中的任务过于复杂,PPO算法没有训练形成一个有效模型,训练前后成功率和奖励值无明显变化。TD3 算法的收敛速度比SAC算法慢,约20 万步才能达到收敛效果,且收敛稳定性不如SAC 算法,得到的奖励值与成功率都比SAC算法低。通过训练实验可以看出,PPO 算法比较适合于简单的训练任务,对于复杂任务的训练效果较差;TD3 也有不错的效果,但依然不如SAC 算法;SAC 算法的训练效果最好,能较好完成复杂环境条件下的在线航迹规划任务。
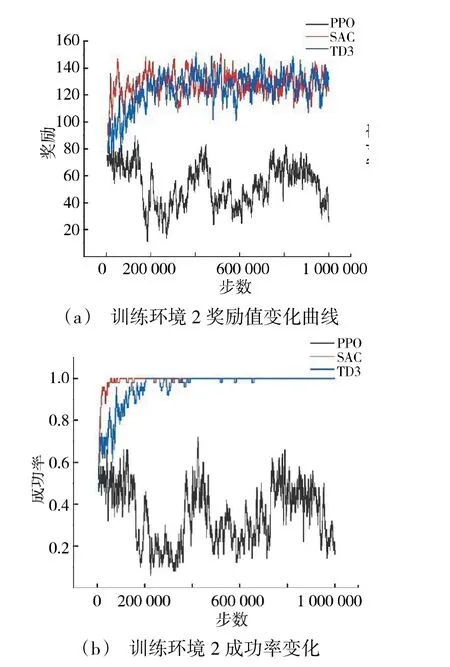
图9 训练环境2 指标变化曲线图Fig.9 Curves of Indicator changes in the training environment II
4.4 测试实验
测试环境中各算法的优化结果如表2 所示,UAV 航迹图如图10(a)、图10(b)所示。PPO 算法在测试环境中无法完成该任务,SAC 算法和TD3 算法能够完成,两种算法的成功率都为100%,能较好地完成该任务,但SAC 算法规划出的航迹更为平滑,机动幅度更小。同样可以看出,SAC 算法得到的航迹更平滑,且规划的航径距离障碍物更远而相对更安全。两种算法单条航迹的计算速度平均值相差无几,证明两种算法的计算速度相当且都能满足UAV的在线航迹规划的实时性需求。通过测试实验可知,SAC 算法得到的航迹更优。
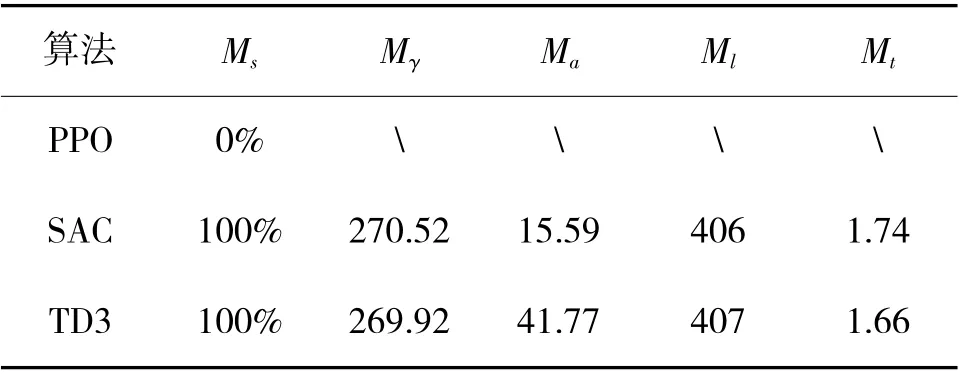
表2 测试实验各指标数据对比Table 2 Comparison of the data of each index of the test experiment
从训练实验和测试实验的结果中可以看出,SAC 算法在处理陌生复杂环境条件下的航迹规划问题时,在收敛性和泛化性方面都具有更强的能力,能满足在线航迹规划的实时性需求。
5 结论
本文根据UAV 导航任务实时性强的特点,设计连续奖励函数对深度强化学习算法进行改进,解决了强化学习算法奖励稀疏的问题。并利用课程学习对复杂实验任务进行分解,降低了任务的学习难度。对比PPO 算法、SAC 和TD3 算法的实验结果可知,SAC 算法的收敛速度更快,具有更好的路径平滑效果,在解决该类问题时更具有优越性。但算法实时性还不够好,下一步可以结合其他算法对状态空间和奖励函数进行改进,加快算法的计算速度。
