工业机器人标定技术分析与研究

陈天炎，韩泽明

（1.福建船政交通职业学院 轨道交通学院，福建 福州 350007；2.福建理工大学 交通工程学院，福建 福州 350108）

定位精度是影响工业机器人性能的重要因素，人们需要经常对工业机器人进行标定，以提高机器人的定位精度来满足工业生产上的需要.但是由于机器人零部件的加工制造误差、装配误差、关节磨损和传动误差等的影响，机器人的绝对定位精度较低，限制了机器人在高精度领域的应用幅度与深度.因此，对工业机器人的绝对定位精度做进一步的研究，具有极为关键的现实价值与意义.

机器人在运动过程中工具中心点（TCP）的位置和姿态是通过运动学数学模型严密计算得到的，运动学模型中含有机器人所有连杆结构尺寸和关节运动参数，这些参数的计算取值与机器人实际参数值之间存在误差，导致计算结果与实际位姿二者之间存在一定的误差.现阶段在实践层面上有如下两种方法用于实现对末端绝对定位精度的提升.1）借助高精度加工设备，并加强与先进装配的配合，据此规避与降低机器人出厂时的内部误差；2）应用更优量的测量工具和方法，对机器人的结构参数进行辨识、分析与校正，此种方法为机器人标定方法[1].从成本出发，第二种方法实现与普及的成本更为低廉；实际效果上，机器人标定方法可以更好地补偿与补救由于机器人的磨损或者结构变形等情况引致的精度降低情况[2].综合来看，现阶段应用机器人标定方法具有更强的可行性，也是现阶段学术界的主要研究内容与方向[3-4].

Judd 等[5]在对机器人标定方法的研究中发现，绝对定位误差的主要原因在于机器人运动学模型在参数上出现了误差传导.因此，现阶段有关于机器人标定技术的研究重点在于辨识机器人运动学参数的误差[6-7].需要指出的是，当前关于运动学参数误差造成机器人绝对定位精度降低的研究中，通常是假定机器人基坐标系和法兰坐标系是已知或者是可以直接测量的.实践中绝大部分的机器人法兰坐标系和机器人基坐标系是“隐藏”的，无法直接测量得到，需要通过特殊的测量和计算方法才能获得[8].文献[9]使用FARO ARM 测量臂对机器人进行标定，使用四元素法获取机器人基坐标系.文献[10]用激光跟踪仪对机器人进行标定，针对IRB2400机器人特定的结构，控制轴1和轴2旋转，以及测量底座平面来确定机器人基坐标系，使用激光跟踪仪配套软件实现坐标变换.在现有机器人标定测量过程中，基本都忽略测量得到的机器人基坐标系和法兰坐标系的位姿误差，而这也是机器人位姿误差模型的重要组成部分，应当在机器人标定过程中给予一并考虑.

机器人位置误差模型或位姿误差模型均可实现对机器人的标定.由于大部分测量设备都能实现对机器人末端位置的测量，相对而言位置误差模型适用的测量设备更加广泛（如三坐标测量机、6或7轴测量臂、激光跟踪仪（配靶球即可）），更具备通用性.为提升机器人的绝对定位精度，针对如下两种误差：1）机器人隐藏的法兰坐标系和机器人基坐标系的测量误差；2）机器人运动学模型参数误差.将这两种误差予以统一，将其确定为绝对定位误差来源，并且基于此进行建模，提出一种相对通用的测量方法，给出参数误差辨识与补偿算法.

1 机器人标定建模

1.1 机器人运动学建模

Denavit等[11]于1955年推出的一种具有较好通用性与普适性的4参数DH模型，是目前使用最广的机器人运动学模型.在实际应用中发现，存在于轴关节之上的某种微小偏差极有可能在DH模型之上反映为一种数值畸变，这也可以理解为参数数值不连续.针对这一问题，Hayati[12]提出了修正后的MDH模型，通过在y轴上增添了一项旋转参数改善模型表现，使得原有的4参数模型，变为5参数模型.即

式（1）中：θi、di、ai、αi分别表示连杆i的关节转角、关节偏置、连杆长度、连杆扭角.关节βi仅存在相邻轴平行的情况下，其他的情况直接将βi=0带入式(1).

根据式(1)可以得到一般N自由度机器人的运动学模型.即

机器人标定一般要借助各种有效的测量手段与方式，尽可能地获取在其基坐标系下的机器人末端的位姿误差.实际机器人末端法兰坐标系和基坐标系是隐藏的，需要构建与测量结果直接相关的测量坐标系.因此，将测量仪的实际测量位置定义为检测中心点（DCP），并且将DCP 确定为构建坐标的原点，据此来构建研究所需要的测量坐标系.因此在对机器人末端位姿进行测量时，需要得到机器人DCP 坐标系相对于法兰坐标系出现的位置变换情况、机器人基坐标系相对于测量仪坐标系出现的位置变换，从而得到DCP 坐标系在测量仪坐标系下的位姿模型，如图1 所示.标定的首要步骤就在于构建DCP 坐标系的位置模型.

图1 DCP坐标系位置模型

1.2 机器人法兰坐标系标定模型

构建模型的关键在于基于测量辨识与获得机器人末端的实际位姿误差，但机器人末端法兰坐标系一般情况下是“隐藏”的，无法直接通过测量设备测量得到.使用测量设备实际测量的位置相对于法兰坐标系存在一定偏移量（如图2所示）.

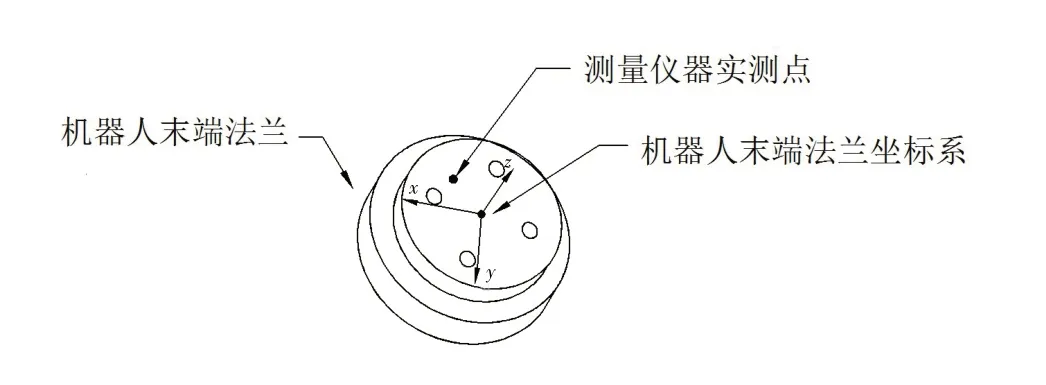
图2 实际测量点与法兰坐标系

式中：D表示DCP;L表示测量仪器实测点DCP.

假设机器人在某个状态下法兰坐标系位置为O，控制机器人末端位置不变，只改变姿态，通过对多个点进行测量，即可以借助于对球心的拟合，据此可以获取O点位置坐标.从理论层面分析，拟合空间之中的4 个非共面点，就可以获取球心坐标.因此，首先假设球心坐标为(a,b,c)，半径为R，并且将这4 个测量点的坐标设定为(x1,y1,z1)(x2,y2,z2)(x3,y3,z3)(x4,y4,z4).据此得到方程组为

通过求解式(4)得到法兰坐标系的原点位置，后续需要进一步导出法兰坐标系姿态.若可以确保机器人控制器在TCP 坐标系下，其运动方向是沿着确定的法兰坐标系的x，y，z三轴.那么就可以在控制器每一次的运动进程之中，提取出2 个以上的点，由此来表述并确定其坐标轴方向，然后获取法兰坐标系的x，y，z轴在测量仪坐标系下的矢量n,o,a，并且最终得到位姿矩阵，即

据此可以计算得到由机器人末端法兰坐标系到设定的DCP点之间的位姿变换，即

1.3 机器人基坐标系标定模型

从实践层面分析，在实际测量机器人末端位姿的过程中，所获取到的数据是较之于测量仪器自身所处的坐标系来进行讨论的.因此，为确保所获取到的实际位姿与名义位姿具有可比性，需要将二者统一至同一个坐标系之中.

具体来看，可以将机器人末端法兰坐标系名义位置和姿态用PN和RN来呈现，测量仪测量得到的某点的实际位姿用PC来表示.并且将前提条件设定为不考虑DCP坐标系姿态，基于此，可以基于空间几何变换，得到下述的变换关系

式中：T、R分别表示测量仪坐标系到机器人基坐标系的旋转变换和平移变换；E表示3×3的单位矩阵；PL为法兰坐标系到DCP点的位置变换，上标N为“Nominal”缩写，表示名义值（下同）.

式(9)中，共计有12个未知数，因此，需要获取到最少4个点的位置.实际上，为了减少误差所使用的位置数远多于4组，这就使得式(9)成为了超定方程组.令

则超定方程组用矩阵可表示为

式中：A为TNL元素组成的系数矩阵；B为测量值PC组成的矩阵.

应用最小二乘法来对式(11)进行求解，得

据此可以得到测量仪坐标系与机器人基坐标系之间的变换关系X.这样可以将测量到的末端位姿和控制器中显示的末端位姿予以统一.

2 DCP位置误差模型

在计算机器人基坐标系时使用的机器人末端位置是直接从示教器中读取的，这与机器人实际位置存在偏差，因此计算所得的机器人基坐标系相对于测量仪坐标系的位置也存在偏差.同样，在测量和计算DCP 位置时，由于测量扰动的影响，计算得到的DCP 位置也存在一定的误差.将通过模型计算得到的DCP 位置和机器人基坐标系位置分别定义为名义DCP 和名义基坐标系，如图3 所示.DCP的名义位置与实际位置产生一定误差的影响要素主要有运动学参数误差、基坐标系位置误差，以及DCP坐标系位置误差.

2.1 机器人运动学参数误差

实践中，由于机器人的磨损变形是绝对存在的，因此各连杆参数始终存在误差，使得运动学模型参数在名义值和实际值上也将出现偏差.整体来说，影响到机器人末端位姿的参数误差主要有

其中：Δβi仅在相邻轴呈现平行状态.如若不然，则确定Δβi=0.

此外，可以将机器人基坐标系到末端法兰坐标系之间的实际变换关系表述如下

式中：R表示Rot，旋转变换；T表示Trans，平移变换.

2.2 机器人基坐标系参数误差

机器人基坐标系误差可以基于式(13)计算得到的名义位姿矩阵呈现，即

式(14)中用来呈现姿态与位置的参数共计有12个，为了降低需要辨识与测量的参数数量，将其改写为一个平移变换和三个旋转变换组合成的一个6参数模型，即

机器人基坐标系的参数误差就可以表述为[Δxc,Δyc,Δzc,Δθxc,Δθyc,Δθzc].

式中：上标R为“Real”缩写，表示实际值.

2.3 DCP坐标系参数误差

假定机器人DCP坐标系相对于机器人末端法兰坐标系的位姿变换矩阵为，并参考前文中机器人基坐标系误差的推导方法，可以获取到机器人末端法兰坐标系跟DCP 实际坐标系二者之间的变换模型，即

并且在确定了3个位姿模型的基础之上，将其进一步整合，可以构建在测量仪坐标系下的DCP实际位姿模型，将这一变换矩阵表述如下

式中：R表示DCP坐标系在测量仪坐标系下呈现的姿态；P则代表的是DCP坐标系在测量仪坐标系下呈现的位置.

DCP的实际位姿可以表示为

影响DCP位姿精度的参数误差为

位置误差模型相对而言更具备通用性，因此忽略DCP姿态误差，设参数误差集合为Δq，结合式(19)，DCP的实际位置模型可以表示为

据此，可以将DCP位置误差与模型之中的各参数误差之间所具有的数学关系表述为

式(21)中位姿误差和各参数误差呈非线性关系，直接求解难度较大.从偏微分角度分析，对于含有n个参数误差的模型，式(21)可以写成

式(22)可以简化为

式中：ε表示DCP位置误差；Δq表示标定模型所有的参数误差；M表示误差系数矩阵.

3 参数误差辨识及补偿

3.1 冗余性参数分析

文件得到了机器人DCP 位置误差模型：ε=MΔq.其中ε可以测量获取，而M代表的是误差系数矩阵，M是经由误差模型进行推导得到，Δq是需要求解的参数误差.由此可知，为获取参数误差的解，仅需要将ε代入至DCP 位置误差模型中，计算Δq.但是考虑到实践中不可避免地存在机器人运动学参数冗余，对Δq的求解准确性与精度产生直接影响.因此，设定代表机器人连杆坐标系{i}到连杆坐标系{i+1}的齐次变换，在只考虑位姿变换时，可以把β≈0直接带入式(1)，得到

根据机器人微分运动学，结合式(23)可以得到连杆坐标系{i}和连杆坐标系{i+1}之间的微分变换关系[14]，即

假设机器人的自由度数为N，将式（26）的两边均乘以，确保两个坐标系之中的微分误差都可以实现向机器人末端的转换.由此可得

由式(27)可知，连杆坐标系{i}的微分误差dzi和δzi对末端造成的影响可以由连杆坐标系{i+1}的微分误差来呈现.这说明连杆坐标系{i}与连杆坐标系{i+1}各自的微分误差dzi和δzi具有相关性，存在冗余性.将测量仪坐标系到机器人基坐标系的变换模型参数中dz和δz确定为冗余参数.则有

观察式(28)可知，Gi中变量只有a和α.针对a和α取不同值，得到表1.

表1 机器人运动学参数冗余性辨识

3.2 参数辨识算法

如前文所述，机器人DCP 的位置及姿态的微分误差模型表述为

去掉Δq中的冗余性参数，可以辨识参数的数目N，由此可以确定，Mp、Mδ均为3×N的系数矩阵.实践中，为了规避误差对求解精度的干扰，需要借助大量的数据对模型进行拟合.具体来看，设定实践中共计测量得到K组(K>N/3)机器人位置数据，可以获取到方程组为

式(30)是一个超定方程组，可以使用最小二乘法求解，由此可得

式中：M+表示系数矩阵M的广义逆.

3.3 参数误差补偿算法

大部分机器人控制器生产厂家不会对修改权限授权，仅可以调整关节角度θ.处于不同位姿的机器人，其运动学参数d、a、α、β的误差，各自对机器人的位姿误差具有差异化的影响.因此，使用牛顿迭代法逐步调整各关节的角度θ，从而实现对运动学参数误差导致的机器人末端的位姿偏差的补偿.假设机器人目标位姿为TN，将Δdi,Δai,Δαi,Δβi代入模型求得TR,再将名义位置与实际位姿的差对各关节角求偏导，可得

由式（32）可求得各关节实际转角，再通过关节实际转角求得应该给定的指令位置，使机器人达到实际位置.

4 结束语

为促进机器人产业的发展，扩大机器人在高精度领域的应用，对机器人精度的提升方法进行研究.首先从实际测量角度出发，建立DCP 坐标系，并给出相对通用的DCP 坐标系和机器人基坐标系的测量方法，建立完整的误差模型；然后利用微分运动学建立微分误差模型，得到误差辨识方程，并且具体分析误差模型之中存在的冗余性参数误差，明确提出对冗余性参数误差进行辨识的可行方法；最后提出了对参数误差进行补偿的具体方法.研究工作对机器人工作精度提升有一定的研究意义.