H2S和H2S+的振动光谱和电子能谱计算

郭 甜,徐建刚,张佳美,张思雨,陈艳南,张云光

(西安邮电大学 理学院,西安 710121)

1 引 言

H2S分子的物理和化学性质在星际介质大气中起着重要的作用，它的微波和红外光谱在许多振动状态下显示出不寻常的谱带强度[1].例如，H2S的基频振动比类似的三原子分子(如H2O和H2Se)弱两到三个数量级，不仅如此，它的组合频ν1+ν2、ν2+ν3和ν1+ν3也比类似分子弱得多[2，3].

它还是一种轻质、非刚性的不对称转子分子，引起了众多学者的关注.1975年cook等人对H2S旋转光谱的微波研究，提供了精确的旋转常数和四次畸变常数[4].1990年，Kauppi和Halonen运用微扰理论计算了硫化氢分子的势能面[5]，并用非线性最小二乘法优化了势能参数.之后，Polyansky提出对运动动能算符的非绝热修正[6].Kozin和Jensen通过拟合高分辨率光谱学实验中观察到的随机能级[7]，使用莫尔斯振子刚性弯曲内部动力学代码优化了势能面.Martin于1995年通过从头计算得到了电子基态的H2S势能面[8].Xie等人采用VSCF-CI方法计算了H2S的高激发振动态的能量[9].Cazzoli等人获得了硫化氢的两种同位素的旋转光谱[10].Lodi等人计算了H2S分子从头算偶极矩面，发现核心修正和相对论修正对谱线强度有显著贡献[1].Carvajal等人提出了一种基于非谐阶梯算子分析分子振动结构的新模型，并将其应用于H232S分子[11].

H2S由于其自身性质引发了人们对其更深层次的研究兴趣；另一方面，电子状态可以用于确定不同分子性质的光离过程，如电离能或结构参数，用于识别分子UV/VIS的电子激发或具有特征跃迁的荧光过程，如有机发光二极管.已有较为强大的实验技术来测量和研究这些转变.对理论方面而言，简单绝热跃迁的计算较为容易，但这些计算不能描述包含重要信息的光谱的精细结构[12].对分子光电子能谱不同跃迁的光谱带的计算和分配变得越来越重要，振动贡献或垂直激励等性质可以用Franck-Condon factors (FCFs)来解释[13，14].因此，本文计算了H2S及H2S+势能面及振动光谱，并基于初态(H2S Χ1A1)和末态(H2S+X2B1)势能数据绘制相应光电子能谱.

2 理论计算

本文所有计算在MOLPRO 2018量子化学软件包中C2V点群下进行，以Hartree-Fock (HF)方程为起点，对H2S和H2S+分子轨道进行初始猜测，采用(非限制)单双耦合簇理论[(U)CCSD]结合相关一致基组cc-pVQZ对H2S和H2S+优化几何结构，使用同一层次理论计算了分子振动产生的谐振频率及一维、二维势能面，势能面使用多模展开，并在3D项之后截断.

(1)

(2)

(3)

(4)

势能面V(q)沿法坐标q展开，V0表示平衡结构的总能量，高阶耦合项是对低阶贡献的修正.一旦势能面确定，就可以通过求解薛定谔方程来确定振动波函数，沃森哈密顿的振动自洽场理论(VSCF)被用于确定并优化初始猜测得到的单模波函数，在这些初始计算中使用了20个分布式高斯基.

(5)

在后续的计算中，使用Culot和Lievin提出的VMCSCF方法[15]修正静态相关效应，并将VCI系数冻结，使用一个向量进行VMRCI[16]计算修正动态相关效应，得到H2S和H2S+的基频、倍频以及组合频.最后使用拉曼波函数(RWF)方法和收缩不变Krylov子空间(CIKS)中基于残差的特征对计算算法(RACE)[17，18]模拟了H2S Χ1A1→H2S+X2B1的光电子能谱.

3 结果与讨论

3.1 H2S及H2S+的空间几何结构

H2S与水分子相似，在C2V点群下共享一组共同的对称适应分子轨道.也就是说，中心原子S的原子轨道与H2的1σ轨道的对称和反对称组合相互作用.表1列出了在(U)CCSD/cc-pVQZ理论水平下优化得到的H2S、H2S+几何结构参数.与实验值的相比，本次计算得到H2S中S-H的键长略微高于实验值，仅相差0.0006 Å，θHSH键角偏离约0.5°，一致性良好.相比H2S，H2S+中的S-H键长和θHSH键角分别扩展至1.3564 Å，93.3624°，当H2S阳离子达到平衡状态时，键长和角度分别增加了约1.5%和1%.此外，由于H2S+的平衡几何结构参数实验值的缺乏，我们还提供了其他学者的计算结果以供对比，S-H键长相差0.00032 Å，键角偏离约0.28°.

表1 H2S及H2S+的平衡几何参数

3.2 势能面

3.2.1一维势能面

图1中上图和下图分别为面内弯曲振动和S-H键对称拉伸振动产生的一维非对称势能曲线，而S-H键的非对称拉伸振动产生了对称势能曲线，如图2所示；当分子振动模式所代表的对称性不可约表示不同于A1时，会产生对称势能曲线.在能量大小的变化上，能明显看出S-H键的拉伸振动对分子势能影响较大，是面内弯曲振动的2倍至3倍；而S-H键的非对称拉伸振动对分子势能变化的影响最大.在对称势能曲线产生的过程中，使用分子对称性还会使加快计算速度，使CPU时间减少一倍.

图1 H2S振动产生的非对称势能曲线

图2 H2S振动产生的对称势能曲线

3.2.2二维相对势能面

H2S三个基频振动模式两两组合共可以产生三个二维势能面，势能面的展开采用法线坐标，横坐标数值的大小和正负代表分子处于振动状态时各原子空间位置的变化，每个二维势能面沿法坐标方向生成16(24)个网格点.由于零势能处的选取，使得纵坐标势能产生了负值，让分子在振动时的能量变化更为明显，并且在两个横向坐标同时达到最大值时变化最大.在图3中的二维相对势能面中，仍能明显看出在横坐标对称性不同于A1时，所在横轴沿坐标轴方向延伸的势能变化表现出对称性，如图3中(b)和(c)中横坐标方向的q3.

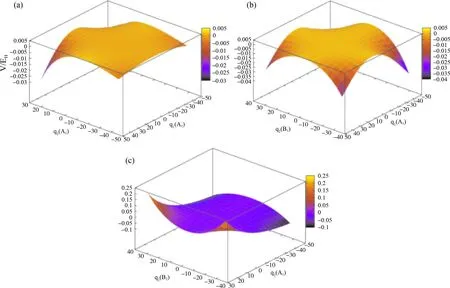
图3 H2S振动产生的二维相对势能面

3.2.3二维完整势能面

三模耦合项用电子密度碎片化来模拟，它包含了对势能的1D贡献.使用参考几何RGHF方法对多维势能面展开中高阶项进行建模，该方法基于平衡结构的局域电子密度，其关键步骤是在给定的参考结构下，将电子密度定位到分子的原子上，然后将这些原子中心的部分密度转移到扭曲结构的原子位置.图4展示了H2S振动产生的二维完整势能面，其中，(a)为沿S-H键对称拉伸振动(q2)和H-S-H面内弯曲模式(q1)法线坐标展开的2D势能面的特征，仅在横坐标同时为0时分子处于能量最低状态，S-H键对称拉伸振动较H-S-H面内弯曲振动分子能量变化更为明显；图4(c)中的势能变化特征类似.而对图4(b)而言，S-H非对称伸缩模式(q3)和H-S-H面内弯曲模式(q2)振动模式共同作用使得纵坐标分子能量变化范围明显变大，且分子势能在q3横坐标正向和负向最大时达到最大值，也就是说，此时分子振动最为剧烈.

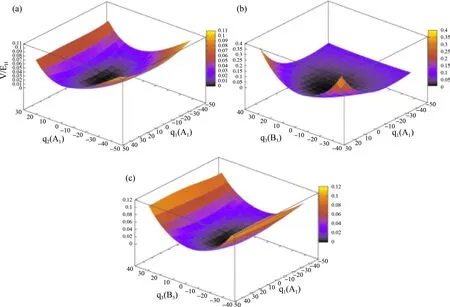
图4 H2S振动产生的二维完整势能面

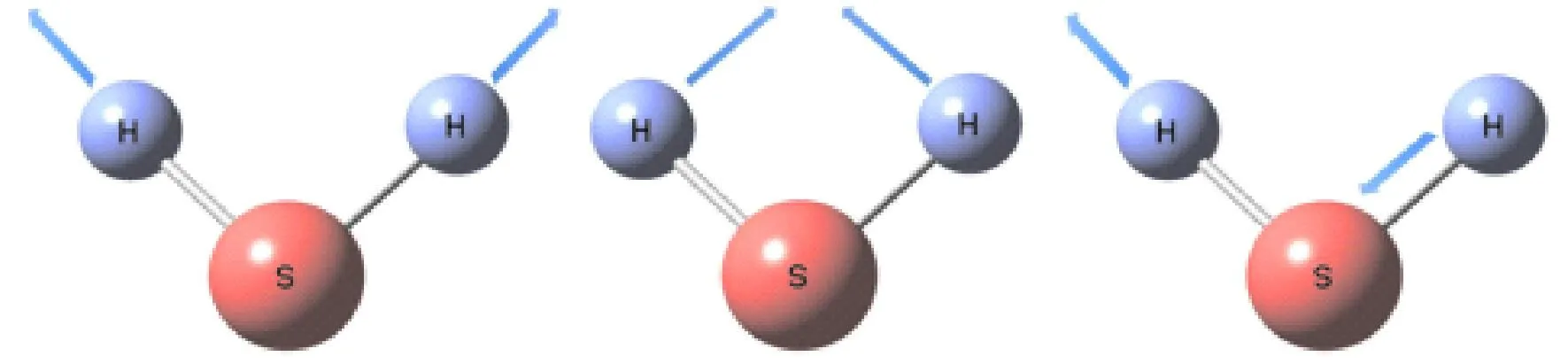
图5 H2S的基频振动模式

在势能面的计算中，对称性可以被用在单个表面的构造中以节约时间和资源，在势能变化中，S-H键的拉伸振动对分子体系的能量影响相对较大，并且不同振动模式的耦合对也会影响分子的势能变化，这些依赖于直线法线坐标的多维高级势能面都是通过MOLPRO完全自动生成.

3.3 振动频率

H2S分子三个基频振动模式如图1所示，ν1为S-H键的对称拉伸的振动，ν2为θHSH的面内弯曲振动，ν3为S-H键的非对称拉伸振动.对比计算得到的谐振频率和VSCF修正的结果，可以得出H2S在VSCF计算后对振动模式间非谐效应的对三个振动模式的修正分别为：66.67 cm-1、27.85 cm-1、84.84 cm-1；H2S+在VSCF计算后非谐效应的修正大概为：31.13 cm-1、65.07 cm-1、85.12 cm-1.在不同方法下获得的H2S及H2S+的基频如表2所示.H2S中VMRCI的计算结果与实验结果之间的平均绝对误差约为21.69 cm-1，而VSCF的结果与实验值之间的平均绝对误差约39.81 cm-1，说明引入对相关效应的校正后使得误差减少至二分之一，此外，使用VMRCI引入相关动态效应的校正对S-H键的拉伸振动的结果更为明显.最精确的理论结果和实验数据之间显示出一定的偏差很大程度上是因为在计算中忽略了势能展开中的高阶耦合项，这可能导致基本振动产生约10 cm-1的误差.表3汇总了倍频和组合频的计算结果，经过与有限的实验值对比，一致性较好，此外，表中2ν1和ν1+ν3振动带之间发生耦合，相应带隙小于1 cm-1，从而产生费米共振.对于H2S+而言，失电子使得其与H2S在相同振动模式下时的基频、倍频以及组合频减小，只有在组合频2ν2+2ν3较H2S振动频率增大.

表2 H2S及H2S+的谐振频率和非谐振动频率 (cm-1)

表3 H2S及H2S+的倍频、组合频 (cm-1)

3.4 振动光谱

H2S振动产生的红外光谱中，最明显的吸收峰出现在1195 cm-1处，由θHSH的面内弯曲振动产生，如图6所示；而第二强烈的吸收峰出现在图中的近红外光谱区域，这是由于组合频ν2+ν3(5203.45 cm-1)和倍频2ν1(5203.48 cm-1)之间的耦合，相应能级间的带隙较小(仅相差0.03 cm-1)，产生费米共振，使得为对应波段处的红外吸收强度变大.在2600 cm-1附近有两个吸收峰，高低峰分别由S-H键的非对称和对称拉伸振动产生；2380.37 cm-1处出现吸收峰来源于倍频2ν2.在图7的拉曼光谱中能明显看出三个强度较高的峰值，其中，2600 cm-1附近显示了最强烈的拉曼活性，对比而言，相同频率处红外光谱显示出的吸收峰较为微弱，高低峰同样分别由分子基频振动中S-H键的非对称和对称拉伸振动产生，另外一个峰值出现1195 cm-1处H-S-H键的面内弯曲振动，另有2362.08 cm-1、3871.28 cm-1、5329.40 cm-1处分别出现极为微弱的活性.强度拉曼光谱作为红外光谱的补充，帮助我们更准确地分析分子的振动结构.

图6 H2S的振动产生的红外光谱

图7 H2S分子振动产生的拉曼光谱

3.5 光电子能谱

图8中的(a)和(b)分别为T=300 K时使用RWF和CIKS模拟的H2S Χ1A1→H2S+X2B1光电子能谱.在振动构型基的选择中，最大总激励水平为8，同时激励模式的最大数量为3，单模最大激励水平为8；取近似对应于模态收缩Frank-Condon因子(MCFCFs)分布平均值的模态；根据初始状态的相对基态振动能级做出预筛选，1×10-3以下的初始状态将被忽略.RWF使用基于非齐次薛定谔方程的时间无关本征态无ansatz评估光谱，方程的解与光谱强度直接相关，在Lanczos基下RWF计算的收敛阈值设置为tRWF=2×10-4；CIKS用Lanczos或RACE方法确定具有最大Franck-Condon 因子的本征态，通过RACE方法得到的光电子能谱如图8(b)所示，在该方法下，a实验值来源于文献[21-24]定义了FCF之和的阈值定义为0.99.从图中容易看出，两种方法绘制光电子能谱图总体一致，但RWF方法得到的光谱图更为精细，较CIKS而言出现的峰值更多，在横坐标为11-11.5 eV以及12.5 eV后仍有的微弱峰值，如图8(a)中的放大部分所示.图8(b)中12.2 eV至12.3 eV处有两个峰值，而对应于(a)中的同等位置处有三个峰值，由于峰值个数的增加，再加之图像绘制时高斯函数中半宽大小的设置，致使RWF中相应的峰略微右移.

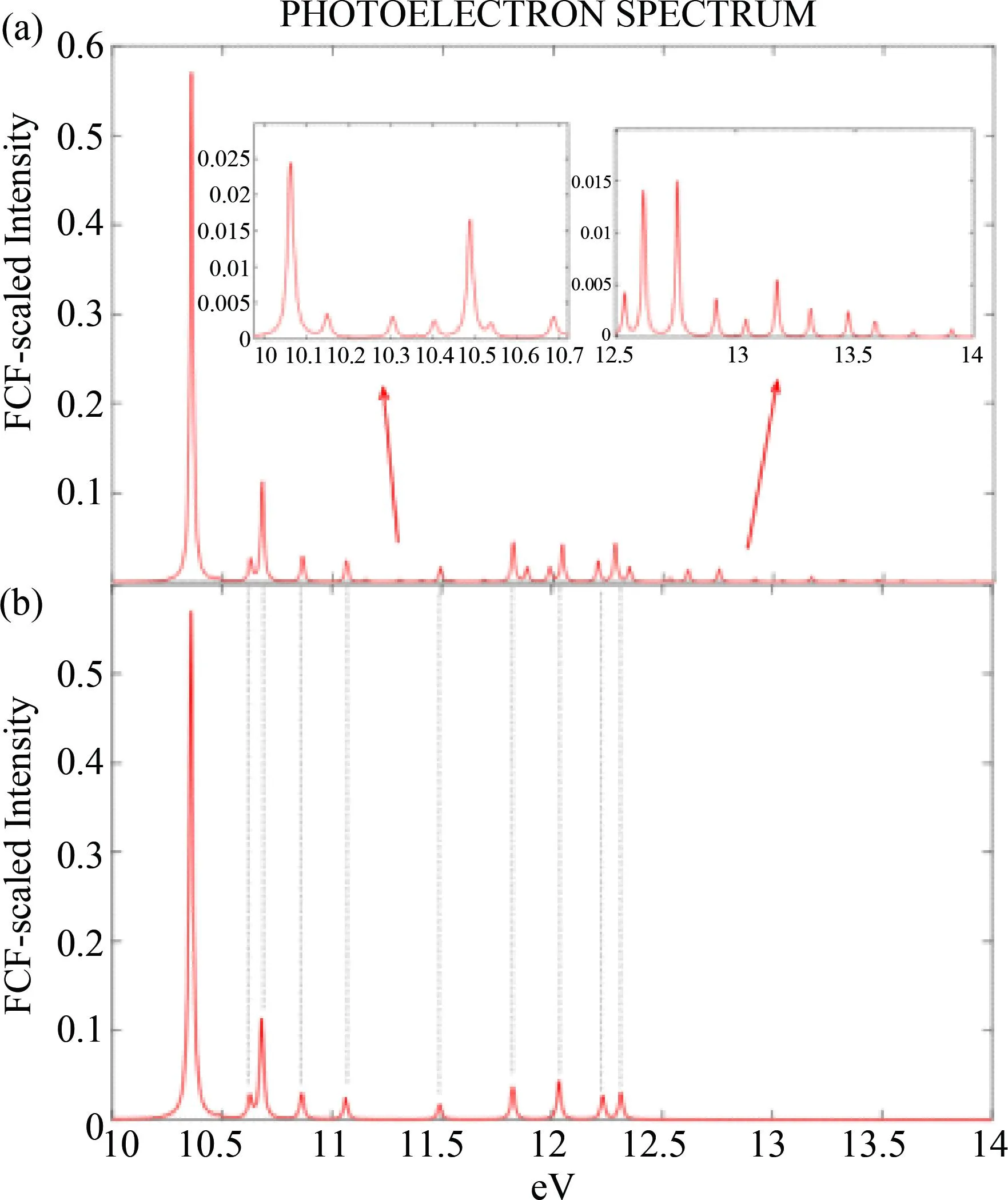
图8 H2S Χ1A1→H2S+ X2B1的光电子能谱

4 结 论

本文基于MOLPRO量子化学程序包，使用从头算方法在(U)CCSD/cc-pVQZ理论水平下计算了H2S以及阳离子H2S+的势能面及光电子能谱.从势能面的特征中可以看出不同振动模式对分子能量变化的影响，S-H键拉伸振动产生的能量为面内弯曲振动的2至3倍，并且S-H键的非对称拉伸振动和面内弯曲振动共同作用会使得势能变化范围明显变大.VMCSCF和VMRCI分别被用来修正静态相关效应和动态相关效应以获取非谐振动频率和振动光谱，结果表明，较H2S而言，失电子使得H2S+在相同模式下的非谐振动频率变小.此外，H2S分子在组合频ν2+ν3(5203.45 cm-1)和倍频2ν1(5203.48 cm-1)处的带隙小于1 cm-1，产生强烈的费米共振，致使红外光谱中相应波段处的吸收强度明显变大，超过个别基频振动产生的吸收峰.最后，基于势能面使用RWF和CIKS方法首次计算了H2S Χ1A1→H2S+X2B1的光电子能谱，两种方法所得电子能谱图像总体一致，但RWF方法所得光电子能谱图像显示出更多的峰值，为其实验研究和星际探测提供理论数据支撑.