动态系统加性干扰与状态估计的实时滤波方法

陈健,文成林

(1.吉林化工学院 信息与控制工程学院,吉林 132022;2.广东石油化工学院 自动化学院,广东 茂名 510006;3.中国科学院深圳先进技术研究院 广东省机器人与智能系统重点实验室,广东 深圳 518055)

随着滤波器的不断发展与改善,滤波器设计和状态估计问题逐渐成为研究的热点之一[1]。实际应用中,最具有代表性的是线性白噪声系统下的卡尔曼滤波,它是基于均方误差最小准则下的递归最优状态估计方法[2,3]。当系统呈现为弱非线性时,一般将非线性系统线性化,转化为符合线性卡尔曼滤波器的标准形式,再进行相应的滤波器设计[4-8]。模型中误差变动的影响,大大增加了模型的不确定性,导致滤波器的性能下降,容易引起滤波的发散[9]。因此,针对模型的不确定而造成的滤波器性能下降,进而引起滤波器性能失效的问题,本文建立了相应的多不确定性下的新型滤波器。本文主要围绕一类线性系统中因建模误差引起模型不确定情况进行研究,首先将不确定因子视为加性干扰[10-12],通过设计出求取状态模型中不确定因子当前值以及未来值的辅助方程,再基于未来观测信息的顺序求出状态模型中不确定因子的当前值和测量模型中不确定因子的未来值,进一步优化求解未来状态中基于测量模型和状态模型在线调整的自适应滤波器[13]。

1 线性系统加性滤波设计方法

1.1 问题陈述

考虑如下随机系统

x(k+1)=A(k)x(k)+D(k)d(k)+w(k)

(1)

y(k+1)=B(k+1)x(k+1)+C(k+1)r(k+1)+v(k+1)

(2)

式中:k为离散时间;A(k)为系统状态转移矩阵;B(k+1)为观测矩阵;D(k)和C(k+1)为系数矩阵;x(k)∈Rn为状态向量;y(k+1)∈Rm为观测向量;d(k)和r(k+1)为系统中的不确定因子。

假设系统建模误差w(k)和v(k+1)为不相关的白噪声序列,满足

E{w(k)}=0,E{v(k)}=0

(3)

E{w(k)wT(j)}=Q(k)δkj,E{v(k)vT(j)}=R(k+1)δkj

(4)

式中:Q(k)为噪声w(k)的方差;R(k+1)为噪声v(k+1)的方差;δkj为Kronecker积。

根据式(1)和式(2)可以看出,状态变量x(k+1)的变化受加性干扰d(k)和r(k+1)的影响。因此,需要利用d(k)和r(k+1)的估计值对状态x(k+1)进行估计。

1.2 加性干扰d(k)的Kalman滤波器设计

观测模型y(k+1)没有关于加性干扰d(k)的显示信息,而d(k)的变化会反映在状态x(k+1)中,因此,以随机游走的形式建立一步滞后的动态模型,可得

d(k)=Ad(k-1)d(k-1)+wd(k-1)

(5)

为了对加性干扰d(k)精确估计,观测模型简化为

y(k+1)=B(k+1)(A(k)x(k)+D(k)d(k)+w(k))+C(k+1)r(k+1)+v(k+1)

(6)

假设如下统计特性

(7)

式中:Ad(k-1)为状态转移矩阵;wd(k-1)为零均值的高斯白噪声;Qd(k-1)为噪声wd(k-1)的方差。

(8)

根据标准卡尔曼滤波器设计原理,加性干扰d(k)的滤波器设计可以分为时间更新和测量更新两个步骤,具体如下。

步骤一:时间更新

通过式(5),得到关于d(k)的预测值和预测误差协方差矩阵

(9)

(10)

步骤二:测量更新

根据式 (6),可得加性干扰d(k)的测量预测值及测量预测误差分别为

(11)

(12)

则d(k)的滤波器设计为

(13)

相应的估计误差为

(14)

结合正交原理得到滤波器中Kd(k)

Kd=Pd(k|k-1)DT(k+1)BT(k+1)[B(k+1)A(k)Px(k|k)AT(k)BT(k+1)

+B(k+1)Q(k)BT(k+1)+C(k+1)Pr(k+1|k)CT(k+1)

+R(k)+B(k+1)D(k)Pd(k|k-1)DT(k)BT(k+1)]-1

(15)

最后,根据式(14)求得估计误差协方差矩阵为

Pd(k|k)=[I-Kd(k)B(k+1)D(k)]Pd(k|k-1)

(16)

至此,状态模型中的加性干扰d(k)的滤波器设计就完成了,改写测量模型,使模型中出现d(k)的显示信息,本质上是原始测量模型的等价改写。

1.3 加性干扰r(k+1)的Kalman滤波器设计

本节的目标是设计观测模型中加性干扰r(k+1)的Kalman滤波器,同样以随机游走的形式建立动态模型即

r(k+1)=Br(k)r(k)+wr(k)

(17)

假设如下统计特性

(18)

式中:Br(k)为状态转移矩阵;wr(k)为零均值的高斯白噪声;Qr(k)为噪声wr(k)的方差。

根据标准卡尔曼滤波器设计原理,加性干扰r(k+1)的滤波器设计过程分两个步骤,具体如下。

步骤一:时间更新

基于r(k+1)的动态模型,得到r(k+1)的预测值及预测误差协方差矩阵

(19)

步骤二:测量更新

根据式(2)求得加性干扰r(k+1)的测量预测值和测量预测误差分别为

(20)

(21)

则r(k+1)的滤波器设计为

(22)

以及相应的估计误差为

(23)

最后,利用正交原理再结合估计误差以及观测模型可得增益矩阵,并根据式(27)得到Pr(k+1|k+1)

Kr(k+1)=P(k+1|k)CT(k+1)[B(k+1)Px(k+1|k)BT(k+1)

+C(k+1)Pr(k+1|k)CT(k+1)+R(k+1)]-1

(24)

(25)

至此,我们完成了状态模型和观测模型中的加性干扰r(k+1)和d(k)的Kalman设计过程。

1.4 求解系统状态变量x(k+1)估计的Kalman滤波器

本节的主要目的是在已获得的加性干扰d(k)和r(k+1)估计值的基础上,基于原始状态模型和测量模型,求解系统状态状态变量x(k+1)的滤波器,即

(26)

根据标准卡尔曼滤波器设计原理,滤波器的设计过程如下。

步骤一:时间更新

根据式(1)可得x(k+1)的状态预测值、状态预测误差及预测估计值误差协方差矩阵,分别为

(27)

(28)

Px(k+1|k)=A(k)Px(k|k)AT(k)+D(k)Pd(k|k)DT(k)+Q(k)

(29)

步骤二:测量更新

根据状态预测值和观测模型可得测量预测值和测量预测误差,分别为

(30)

(31)

则状态变量x(k+1)的滤波器设计为

(32)

以及相应的状态估计误差

(33)

式中:Kx(k+1)为增益矩阵。利用正交原理求解得增益矩阵可得

Kx(k+1)=Px(k+1|k)BT(k+1)[B(k+1)Px(k+1|k)BT(k+1)

+C(k+1)Pr(k+1|k+1)CT(k+1)+R(k+1)]-1

(34)

最后,根据式(33)求期望得到Px(k+1|k+1)

(35)

2 误差分析

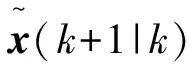
从滤波更新过程中可以看出,加性干扰d(k)和r(k+1)以及状态x(k+1)三者互为影响,对于已经估计出来的变量,在测量方程中显示为k+1的估计值,对于未估计出的变量,显示为预测值,而对比现有的方法统一视为预测值。因此,与STF相比,本文的方法的实时性更好。

3 仿真验证

考虑如下随机系统

x1(k+1)=x1(k)+a1(k)+w1(k),y1(k+1)=x1(k+1)+0.01r1(k+1)+v1(k+1)

x2(k+1)=x2(k)+a2(k)+w2(k),y2(k+1)=x2(k+1)+0.02r2(k+1)+v2(k+1)

(36)

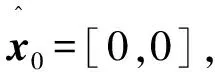
图1～图6为各变量的估计曲线以及各变量的估计误差曲线,由式(15)～式(18)、式(22)～式(29)、式(31)～式(35)得出。表1为各变量的估计误差求和平均后的结果。

图1 状态x的估计值

图3 参数a的估计值

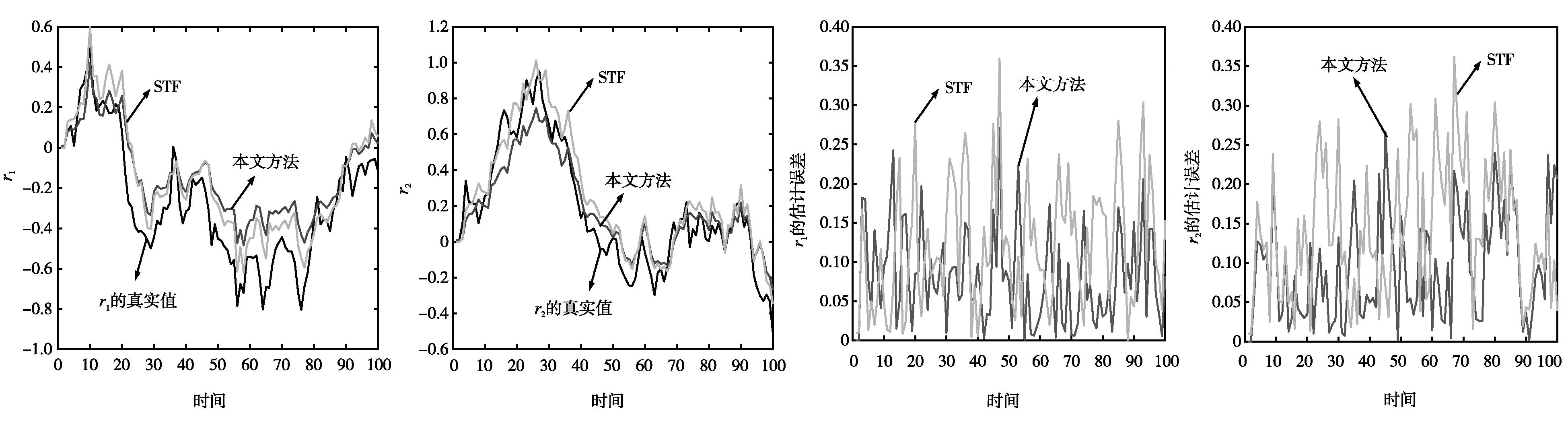
图5 参数r的估计值

表1 估计误差平均值

由图1～图6和表1可看出,对比STF,本文所提出的实时滤波方法具有更好的滤波性能,加性干扰a1(k)、a2(k)、r1(k+1)和r2(k+1)的估计准确率分别提升24.85%、29.01%、37.52%、31.63%,状态变量x1(k+1) 和x2(k+1)的估计准确率分别提升16.49%和18.43%。

三者之间存在着相互影响的关系,若加性干扰的滤波准确率提高,则加性干扰对模型的影响就会减弱,从而提高原始状态变量的估计精度,证明了本文所提方法的有效性。

4 结语

本文针对具有加性干扰的不确定系统设计了一种三阶段卡尔曼滤波器。本文提出建立加性干扰d(k)当前值的动态辅助方程和建立测量模型中r(k+1)的辅助方程,结合原始测量模型进行滤波;视加性干扰d(k)和r(k+1)的估计值为测量,设计原始状态变量x(k+1)的卡尔曼滤波器。仿真结果表明,该方法可以有效应对模型中的加性干扰,减少加性干扰对原始状态变量的干扰,能够有效实现滤波估计。