对数正态分布序列单均值变点的识别和估计

陈丽曲，黄介武

对数正态分布序列单均值变点的识别和估计

陈丽曲，黄介武

（贵州民族大学 数据科学与信息工程学院，贵州 贵阳 550025）

针对数据呈现偏态分布且存在变点的情况，构建对数正态分布的单均值变点模型，给出分布的均值单变点模型的似然函数，并采用极大似然方法和贝叶斯方法对变点位置进行识别和估计．通过模拟比较研究，这两种方法都能有效地估计变点位置，在标准差和相对误差准则下，贝叶斯方法比极大似然方法效果更理想．其中共轭先验分布下的贝叶斯方法较无信息先验下的贝叶斯方法识别和估计变点位置表现更优．

单均值变点；对数正态分布；贝叶斯方法；极大似然方法

变点是指一随机序列数据在某一个位置或时间点发生了分布或数字特征突然变化的点[1]，如果不考虑对变点进行识别和估计就进行统计分析则很可能导致结果具有误导性．变点问题多集中于基于正态分布的变点模型，包括正态均值、方差变点模型，正态单变点、多变点模型，正态线性回归模型中回归系数以及误差方差的变点模型．文献[2-4]运用似然比方法和贝叶斯方法详细讨论了一元正态以及多元正态均值或方差变点模型、正态回归变点模型中回归系数变点位置的识别和估计．文献[5]介绍了正态以及其他常见变点模型识别和估计的理论和方法，以及变点模型在各领域中的应用．文献[6]针对具有异质方差的正态模型的多变点估计问题，提出了一种基于贝叶斯模型选择过程的变点估计方法．赵江南[7]等运用ASAMC方法讨论了变点个数未知情况下正态分布变点的个数及位置识别．

针对数据呈现偏态且存在变点的情况，本文建立对数正态分布的单均值变点模型，探讨极大似然方法和贝叶斯方法在标准差和相对误差准则下识别和估计变点位置的优良性．

1　对数正态的单均值变点模型

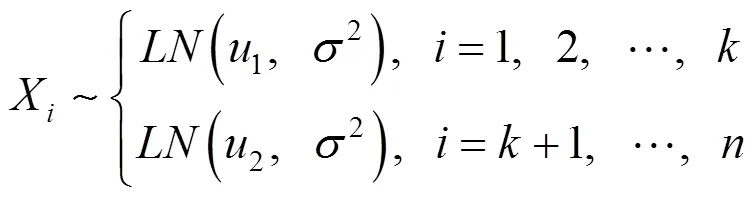
模型（2）的似然函数为

2　对数正态单均值变点的极大似然方法

3　对数正态单均值变点的贝叶斯方法

当使用贝叶斯方法分析问题时，为了获得更准确和可靠的统计推断结果，往往需要引入恰当的先验分布．然而，在实际应用中，有时缺乏关于先验分布的知识或信息，并且即使拥有这些知识，也可能不足以提供全面的先验分布．因此，引入无信息先验分布、共轭先验分布往往是一种合理可靠的选择．

3.1　无信息先验分布

取无信息先验分布

于是各参数的联合后验分布为

从而

类似地，有

3.2　共轭先验分布

从而

类似地，有

4　模拟研究

4.1　对数正态单均值变点的极大似然方法数值模拟

运用R软件进行对数正态分布极大似然方法的随机模拟，结果见表1．

表1　对数正态分布各参数的极大似然估计

图1　极大似然估计分布

图2　极大似然方法下变点k的轨迹

4.2　对数正态单均值变点的贝叶斯方法数值模拟

表2　两种先验分布下对数正态分布各参数的贝叶斯估计

表3　两种先验分布下不同变点位置的贝叶斯估计

图3 无信息先验下的Gibbs抽样迭代过程及多层迭代链轨迹

图4 共轭先验下的Gibbs抽样迭代过程及多层迭代链轨迹

4.3　随机模拟结果分析

4.3.1极大似然方法数和贝叶斯方法的比较由表1～2可以看出，本文采用的极大似然方法数和贝叶斯方

5　结语

本文通过构建对数正态单均值变点模型，采用极大似然方法和贝叶斯方法探讨了数据呈现偏态分布且存在变点的问题．通过研究比较可知，相较于极大似然方法，贝叶斯方法估计变点位置更精准．特别是在共轭先验分布下对数正态单均值变点的贝叶斯方法估计变点位置效果是最优的．

[1] PAGE E S．Continuous inspection schemes[J]．Biometrika，1954，41（1/2）：100-115．

[2] CHEN J．Inference About the Change Points in a Sequence of Gaussain Random Vectors Using Information Criterion[D]．Bowling Green：Bowling Green State University，1995．

[3] CHEN J，Gupta A K．Testing and locating variance changepoints with application to stock prices[J]．Journal of The American Statistical Association，1997，92（438）：739-747．

[4] CHEN J，Gupta A K．On change point detection and estimation[J]．Communications in Statistics Simulation and Computation， 2001，30（3）：665-697．

[5] Gurevich G，Vexler A．Retrospective change point detection：from parametric to distribution free policies[J]．Communications in Statistics Simulation and Computation，2010，39（5）：899-920．

[6] KANG S G，Lee W D，Kim Y．Bayesian Multiple Change-Points Detection in a Normal Model with Heterogeneous Variances[J]．Computational Statistics，2021，36（12）：1365-1390．

[7] 赵江南，周菊玲．正态分布序列变点识别问题探讨[J]．统计与决策，2019，35（15）：13-17．

[8] Fisher R A．Statistical Methods in Scientific Inference[M]．London：Oliver and Boyd，1956．

[9] Bickel P J，Doksum K A．Mathematical Statistics：Basic and Selected Topics（Vol 1）[M]．San Francisco：Holden-Day，1977．

[10] ZHANG Fengqing，GOU Jiangtao．A unified framework for estimation in lognormal models[J]．Journal of Business & Economic Statistics，2022，40（4）：1583-1595．

[11] Lyu J，Nadarajah S．Discrete lognormal distributions with application to insurance data[J]．International Journal of System Assurance Engineering and Management，2021（1）：1-15．

[12] 陶鹤，刘伟，付晶园．对数正态分布可靠性模型及应用[J]．统计与决策，2019，35（3）：89-92．

[13] Jandhyala V K, Fotopoulos S B. Estimating the unknown change point in the parameters of the lognormal distribution[J]. Environmetrics，2007，18（2）：141-155.

Identification and estimation of single mean change points in lognormal distribution sequences

CHEN Liqu，HUANG Jiewu

（School of Data Science and Information Engineering，Guizhou Minzu University，Guiyang 550025，China）

In response to the situation where the data presents a skewed distribution and there are change points，a single mean change point model with a lognormal distribution is constructed．The likelihood function of the mean single change point model for this distribution is given，and the maximum likelihood method and Bayesian method are used to identify and estimate the position of the change points．Through simulation and comparative research，both methods can effectively estimate the position of the change point．Under the criteria of standard deviation and relative error，the Bayesian method is more effective than the maximum likelihood method．The Bayesian method under conjugate prior distribution performs better in identifying and estimating the position of change points compared to the Bayesian method without prior information.

single mean change point；lognormal distribution；Bayesian method；maximum likelihood method

1007-9831（2023）12-0015-07

O212.1

A

10.3969/j.issn.1007-9831.2023.12.003

2023-05-28

贵州省科技计划基金项目（黔科合基础[2017]1083号）；贵州省教育厅自然科学研究项目（黔教技[2022]015号）

陈丽曲（1997-），女，贵州道真人，在读硕士研究生，从事统计模型与统计计算研究．E-mail：2290167300@qq.cm

黄介武（1977-），男，湖南益阳人，教授，博士，从事统计模型与统计计算研究．E-mail：846221886@qq.com