带有反应项的可压缩微极实际气体模型解的指数稳定性
2024-01-17王玉黄兰
王玉,黄兰
带有反应项的可压缩微极实际气体模型解的指数稳定性
王玉,黄兰
(华北水利水电大学 数学与统计学院,河南 郑州 450046)
研究了齐次边界条件下一维粘性带有反应项的可压缩微极实际气体模型解的大时间行为.假定任意初始值(密度不含真空),利用能量估计和各种精细的插值不等式证明密度函数和温度函数的一致上下界,进而证明了解的整体存在性和指数稳定性.
带有反应项流体;微极实际气体;存在性;先验估计;指数稳定性
1 引言及预备知识
流体力学主要研究流体(液体和气体)的力学运动规律及其应用,经典的流体力学模型包括Navier-Stokes方程、磁流体方程、微极流体模型以及磁微极流体模型等.1964年,文献[1]首次描述了微极流体模型,该模型可用于对具有微观结构的材料的研究,一开始就受到许多研究者的关注.微极流体的数学理论研究分为两个方向:可压缩微极流体和不可压缩微极流体.不可压缩微极流体是一种相对理想的状态,目前已有大量研究.关于可压缩微极流体,在三维情况下,文献[2-6]研究了具有球对称的粘性可压缩微极流体模型解的整体存在性和具有圆柱对称的粘性可压缩微极流体解的整体存在性以及指数稳定性.而在一维情况下,关于可压缩微极流体模型解的存在性与正则性也有大量研究[7-13],其中文献[11-12]研究了理想气体模型经典解的存在性,文献[13]研究了可压缩微极实际气体模型解的整体存在性.在微极实际气体模型的基础上增加反应项后,文献[14]研究了齐次边界条件下带有反应项的粘性可压缩微极实际气体模型的局部解存在性.但对于该一维模型整体解的存在性以及大时间性态,还没有相关研究.本文在文献[14]基础上进一步研究齐次边界条件下粘性反应微极实际气体一维模型解的大时间行为.
在拉格朗日坐标系下,带有反应项的粘性可压缩微极实际气体模型方程为
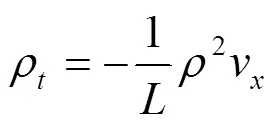



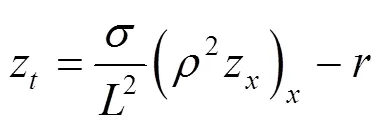
假设系统(1)~(5)满足初值条件
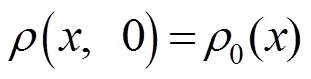
和边界条件
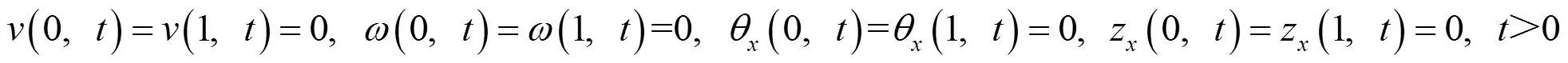
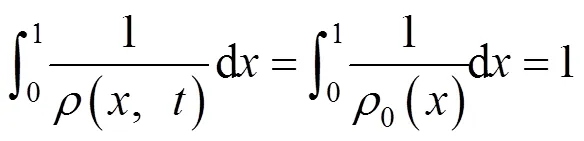
2 解的整体存在性
定理1假设初值满足
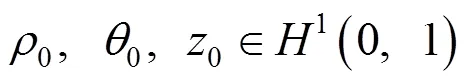


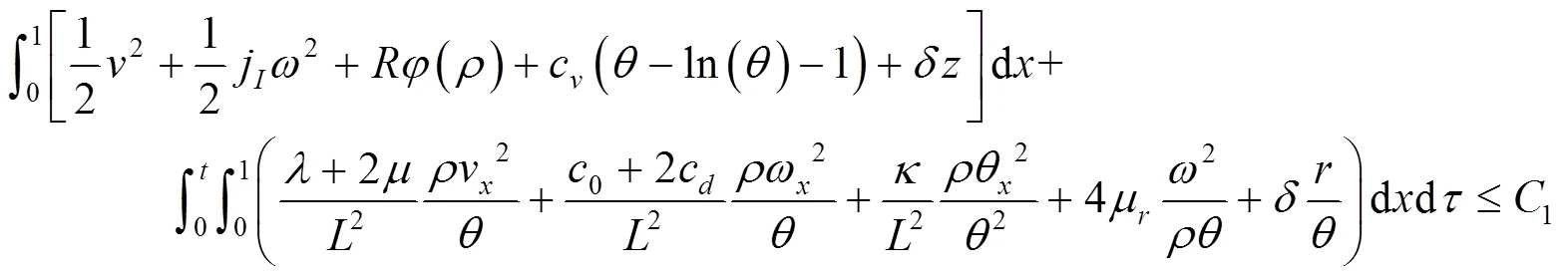
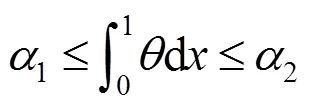
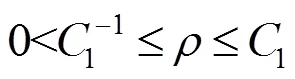

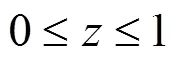
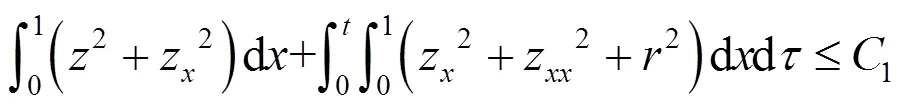
令

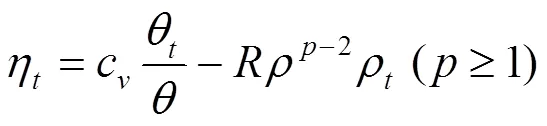
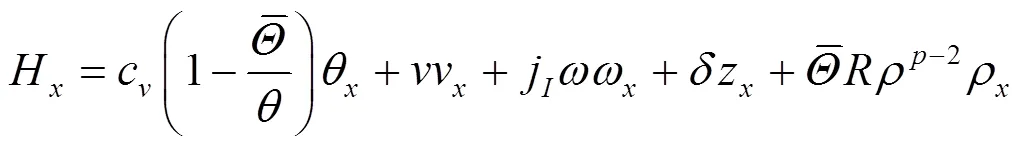
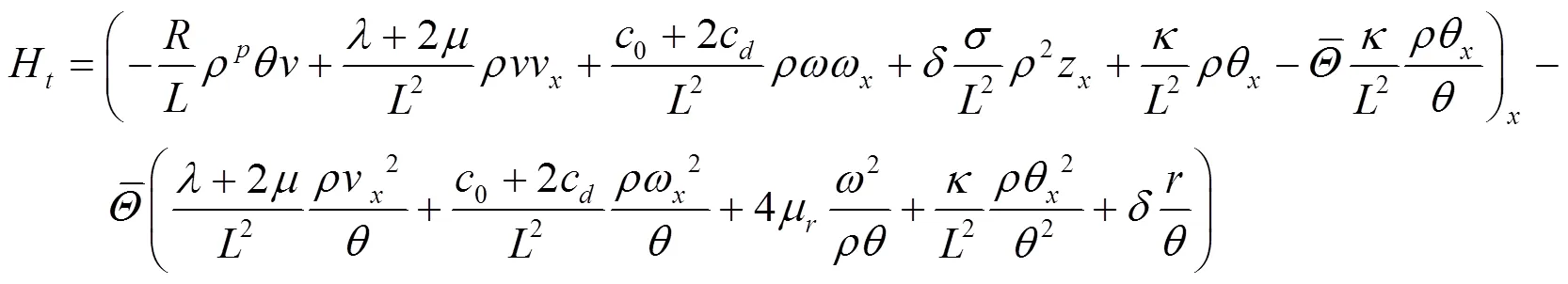
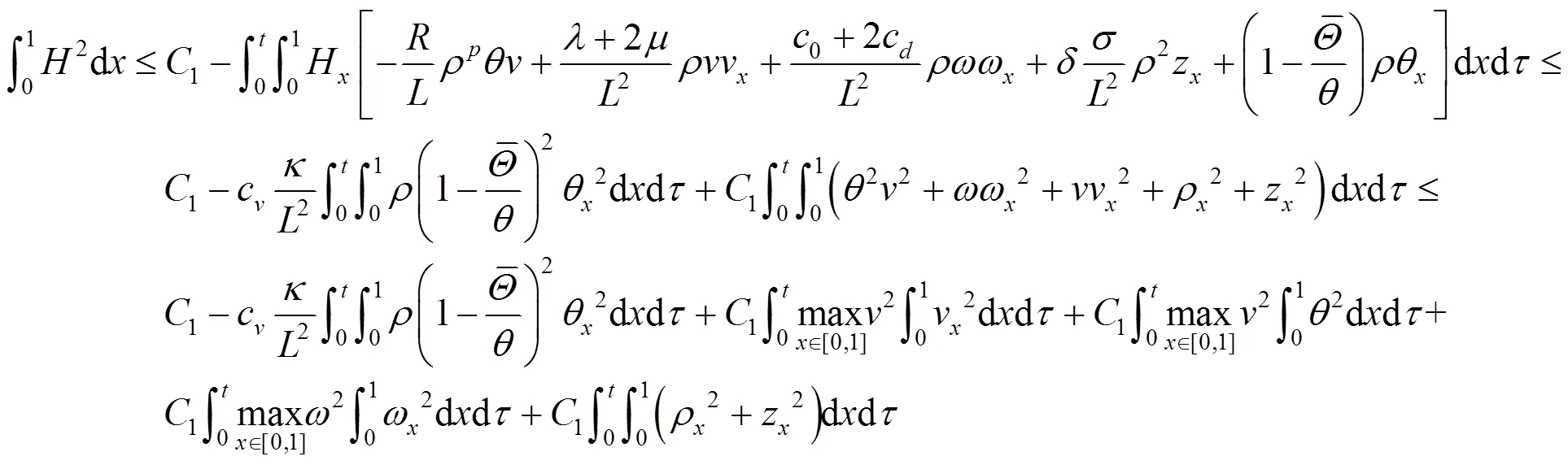

结合边界条件(7),并利用插值不等式,由式(12)可得
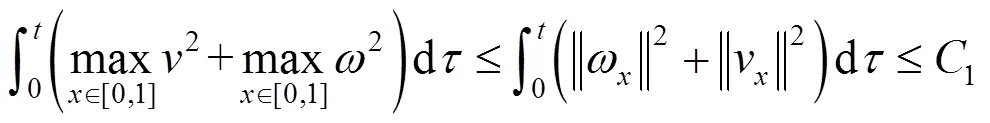
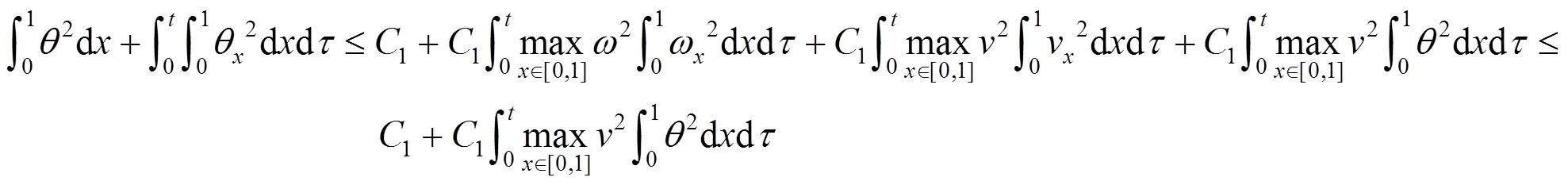
利用引理2并结合式(22),由式(23)可得
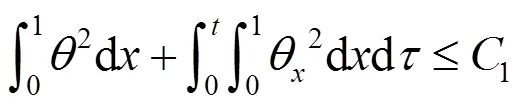
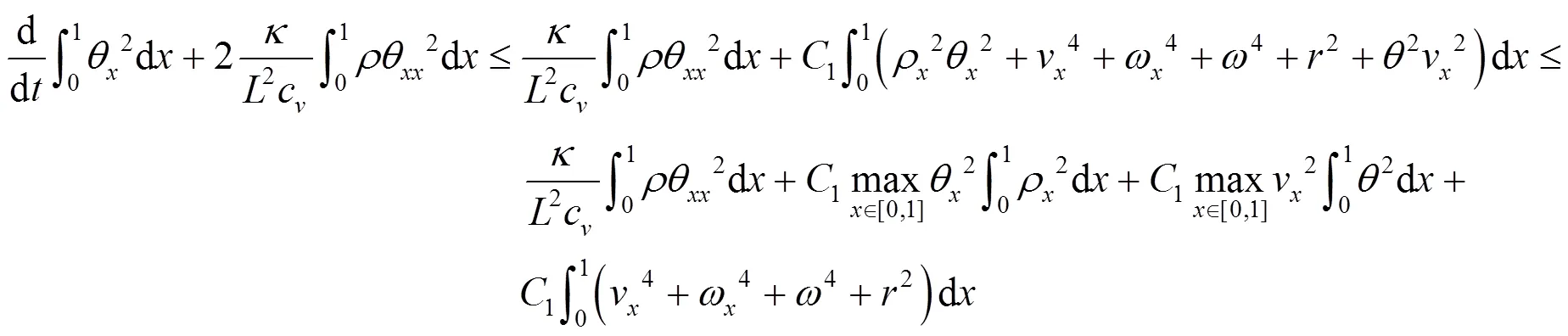

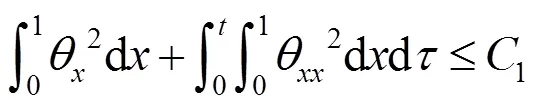
由式(27)和引理1中Young不等式可知


由式(24)(29)可知
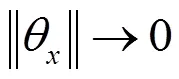
由式(28)(30)可知
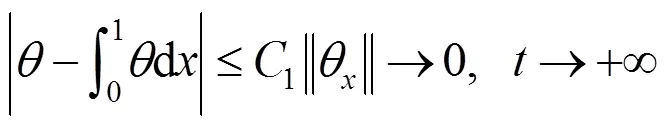
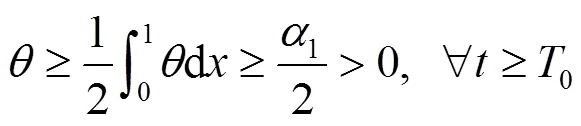
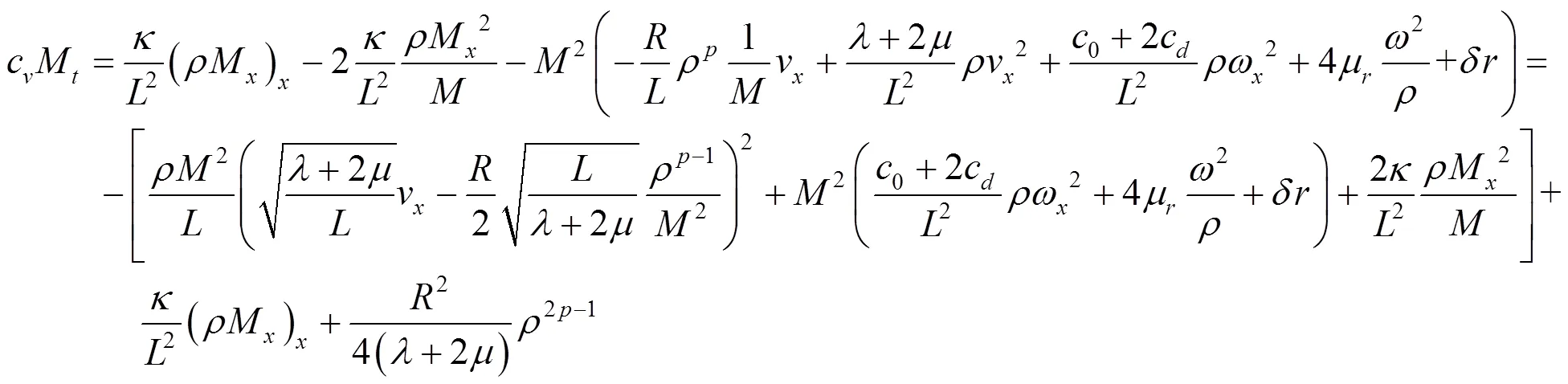
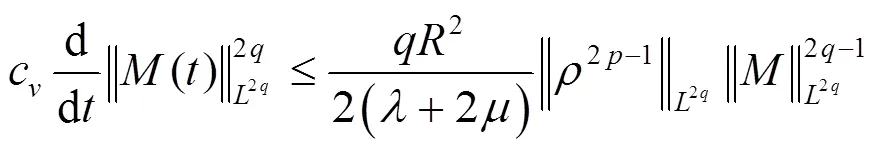
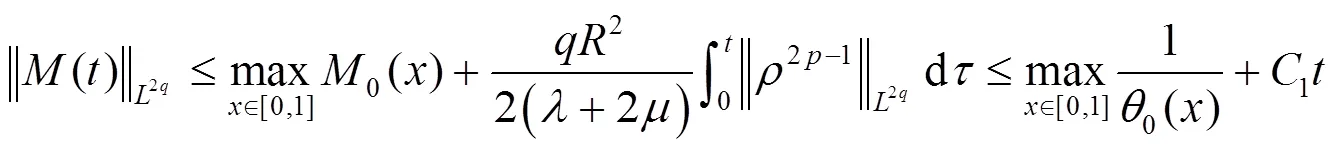


由式(28)(37),易得
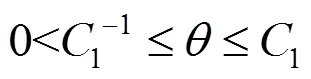
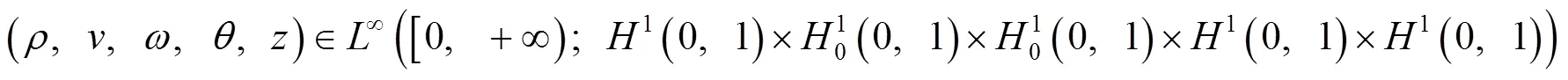
3 解的指数稳定性

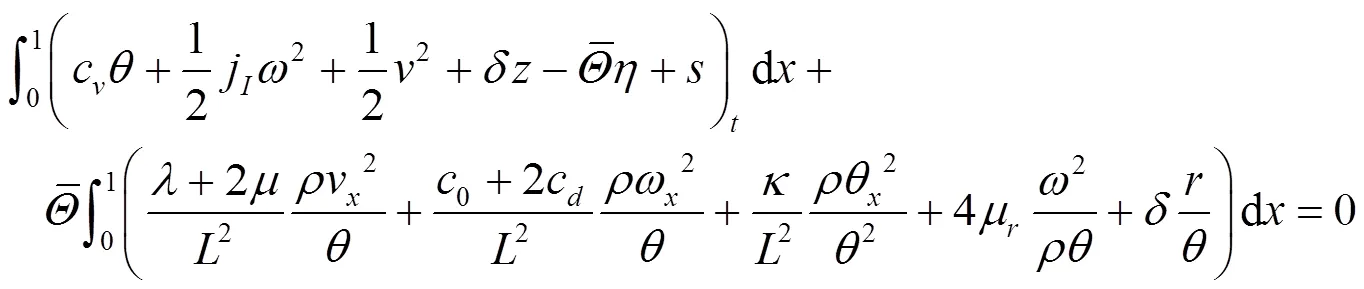
结合式(11)(38),有
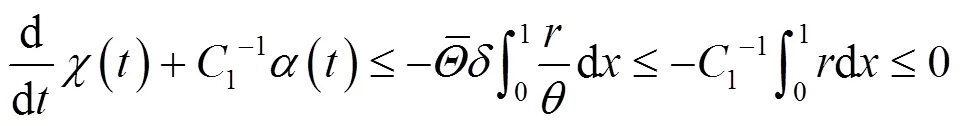
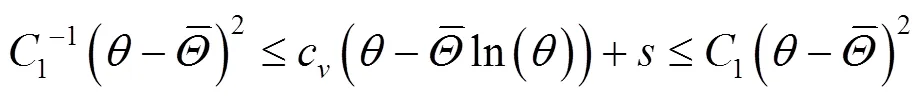

将式(42)(43)相加,得
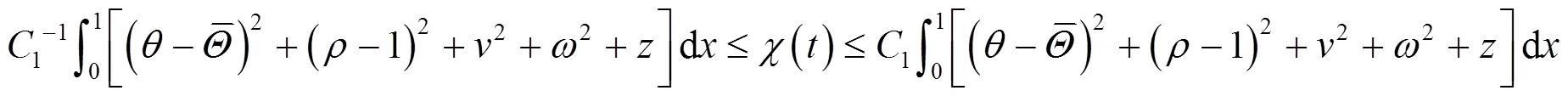
再结合式(8)(38),利用引理3中Poincaré不等式,有
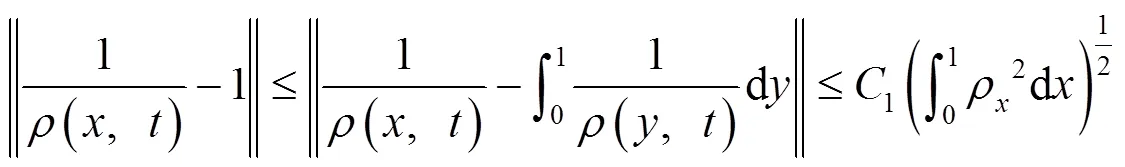
结合式(11)(38)(44)(45),利用引理3中Poincaré不等式,有
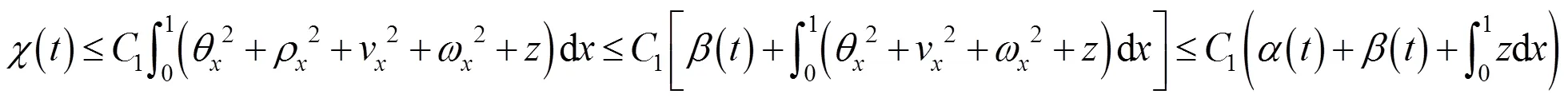
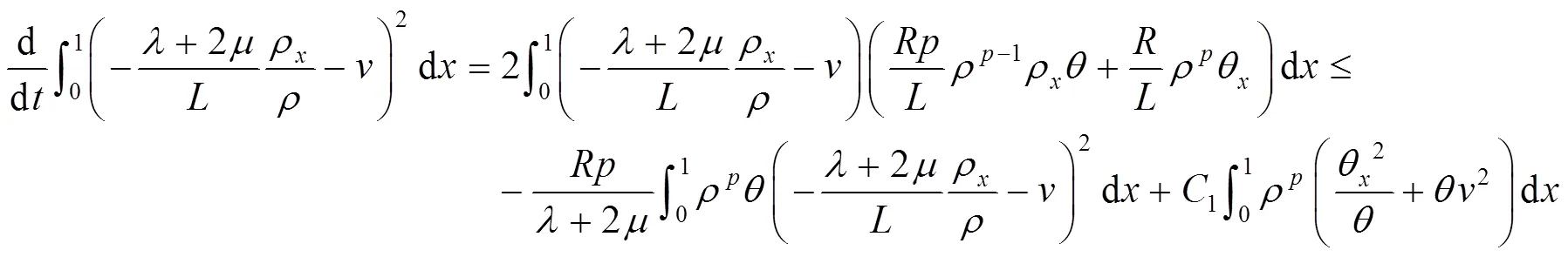
由式(11)(38)(47),再利用引理3中Poincaré不等式,得到
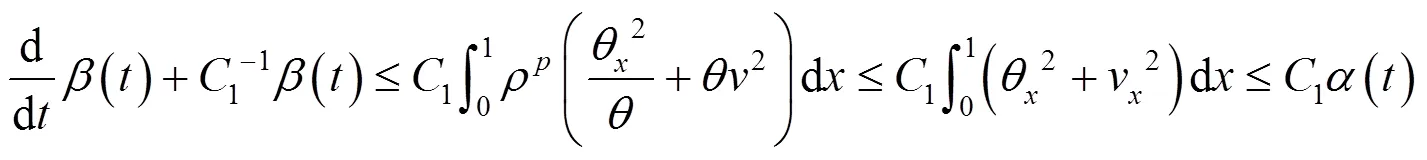
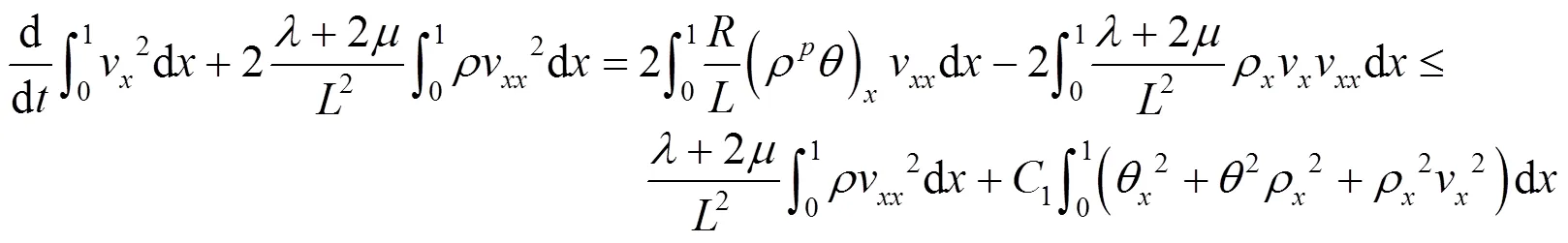
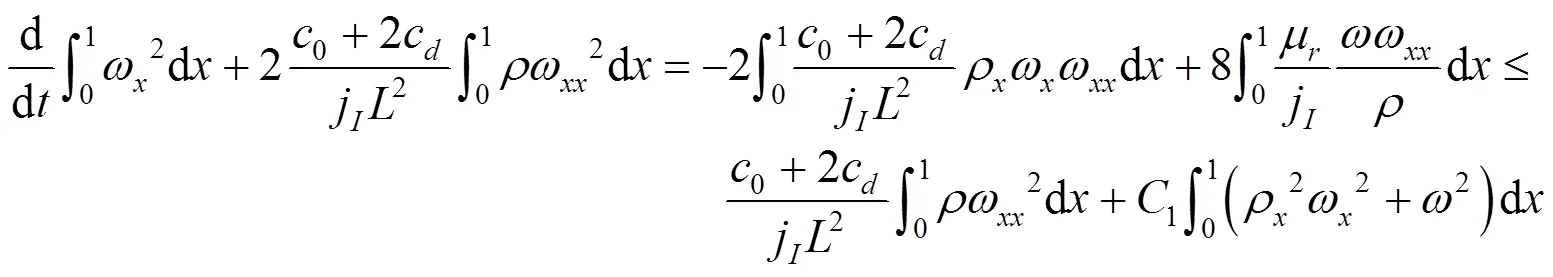
结合式(25)(38)(49)(50),利用引理3中Poincaré不等式,得到
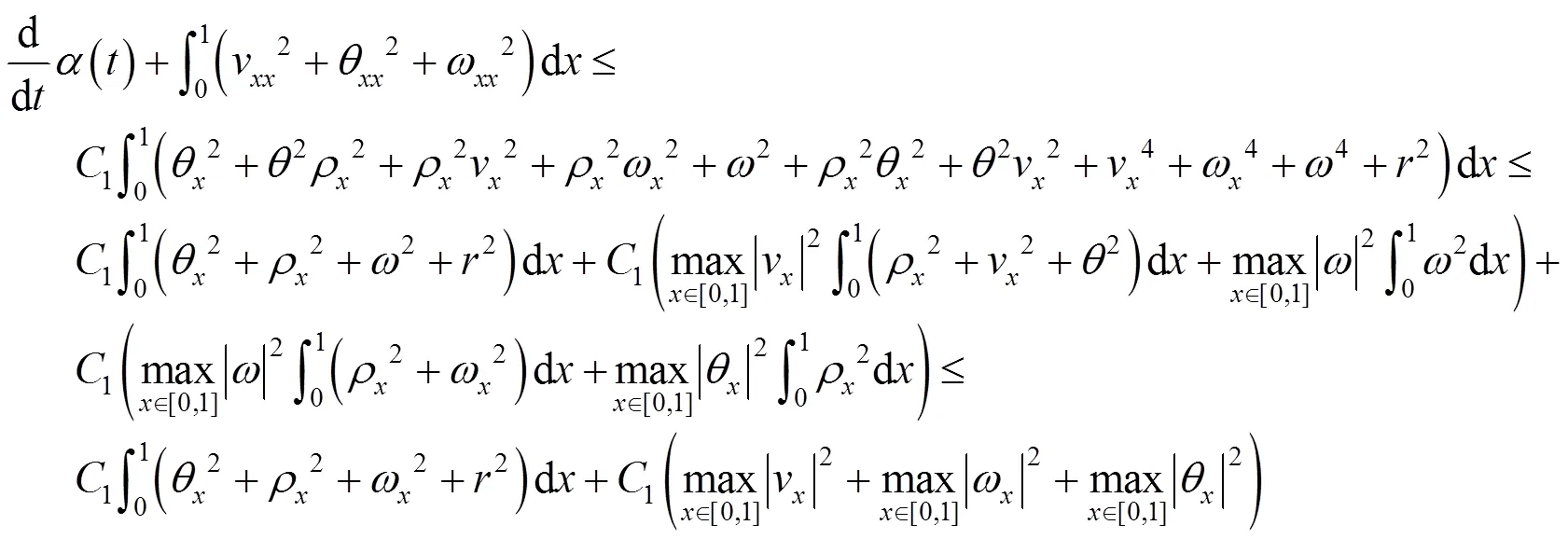
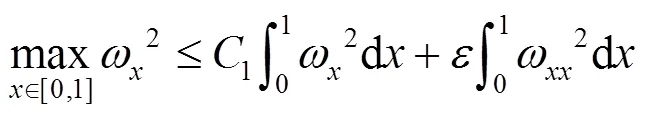
再结合式(26)(51)(52),有

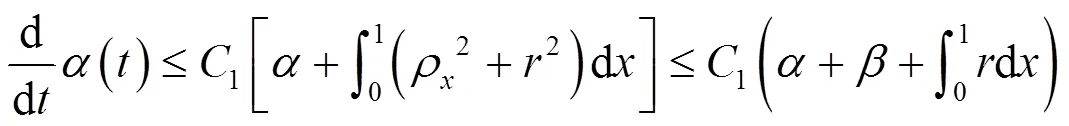

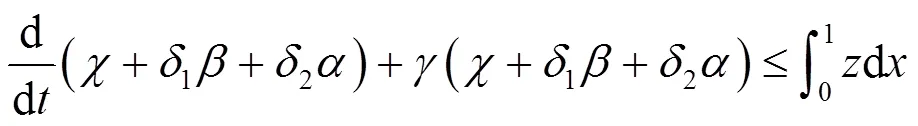
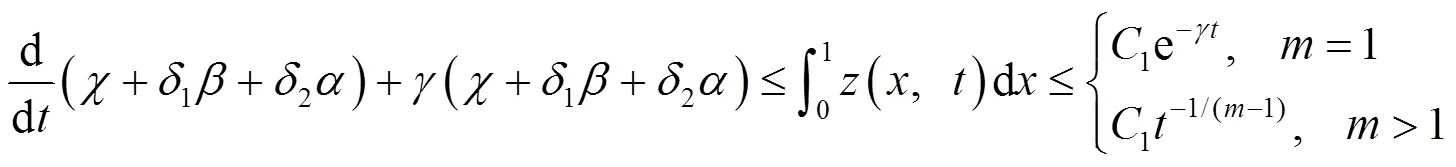
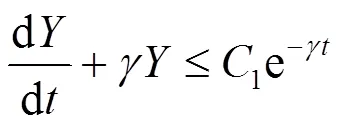

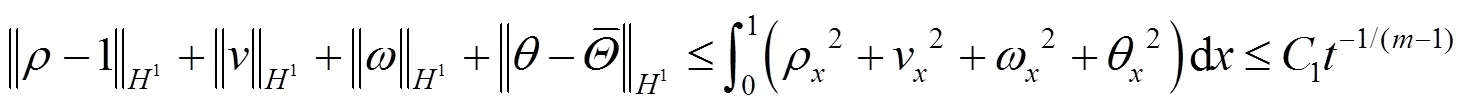
结合式(14)(57)(58)(60),得到
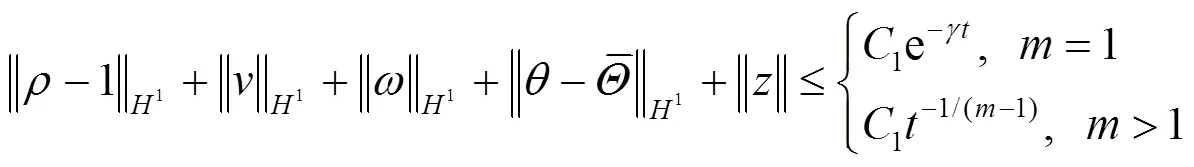
证毕.
由式(62)可得定理2解的指数稳定性.
4 结语
通过严密的推理,本文证明了在齐次边界条件下带有反应项的可压缩微极实际气体模型整体解的存在性与指数收敛性.但在粘性系数依赖于温度和密度的情况下,带有反应项的可压缩微极实际气体模型解的整体存在性和大时间性等一系列性质还有待证明.
[1] ERINGEN C A.Simple microfluids[J].Int J Eng Sci,1964,2(2):205-217.
[2] DRAZIC I.Three-dimensional flow of a compressible viscous micropolar fluid with cylindrical symmetry:a global existence theorem[J].Math Method Appl Sci,2017,40(13):4785-4801.
[3] DRAZIC I,MUJAKOVIC N.3-D flow of a compressible viscous micropolar fluid with spherical symmetry:a local existence theorem[J].Bound Value Probl,2012(69):113-118.
[4] DRAZIC I,MUJAKOVIC N.3-D flow of a compressible viscous micropolar fluid with spherical symmetry:a global existence theorem[J].Bound Value Probl,2015(98):1-21.
[5] DRAZIC I,MUJAKOVIC N.Local existence of the generalized solution for three-dimensional compressible viscous flow of micropolar fluid with cylindrical symmetry[J].Bound Value Probl,2019(16):16-42.
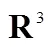
[7] DRAZIC I,SIMCIC L.One-dimensional flow of a compressible viscous and heat-conducting micropolar fluid with homogeneous boundary conditions:A brief survey of the theory and recent progress[J].Global and Stochastic Analysis,2018,5(1):45-55.
[8] MUJAKOVIC N.One-dimensional flow of a compressible viscous micropolar fluid:A local existence theorem[J].Glas Mat,1998,33(1):71–91.
[9] MUJAKOVIC N.Nonhomogeneous boundary value problem for one-dimensional compressible viscous micropolar fluid model:regularity of the solution[J].Bound Value Probl,2008(1):189748-189762.
[10] MUJAKOVIC N.The existence of a global solution for one dimensional compressible viscous micropolar fluid with non-homogeneous boundary conditions for temperature[J].Nonlinear Anal:Real World Appl,2014(19):19–30.
[11] LI F,ZHU H.Global classical large solution to compressible viscous micropolar and heat-conducting fluids with vacuum[J].Discrete Cont Dyn-A,2019,39(6):3069-3097.
[12] ZHEN Lei,LIN Fenghua.Global mild solutions of Navier-Stokes equations[J].Commun Pur Appl Math,2011(9):1297-1304.
[13] BASIC-SISKO A,DRAZIC I.Global solution to a one-dimensional model of viscous and heat-conducting micropolar real gas flow[J]. J Math Anal Appl,2021,495(1):124690-124715.
[14] BASIC-SISKO A,DRAZIC I.Local existence for viscous reactive micropolar real gas flow and thermal explosion with homogeneous boundary conditions[J].J Math Anal Appl,2022,509(2):125988-126018.
[15] ZHENG S . Nonlinear Evolution Equations[J].American Mathematical Society,2005(42):1-42.
[16] SONG Jiang.Large-time behavior of solutions to the equations of a viscous polytropic ideal gas[J].Ann Math Pura Appl,1998(175):253-275.


Exponential stability of solutions to the compressible viscous and reactive micropolar real gas model
WANG Yu,HUANG Lan
( School of Mathematics and Statistics,North China University of Water Resources and Electric Power,Zhengzhou 450046,China)
The large-time behavior of solutions to the one-dimensional compressible viscous and reactive micropolar real gas model with homogeneous boundary conditions is studied.Based on the assumption that any initial value (mass density without vacuum),theuniform upper and lower bounds of the density and the temperature function are proved by using energy estimate method and delicate interpolation inequality,and then the global existence and exponential stability of solutions are obtained.
reactive fluid;micropolar real gas;existence;aprior estimate;exponential stability
1007-9831(2023)12-0001-08
O175
A
10.3969/j.issn.1007-9831.2023.12.001
2023-05-02
国家自然科学基金项目(11501199)
王玉(1999-),女,河南开封人,在读硕士研究生,从事偏微分方程研究.E-mail:wangyu1115598@163.com
黄兰(1982-),女,河南信阳人,教授,博士,从事偏微分方程研究.E-mail:huanglan82@hotmail.com
