基于BN 与NSGA-II 的装配式建筑施工风险控制研究
2024-01-17张永辉ZHANGYonghui
张永辉 ZHANG Yong-hui
(安徽工业大学管理科学与工程学院,马鞍山 243002)
0 引言
装配式建筑因其具有施工方便、节约资源、缩短工期等显著优势,已成为国内外建筑业发展的热点。当前,我国的装配式建筑处于初级阶段,在预制构件的生产、运输、存放、吊装等环节还存在缺陷,导致面临施工安全情况差、风险控制能力弱的问题。如何有效地对装配式建筑施工风险进行控制成为学界亟需解决的问题。
在施工风险评估方面,丁彦等[1]通过运用层次分析法及ABC 分类法,对风险因素进行分类排序评估,并提出了应对措施。李政道等[2]运用模糊层次综合评价法对装配式建筑从设计到完工过程中的风险因素进行评价管理,制定了相应的措施方案。
在施工风险控制措施选择方面,Klein 等[3]通过权衡项目工期、成本和质量目标,获取风险控制措施策略。杨莉等[4]以风险应对成本和期望风险损失最小化为目标,构建了风险控制措施优化模型。现有文献虽然取得了一定的成果,然而,也存在一定的不足。例如基于权衡思想的措施选择方法缺少数学方案;基于优化思想的措施选择方法较为完善,但没有考虑风险之间相关性。
基于此,本文借助模糊贝叶斯网络量化风险间的因果关系,利用反向诊断确定关键的风险因素,在此基础上构建了考虑风险相关性的多目标优化模型,并基于NSGA-II算法对模型进行求解。本文的研究能够为施工风险管理提供合理的控制策略。
1 装配式建筑施工风险因素确定
通过分析2018-2021 年各地施工事故的发生原因,紧密结合《施工企业安全生产评价标准》(JGJ/T 77-2010)、《建筑施工安全检查标准》(JGJ 59-2011)等标准规范,归纳整理出频率较高的致因因素,从人、材料设备、技术与环境4 个方面构建了装配式建筑施工风险评估体系。如图1所示。
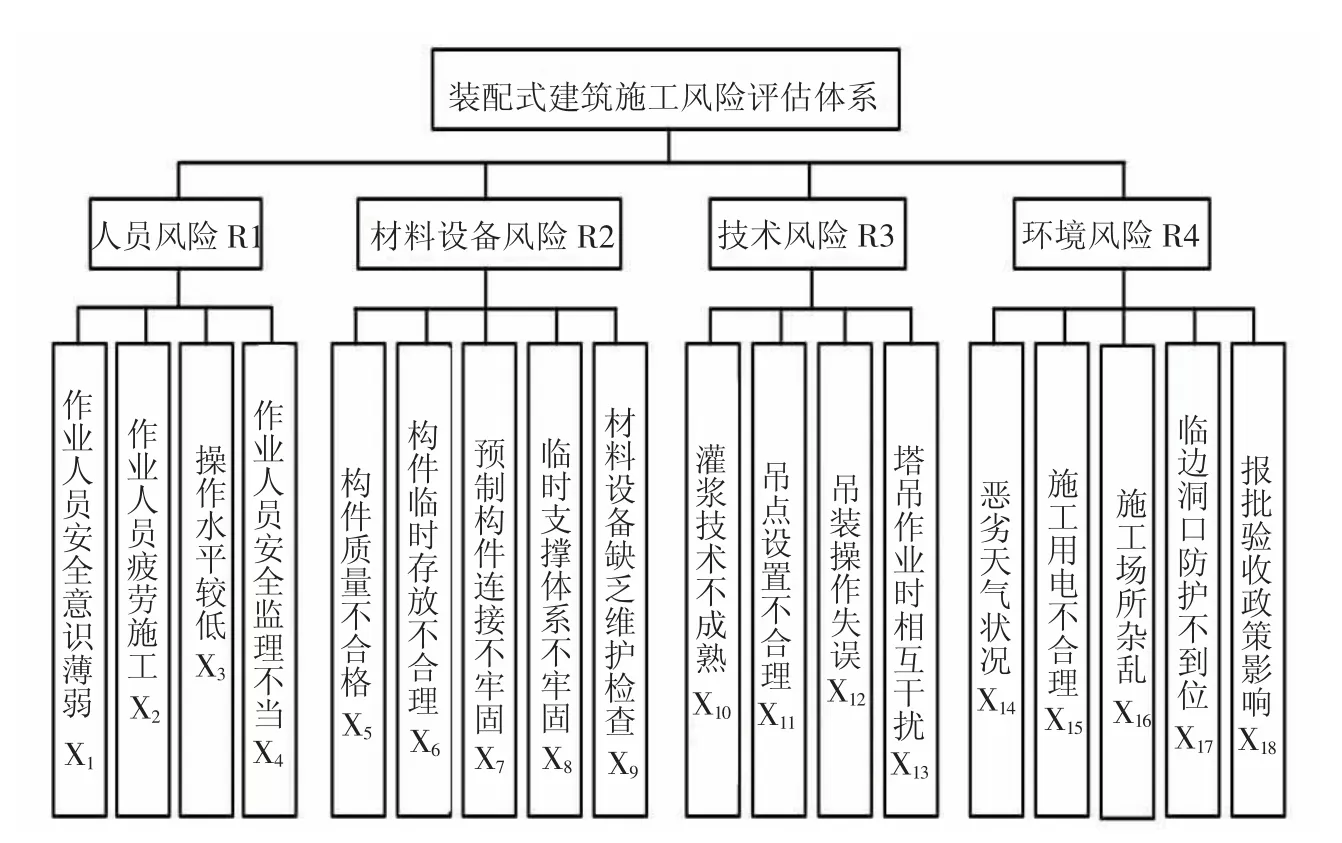
图1 装配式建筑施工风险评估体系
2 装配式建筑施工风险评估
2.1 构建贝叶斯网络结构
贝叶斯网络结构通常由专家知识或机器学习获得,专家知识建模存在一定主观性,机器学习建模受数据、方法等因素影响,随机性太强,单一方法都存在一定缺陷。鉴于此,本文首先基于K2 算法对装配式建筑施工风险进行结构学习;最后,根据专家的经验优化贝叶斯网络结构[5]。
2.2 获取贝叶斯网络参数
由于现阶段装配式建筑施工风险数据较少且获取难度大,因此节点参数主要依靠专家的经验与知识判断获得,但存在一定的主观性。鉴于此,本文将三角模糊数引入贝叶斯网络中来表示事件发生的概率。假设每个节点由两个状态组成(Y 和N),(Y,N 分别代表发生与不发生)。三角模糊数由(a1,a2,a3)表示,具体如表1 所示。
由于专家的工作经验和知识储备存在差异,所以需要将不同专家的意见进行聚合。本文采用相似度聚合法(similarity aggregation method,SAM)处理专家的意见。
2.3 贝叶斯网络反向推理
将先验概率与条件概率输入到贝叶斯网络结构中,借助贝叶斯网络反向诊断可以得到各子节点的后验概率,对节点的重要性进行排序,从而识别关键风险因素。
3 装配式建筑施工风险控制措施优化
3.1 构建风险控制措施多目标优化模型
在施工过程中,各种风险往往是相互关联的,从风险定义来看,涉及风险发生概率和风险损失两个方面,因此风险相关性主要从风险概率和风险损失两方面来考虑。其中以条件概率量化风险概率的相关性,具体公式如式(1)所示;风险损失的相关性借助2-可加模糊测度来度量。
假设m 为与风险Ri相关的风险数量,表示在风险Rj不发生时风险Ri的发生概率,表示在风险Rj发生时风险Ri的发生概率,考虑风险相关性后风险Ri的概率为:
已有学者提出一种利用属性权重和相关系数确定2可加模糊测度的方法[6],具体如下:
式中,mi和mij分别是属性xi和属性{xi,xj}的默比乌斯变换系数,P 为所有单个属性与两两属性的重要程度之和,γij为属性xi与xj的相关系数,wi为属性xi的权重。
式中,Li为第i 个风险的初始损失值,Li,k为第i 个风险采取第k 项风险控制措施的损失值,TLi为采取全部风险控制措施下风险i 的损失值,TLik为未采取风险控制措施k 的下风险i 的损失值,ui,k为第i 个风险实施第k 项措施的模糊测度。
在构建模型之前,需要对涉及到的参数进行说明:R={R1,R2,…Rn}为关键风险因素的集合;S={S1,S2,…Sm}为风险控制措施的集合;eik为风险控制措施对风险的作用效果;PIik为采取控制措施k 后风险因素Ri的发生概率,V为风险的期望效益值;ti为风险因素i 发生时造成延期的天数,tik为对风险因素i 采取控制措施k 后提前的天数;Tmax为风险因素造成工期延迟的最大期限值;RC 为风险控制措施总成本,Ck为采取风险控制措施Sk的成本,Cmax为风险控制措施的预算;M 表示存在先后顺序的风险控制措施集合表示相互排斥的风险控制措施集合。
其中,式(5)为目标函数,表示最大化期望效益与最小化措施成本;式(6)表示项目必须在规定的时间内完成;式(7)表示风险控制措施的成本要在预算之内;式(8)表示风险控制措施对风险的作用效果,当eik=1 时,表明风险控制措施对该风险有效,反之,eik=0;式(9)表示当风险控制措施存在相互排斥的关系时,至多只能选择一个风险控制措施;式(10)表示当风险控制措施存在先后顺序时,只能按先后顺序实施;式(11)表示是否采取风险控制措施,当Sk=1 时,表明采取该措施,反之,Sk=0。
3.2 基于非支配排序遗传算法的模型求解
根据风险控制措施多目标优化模型的特点,设计基于NSGA-II 算法求解该模型[7]。该算法基本的思想是首先采用快速非支配排序对种群中的个体进行非支配排序确定所在层级,降低算法的复杂度;然后通过计算拥挤度选择同级中较优的个体,增加了种群的多样性;最后引入精英保留的策略保证优秀个体能够容易保存。
3.3 基于TOPSIS 的Pareto 集方案排序
根据NSGA-II 算法所求得Pareto 最优解集,由Pareto最优解集中的元素构成m 个备选方案,其属性n 为每个最优解的目标函数值,利用TOPSIS 法对不同的最优解进行分析、评价,从中选出最佳的折中解。具体步骤如下[8]:
①指标正向化。对各评价指标进行正向化处理,转化为极大型指标。
②构造规范化矩阵。利用向量归一化的方法进行处理,得到规范化矩阵Z。
③确定正负理想解s+和s-。分别为矩阵的每列元素的最大值与最小值。
④计算各方案与正负理想解的加权距离d+和d-,进而得到相对贴近度d。
式中,ωj为第j 个属性权重,即目标函数的权重;di越接近于1,说明方案越优。
4 案例分析
4.1 工程概况
某一项目位于山东省济南市历下区,地上总建筑面积28973.58m2,计划建设6 栋11 层的住宅楼,结构类型为整体式剪力墙。单体装配率达到66%。PC 构件类型包括预制外墙板、预制PCF 板、预制楼梯、预制叠合板、预制飘窗。
4.2 风险评估
4.2.1 构建贝叶斯网络结构
本文通过专家知识和机器学习相结合的方法建立贝叶斯网络结构,如图2 所示。
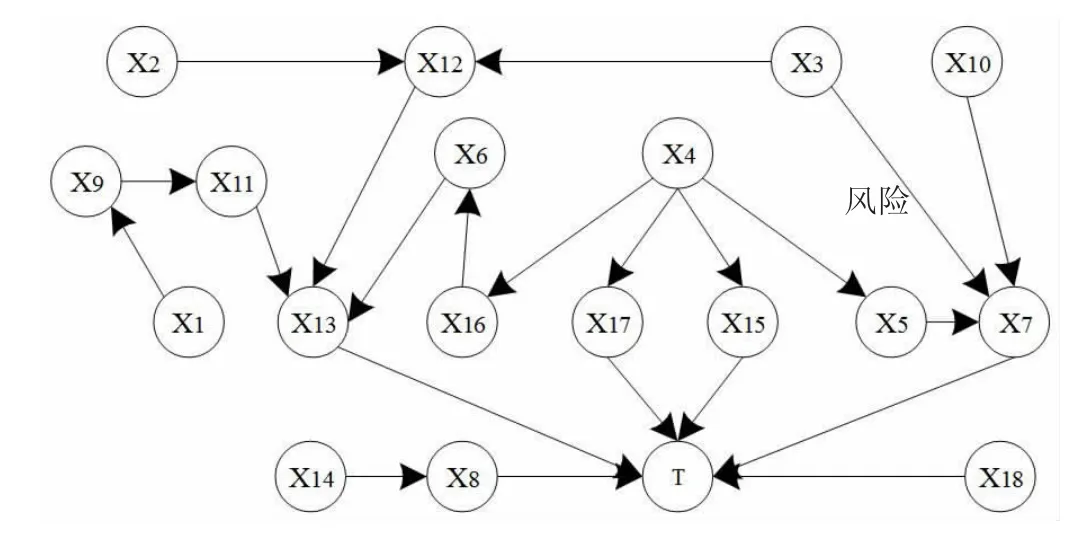
图2 装配式建筑施工风险贝叶斯网络
4.2.2 获取贝叶斯网络参数
邀请5 位相关领域的专家,采取匿名的方式对根节点发生的概率给出意见。基于SAM 法处理专家意见得到根节点的先验概率。根节点的先验概率如表2 所示。

表2 根节点专家评判语义值及先验概率
4.2.3 贝叶斯网络推理结果
通过计算得到了根节点的先验概率与非根节点的条件概率,假设装配式建筑施工风险(T)的发生概率为100%,借助GeNIe3.0 软件,得到各节点的后验概率,结果如图3 所示。根据后验概率值,装配式建筑施工关键风险因素为作业人员操作水平X3、安全监理不当X4、预制构件质量不合格X5、预制构件连接不牢固X7、临时支撑体系不牢固X8、塔吊作业时相互干扰X13、临边、洞口安全防护X17、报批验收政策法规影响X18。

图3 贝叶斯网络反向推理结果
4.3 算法求解及结果分析
通过模糊贝叶斯理论识别了关键风险因素,在此基础上梳理了关键风险因素的控制措施及实施成本,借助一些具有相似风险的项目,通过这些项目的风险应对策略来确定备选风险控制措施,结果如表3 所示。其中无相互排斥的风险控制措施,即,S9、S10;S11、S12为存在先后顺序的风险控制措施,即。在考虑风险概率和损失相关性下部分风险发生的概率、损失、工程延期天数如表4 所示。

表3 部分关键风险因素的控制措施及成本
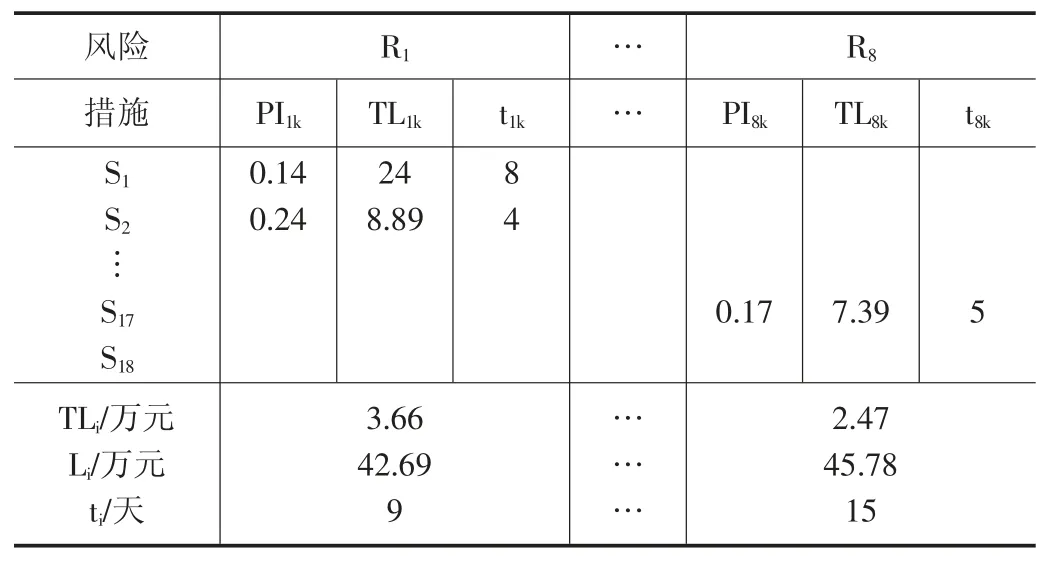
表4 风险-控制措施结构矩阵
基于以上相关数据信息,设定工期延迟的最大期限值Tmax=15 天,风险控制措施的预算为Cmax=100 万元,NSGAII 算法的种群规模为100,迭代次数为200,交叉概率为0.8,变异概率为0.1,考虑风险相关性前后的优化结果如图4 所示。

图4 未考虑与考虑风险相关性的优化结果
在考虑风险相关性的情况下,NSGA-II 算法生成18个分布较为分散的Pareto 最优解,随着措施成本增加,措施期望效益值也逐渐增加。
由表5 可知,当选取风险控制措施S1、S3、S4、S5、S8、S9、S10、S11、S12、S13,此时风险控制措施效益为21.53,风险控制措施成本为87.4 万元,选取的风险控制措施集合达到最优的风险应对效果。

表5 风险控制措施的优化结果
5 结论
该模型可准确识别施工关键风险因素,与不考虑风险相关性的情况相比,考虑风险相关性情况下的措施期望效益更小,这说明风险相关性会影响风险控制措施的选取。TOPSIS 法有效地平衡了措施期望效益与成本,决策者能够选取最优的风险控制措施集合,为实际工程中的风险应对提供支持。
