膨胀岩湿胀本构研究综述

赵二平 ZHAO Er-ping；张聪 ZHANG Cong；李建林 LI Jian-lin；蒋尚家 JIANG Shang-Jia；车德龙 CHE De-long

（三峡大学防灾减灾湖北省重点实验室，宜昌 443002）

0 引言

膨胀岩是指遇水后产生体积膨胀和软化现象的岩石，在我国分布广泛，按矿物组成成分不同，膨胀岩大体可以分为两类：一类是诸如泥岩、黏土岩等含有蒙脱石、伊利石、高岭石等强烈亲水性矿物的岩石，另一类是诸如硬石膏、无水芒硝等遇水后产生化学作用的岩石[1]。膨胀岩对工程建筑的危害，既表现在边坡、路面、地基上，也表现在地下硐室、隧道围岩、衬砌等工程建筑中。迄今为止，全球已有40 多个国家和地区报道过与膨胀岩相关的工程灾害。例如Wagenburg 北部隧洞，27 年连续观测，累积最大底鼓量1029mm，且仍无衰减趋势[2]；南昆铁路家竹箐隧道，底板上鼓变形最大1000mm[3]，诸如此类工程问题报导众多。事后调查分析认为，膨胀岩遇水产生体积膨胀是出现众多工程问题的关键因素之一。

目前，众多学者利用不同的试验和测试分析方法进行了膨胀岩吸水量、膨胀变形、膨胀力、膨胀应变、强度以及微观结构方面的研究，取得了丰富的研究成果。在膨胀岩湿胀本构研究方面，诸多学者也通过试验及理论分析，建立了不同的本构模型。本文梳理了膨胀岩湿胀本构关系建立方法的相关进展，并在此基础上提出未来应着重依据实际工程条件，建立综合考虑施工期开挖卸荷效应及运行期运行荷载的膨胀岩湿胀本构关系。

1 膨胀岩湿胀本构关系研究进展与分析

1.1 基于Huder-Amberg 模型

1970 年Huder-Amberg 采用常规固结仪对泥灰岩进行了单轴膨胀试验，发现轴向膨胀应变与轴向膨胀压力的对数之比呈线性关系，之后Grob[4]利用数学关系式对此进行表述，得到了最初的膨胀本构关系式，如式（1）所示：

式中：ε 为轴向应变；σ0为最大膨胀压力；σ 为膨胀压力；K 为σ=0.1MPa 时的轴向膨胀率。

Einstein[5]和Wittke[6]根据Huder-Amberg 单轴试验结果，假设膨胀应变是由于应力第一不变量的改变所引起的，并假设轴向应力与径向应力符合金尼克条件，由此将一维情况推导至三维，从而建立了三维膨胀本构。杨庆等[7]（1995 年）根据膨胀岩三轴膨胀试验结果，验证了Einstein和Wittke 关于三维膨胀本构的假说中第一条“膨胀应变是由于应力第一不变量的改变所引起的”是正确的，并指出第二条“Huder-Amberg 单轴试验的轴向应力与径向应力符合金尼克条件”是不完善的，因为侧向膨胀应力是试件吸水膨胀引起的，是一种主动的力，并非由轴向压力引起的。最后基于三轴膨胀试验数据，建立了考虑应力、含水量双因素的新型三维膨胀本构，如式（2）所示。

2001 年[8]，杨庆等考虑到侧限膨胀轴向应力σz是决定性因素，对该本构关系进行了修正，将式（2）中1nσV用1nσz代替，如式（3）所示。

两式中：ω 为吸水率；A、B、C 为与岩石本身特性有关的系数。

刘晓丽等[9]（2006 年）考虑到岩石吸水后的非稳定膨胀过程，修正了Huder-Amberg 膨胀本构模型，建立了侧限条件下岩石浸水后轴向非稳定膨胀本构关系，如式（4）所示。

式中：ε∞为岩石轴向最终膨胀率；k 为岩石的吸水膨胀系数。

左清军等[10]（2016 年）考虑了初始膨胀应力的影响，修正了膨胀应力和轴向膨胀率之间的关系并进一步将σ=0.1MPa 时的轴向膨胀率K 扩展为任意t 时刻的轴向膨胀率，如式（5）所示。

综上，基于Huder-Amberg 的此类本构模型都是基于特定试验，来建立膨胀岩本构模型。这种方式决定了该种本构模型具有明显的弊端。在试验模型框架前提下构建出来的本构模型在使用时必然会受框架的限制。而工程实际通常复杂多变，便导致在运用于实际工程时理论与实际往往大相径庭。

1.2 基于湿度应力场理论

1993 年，缪协兴等[1]受温度应力场的启发，将温度应力场理论中由于温度变化引起的物性关系与岩石受水作用后的膨胀和软化物性关系进行类比，进一步将由于水渗透引起的湿度变化场代替由于热传导造成的温度变化场，提出了膨胀岩受水作用的湿度应力场理论，并提出了湿度应力场理论的控制方程。1995 年[11]，缪协兴再次提出不考虑孔隙水压力作用下，湿度应力场的平衡微分方程，如式（6）所示。

式中，ρ 为岩体的质量密度；σij为总应力分量；θ 为单位体积的含水量；E 为弹性模量；μ 为泊松比；α 为线膨胀系数。

朱珍德等[12]（2004 年）在此基础上，增加了塑性状态的本构关系，最终建立了基于湿度应力场理论的膨胀岩弹塑性本构关系，并利用参变量变分原理，给出了处理这类问题的数值变分原理与方法。任松等[13]（2018 年）基于湿度应力场理论，考虑膨胀性的时变特征，建立含时间效应的隧道硬石膏围岩的膨胀本构模型，如式（7）：

式中：Ee代替E 为弹性模量，Es为膨胀模量，t 为时间，wi为岩石初始含水量，α 为线膨胀系数，wm为岩石饱和含水量，a 为与岩石吸水性能有关的系数。

丁秀丽等[14]（2021 年）通过湿度场分析，将岩石膨胀过程分为吸湿和膨胀两个阶段，以此建立了基于吸湿-膨胀岩石膨胀变形演化模型，如式（8）。

式中：εij为应变分量，σij为应力分量，Δw 为吸湿增量，δij为Kronecker 符号。吸湿膨胀系数α 忽略吸湿效应对其影响，假定为常数。

湿度应力场理论具有严谨的数学、力学基础，但是其本身仍是建立在多种严苛假设前提下：例如不考虑温度的影响、应变和湿度的变化不能太大、固体相的变形是弹性变形和忽略流体对固体相产生的耗散过程[15]。上述研究均是根据试验结果，并结合理想吸湿-膨胀分析模型等假设得到的初步结果。基于湿度应力场的本构模型确定了一种理想物质模型，是反映工程实际材料的理想化形式，其模型正确性与否仍需后续更深入地探讨研究。

1.3 基于流变理论

第三种研究思路，将膨胀岩吸水膨胀过程转变为流变问题，利用流变理论建立膨胀岩湿胀本构关系。王贤能、尚岳全等[3，16]（1991 年，1997 年）将描述岩石流变变形常用的西原模型与其提出的描述岩石膨胀性能的膨胀模型相结合，得到了膨胀岩的膨胀与流变的耦合模型。Doostmohammadi R[17]指出膨胀潜势是与时间有关的复杂过程参数，钟志彬等[18]（2019 年）以川中红层典型泥岩为对象，揭示红层泥岩在浸水条件下的时效变形特性，提出了泥岩湿胀蠕变方程：

式中：ε（t）为与时间相关的膨胀应变，t 为时长，K 和η为与岩石本身物理力学性能有关的参数。

刘景宇等[19]（2021 年）在研究泥岩路基上拱问题时，将泥岩吸水膨胀过程转变为岩石流变问题，利用流变力学理论推导出基于时间效应下的泥岩湿胀本构关系。即式（10）：

式中：E 为弹性模量，η 为黏性系数，σ0为泥岩的膨胀力。

流变作为一个长期概念引入化学膨胀岩的膨胀过程有很强的指导作用。通过短期试验结果确定的本构模型参数与工程实践之间的适用性有待时间的考验。化学膨胀岩的体积膨胀随时间变化持续时间长，化学膨胀岩膨胀过程在根本上是流变过程[20]，相较于传统的湿度应力场膨胀本构模型，考虑了时间效应的湿度应力场膨胀本构模型可将膨胀问题转化为流变问题，这对实际工程中的过程模拟和过程控制具有重要工程实践意义。

2 讨论

对现有三类湿胀本构模型思路进行分析（如表1），可知各本构均有所局限，难以对膨胀机理作出统一有效的解释，这也是后续研究关注的重点。其次，膨胀岩的基本特性决定了其工程复杂性能，深入探究其膨胀内外因素，对于膨胀岩土工程地区建设有十分重要的意义。物理化学作用导致的膨胀现象都有迹可循，在尊重客观事实的前提下，多角度来解释膨胀本构模型是重要一环。膨胀岩产生膨胀，内因是源头，外因是催化剂，研究导致膨胀岩膨胀的内因与外因之间的联系，建立膨胀岩湿胀本构关系，系统分析外因对膨胀岩膨胀的引导控制作用，提前采取措施控制诱使膨胀岩膨胀的外部因素，可为保障膨胀岩地区工程的建设安全与正常运营提供强有力的支撑。总体而言，岩石膨胀机理研究是一个长期且持续的过程，需要各学科知识的交融碰撞。

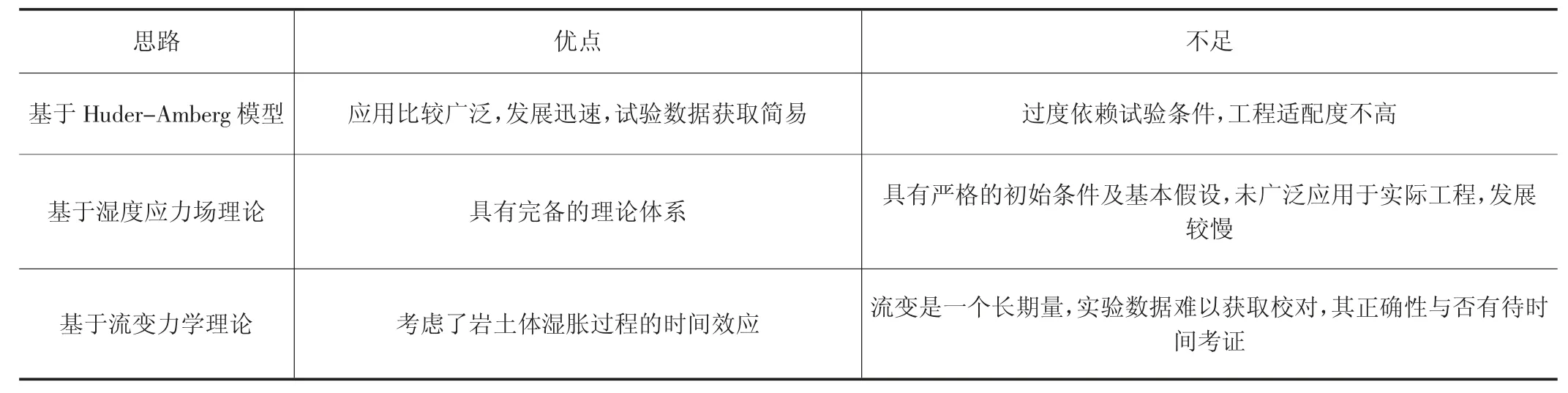
表1 现有湿胀本构研究思路对比表

3 未来研究展望

膨胀岩湿胀本构关系研究的终极目标是迎合国家战略需求，切实服务于实际工程，解决膨胀岩地区工程建设及运营过程中遇到的工程设计、施工及支护难题。因此未来膨胀岩湿胀本构关系的研究，应立足根本，长远谋划，从膨胀岩自身组构出发，考虑内因与外因共同作用，针对性的开展研究。具体而言，未来膨胀岩湿胀本构研究还需进行以下方面完善：

①应从矿物材料本身的遇水膨胀特性出发，区别黏土类膨胀岩与化学类膨胀岩膨胀机理的差异；从晶体结构出发，分析不同矿物晶体结构遇水后的物理化学反应过程，结合矿物材料细观检测及数值模拟分析技术，复现膨胀岩吸水膨胀过程，从微细观甚至纳米级层面，分析膨胀岩湿胀机理。

②国内外对于膨胀岩湿胀本构的研究，多针对完整岩样，而未考虑岩样初始状态。然而，天然状态下，膨胀岩处于一定的应力条件和水环境条件下，当未对其进行扰动时，处于稳定状态。但工程建设过程中，一旦受到施工扰动，原有的应力平衡和赋水环境将被打破，造成膨胀岩内部微裂纹扩展、贯通，新裂纹萌生，岩体结构破坏，为水的渗入提供方便，激活内部矿物膨胀潜势。因此对于湿胀本构的研究还需考虑施工对膨胀岩结构造成的损伤，研究不同初始损伤程度下膨胀岩湿胀特性的变化。

③不同类型的工程，其实际运行条件并不相同，比如输水隧洞，水压将对膨胀岩应力状态产生影响；高铁路基，运行期列车动荷载对膨胀岩内部微细观结构也有较大影响；开挖路堑，开挖深度及车辆荷载也对边坡应力场也会产生影响。因此，应与实际工程相结合，针对不同的工程岩体，考虑膨胀岩赋存环境条件，厘清膨胀岩膨胀的内外因，对比分析监测数据，完善室内理论分析模型及数值模拟方法。