墙-土耦合作用下马銮西站基坑地下连续墙开裂分析

王少卿 WANG Shao-qing；许立 XU Li；杜丽辉 DU Li-hui

（苏交科集团股份有限公司，南京 211100）

0 引言

随着我国城市轨道交通的发展，地铁站基坑的开挖深度越来越大，地下连续墙作为地铁车站深基坑最常用的支护结构，其整体质量不仅会影响施工过程中基坑的安全，也会影响后期车站的运营。

地铁站施工过程中，由于各种支护结构尚未完成，在开挖卸荷、施工荷载、地下水等多方面的综合作用下，地下连续墙常常会发生较大的变形，有时甚至会开裂而造成各种工程事故。在影响连续墙变形的各种因素中，墙后的土体的作用是主要因素，土压力的作用支护结构的破坏已经引起工程界的高度重视并开展了大量的研究。

然后，传统的分析方法主要借助经典的土压力理论，将土压力视为外荷载施加在支护结构上，其主要缺陷是未考虑土和结构之间的耦合作用，事实上，土和支护结构的耦合作用是引起支护结构破坏的主要因素。

本文以马銮西站基坑开挖为工程背景，基于土与机构相互作用理论，结合现场监测数据，采用数值模拟的方法研究了该地铁站开挖过程中地下连续墙的变形发展直至开裂的过程，分析了墙-土耦合作用下地下连续墙的开裂机理。

1 墙-土耦合的接触面单元

地下连续墙和周围土体的耦合作用是高度非线性问题，合理的接触面单元是成功的模拟的关键，针对这一问题，目前已经发展出了基于接触力学的接触面单元、剪切界面单元和薄层实体单元等多种单元。其中，Goodman 于1968 年用刚度系数与节点相对位移的线性关系表征岩石节理和断层的非连续变形机理，由此提出的零厚度接触面单元（Goodman 单元）是一种典型的薄层单元[1]。它的接触面取法向刚度与切向刚度ks及kt为主要参数。Goodman单元概念清楚，方便易行，能较好地模拟接触面的错动、滑移和开裂，因此在工程上得到了广泛的应用。

接触面切向应力应变关系采用Ciough 和Duncan 提出的应变硬化的双曲线模型[2、3]：

式中，K1、K2、Rf、n 为由试验确定的非线性指标；δ 为接触面摩擦角；γw为水的容重；Pa为大气压力。

2 计算模型及材料参数

2.1 工程概况

厦门市轨道交通2 号线，马銮西站位于规划芸湾路与鼎政路交叉路口。马銮西站主体基坑长378.45m，标准段宽47.2m，基坑深度7.81～9.20m。主体围护结构采用800mm 厚地下连续墙+1 道内支撑体系，第一道支撑为钢筋混凝土支撑，间距8～9m；盾构井采用钢筋混凝土斜支撑，间距4～6m。基坑中间设置两排临时立柱，临时立柱桩基础采用Ø1200mm 的钻孔灌注桩兼做抗拔桩，临时立柱采用4L160×16 钢格构柱。

根据工程地质调查及钻孔揭露，马銮西站地层范围内地质情况如下所示：素填土，主要由黏性土（局部夹少量碎石）等回填而成，钻探揭示层厚1.10～4.20m；粉质黏土，主要由粉、黏粒组成，钻探揭示层厚为1.20～4.60m；中粗砂以次圆状石英质中、粗砂为主，揭示厚度为1.0～3.50m；淤泥主要由黏、粉粒组成，揭露厚度1.10～5.30m，工程性能不良；粉质黏土主要由粉、黏粒组成，揭示层厚0.50～6.50m；粉细砂以次圆状石英质粉、细砂为主，揭示厚度为1.70～2.30m；中粗砂以次圆状石英质中、粗砂为主，揭示厚度为1.10～8.20m；凝灰熔岩残积黏性土为凝灰熔岩风化产物，成分主要由火山碎屑物等风化的黏、粉粒及石英组成，揭示层厚为2.60～7.70m。

2.2 计算模型

采用ABAQUS 软件建立了基坑的有限元模型（如图1），模型共12276 个节点，11868 个CPE4R 四边形单元，连续墙与周围土体之间设置Goodman 单元进行连接，各支撑与墙体采用绑定约束。

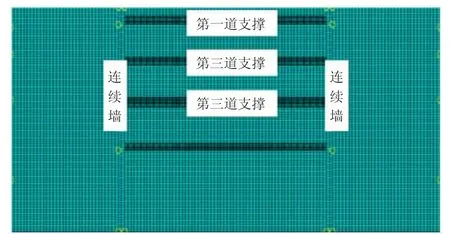
图1 计算模型（开挖前）

2.3 材料参数

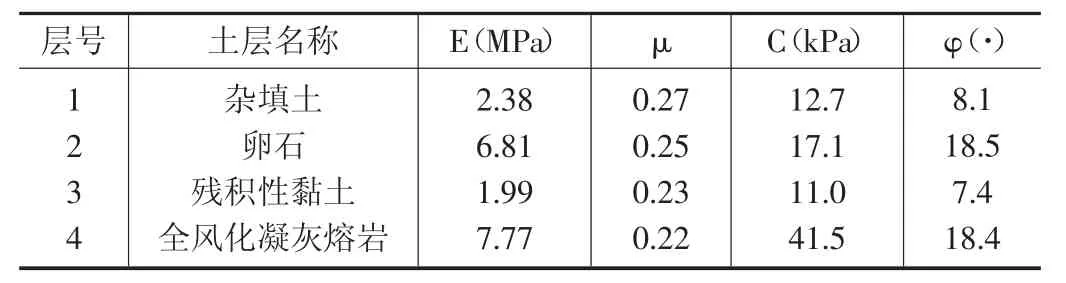
模拟中采用的土体材料采用摩尔-库伦模型，参数如表1 所示。

为模拟开挖卸荷过程中地下连续墙的开裂过程，对于连续墙的混凝土，采用ABAQUS 提供的混凝土损伤塑性模型（CDP 模型），在弹性阶段，该模型采用线弹性模型对材料的力学性能进行描述，进入损伤阶段后，CDP 模型损伤后的弹性模量可以表示为损伤因子d 和初始无损弹性模量的关系式为[4]：

式中，E0为无损伤时的初始弹性模量，d 为损伤因子，且可采用式（4）计算：

式中，t、c 分别代表拉伸和压缩；β 为塑性应变与非弹性应变的比例系数，受压时取0.35～0.7，受拉时取0.5～0.95；εin为与dk对应的非弹性应变。

本工程中，地下连续墙采用的混凝土等级为C30，初始弹性模量E0=21.1GPa，泊松比μ=0.2，材料进入塑性后，CDP 模型的应力-非弹性应变关系及损伤因子-非弹性应变关系如表2 所示。

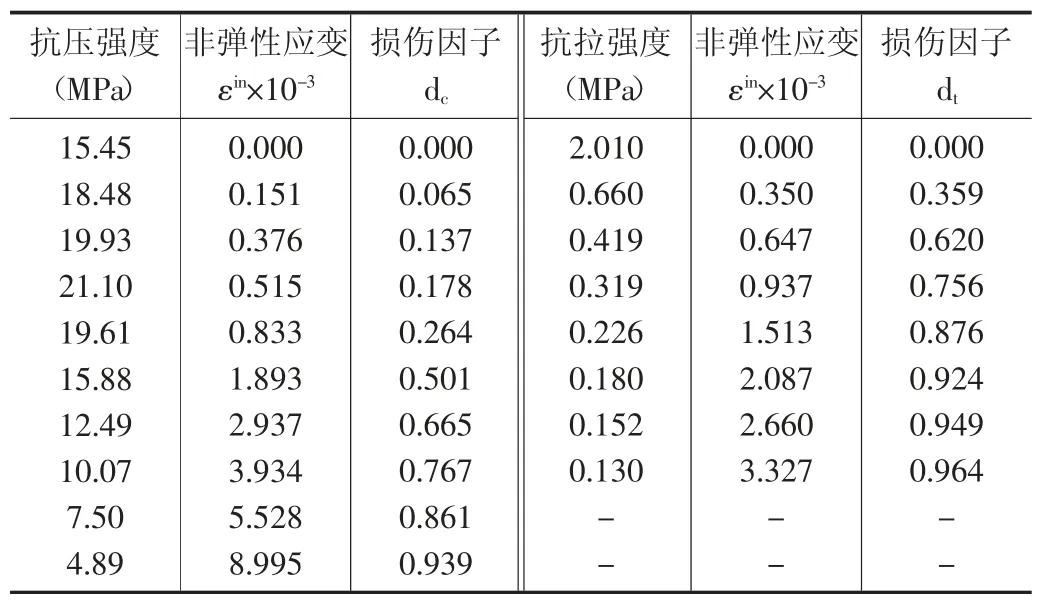
表2 地下连续墙混凝土损伤因子

桩土接触界面Goodman 单元参数如表3 所示。[5]

表3 桩土接触界面Goodman 单元参数

3 开挖过程模拟

3.1 开挖方案

模拟的主要开挖步骤如下：①小里程端头井开挖，开挖深度为2.1m，加第一道混凝土支撑；②第二层土开挖，开挖深度为5.1m，加第二道钢支撑；③第三层开挖，开挖深度为5.2m，加第三道混凝土支撑。

3.2 地下连续墙整体变形特性

模拟了开挖过程中，随着开挖深度的增加，地下连续墙的侧向情况。施工过程中，同时布置了测斜管对侧向位移进行了监测，图2 为开挖完第三层并第三道混凝土支撑后，地下连续墙的侧向位移计算值与监测值的对比，从图中可以看出，开完第三步后，地下连续墙向坑内的最大侧向位移可达27mm，位移的计算值与监测值吻合，验证了本文计算模型和方法的有效性。

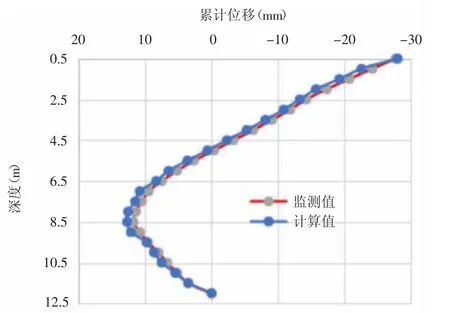
图2 墙体侧向位移计算值与监测值对比

图3 为不同开挖步下墙体的累计侧移情况，从图3 中可以看出，墙体最大水平位移发生在墙顶处，各开挖步下的累积水平位移分别为8mm、27mm 和57mm，方向为指向坑内。由于第二道钢支撑的刚度较大，第二道支撑处的水平位移较小，第二道支撑以下的墙体产生向坑外的挠曲变形，最大挠度发生在8.5m 深度处，各开挖步下的挠度值分别为1.6mm、10.8mm 和14.7mm。最大的挠度处同时也为弯矩最大值所在位置，外侧墙体混凝土易发生拉伸开裂。

图3 不同工况下墙体的侧向位移

3.3 挡土墙应力变化规律

图4 为不同开挖步下连续墙的最大压应力的变化图，从图中可以看出，随着开挖深度的增加，挡土墙的最大压力逐渐增大，各开挖步下的最大压应力分别为2.5MPa、2.8MPa和3.1MPa，对比表2 中的数据，整个开挖过程中，墙体混凝土未达到损伤临界值（15.5MPa），挡土墙未发生受压损伤。

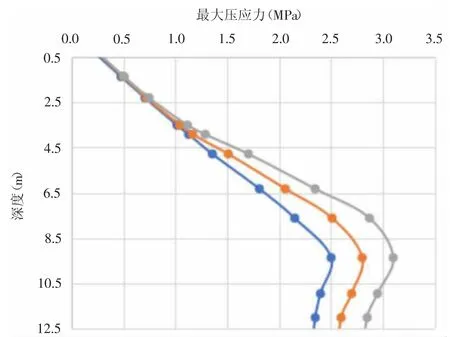
图4 不同开挖步下连续墙的最大压应力

图5 为不同开挖步下挡土墙的最大拉应力的变化云图，从图中可以看出，随着开挖深度的增加，挡土墙的最大拉力逐渐增大，各开挖步下的最大压应力分别为0.34MPa、0.72MPa 和1.08MPa，提取了不同深度处的最大拉应力，得到各开挖步下最大拉应力随着深度的变化关系，从图中可以看出，深度为8.1m 处的墙体，在第二开挖步时，最大拉应力可达0.72MPa，超出表2 中的混凝土材料的临界损伤压力，随着开挖深度的增加，该点处的非线性变形逐渐增大，损伤因子逐渐增大，墙体出现开裂。图6为8m 深度处墙体开裂的现场照片，实际开裂位置与计算的开裂点位置基本吻合。地下连墙主拉应力主要是由于坑内支撑较少，墙体在坑外土压力的作用下，产生向坑内的挠曲变形，在最大弯矩处，坑内侧强度的最大拉应力超出混凝土材料的损伤起始应力，随着开挖深度的增加，该点处的非线性位移逐渐增大，直至墙体产生开裂。为避免墙体开裂，工程中需要调整肯定支撑的位置、增加支撑数量或者提高支撑的刚度以降低墙体的峰值弯矩，避免墙体开裂。

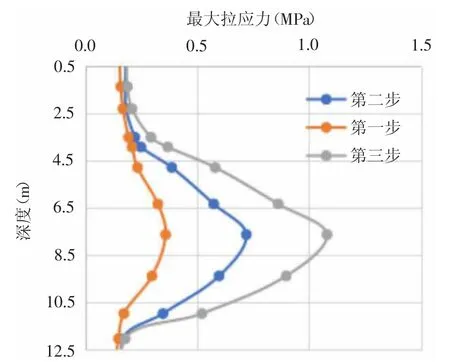
图5 不同开挖步下连续墙的最大拉应力

图6 墙体开裂实测图

4 结论

①墙体水平位移整体为鼓胀型变形，呈现“两头小、中间大”的趋势。地下连续墙整体变形在控制范围内，超过临界值的仅占1%；基坑墙顶外侧变形和内侧变形的比例分别为62.5%和37.5%。②地下连墙主拉应力主要是由于坑内支撑较少，墙体在坑外土压力的作用下，产生向坑内的挠曲变形，在最大弯矩处，坑内侧强度的最大拉应力超出混凝土材料的损伤起始应力，随着开挖深度的增加，该点处的非线性位移逐渐增大，直至墙体产生开裂。③在墙-土耦合作用下，同类型的基坑应避免此种只有地表一道支撑的情况，避免出现地下连续墙开裂甚至基坑倾覆的险情。