基于GNSS 的长江下游带状区域高程拟合方法研究——二次多项式与BP 神经网络的对比分析

高 尚，金 犇，郭 凯

（长江水利委员会水文局长江下游水文水资源勘测局，南京 210011）

在长江沿线的基础测绘和工程建设中，高程数据是必不可少的。传统的高程测量方法，如几何水准法，虽然准确，但在大范围水准测量中成本高且效率低下[1]。随着卫星导航定位技术的发展，GNSS（全球导航卫星系统）高程在工程测绘中得到广泛应用。然而，由于卫星定位技术所采用的高程基准面是参考椭球面而非传统水准基准的大地水准面，导致出现高程异常问题。为解决高程异常影响，研究者们提出了多种方法，包括曲线拟合模型、曲面拟合模型、神经网络模型和地球重力场模型等。

其中，二次多项式方法作为曲面拟合模型在高程拟合中得到广泛应用。该方法通过最小二乘准则构建拟合方程，并利用此方程外推高程异常值。粟剑[2]采用曲线拟合法将GNSS 大地高转换为正常高，使拟合高程达到三等测量精度。唐诗华等[3]针对GPS 高程拟合方法的精度问题，根据测量实例比较了各种最小二乘法的拟合能力。研究表明：最小二乘估计在高程拟合中精度最高。张腾旭等[4]通过研究发现对于大面积高程异常值变化较大的地区，最小二乘配置法能够取得较高的拟合精度。在高程拟合方面，张潘等[5]通过高程拟合与三等水准测量成果进行对比分析，验证了模型在实际中应用的优越性。

近年来，随着机器学习算法的不断发展，如BP 神经网络，采用机器学习来进行高程异常拟合也引起了许多学者的广泛关注。曾凯等[6]利用神经网络进行高程拟合应用。邓才林等[7]采用BP 神经网络对湖南省新化县进行高程异常拟合。李林晓等[8]对改进的RBF 神经网络组合模型中的关键参数进行优化选取，且应用于工程实践中。

本文旨在探究二次多项式拟合和BP 神经网络在高程拟合中的应用。通过评估内外符合精度，对比分析2 种方法的精度表现。该研究将提供一种新的解决方案和方法，为长江沿线大范围带状区域的高程拟合问题提供支持，以提高测绘和工程建设的精确性。

1 拟合方法

1.1 二次多项式曲面拟合

高程异常的多项式拟合法就是建立一个以二维位置参数为自变量的多项式函数模型，其函数值即为高程异常，通过一定数量的已知点的高程异常值可计算出多项式的系数。对于公共点（同时具有大地高和正常高的点）上的高程异常与平面坐标之间假定有如下数学关系

式中：ξi为对应于平面坐标（xi，yi）的高程异常，a0、a1、a2、a3、a4、a5为所求的模型参数，εi是误差，因此，需要6 个或6 个以上公共点，采用最小二乘原理进行数学模拟，确定模型。

将式（2）写成矩阵形式

通过列以上的方程并解算，本文可以求出各个重合点的正常高。具体方法是，解出在Σε2=min 条件下的ai值，再通过公式（2）求解出未知点的ξ。

1.2 BP 神经网络拟合

BP 神经网络也可以称为多层前馈型神经网络，其最大特点是信号和错误的反向传输。初始权重是随机设置的，然后根据反向传播过程中训练数据（训练过程中的计算值）与输出数据（训练要达到的实际值）之间的差异进行修改。重复前进和后退过程，直到训练数据和输出数据之间的差异达到训练精度为止，其具体网络结构如图1 所示[9]。

图1 BP 神经网络模型算法结构

BP 神经网络由输入层、隐含层和输出层三部分组成。设神经网络的输入向量为X=（X1，…，Xn）T，期望输出为d=（d1，…，dm）T，输入层与隐含层的权值矩阵为V=（v1，v2，…，vk，…，vq）T，阀值为θ，隐含层和输出层的权值矩阵为W=（w1，w2，…，wi，…，wm）T，神经网络的正向传输的计算过程如下。

隐含层的输出计算公式为

输出层的输出计算公式为

式中：f1（I1）、f2（I2）为隐含层与输出层的传递函数，f1（I1）通常为Sigmoid 函数。f2（I2）可以为Sigmoid 函数或Purelin 函数，y2为最终的输出值。

常用BP 神经网络通常采用误差反向传播法调整连接权。神经网络的目标函数为

式中：p 表示第p 个样本，k 表示第k 个节点，dk表示期望输出。

本文的BP 神经网络简述如下：使用MATLAB神经网络工具箱建立，输入层包含高程点平面坐标x 和y，输出层为高程异常。训练函数选用了tansig、purelin 和trainlm，训练参数设置net.tranParam.show=100，net.tranParam.epochs=1000，net.tranParam.lr=0.01，net.tranParam.goal=le-3，并且其他参数采用MATLAB神经网络工具箱默认值。

2 实例分析

2.1 实例数据来源

南京河段是长江中下游重点河段之一，上承马鞍山河段，下接镇扬河段。河段起始端和尚港是苏皖两省分界点，终端为泗源沟，主泓长100.3 km。本文采用长江下游安徽马鞍山市小黄洲沿江至江苏镇江市世业洲头的E 级GNSS 控制点作为样本数据，该段区域控制点共有71 个，控制长度约为104 km，控制点呈带状分布在长江两岸沿线（点位分布图如图2 所示），水准高程按照三等水准测量要求施测。本文取60 个分布相对均匀的点作为样本点，11 个点作为待拟合点。

图2 点位分布图

2.2 精度评定

为了分析不同模型的可塑性，可以使用已知点的GNSS 高程异常值与拟合的高程异常值进行比较，并定义拟合残差，来验证不同模型的精度。精度评定分为内符合精度和外符合精度。

2.2.1 内符合精度

根据参与拟合计算已知点的GNSS 高程异常值ξi与拟合的高程异常值进行比较，并用来定义拟合残差，内符合精度μ1公式如下所示

2.2.2 外符合精度

根据参与拟合计算检核点的GNSS 高程异常值ξi与拟合的高程异常值进行比较，并用ui=ξi-ζi′来定义拟合残差，外符合精度公式如下所示

2.3 拟合结果分析

分别采用2 种方式对测区范围内的60 个高程值进行拟合，验证精度的误差最大值（max）、误差最小值（min）、均方根误差（RMS）、平均绝对误差（MAE）、中误差见表1，2 种方法在对应点拟合残差如图3 所示，BP神经网络拟合结果如图4 所示。

表1 内符合精度对比

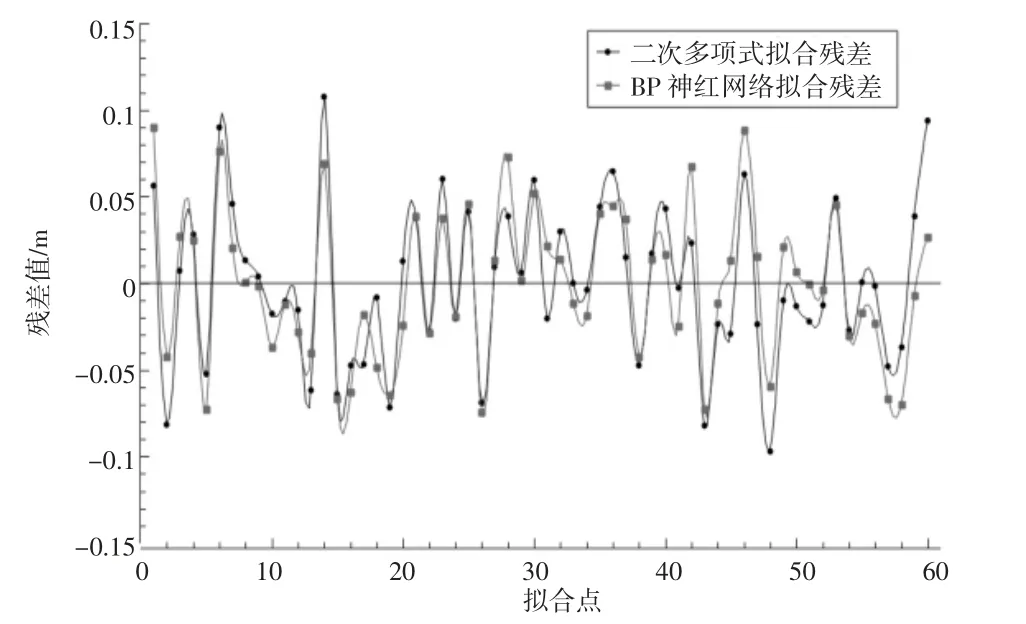
图3 二次多项式与BP 神经网络拟合残差

从表1 与图3 中可知，采用2 种拟合方式都有较好的拟合效果，计算结果非常接近，误差趋势也一致。

通过对2 种拟合方式的数据进行对比，可以看出，在该测区范围内，通过二次多项式和BP 神经网络2 种拟合方式计算得出的结果相差较小。针对11 个均匀分布的校核点进行外符合精度计算比较，得出以下结论：

首先，从表2 中可以看出，2 种拟合方式在最大值和最小值方面的绝对值误差都在测量要求范围之内。

表2 外符合精度对比

其次，通过比较RMS 和MAE，可以看出2 种拟合方式在整体预测精度上也相差较小。RMS 和MAE 都是衡量预测结果与真实值之间误差的指标，数值越小代表预测的精度越高。根据表2 中的数据，二次多项式的RMS 为0.040 4，BP 神经网络的RMS 为0.034 5，这说明使用BP 神经网络进行拟合的结果相对更加精确。而在MAE 方面，二次多项式的数值为0.033 1，BP 神经网络的数值为0.025 3，也表明了BP 神经网络相对于二次多项式更能接近真实数据。

最后，本研究还可以观察比较2 种拟合方式的中误差。中误差是用来衡量预测值的分散程度，数值越小说明预测结果的稳定性越好。根据表2 的数据，二次多项式的中误差为0.042 3，BP 神经网络的中误差为0.036 2，可以看出2 种拟合方式在中误差上也存在一定的差距，BP 神经网络的结果更加稳定。

综上所述，通过对2 种数据拟合方式进行比较，研究可以得出结论：无论是二次多项式还是BP 神经网络，都能够满足测量要求内的误差，并且2 种方式的预测结果相差较小。在整体预测精度上，BP 神经网络相对于二次多项式表现更佳，其RMS 和MAE 的数值较小，能够更准确地拟合真实数据。此外，BP 神经网络还表现出更好的稳定性，其中误差较小。因此，本研究可以认为BP 神经网络是一种更适用于该测区范围内数据对比的拟合方式。

3 结论

本文以长江下游马鞍山至镇江多项式段布设的E级GNSS 控制网作为实验区域，使用二次多项式曲面拟合、BP 神经网络拟合2 种常用的方式进行高程拟合，对大范围带状区域高程拟合方法进行研究。通过研究得出：

1）确定地球表面高程异常的大小不仅与地球内部的密度变化有关，也与地形起伏等多种因素有关。因此，对于给定区域内的高程异常点，采用一种数学函数进行拟合时，由于拟合模型的缺陷，必然存在误差。在选择拟合方程来描述高程异常分布时，只能选择误差相对较小的模型，这是比较合理的做法。

2）已知点的分布情况对拟合效果和选择拟合模型具有关键影响。如果已知点覆盖整个拟合区域，则拟合精度通常比较稳定。但是，如果待拟合的点位于已知点所涵盖的区域之外，则拟合精度会降低。

3）2 种高程拟合方法相对比，BP 神经网络拟合具有相对更好的拟合结果，但容易陷入局部最优解，应在实际应用当中，多次进行训练，最后选择更好的拟合结果。

综上所述，在长江下游平原沿线区域，进行高程拟合时，可采用BP 神经网络拟合法。