基于超声导波反演参数定征皮质骨骨质状况研究
2024-01-17盛帆宋小军樊天地张璠李义方
盛帆,宋小军,2,樊天地,张璠,李义方
(1.上海电力大学电子与信息工程学院,上海 201300;2.复旦大学生物医学工程中心,上海 200433;3.国网安徽省电力有限公司超高压分公司,安徽合肥 230000;4.复旦大学工程与应用技术研究院,上海 200433)
0 引言
随着人口老龄化的加剧,与衰老密切相关的骨质疏松越发引起人们的关注。当发生骨质疏松时,骨质将会减少,骨孔隙度增大,骨折风险增加[1]。目前骨质疏松的主要检查手段有双能X射线吸收法(DXA)[2]、计算机断层扫描技术(CT)[3]。与之相比,定量超声法具有无辐射、穿透力强、费用低、便携等优点[4-5],在骨质疏松检测中具有良好的应用前景。
轴向透射(AT)技术已被用于评估皮质骨[6]。AT技术可以从皮质骨采集到两种超声信号。一种是第一到达波信号(FAS),另一种是超声导波(UWG)[7]。FAS对应的超声波沿皮质骨表面传播,而UWG则在整个皮质骨层传播,对骨微观结构更为敏感[8-9]。
Patrick 等[10]在Lamb 波中提取了对皮质骨厚度较敏感的A0 模式,并成功反演出了皮质骨厚度。Daniel Pereira等[11]在低频超声下(<60 kHz)对5具尸体桡骨(年龄53~88岁)进行研究,成功反演出密度、厚度、外径和形状因子(SF)。Tran等[12]开发了一种基于网格搜索算法的反演程序获得了单层骨板的皮质骨厚度和体波速度。Li等[13]设计一种卷积神经网络算法,搭建皮质骨参数和超声导波之间的映射关系,成功反演了牛皮质骨厚度、纵波速度和横波速度。
以上研究成功反演出了皮质骨厚度等参数,但并未对皮质骨参数和骨质疏松相关性展开研究。本文利用有限元方法构建不同孔隙度的皮质骨模型来模拟不同程度的骨质疏松,并利用Floquet-Bloch理论搭建理论频散曲线数据库,通过反演算法获得皮质骨厚度,横波速度和纵波速度参数,以研究骨质疏松与皮质骨参数之间的定量关系。最后,进行离体牛胫骨实验验证了反演算法的合理性。
1 理论与方法
1.1 皮质骨中的兰姆波
兰姆波(Lamb)是一种常见的在自由边界固定板(或层)中传播的超声导波,具有频散性和多模态性[14-15]。当超声波在自由板中传播时,波在板的边界发生多次反射与转换,横波纵波之间相互干扰,最终形成稳定的波包,即不同模式的兰姆波。对于厚度为2d的自由板,不同的导波组合成的多模式频散曲线可由Rayleigh-Lamb[16]方程得出,对称模式时:
反对称模式时:
式中:k是波数,k=ω/Vp;Vp是Lamb波的相速度;ω是角频率;系数p和q由式(3)给出;VL和VT分别是纵波速度和横波速度。波数和频率的关系曲线即频散曲线,可通过求解方程式(1)和式(2)获得。
1.2 时域信号处理及频散曲线提取
为了利用超声导波反演皮质骨厚度、纵波速度和横波速度,需要从采集到的超声信号g(x,t)中提取仿真实验和离体实验的频散数据。使用二维傅里叶变换(2D-FT)将采集到的时间t和空间x域的超声信号g(x,t)转换为频率ω和波数k域。模态能量的分布H(ω,k)即相应的频散轨迹,H(ω,k)的表达式为
二维傅里叶变换方法容易受到噪声和频率混叠的影响,特别是在离体实验中,由于受到探头尺寸、数量以及测量范围的影响,致使离体数据波数域的分辨率相对较低。为了提高波数域的分辨率,本文用Burg 算法获得更高分辨率的ω-k域频散数据[17]。
1.3 理论频散曲线与数据库
Floquet-Bloch理论已应用在不同结构的超声频散特性分析中[18],相较于传统理论频散曲线计算的谱方法,具有建模简单,计算简单,频散曲线模式较多的优点[19]。二维无限长板可以近似看作沿x轴方向上周期为L的周期性结构。Floquet-Bloch理论实际在计算单元两侧应用周期性边界条件模拟无限长波导,将无限长薄板简化为微单元进行计算,以达到简化建模和计算的目的,表达式为
式中:usrc和udst是源边界和终点边界的位移;rsrc和rdst是源边界和终点边界的坐标。对于微小的单元模型,在给定的波数k下,计算出对应的特征频率f,得到k-f数据对,作为理论频散曲线的原始数据。理论频散曲线数据库在参数预设范围内,按照设定的增量步长,从预设范围内的最小值逐步增大到最大值。理论频散曲线数据库规格如下:皮质骨厚度h的范围为2~5 mm,增量步长为0.5 mm,纵波速度VL的范围为3 300~4 200 m·s-1,增量步长为50 m·s-1,横波速度VT范围为1 500~2 500 m·s-1,增量步长为25 m·s-1。
1.4 反演算法
经过2D-FT 和Burg 算法处理后,实验频谱能量将保存在二维矩阵A中,具体表述为
式中:m和n分别是频率和波数的范围;aij是(i,j)点对应的能量值;理论频散曲线在波数域和频域可以表示为矩阵B:
如果理论频散曲线经过点(i,j),则bij=1,如果理论频散曲线不经过点(i,j),则bij=0。
非线性目标函数J的表达式为

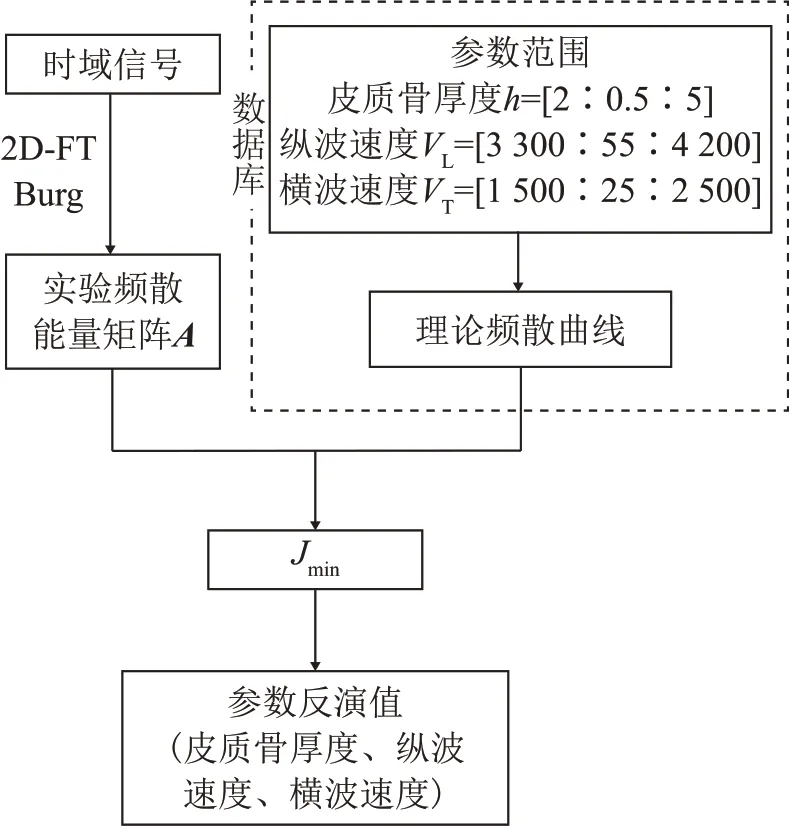
图1 参数反演流程图Fig.1 Flow chart of parameter inversion
2 仿真与实验
2.1 仿真实验
本文以有限元法为基础,通过仿真软件COMSOL 求解偏微分方程来实现真实物理场景的仿真。选择固体力学模块和压力声学模块中的时域求解器,建立二维仿真模型,如图2所示,中间为带孔皮质骨,长度为50 mm,为简单起见,将孔隙设为均匀分布,孔隙度范围设置为0~27%,间隔3%,共10组,用以模拟不同程度的骨质疏松。完美匹配层(Perfectly Matched Layer,PML)是一种人工吸收介质,可以实现对入射波的准完美吸收,以减少边界反射,将它设置于模型的两侧。皮质骨参数设置如表1所示,与人体参数类似。

表1 皮质骨有限元仿真模型参数Table 1 Simulation model parameters for cortical bone
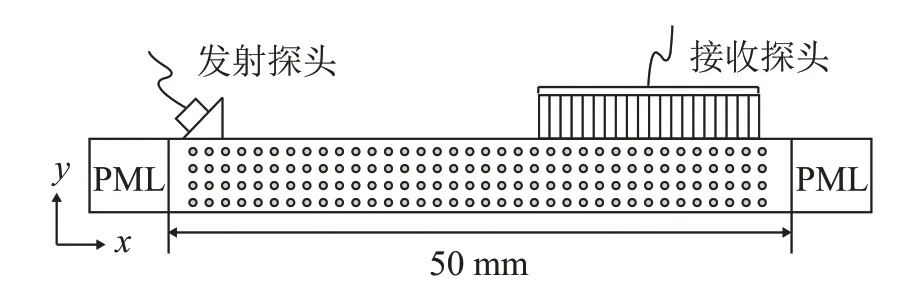
图2 皮质骨有限元仿真模型Fig.2 Simulation model of cortical bone
超声波激励由发射探头发出,入射角45°,经过楔块传入皮质骨中。激励信号中心频率过高,会导致超声信号严重衰减,激励信号中心频率过低,会使频散曲线模态较少,不利于反演,故本文采用中心频率1 MHz 的3 周期高斯包络正弦波作为激励,如图3所示,表达式为
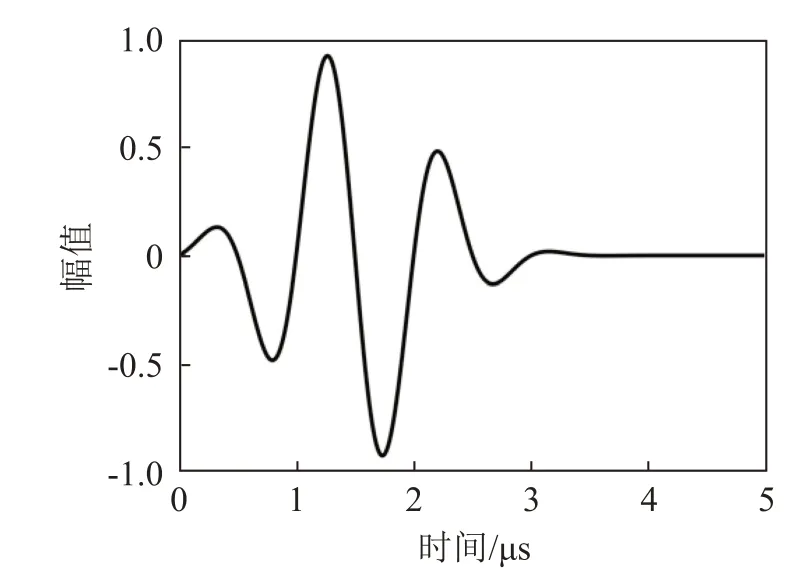
图3 激励信号波形Fig.3 Waveform of excitation signal
式中:H为信号幅值;fc为中心频率;σ为标准差,设为6×10-7;t0为中心位置,设为1.5 μs。
接收探头共60 组,相邻两组间距为0.5 mm,与皮质骨表面垂直,为确保计算的稳定性、精度和计算效率,将采样频率设为10 MHz,共采集60组轴向时域信号。网格预定义设置为极细化,最大单元为524 μm,最小单元格为3 μm。
2.2 离体实验
从市场购买6组牛胫骨,将表面软组织刮除并进行脱脂处理,用游标卡尺测量牛皮质厚度。分别为2.78、2.82、3.58、3.70、3.83 和3.92 mm。纵波速度与横波速度无法直接测出,为确保反演结果的准确性,后续会将离体实验提取的频散曲线轨迹与反演结果对应的理论频散曲线进行对比。
实验装置如图4所示,单个发射探头和多组接收探头阵列在试样表面的轴向上对齐。使用中心频率为1 MHz、直径为15 mm的外部发射探头。接收阵列是一个具有128组探头(本实验仅使用前64组)的多元件阵列。由任意波形发生器(美国)产生3 周期高斯包络正弦信号作为激励,经由功率放大器后输入到发射换能器,接收阵列连接到可编程多通道超声波实验平台,采样频率为10 MHz。发射换能器保持固定,接收阵列使用前64 个接收换能器,接收探头间距为0.5 mm,共采集64组超声数据。

图4 离体牛胫骨实验装置图Fig.4 Experimental setup diagram of the isolated bovine tibia
3 实验结果及分析
3.1 仿真实验结果分析
对于孔隙度为0的皮质骨模型,将接收到的60组超声导波信号作归一化处理,结果如图5(a)所示。其中横坐标为超声信号在发射探头和接收探头之间传导时间,纵轴依次为60 组接收探头通道编号。对60 组时域信号先后分别通过2D-FT 和Burg算法处理,得到频散数据,结果如图5(b)所示。图5中红色区间能量高,能量沿着频散轨迹向两侧递减。将频散数据与数据库中的理论频散曲线进行匹配反演,非线性目标函数的最小值Jmin所对应的皮质骨厚度、纵波速度、横波速度分别是4 mm、3 650 m·s-1、1 850 m·s-1,其中,纵波速度的相对误差为1.35%,厚度和横波速度与仿真模型的设置参数完全相同,验证了反演算法的可行性。
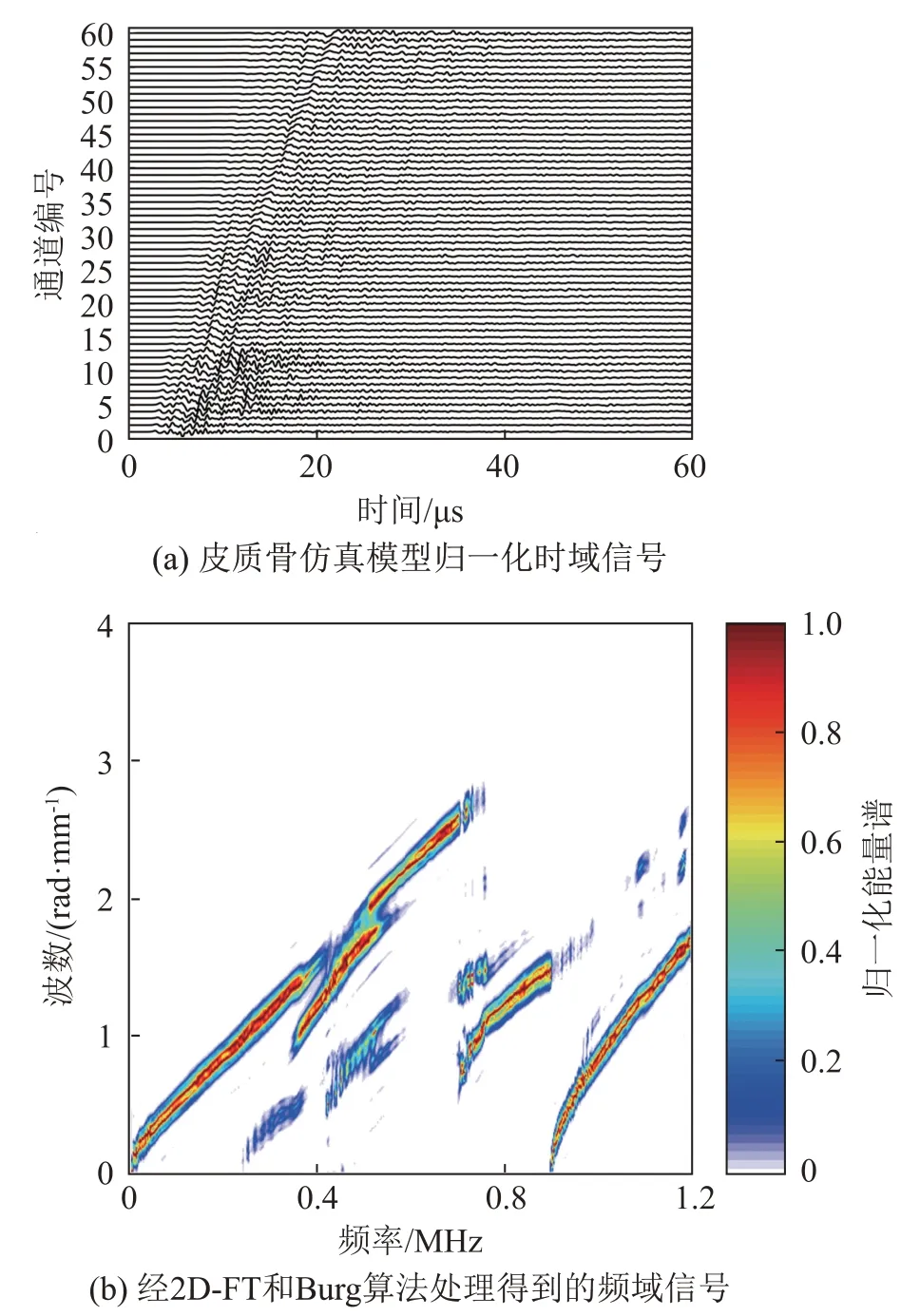
图5 皮质骨仿真模型中的时域信号和频域信号Fig.5 Time and frequency domain signals in a simulated cortical bone model
将其余9组不同孔隙度皮质骨模型的超声时域数据分别经2D-FT和Burg算法得到实验频散曲线,再利用反演算法获得皮质骨的厚度、纵波速度和横波速度。不同孔隙度皮质骨模型的反演结果如表2所示。
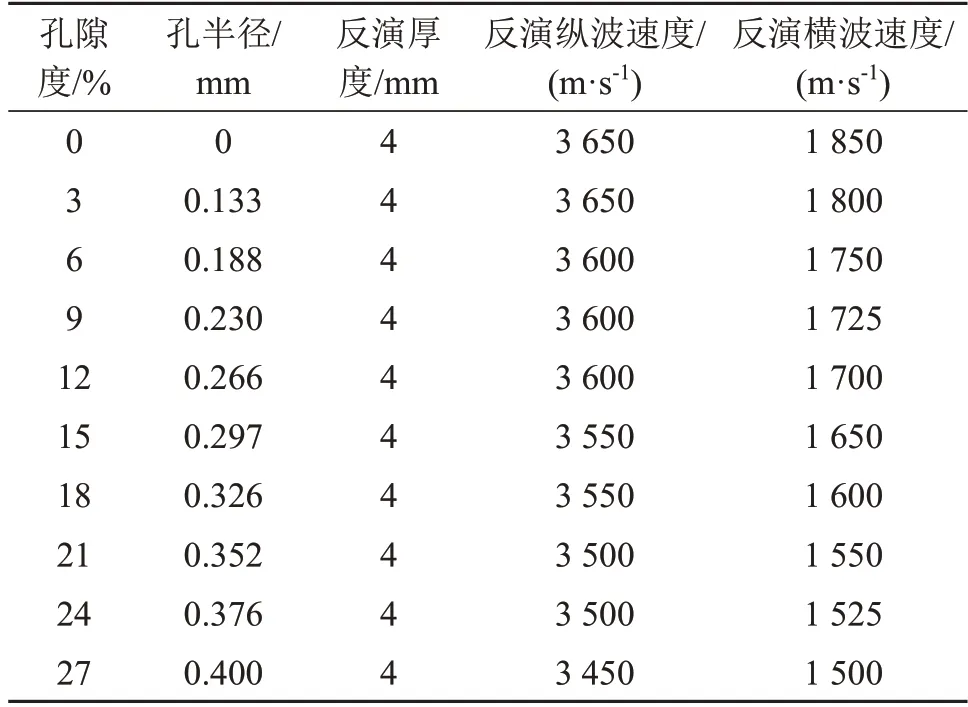
表2 不同孔隙度皮质骨模型的反演结果Table 2 Inversion results of cortical bone models with different porosities
10组不同孔隙度皮质骨模型的实验频散能量轨迹(彩色)与其反演参数理论频散曲线(黑色)的对比,前者与后者基本保持一致,如图6所示。图6(a)显示了实验频散能量轨迹(彩色)与皮质骨反演参数理论频散曲线(黑色)的对比,前者与后者相一致,进一步验证了反演算法的准确性。

图6 不同孔隙度仿真实验频散曲线与对应的理论频散曲线Fig.6 Comparison of the experimental dispersion trajectories with the corresponding theoretical dispersion curves under different porosities
当老年人患有骨质疏松时,与健康骨骼相比,其骨孔隙度将变大,这意味着其皮质层将变得多孔(充满组织液),密度降低。纵波可以在固体、液体和气体中传播,但固体中的纵波速度高于其他两种介质[20]。相比之下,横波不能在液体和气体中传播,只能在固体介质中传播。不同孔隙度下反演得到的纵波速度和横波速度如图7所示。可以看出,随着皮质骨中孔隙度的增加,反演得到的横波速度和纵波速度都随之下降,说明皮质骨的横波速度和纵波速度与骨质疏松具有较强的相关性。
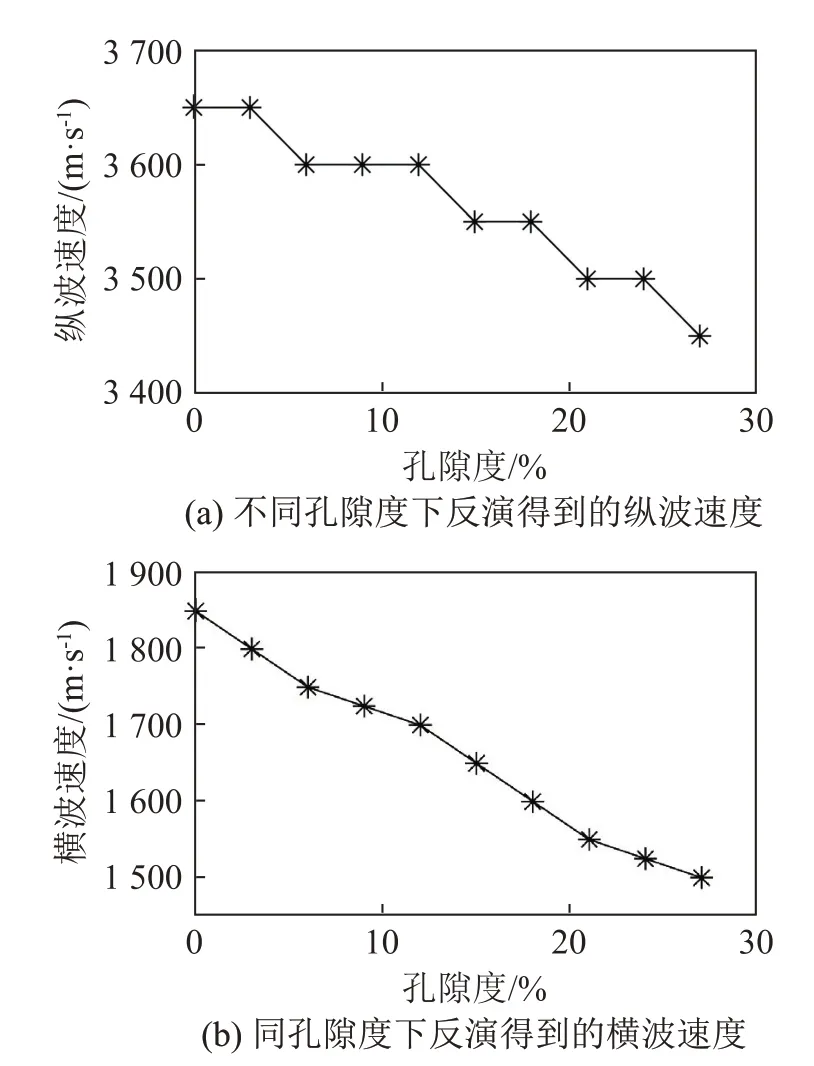
图7 孔隙度与反演的纵波和横波速度的关系Fig.7 Relationships of the inversed longitudinal and transverse velocities with porosities
为了研究皮质骨的横波速度和纵波速度与骨质疏松相关性的强弱。本文用QT、QL分别表示横波速度和纵波速度的敏感度,计算公式为
式中:VT0和VL0分别是孔隙度为0时反演得到的横波速度和纵波速度;VT27和VL27分别是孔隙度为27%时反演得到的横波速度和纵波速度。
计算得到横波速度敏感度为19.0%,纵波速度敏感度为5.5%,表明在增加相同孔隙度的情况下,横速度衰减更为明显,即横波速度对于孔隙度的变化比纵波速度更敏感。其原因可能是骨质疏松症发生时,皮质骨中被组织液填充的孔隙变大变多,纵波在孔隙中传播速度减慢,而横波不能在孔隙中传播,这也表明横波速度在骨质疏松临床诊断中的应用潜力更大。
3.2 离体实验结果分析
图8 为离体牛胫骨的64 组接收超声时域信号(皮质骨厚度为2.78 mm),每组时域信号都进行归一化处理。将此64 组时域信号经过2D-FT 和Burg算法处理后提取出频散能量。将频散能量数据与数据库中的理论频散曲线进行反演,得到Jmin所对应的皮质骨参数分别是皮质骨厚度为3 mm、纵波速度为3 950 m·s-1和横波速度为1 800 m·s-1。
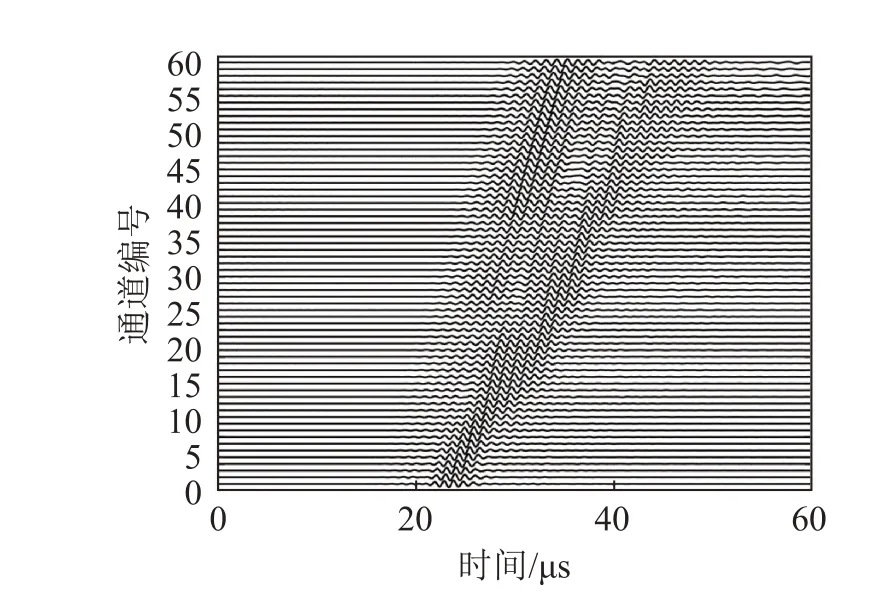
图8 离体牛胫骨实验得到的64组超声导波信号Fig.8 The 64-groups of ultrasonic guided wave signals obtained from the bovine cortical bone ex-vivo experiment
对3 组离体牛胫骨实验数据的处理结果如表3所示。由表3可知,反演得到的皮质骨厚度与其实际测量值的误差分别为7.9%,6.0%,2.2%,5.7%,4.3%,2.0%,平均相对误差4.0%。

表3 6组牛胫骨离体实验反演参数Table 3 Inversion parameters for the six sets of bovine cortical bone ex-vivo experiments
实验频散曲线(彩色)与反演参数对应的理论频散曲线(黑色)如图9所示。前者与后者吻合较好。以上结果说明本文的反演算法可以较准确地获得与骨质疏松相关的厚度参数,验证了本文算法在真实皮质骨参数反演上的可行性和准确性。
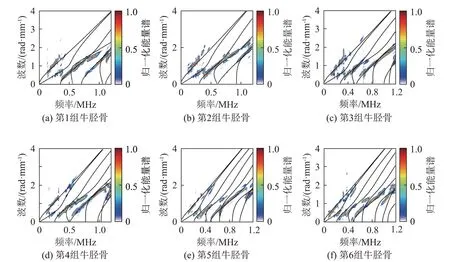
图9 牛胫骨离体实验得到的频散能量轨迹与反演参数对应的理论频散曲线对比Fig.9 Comparison of the dispersion energy trajectories obtained from the bovine cortical bone ex-vivo experiment with the corresponding theoretical dispersion curves
4 结论
针对皮质骨的骨质状况,本文提出了一种基于超声导波的反演算法,构建了不同孔隙度的皮质骨模型,利用Floquet-Bloch理论建立了单层皮质骨理论频散曲线数据库。仿真实验结果显示,随着皮质骨中孔隙度的增加,反演得到的横波速度和纵波速度都随之下降,说明皮质骨的横波速度和纵波速度与骨质疏松具有较强的相关性,且横波速度相较纵波速度更敏感,临床检测潜力更大。离体牛胫骨实验验证了本文算法在真实皮质骨参数反演上的可行性和准确性。在今后的研究中,我们将与医院合作,采集骨质疏松患者的超声导波信号,从而进一步分析皮质骨参数与人体骨质疏松的关系。
