基于混合轴辐式网络的快递运输路径再设计
2024-01-16李悦,秦威
李 悦,秦 威
(上海交通大学 工业工程与管理系,上海 200240)
相较于其他物流服务,快递运输要求有更快的速度、更低的成本、更短的时间,几乎不涉及存储功能,因此,运输网络的设计和运输路径的选择是快递公司关注的焦点。自O’kelly 等[1]提出轴辐式网络系统后,凭借其规模经济效应,该系统被广泛地应用于快递运输行业。然而随着电子商务规模的不断扩大和市场的不断下沉,小城市间快递业务量的快速上升导致了传统轴辐式运输网络中转运成本的大幅增加,快递运输需求量在地理空间上逐渐呈现高度离散化特点,直播等营销方式也使得特定需求在时间上的波动性加剧。当两个终端网点之间的快递需求量超过车辆的容量限制时,集单形成的规模经济不复存在,绕道产生的额外运输成本和中转成本降低了网络的经济性。此外,由于用户对快递时限的需求提高,转运过程的时效性也需要进行优化。本文将在轴辐式网络中加入终端网点间的连通路径,研究混合网络的创建方法,解决高度离散和波动的快递需求下规模经济效应和转运成本的平衡问题。
大部分已有的关于快递网络和运输路径优化的文献将转运中心的选址布局作为重点。曹静茹等[2]使用熵权法评价每个城市的物流发展潜力,选择对其他终端网点引力强度大的城市作为转运中心。胡志华等[3]将干线长距离运输的规模经济效应折扣系数作为考虑,建立更符合实际情况的转运中心选址模型。赵旭等[4]考虑到运输需求和成本难以预测的特点,采用极小极大值法刻画了轴辐式网络的成本函数,提出求解各方面因素不确定情况下的最优化枢纽港选择方案。杨珺等[5]考虑网络节点中断带来的延迟惩罚,建立转运中心选址的上下界模型,并使用禁忌搜索算法进行求解。李莉[6]、毕海玲等[7]、Ghaffari-Nasab 等[8]、Serper 等[9]提出多种启发式算法解决轴辐式网络转运中心的选址问题。丁伟等[10]对轴辐式运输网络在国内的应用进行了实证分析
近年来一些文献也研究了轴辐式网络结构的变形和拓展。胡晶晶等[11]为了充分利用物流资源,提出两个轴辐式网络间的协同建设,通过多层编码的遗传算法实现求解并进行了敏感性分析。Perez 等[12]尝试在多个转运中心的前提下,灵活地将终端网点分配给不同的转运中心,建立相应的数学模型并证明其有效性。Lee 等[13]设计一种包括多个终端网点、多个处理中心和一个转运中心的混合轴辐式快递网络,提高了网络结构的收敛性。姚冠新等[14]提出允许直达的混合轴辐式网络规划模型以满足城乡一体化物流需要。丁小东[15]在借助重力模型进行了流量分析后,指出我国高铁快运应采用轴辐式网络为主、点对点连通为辅的混合模式,但并未提出具体改良方法。
既有研究虽然已经在纯轴辐式快递运输的网络布局和运输路径方面取得了丰富成果,也有学者指出了未来混合式网络的发展方向,但尚未有在已有网点的基础上,将轴辐式网络和终端联通式网络相结合的具体方法。本文将在快递公司现有终端网点的基础上,研究在快递运输需求发生波动时,动态地将终端直连路径融入轴辐式网络的混合轴辐式运输方法。
1 问题描述与建模
1.1 问题描述
混合轴辐式运输网络的建立依赖于快递公司已运营一段时间的终端网点,按照每天网点间快递运输需求量的情况,动态地为每两个网点间的运输需求规划合适的中转方式和运输路径。决策包括3 个部分:1) 两两网点间的快递是否直发?2) 哪些网点被选为当天的转运中心?3) 非直发快递经哪个转运中心进行转运?决策的目标为快递运输过程的总成本最小。由于因终端网点建设产生的沉没成本以及快递在始发点和目的点的搬运和装卸成本不可避免,总成本中不再计算。总成本的环节包括在网点间进行公路运输产生的运输成本以及在转运中心进行装卸、分拣和存储产生的持货成本。公路运输由货车进行,可能发生在3 种路径上:从出发点送往转运中心、从转运中心送往目的点、在直发路径上直接从出发点送往目的点。相同起止点的快递也可以经由两辆卡车分别采用转运和直发的方式进行运输。
由于转运中心的位置每天都有可能变化,前一天聚集在转运中心的快递将不再经过转运中心间的二次转运,而是直接送往目的点,这部分快递需求将被标记为起始点为转运中心的紧急需求,与一些原本就有严格时效要求的快递合并。如果紧急需求的出发地和目的地都不是当日的转运中心,两个网点间将必须开通直发路径。紧急需求的标记使得前一天被选为转运中心的网点在次日连续被选中的可能性大大提升,也在一定程度上提升了混合轴辐式网络的稳定性。
本文假设如下:
1) 各网点间都有直接相连的路径;
2) 各网点都可以作为转运中心使用;
3) 运输和中转过程中将快递质量作为衡量指标;
4) 网络中可以使用的卡车数量无上限,卡车容量相同;
5) 网点间快递需求的期限要求至少能被直发路径满足。
1.2 模型建立
1.2.1 模型参数
设可以使用的终端网点集合为N,可选为转运中心的网点集合为H,在本文中H=N,i,j,k∈N,分别代表独立的网点。其他参数如下:
cd为每辆卡车单位距离的运输成本;
ct为单位质量的快递装卸成本;
ch为单位质量的快递分拣成本;
dij为网点i到网点j之间的距离;
wij为网点i到网点j的快递总需求量;
Wij为网点i到网点j的紧急需求量;
P为卡车的载重上限;
M为一个足够大的常数。
1.2.2 决策变量
xij为从网点i发出的快递是否经过中转中心j中转,1 表示中转,0 表示不中转;xii=1 表 示网点i被选为转运中心。
sij为网点i直接发往网点j的快递量。
sijk为网点i经转运中心k中转再发往网点j的快递量。
aik为将快递从网点i运输到转运中心k需要的卡车数量。
bk j为将快递从转运中心k运输到网点j预计需要的卡车数量。
eij为将快递从网点i直接运输到网点j需要的卡车数量。
λij为辅助变量,0 表示网点j一定被选为转运中心,1 表示不一定。
1.2.3 混合整数线性规划模型
目标函数式 (1) 中,总成本由3 部分组成,第1 部分表示转运中心的分拣和存储成本,第2 部分表示装卸成本,第3 部分计算3 种路径上的总运输成本。式 (2) 和 (3) 是经典的单一分配约束,每个节点发出的快递需求都必须且只能分配给一个转运中心。式 (4) 规定每个网点发出的中转快递都按照分配好的轴辐式网络运输。式 (5) 和式 (6) 规定了被选中的转运中心不能与其他网点建立直发路径。约束式 (7) 保证快递都会经过混合式网络发出。式 (8) 和式 (9) 为紧急需求的两种运输方式,前者将紧急需求的起始点作为转运中心,即继承前一天的转运中心选择;后者在起始点与目的点之间建立直发路径。式 (10) 为在起始点到转运中心所需的卡车数量。式 (11) 为转运中心到目的点预计所需要的卡车数量,这部分运输过程有可能会随着次日紧急需求的运输决策而产生变动,因此计入的卡车数量为已发生需求的期望卡车数量。式 (12) 为起止点间直发路径上所需的卡车数量。式 (13) ~ (15) 为各个决策变量的取值范围。
2 改进的遗传-退火算法
传统的轴辐式网络设计问题是NP-hard 问题,在快递公司的终端网点构成下,变量规模达到百万级,求解器无法在合理时间内收敛到最优解,为此,本文提出一种改进的两阶段遗传退火算法(genetic simulated annealing algorithm, GSA),将问题分解为两个相互耦合的子问题:轴辐式网络规划和直发路径设计,分别采用遗传策略和退火策略进行求解。算法框架如图1 所示。
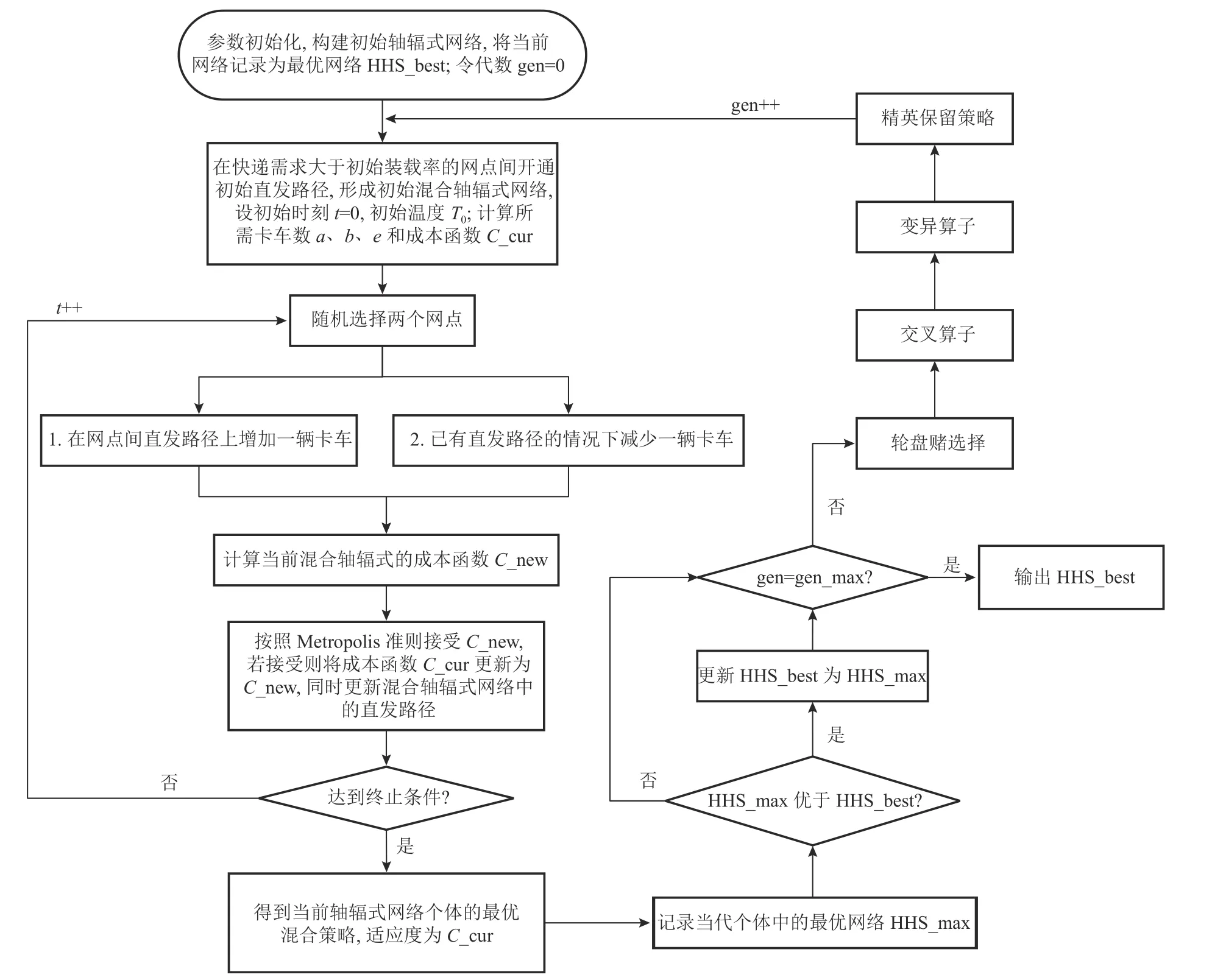
图1 改进的遗传-退火算法的流程图Figure 1 The framework of the improved GSA
2.1 轴辐式网络规划阶段
该阶段在当前的终端网点中选择转运中心,并完成普通网点的转运分配。为了能在全国网点中大范围地搜索转运中心组合,在轴辐式网络规划阶段使用了改进的遗传算法作为主体。
编码方案:每个轴辐式网络被编码为VH和VN两个n维整数向量。VH中每个基因代表一个终端网点,采用0-1 编码方式记录该网点是否被选为转运中心;VN中每个基因的顺序与VH中的一致,分别记录该网点发出的快递被分配的转运中心索引。图2 给出了一个含有7 个终端网点的轴辐式网络规划方案,其中网点2 和网点7 为该运输网络的转运中心。
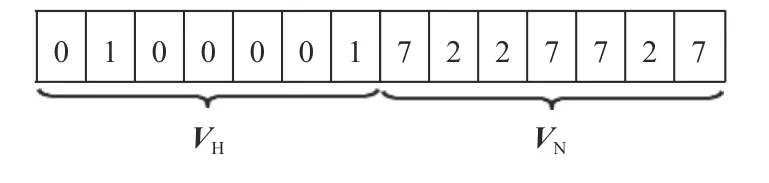
图2 网络规划阶段中一种7 个网点的编码方案Figure 2 A coding scheme of 7 nodes at the network planning stage
初始种群构造:引入一个新的参数g,表示初始种群中转运中心的数量。随机生成g个1~n之间的数字,选择其对应的网点作为转运中心。未被选中的普通网点被贪婪地分配给距离最近的转运中心。
适应度函数:在第2 阶段的直发路径开通完成后计算每个转运中心的装卸、分拣、存储的快递量及3 种路径上的运输量,通过式 (16) 计算适应度值。
Fi表示个体i的适应度值,Ci表示个体i根据式(1) 得到的函数值。Fi与Ci负相关。
选择操作:轮盘赌选择模拟自然选择规律产生可以进行交叉和变异的父代染色体,每个个体被选中的概率pi通过式 (17) 得到。当没有出现优于父代最优个体的子代个体时,通过经营保留策略保留父代最优的个体,并淘汰子代中的最差个体。
交叉算子:在VH段以概率pc使用两点交叉算子进行交叉,对交叉后受到影响的普通网点重新贪婪地分配转运中心。
变异算子:以概率pm随机选择子代个体进行基因突变。可能发生的突变包括从VH中选择一个基因改变其布尔值,或从VN中选择一个基因将其分配给剩余距离最近的转运中心。两种突变发生的可能性相等,突变后同样可能需要对普通网点进行再分配。
2.2 直发路径设计阶段
该阶段在普通网点之间开通直发路径,并计算直发快递量。第1 阶段中的每个个体的适应度计算都需要用到此阶段的优化结果。
完成网络规划后,通过贪婪法构建第2 阶段初始解。在快递需求大于初始装载率r0的网点间开通初始直发路径,形成初始直发路径,初始温度为T0。
在每个温度下进行马尔卡夫链长度的随机扰动,每次随机选择两个普通网点,若两点间尚未开通直发路径,则在两点之前开通直发并安排一辆卡车,否则以相同的概率在网点间的直发路径上增加或减少一辆卡车。时间t时的温度如式 (18)所示。
若扰动后的混合网络总成本低于扰动前,则接受扰动,否则按照式 (19) 中的Metropolis 准则接受扰动后的混合网络。扰动改进将进行至温度低于冻结温度Te或连续q代不接受扰动。
3 算例分析
本文采用某电商在2020 年12 月1 日~5 日的快递需求量数据作为研究算例,其中包括分布在我国东部的30 个城市的终端网点,5 d 中网点间的快递需求量如图3 所示,前2 d 网络中快递需求总量较低,后3 d 总量较高;5 d 中出现需求量峰值的网点快速变动,快递运输需求在空间和货量上的高度离散化特点十分明显。

图3 30 个网点间的快递需求量Figure 3 Express demand between 30 nodes
为了减少现有网络中其他网点对模型有效性检验的干扰,本文将Serper 等[9]提出的传统轴辐式网络构建模型 (optimization model of hub-and-spoke network, Op.H&S) 和变邻域搜索算法 (variable neighborhood search, VNS) 作为对比基准,取5 d 快递需求量的平均值,在30 个终端网点中重构了包括5 个转运中心的传统轴辐式快递运输网络,基于VNS 得到的网络结构如图4 所示。本文提出的混合轴辐式网络模型 (optimization model of hybrid huband-spoke network, Op.HH&S) 使用Cplex 12.9 求最优解,提出的GSA 算法在 Visual Studio 2017 中使用C++实现,所有实验在一台搭载1.8 GHz 的AMD四核处理器和8 GB 内存的计算机上进行。
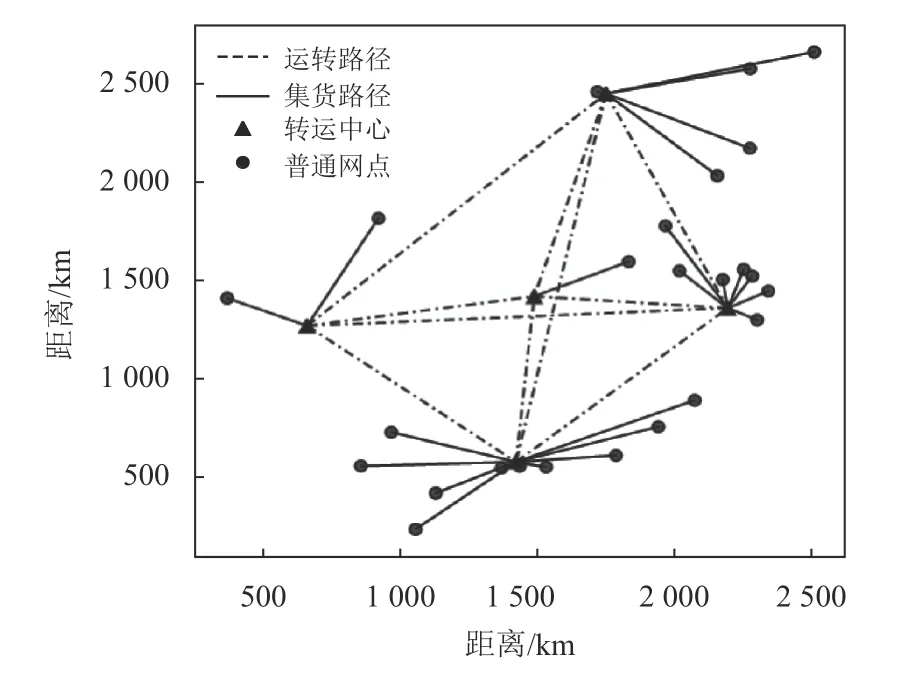
图4 传统轴辐式网络结构Figure 4 A traditional hub-and-spoke network
在实验中,转运中心的装卸成本和分拣存储成本分别为0.02 元/kg、0.03 元/kg,每辆卡车的运输成本为1.5 元/km,载重上限1 000 kg,可以开通直发路径的初始装载率为80%。前一天未完成运输存储在转运中心的快递自动成为后一天的紧急需求。
GSA 算法的遗传阶段中,初始转运中心数量2,与实际运营中的转运中心数量保持一致,交叉概率pc= 0.2,变异概率pm= 0.7,进化1 000 代;退火阶段中,初始温度T0= 1 000 ℃,冻结温度Te=10 ℃,连续终止代数q=20 ,马尔科夫链长度为100。
Op.HH&S 最优解实验在每天的算例上进行3 次,记录最小网络总成本和平均求解时间;GSA算法同样在每天的算例上进行3 次,记录最优结果对应的网络总成本 (total transportation cost, TTC) 和运行时间。基于GSA 算法的第5 d 的混合轴辐式网络结构如图5 所示,为便于观看,省去了转运中心之间的转运路径。
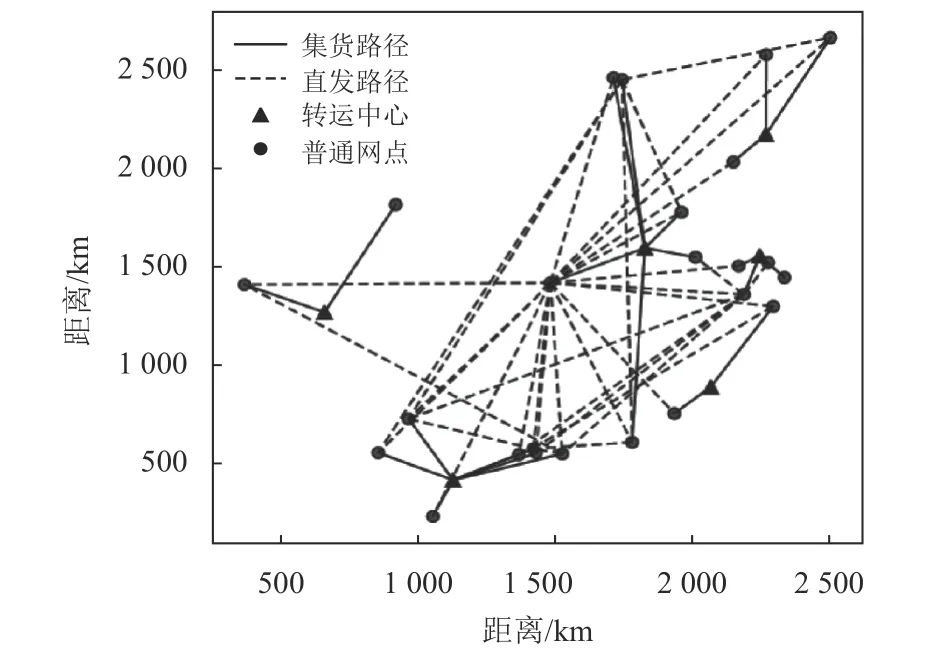
图5 混合轴辐式网络结构Figure 5 A hybrid hub-and-spoke network
Op.HH&S 模型和GSA 算法与传统轴辐式网络模型和算法基准的结果对比如表1 和图6 所示,表中提供了Op.HH&S 相比于Op.H&S 对网络总成本的改进率及GSA 算法距离Op.HH&S 最优解之间的差距。由于传统轴辐式网络计算不需每天进行,在此只记录构建网络时的运行用时。

表1 混合轴辐式网络与传统轴辐式网络的结果对比Table 1 Comparison between HH&S and traditional H&S
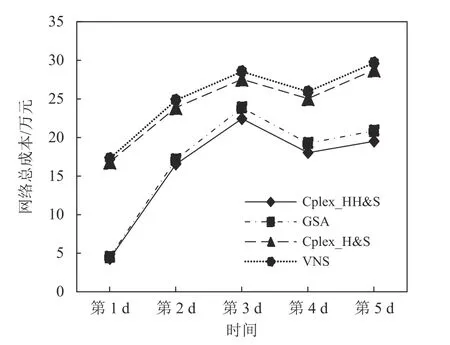
图6 混合轴辐式网络与传统轴辐式网络的结果对比Figure 6 Comparison between HH&S and traditional H&S
对比混合轴辐式网络和传统网络模型的最优解可以发现,基于混合轴辐式网络的再设计方案在5 d中的网络总成本都低于传统网络,其中在无紧急需求需要继承的第1 d,总成本的改进率最高,5 d平均节约网络总成本32.2%,证明了再设计方案对于当前快递公司的实际应用价值。复现的VNS算法与本文提出的GSA 算法分别都能够收敛到与传统轴辐式网络与改进轴辐式网络最优解非常接近的结果,其中GSA 算法的差距可以保持小于5%,5 d 平均差距为3.8%,在实际使用中基本可以代替最优解。两种模型使用求解器进行求解的时间相当,但在保证解质量的前提下,GSA 算法对混合轴辐式网络求解时间的改进更加明显,可以保证每天运输路径计算的效率,不影响快递网点的正常运转。
为了进一步探究各参数值变化对网络总成本的影响关系,分别对单位运输成本cd、单位转运成本ct+ch、卡车载重上限P进行灵敏度分析,以VNS算法和GSA 算法计算得到的结果作为传统轴辐式网络和混合轴辐式网络的网络总成本,5 d 平均网络总成本与各参数变化关系如图7 所示。
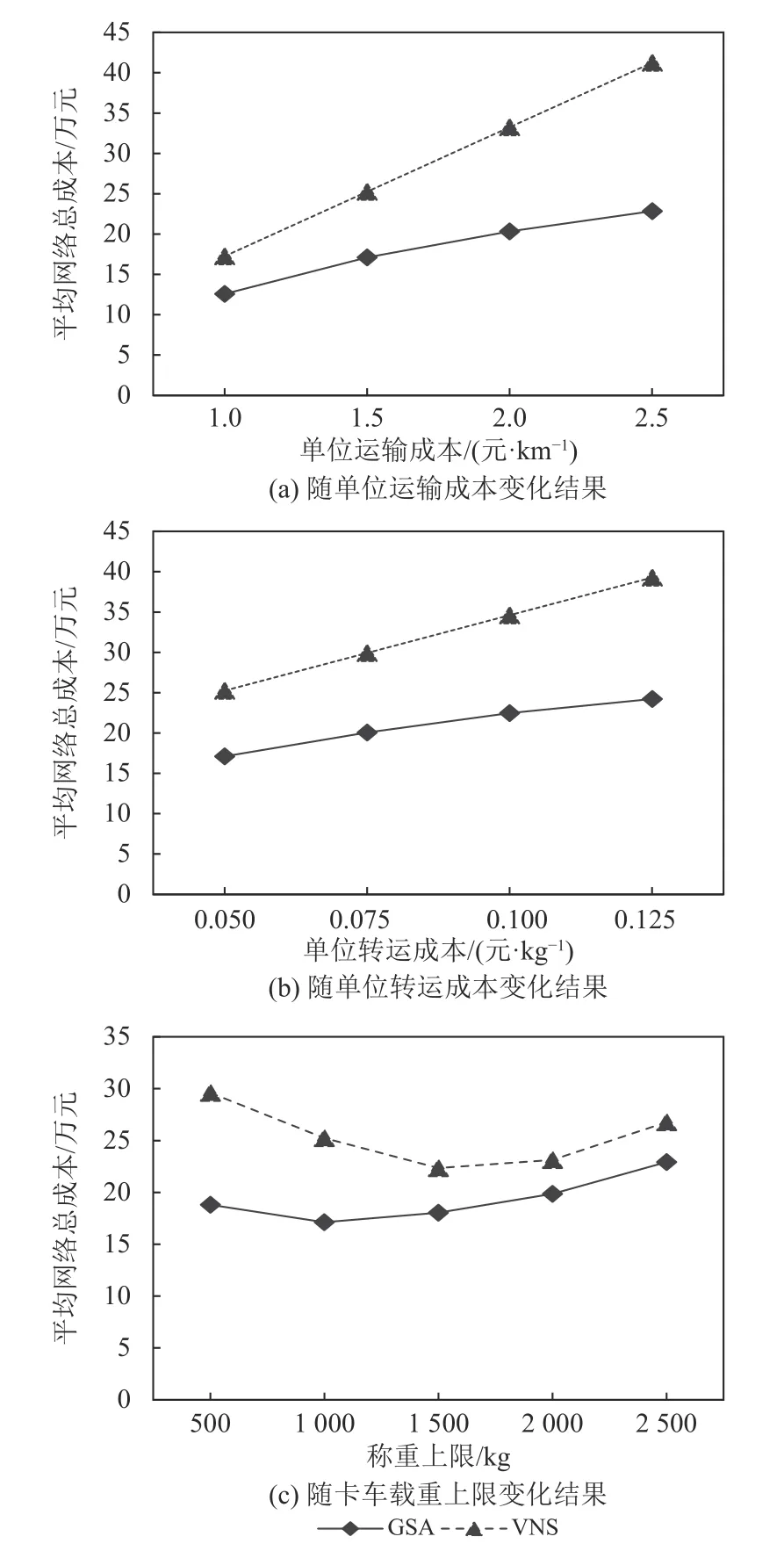
图7 5 d 平均网络总成本的灵敏度分析Figure 7 Sensitivity analysis of the average cost in 5 days
图7 (a) 和7 (b) 分别显示了平均网络总成本随单位运输成本和单位转运成本变化的结果,单位运输成本从1 元/km 增至2.5 元/km,单位转运成本从0.05 元/kg 增至0.125 元/kg,两种成本的增大都会导致两种网络总成本的增加,但混合轴辐式网络再设计方案的成本总是低于传统固定的轴辐式网络,且随着单位运输成本和单位转运成本的增大,两者的差距也不断拉大,再设计方案对单位运输成本和单位转运成本的鲁棒性都优于传统轴辐式快递网络,在未来人力资源等因素带来单位成本提高的情况下,混合轴辐式网络再设计方案可以有效控制网络总成本的增长速度。
图7 (c) 显示了平均网络总成本随卡车载重上限变化的结果,载重上限从500 kg 增至2 500 kg,不同容量的卡车的启动成本也会不同,对总成本的影响较为复杂。实验中随着卡车载重上限的提高,两种网络的平均总成本均呈现先下降再上升的趋势。传统轴辐式网络的拐点出现在载重1 500 kg,说明快递公司可以通过换用更大载重的卡车在一定程度上降低运营成本。但在相同卡车容量下,混合轴辐式网络的平均网络总成本依然总是低于传统轴辐式网络,最优方案即为当前载重1 000 kg 的卡车。因此,快递公司在当前快递需求量下,继续使用载重1 000 kg 的卡车,并每天动态地进行混合轴辐式运输路径规划,可以在最大程度上降低网络总成本。
4 结论
本文针对当前快递运输需求的离散性和波动性特点,提出了基于混合轴辐式网络的运输路径再设计模型,帮助快递公司在当前网点布局下动态地调整每天的快递运输路径,并开发了求解模型的两阶段启发式算法,得到的主要结论如下。
1) 混合轴辐式网络较传统轴辐式网络可以大幅降低快递运输总成本,并在未来对单位运输成本和单位转运成本的变化有更高的鲁棒性。
2) 本文提出的改进遗传-退火算法可以在短时间内得到混合轴辐式网络较好的近似解,可以快速有效地帮助快递公司进行运输路径再设计。
3) 若实验算例中电商快递需求量保持稳定,继续沿用载重1 000kg 的卡车是进行混合轴辐式运输路径再设计的最优选择。
除此之外,本文的研究也尚有一些不足,实际应用中转运中心的动态变化并不单单影响运输成本和转运成本,人力资源等难以量化的因素在优化过程中也需要考虑在内,这将是今后研究的一个方向。
