考虑失效相关性的系统可靠性分配方法

董秋仙，徐闽军，刘汝良，刘 君，夏辰光

(南昌大学 数学与计算机学院，江西 南昌 330031)

系统可靠性分配是将规定的系统可靠性指标自上而下、由整体到局部分配给组成该系统部件，确定系统各组成部件的可靠性要求的过程[1]。其分配的本质是在现有的资源约束条件下实现系统可靠性指标的最大化。

最优可靠性分配方法可构建重要度指标来评比组件对系统的重要程度[2]。在研究部件独立失效的系统上，Wang 等[3]提出一种数控车床的可靠性分配方法；Kim 等[4]提出一种基于子系统故障严重程度及其相对频率来确定可靠性分配权重的方法；Chang[5]整合了有序加权平均树和软集方法，使分配产品的可靠性更加灵活。在研究失效相关性组件的系统上，常使用Copula 函数来考虑组件失效相关的系统可靠性模型。张玉刚等[6]构建了基于Vine Copula 函数的不同失效相关性的串联可靠性分配模型；Navarro 等[7]构建了基于Claytou Copula 函数时刻失效相关系统剩余寿命的可靠性函数。

上述所有方法都改进了传统的可靠性分配方法，但一般无法处理模糊信息。为了解决这一问题，Sriramdas 等[8]将梯形模糊数引入到可靠性分配中；Cheng 等[9]将梯形模糊数与ME-OWA (maximum entropy ordered weighted avarage，最大熵有序加权平均) 算子相结合，提出一种可靠性分配方法。为了更完整地表达可靠性分配过程中的模糊信息，Li 等[10]提出语言中性数加权平均算子 (linguistic neutrosophic numbers weight Muirhead mean，LNNWMM)公式，并首次应用于系统可靠性分配领域中。

随着技术的不断发展，产品正向高精度、复杂性和智能化的方向发展，将会遇到大量的模糊信息产品的可靠性分配。随着影响因素的增加，影响因素之间的相关性对可靠性分配也会产生影响。传统的可靠性分配方法对各种因素的考虑不足，对模糊信息的处理能力较弱，难以得到合理的可靠性分配结果。因此，为了解决传统的可靠性分配方法中对影响因素考虑不足的问题，本文提出子系统复杂度、技术水平、环境条件、成本敏感度、可维修性及运行时间6 种影响因素，前三者采用客观数据定量来描述刻画，后三者通过聚合评价信息使用LNNWMM 算子来评估综合得分。将6 种因素结合获得子系统的分配权重因子，再结合系统可靠性分配模型，通过失效率按分配权重因子比值的方式将系统可靠性指标分配下去，从而分配出各子系统的可靠性指标。

1 系统可靠性分配影响因素

1.1 子系统复杂度 Ii

子系统复杂度定义为子系统所有组成部件数量的相对多少，即

其中，ni表示第i个子系统的部件数量。

考虑到子系统复杂度与载荷分散性有关，谢里阳等[11]提出新的子系统复杂度计算公式“载荷相关复杂度”。

其中，LsRi定义为分散性相对因子。

其中， σsi为施加在第i个子系统上的载荷的标准差；σRi为第i个子系统性能的标准差；LsRi∈[0,1)，当LsRi=0 时，这意味着部件独立失效，不存在失效相关，式 (2) 退化成式 (1)。

但上述子系统复杂度计算公式并未考虑子系统部件之间的结构关系，在不同子系统的部件数量相同的情况下，各部件之间的连接方式不同，子系统的复杂度也会有所区别。例如，一个系统有两个子系统，两个子系统使用相同型号的相等数量的部件，前者所有部件并联，后者所有部件串联，显然并联结构的子系统复杂度会高于串联结构的子系统复杂度。于是，考虑子系统部件之间的结构关系，假设ai为第i个子系统最小路的个数，bi j(j=1,2,···,ai)为第i个子系统第j个最小路的阶数，记用f(ai,bi)表示子系统的结构复杂程度。本文在考虑失效相关系统中提出新的子系统复杂度。

由式 (3)LsRi的计算需要知晓子系统的载荷标准差和性能标准差，而这些值在新产品的设计阶段很难获得，限制了该公式的使用。载荷的分散性与产品的运行环境和产品的性能有关，产品运行环境越好，载荷分散性越小；产品的性能分散性和零件制造工艺、材料加工工艺、产品装配工艺有关，可用技术水平来定性描述[12]，因此可用运行环境Ei和技术水平Mi来近似表示LsRi的大小。基于此，张玉刚等[6]提出新的分散性相对因子公式为

为了使LsRi值更慢收敛到1，本文提出新的分散性相对因子公式为

通过3 种方法计算得到的LsRi值如图1所示，以比值或比值为横坐标，LsRi为纵坐标的变化情况可知，本文得出的载荷相关复杂度LsRi值相对于其他两种方法更慢收敛到1，从而扩大了有效区间。

图1 L sRi 随载荷分散性与子系统性能分散性相对比值变化Figure 1 The variation of L sRi with the relative ratio of load dispersion to subsystem performance dispersion

例如一个由4 个相同结构子系统组成的系统，各子系统分别有4、8、12 和16 个组成单元。当或=3 时，3 种方法计算结果对比如表1 所示，使用载荷相关复杂度得出的4 个子系统Ii基本相同，难以区分。文献[6]提出的复杂度计算方法也有趋于平均的趋势，而本文提出的复杂度方法要比文献[6]提出的复杂度计算方法区分更大。

表1 3 种计算结果对比Table 1 Comparison of the three calculation results

子系统复杂度计算公式为

1.2 结构复杂度 f (ai,bi)函数

如图2 所示为6 种不同结构的子系统，为简化计算，假设各个子系统的运行时间和技术水平一致，所有部件型号相同，部件可靠度R=0.9，分析结果如表2 所示。

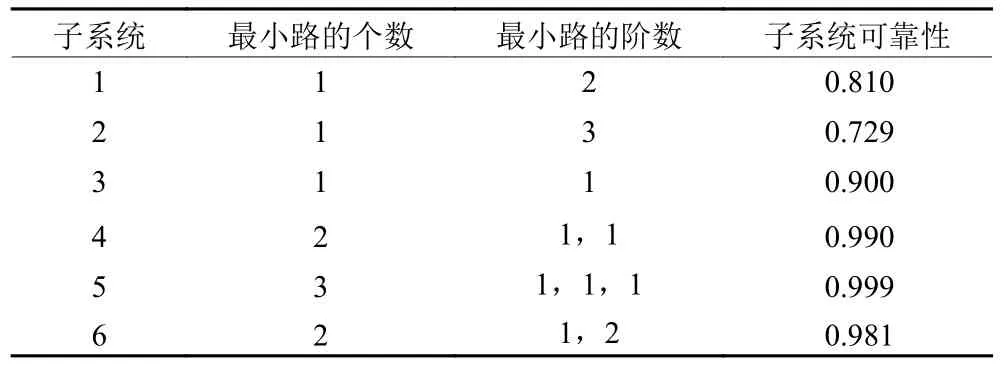
表2 各子系统结果分析Table 2 Analysis of results for each subsystem

图2 6 种不同结构的子系统示意图Figure 2 Six subsystems with different structures

分析和对比第1、4 子系统可知，两者部件数量相等，第4 子系统的最小路个数比第1 子系统多，线路更复杂，可靠性更高。故推断，随着子系统最小路个数ai的增大，子系统结构渐变复杂，f(ai,bi)值增大，可靠度增大。

对比第4、6 子系统最小路的个数和相应最小路阶数可知，两者个数相同，而第6 子系统最小路的最小阶数总体上更大，可靠度更小。故推断，随着bi越 大，结 构 更复杂，f(ai,bi)越大，且子系 统 可靠度会变小。

第1 ~ 6 个子系统的可靠性分别为Ra、Rb、Rc、Rd、Re及Rf。

分析和对比第1、2、6 子系统可知，第2 子系统可视为在第1 子系统上增加1 个最小路的阶数，第6 子系统可视为在第1 子系统上增加一条最小路。观察对比3 个子系统的可靠性，以第1 子系统为参考物，发现增加一条最小路与增加一个数量的阶数作对比，|Rb-Ra|＜|Rf-Ra|。故推断，在其他条件不变的情况下，ai、bij对子系统的影响程度不一样，且最小路的个数对系统的影响程度更高。

分析对比第3、5、6 子系统可知，第5 子系统可视为在第3 子系统上增加两个并联部件的并联，第6 子系统可视为在第3 子系统上增加两个串联部件的并联。观察对比3 个子系统的可靠性，以第3 子系统可靠性为参考物，发现 |Re-Rc|＞|Rf-Rc|。这说明第5 子系统的结构变化量大于第6 子系统，即第5 子系统的最小路个数、最小路阶数的总体影响会超过第6 子系统。

基于上述发现，同时为使子系统结构复杂程度有所区分，使用对数函数刻画各最小路的阶数对子系统结构的影响是个不错的选择，其中，c为常数。故本文构造如下函数。

1.3 技术水平评分 Mi

技术水平代表着产品加工制造采用的技术先进性水平， 技术成熟度是用于衡量技术成熟程度的尺度。中国总装备部内的组织和机构均研究制定了技术成熟度评价标准规范。故可通过确定技术成熟度评分[13]的方法来衡量技术水平，即

其 中，i代 表 第i个 部 件；代表第i部件的技术水平评分；Ai(Ai=0,1,2,···,9)代表第i部件的技术 成 熟 度 等级；Qi代 表 第i部 件 的 等 级 满足 度，Qi∈[0,1]。

设第i个部件的技术成熟度等级为Ai，该等级对应的等级条件共有mi个，邀请n位专家对各项条件的满 足度 进行 评 分。记Ci,u,v为 第v位 专家 对 第i个 部件的第u项条件满足度评分，Ci,u,v∈(0,1]， 则第i个部件的等级满足度为

其中，wi,u为条件权重，且为专家权重，且

由式 (10) 可知，Qi∈[0,1]， 当Qi=0时，说明第i个部件完全没达到等级N的条件要求；当Qi=1时，说明第i个单元完全满足在等级N上的各项条件。

1) 专家权重的计算。

专家权重根据专家与专家组意见的一致程度赋值。某位专家与专家组意见越一致，其给出的评分越重要，其专家权重越高。

设di,u,v为第v位专家对第i个部件的第u项条件给出的条件满足度与的偏差，即

由式 (12) 可知，di,u,v∈[0,1)，且取值越小，说明第v位专家对第v个部件的第u项条件的满足度评分与专家组的平均评分偏差越小。此时，该专家评分的专家权重应更高，故取

其中，pi,u,v∈[0,1)。

2) 条件权重的计算。

由专家权重可知，第i个部件的第u项条件的加权条件满足度评分为

考虑到技术水平评分越低的部件，提高到较高可靠性水平所花费的成本越高，为了避免低估提升部件可靠性水平所花费的成本，故依据加权条件满足度评分越小，其条件权重就越高的这一原则来确定条件权重。

设wi,u为第i个部件的第u项条件的条件权重，则

由分散性相对因子LsRi的定义和取值范围可知，随着运行环境和技术水平的变化，LsRi应取遍 [0,1)，故应对技术水平和运行环境先作无量纲化，再代入公式计算，即

其中，Mi∈[0,1]。

1.4 环境条件 Ei

环境条件代表着子系统运行时所处的环境恶劣程度，取值范围Ei∈(0,1]，所处环境越恶劣，分值越大。

先 考 虑 单 个 环 境 应 力 (如 温 度) 对 部 件i的 影响，设该部件最理想的工作环境条件值为e1，最恶劣的工作环境值为e2，而目前所处的工作环境值为e，则此时的环境条件为

同理，若同时考虑s个环境应力对部件i的影响，分别设该部件最理想的工作环境条件为z1,z2,···,zs， 最恶劣的工作环境值分别为,···,，而目前所处的工作环境值分别为Z1,Z2,···,ZS，则此时的环境条件

其中，wi为各个环境应力的权重。分别统计子系统在一年时间内各环境应力下工作的时间长为ki，则

1.5 子 系 统 可 维 修 性 yi 、成 本 敏 感 性 C oi、运 行 时间 Ti的综合得分

可维护性是指子系统的维护成本和维护时间。更高的可维护性意味着更低的维护成本和更少的维护时间。因此，对可维护性较差的子系统应具有较高的可靠性，以降低维护成本。

在机械加工中心的可靠性分配中，需要在保证机械加工中心可靠性的前提下，尽可能地降低成本。因此在可靠性分配时应考虑成本敏感性 (成本增加/可靠度增加)。较低的成本敏感度对应于提高子系统可靠度的较低成本，因此，一个更高成本敏感性的子系统应该分配更低的可靠度。

在加工中心工作中，并非所有子系统同时工作。不同的子系统有不同的工作时间。当子系统长时间工作时，故障的概率增加，可靠性降低。因此，当子系统长时间运行时，可靠性应该较低分配。

其中LNNs 的相关解释如下。假设有一组语言变量ti(i=0,1,2,···,2h) ， 对于所有的i,j=0,1,· ··,2h，满足以下条件：1) 当i＜j，则ti＜tj；2) 当i=j，则ti=tj；3) 当i＞j， 则ti＞tj。语言变量的操作规则遵守：ti⊕tj=ti+j，r*ti=tri，r≥0。当一个语言的集合存在时，一个离散的集合单位术语集表示为T*={ti|i=0,1，···，2h},h＞0，一个连续的语言术语集表示为T={ti|i∈[0,2h]}，h＞0。

一 个LNN 被 表 示 为 一 个l=(ttrl,thel,tfal)，其 中,ttrl、thel、tfal是3 个独立的语言术语，它们分别代表真实、犹豫和错误的隶属度。

如果 T ERM={ti|i∈[0,2h]} (h>0) 是一个连续的语言术语集，而l=(ttrl,thel,tfal) 是一个LNN，那么l的分 数 函 数 是U(l)=，精 度 函 数 为

综上所述，专家通过使用LNN 分别对Mi、Coi、Ti进行模糊数评价，再通过算子对专家的评价结果进行汇总，最后通过综合分数函数得到其综合得分。

1.6 分配权重的计算

分配权重计算最终考虑的影响因素为复杂度、技术水平，环境条件、成本、运行时间、可维修性。假设 子系 统i的 复杂 度为Ii，成 本、运 行时 间、可维修性的分数函数为Ui，则分配权重计算公式为

获取各个子系统的分配权重后，可通过系统可靠性分配模型计算分配值。分配值可采用失效率按分配权重计算或失效概率按分配权重计算。

2 系统可靠性分配模型

对系统进行可靠性分配需要建立系统和组成部件的可靠性模型，传统的部件串并联的方式在计算系统可靠性时是假设部件之间失效独立进行的，但此方法在应用到组成部件失效相关的产品时则不适用，针对部件失效相关的系统可靠性分配问题常用的是使用Copula 函数。

对于串联系统，可靠性计算公式为

其中，∆表示差分符号，即 ∆xx21f(x)=f(x2)-f(x1)；Cθ为Copula 函数；ui表示随机变量Xi的累积概率分布，在本文中，ui=Fi(t)=1-Ri(t)。

对于并联系统，可靠性计算公式为

为解决系统可靠性分配问题，Copula 函数的种类很多，常见的种类有Vine Copula 函数、Claytou Copula 函数、Gumbel Copula 函数等。本文采用的是Gumbel Copula 函数，其具体表达形式为

其中，θ表示相关程度参数，θ ∈[1,+∞)， θ=1时，代表组成部件之间独立失效。

考虑部件串联连接的失效相关性的系统，要求在T时系统可靠性达到Rs，假设部件的寿命分布服从指数分布，该系统宜使用失效率按分配权重计算，记第i个子系统的失效率为λi，i=1,2,···,n。则

通过联立上述方程组，即可求出在T时刻，系统满足Rs， 各个子系统该分配的可靠性为Ri(T)。

3 应用案例分析

本文以文献[14]的THP6513 重型数控卧式铣镗床主轴系统为例进行分析，系统要求运行500 h时，可靠度-Rs达到0.95。系统可靠度分配考虑的基本影响因素有复杂度Ii、技术水平Mi、环境条件Ei、可维修性Yi、成本敏感性 C oi、运行时间Ti，其中复杂度与组件的数量和子系统的结构有关，使用式(8) 计算。技术水平与产品的使用的规模有关，使用式 (16) 计算。环境条件与考虑的环境因素种类有关，使用式 (18) 计算。可维修性、成本敏感性、运行时间通过专家组借助LNNWMM 算子进行评价得出综合评分。主轴系统的分析结果如表3 所示，其中常数c取值为2。

表3 CNC 主轴系统分析Table 3 Analysis of a CNC spindle system

由文献[14]得到THP6513 重型数控卧式铣镗床主轴系统2017 ~ 2019 年的维修数据，主轴系统共发生144 次故障，其中自动换刀系统发生50 次故障，冷却系统发生26 次故障，润滑系统发生32 次故障，支撑系统发生12 次故障，驱动系统发生22 次故障，测量系统发生0 次故障。因依靠专家组采用技术成熟度规则对6 个子系统评分难度大，故本文用

近似表示各子系统的技术水平。其中，Di为各子系统3 年的故障次数。

本文将环境因素考虑为温度和湿度，根据文献[15]得机床工作的最佳温度为21 ℃，最佳相对湿度为45%，工作最差温度为40 ℃，最差相对湿度为80%，机床车间六月的平均温度为29 ℃，平均相对湿度为63%，为简便计算，假设每月车间平均温度和湿度尽不相同，则温度、相对湿度权重各为0.5，环境条件为

根据文献[13]，可靠性分配小组由TM1、TM2、TM3、TM4 四位专家组成，其相对权重分别为0.25、0.35、0.25 和0.15，专家使用LNN，对6 个子系 统的可 维 修性Yi、成 本 敏感性 C oi、运 行时间Ti3 个因素进行评分。采用的术语集是T= {ti|i∈[0,10]}，其中，t0=最差，t1= 很差，t2=中等差，t3=稍差，t4=差，t5=中等，t6=好，t7=略好，t8=中等好，t9=很 好，t=最 好；权 值 向 量W=(0.25,0.5,0.25) ，参数向量P=(1,1,1)。评分结果如表4 所示，分配结果如表5 所示。

表4 可维修性、成本敏感性、运行时间评分分析Table 4 Score analysis of repairability, cost sensitivity, and runtime

表5 本文方法分配结果Table 5 Allocation results of the proposed method

6 个子系统的分配权重确定后，采用式 (25) 、 (26) 、(27) 可 得： λ1:λ2:···:λ6=1:0.584 5:0.607 9:0.790 3:0.641 8:0.717 8，R1=0.972 0，R2=0.983 5，R3=0.982 9，R4=0.977 8，R5=0.981 9，R6=0.979 8。其中，相关系数 θ取值为2。若考虑子系统独立失效的分配情况，则R1=0.9883，R2=0.9931，R3=0.9928，R4=0.9907，R5=0.9924 ，R6=0.9816。

对比二者的分配结果可知，在系统要求运行500 h 时，可靠度Rs达到0.95 的条件下，通过本文可靠性分配方法得出的6 个子系统的可靠性要求均略低于不考虑子系统失效相关性的可靠性要求，即不考虑部件失效相关性的可靠性分配结果过于保守，在满足所有部件可靠性从而满足系统可靠性指标的情况下，本方法将降低产品的研发和维修成本。镗铣数控机床主轴是一个集机械、电力、液体等于一体的复杂系统，其中一个部件失效常常会引起其他部件正常工作，这说明在研究系统可靠性分配法时考虑部件失效因素是有必要的。

4 结论

本文将影响系统可靠性分配的因素分为复杂度、技术水平、环境条件、可维修性、成本敏感度及运行时间，因子系统复杂度跟本身结构、部件数量和载荷分散性相对因子有关。通过使用子系统的最小路的个数和各最小路的阶数来刻画结构的复杂程度，通过将环境条件Ei和技术水平Mi进行无量纲化后重新定义载荷分散性因子LsRi，从而改进出更为合理的子系统复杂度结果。通过专家组使用LNNWMM 算子描述可维修性、成本敏感性、运行时间的综合得分，再将6 种因素信息融合成新的分配权重因子。针对失效相关的部件串联系统，运用Gumbel Copula 函数建立系统分配模型。最后以某数控机床的主轴系统为例，分配结果与不考虑失效相关性的情况对比，可以在满足系统可靠性指标的条件下降低产品的制造和维修成本，为可靠性分配理论提出一种新的思路方法。