基于三维点云的曲轴同轴度误差测量方法研究*
2024-01-16窦亚萍杨治飞任慧茹顾旭辉隋文涛
窦亚萍 郑 述 杨治飞 任慧茹 顾旭辉 隋文涛
(①山东理工大学机械工程学院,山东 淄博 255000;②淄博市特种设备检验研究院,山东 淄博 255025)
曲轴作为柴油机和发动机的重要组成部件,是主要的动力来源,可以将活塞、连杆的直线运动输出为转矩,进而实现动力的传输[1]。作为动力机械关键零件中最难以保证加工质量的部分,其连杆轴颈、主轴颈等关键位置的圆度、同轴度和平行度与其他形位和尺寸误差对发动机的寿命、噪声和振动等方面有直接影响[2],因而对曲轴轴颈形状误差的检测显得尤为重要。
针对轴颈同轴度的非接触精确测量,国内外学者、企业提出一系列支撑理论。Wang L 等[3]提出一种在同轴度测量杆上以单个激光位移传感器(LDS)对小直径串联孔进行快速同轴度测量的方法,不需要事先测定测量杆的旋转角度,在随机旋转一定次数后根据LDS 的测量值直接计算串联孔的同轴度。他们还提出了同轴度测量杆的数学模型,可通过改变LDS 的安装位置进而实现不同尺寸和数量的串联孔的同轴度测量。Optoquick 是意大利MARPROSS公司最新的曲轴光学测量方案,应用智能图像处理可以实现同步检测工件不同参数,可容纳长度达1 200 mm 和直径达200 mm 的工件,长度不确定度最大为10 μm[4]。宋志化等[5]在同轴度测量问题上搭建了应用波分复用器的激光测量装置,通过波分复用器把发射的信标光和接收的信号光相结合,构成一个可以同时进行发射和接收信号光的模块,与平行光管共同构成同轴度检测系统。该装置测试简单可行,易于搭建。
本文提出一种基于激光扫描仪获取单拐曲轴三维点云的同轴度误差的非接触测量方法,采集得到三维点云数据后,计算获取轴颈最优切片,以Pratt-RLTS 法得到各个点云切片的圆心,可在1 min 内完成同轴度的测量,为生产企业的同轴度快速准确检测提供了一个可行方案,同时可以为未来出现更高精度的激光扫描仪后的同轴度测量方案提供参考。本文主要的研究对象为单拐曲轴,如图1 所示,主要针对的检测两端轴颈分别为D1、D2。
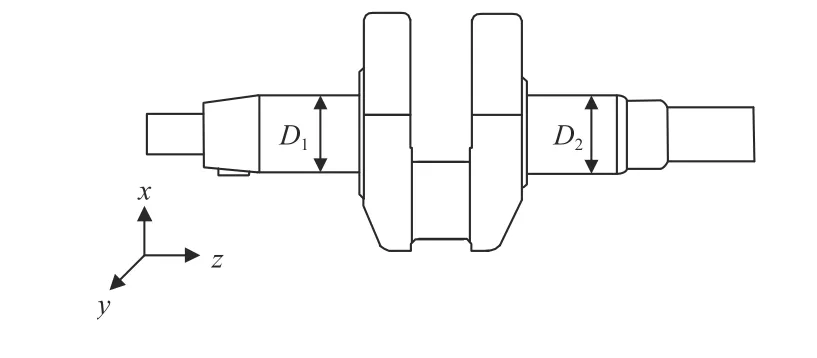
图1 单拐曲轴示意图
1 点云切片的获取
在获取单拐曲轴两端轴颈的点云切片前,需要对采集到的点云数据做去噪、降采样等预处理[6-7],以去除无关背景和噪声点对后续处理结果的影响,同时实现大数据点云的降采样以提高运算效率。背景区域利用平面拟合获取区域点云,并将其去除。对于无效噪点,本文计算了点云与曲轴模型之间的绝对距离,结合条件滤波完成点云去噪。
在本文的同轴度计算中需要获取两端轴颈的多个截面,即在点云数据中,寻找两组等间距切片点云。如图2a 所示,在D1、D2处合适位置处选定一个点沿垂直于z轴方向切割,之后每间隔4 mm 截取一个点云切片。然而在获取点云过程中,由于实验条件受限,采集到的曲轴点云主轴线会与世界坐标系存在一定偏差。如图2b 所示,曲轴点云数据的坐标系o"x"y"z"与世界坐标系oxyz之间存在一定角度偏差,当在点o处沿x轴进行切割时,所得点云切片Cn与理想点云切片Ci相比绕当前圆柱面斜切了一条椭圆形点云带,这会使得后续圆心拟合结果产生很大的误差。

图2 点云切片
针对曲轴主轴线偏移问题,本文截取了D1、D2端轴颈点云集,利用主成分分析(PCA)获取轴颈主轴线的方向向量,将其旋转至z轴,并根据自适应切片算法[8]等间距获取点云切片。
2 拟合截面圆心
2.1 经典代数圆拟合
截面圆心点拟合的准确与否,决定了后续轴线拟合的准确性与同轴度计算的可信度。Kåsa 方法是最为常见的圆拟合方法,计算效率快且方法简单。本文的检测对象较为小巧,待测轴颈直径仅有30 mm。此时应用Kåsa 方法易产生较大误差。Pratt 方法是对Kåsa 方法的改进。对于此类较大曲率圆拟合问题,Pratt 方法有明显优势[9]。
Pratt 方法是一种代数拟合圆法,用来描述圆的代数方程为
将式(1)改写为圆的标准方程:
为确保最终结果为圆,即(a,b,c,d)的值与任一标量相乘的值均不会对圆的方程产生影响,假定a为1。在进行圆拟合时,Kåsa 方法通过计算线性目标函数的最小值来找到拟合圆,Pratt 方法为了消除大曲率圆半径的影响,将F0除以4R2,得式(4)。
应用代数圆参数(a,b,c,d)对圆心、半径进行估计,可以将F1改写为
根据约束条件式(3),可以将目标函数描述为
用矩阵表示该拟合算法,将目标函数F1改写为
该式中的约束条件则变为
为方便求解约束最小化问题,本文引入Lagrange 乘子η,将式(7)转换为无约束最小化函数,并以奇异值分解的方式对其进行求解,最终寻找使F最小的η。
2.2 改进的Pratt-RLTS 拟合方法
本文所研究的单拐曲轴两端轴颈存在花键和小型孔洞,这些部件会导致在使用激光扫描仪扫描点云数据时产生不利于圆拟合的噪声点。如图3 所示,图3a 和图4b 已对点云进行统计滤波降噪与降采样工作,但花键、孔洞处仍存在位置相对集中的噪声点,这将使得代数圆拟合所计算出的圆心位置结果出现较大偏差。此时,经典的Pratt 圆拟合方法已无法满足使用需要。
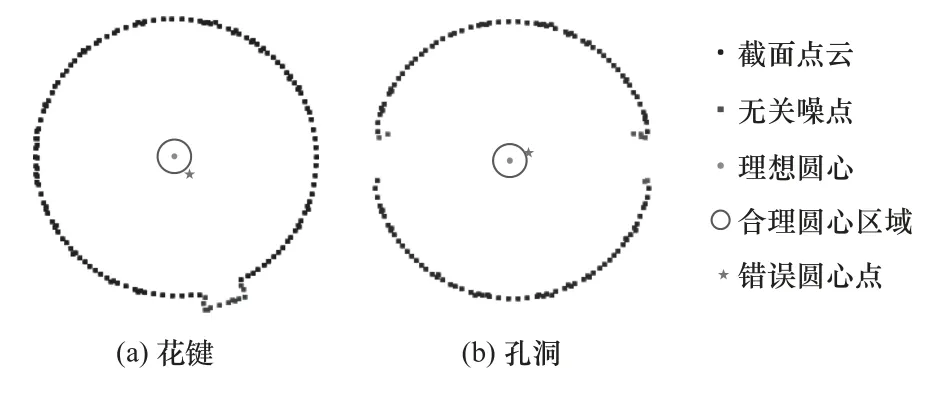
图3 含噪点的轴颈点云

图4 同轴度误差模型
针对以上问题,本文在Pratt 方法的基础上引入最小截平方(LTS)[10]的概念,提出了Pratt_RLTS圆拟合法。首先,根据前文中获取的截面法向量将点云切片旋转至垂直于z轴,把三维圆拟合转换为二维圆拟合,之后以三点定圆的原则,随机选择3个点p0进行初始Pratt 圆拟合,得到初始圆心(x0,y0)和半径R0,计算各点与初始圆之间距离作为残差值ei
利用LTS 中对各点处的残差平方进行排序,通过去除较高的残差平方,最小化p个最小残差平方的和以消除异常值对结果的影响,进而保证结果的稳定性。其优化问题为
式中:m为待估计的参量个数。而对于本文曲轴点云数据,无关噪点占比一般不超过50%,为保证本方法不会达到崩溃点,因此选定p的数值为0.5n。
随机选择p0有一定概率会抽取到无关噪点,进而造成圆心拟合偏差。因此,本文在处理算法中增加了迭代的过程。通过对以上过程进行多次计算,并获取每次迭代结果的残差平方和RSSj:
式中:迭代次数In根据多次测试经验,选定其数值为10。之后对RSSj再次进行排序,进而获取整体残差平方值最小的选点组合,并根据该组合的圆心和半径作为最终的圆拟合结果。
3 同轴度误差评定
对于轴类零件,同轴度表示为轴体中心线与基准轴线之间的重合程度,其公差带根据国家标准规定,是以基准轴线为中心、以公差值为直径的三维圆柱区域[11]。以图4 为例,被测圆柱体D的理想轴线为l,根据D实际表面构建出真实轴线l2,以最小包容区域法寻找其最小包容圆柱区域d。其中,d的中心线与基准轴线l1同轴,Φd即D的同轴度误差,接触点a为l2上距离l1的最大值点,l21与l22为D两端面测定的圆心。
在评价单拐曲轴两端待测轴颈的同轴度时,由于分别作为基准和被测的两个圆柱长度较短且二者之间相距较远,因此会产生一个较大的放大误差[12],如图5 所示。任意截取出两端轴颈长度32 mm 的圆柱,左侧圆柱的第一个截面间隔右侧圆柱第一个截面的距离为115 mm。若此处以左侧圆柱作为基准圆柱,右侧圆柱作为被测圆柱,假设测量轴线在基准圆柱第二截面与基准轴线产生5 μm 的测量误差,根据相似三角形对应边成比例的性质,在测量轴线抵达被测圆柱第一截面时,误差值约为18 μm,而在到达第二截面后便放大至约23 μm,最终测量误差被放大了约4.6 倍。为避免测量放大误差对同轴度误差测量的影响,本文采取两端轴颈的公共轴线作为同轴度的基准轴线,即分别获取两端轴颈多个截面的圆心,根据最小包容圆柱规则获取公共基准轴线,最终以截面圆心至公共基准线的最大距离的两倍作为同轴度的误差值。

图5 大间距同轴度测量放大误差
同轴度基准轴线目前公认最佳的拟合方法为最小包容区域法。然而这种方法的实现难度较大,因此基准轴线一般通过最小二乘法近似表示,或是通过应用优化算法不断迭代逼近。本文此处选择对其采用最小二乘法进行计算。对于空间直线的最小二乘拟合法,需要最小化点云中各点到基准轴线之间的距离平方和。设基准轴线的方向向量为V(u,v,w),且过点P(x0,y0,z0),则空间直线的方程为
式(13)可以改写为
其矩阵形式为
4 实验分析
4.1 圆拟合仿真验证
为验证本文方法对于单拐曲轴轴颈圆拟合的可行性,创建20 组圆心为(0,0)、半径为15 mm 的样本点云圆,每组点云中包含100 个数据点。为尽可能还原真实曲轴轴颈上花键和孔洞处的无关噪点,特设立在任一范围内增加20% 的聚集异常值,如图6 所示。

图6 样本点云
以最小二乘法(LSC)、最小区域法(MZC)、随机抽样一致算法(RANSAC)以及Pratt_RLTS 法对样本点云集进行圆拟合对比验证。由图7 中各方法的结果可知,在圆心横纵坐标的稳定性方面,LSC 与MZC 效果最差,波动较大,且与圆心标准坐标相差较远;RANSAC 与本文所提出的Pratt_RLTS法在多组数据稳定性上较为相近,但本文方法更接近于标准圆心,对于后期单拐曲轴的同轴度误差检测更有帮助。

图7 圆拟合稳定性测试
4.2 同轴度误差测量
本实验研究所采用的激光扫描仪为Faro Design ScanArm,测量范围2.5 m,最小点间距40 μm,同时配备Geomagic®Wrap 软件,以实现单拐曲轴的表面三维扫描点云数据的采集工作。扫描工作过程中曲轴摆放在实验室桌面上,手持激光扫描仪对曲轴点云进行采集,如图8 所示。

图8 点云扫描工作
在实验过程中共获取了10 组曲轴点云,之后按照前文所提到的圆拟合方法依次对点云进行处理。为验证本文同轴度测量的准确性,采用海克斯康公司的三坐标测量机(CMM)INNOVA PERFORMANCE进行对比实验,如图9 所示。该仪器坐标定位精度较高(大于10 μm),分别对曲轴D1、D2端轴颈的多个截面进行了同轴度与圆度测量。应用CMM 进行多次圆度测量后,得到曲轴D1、D2端轴颈的截面圆半径分别为14.978 6 mm 和14.977 4 mm。以D2端轴颈处的普通切片点云Ct1、带有花键噪点的切片点云Ct2以及带有孔洞噪点的切片点云Ct3数据为例,4 种圆拟合方法与CMM 检测结果之间绝对误差值的均值见表1。
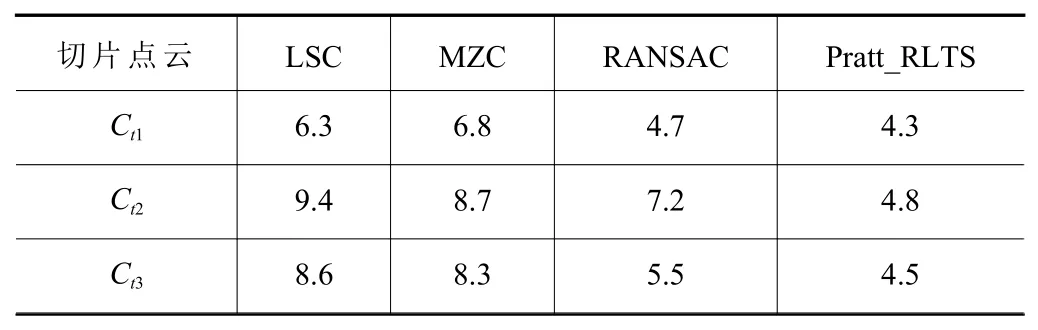
表1 轴颈圆拟合与CMM 检测结果对比μm

图9 三坐标测量机检测同轴度
从表1 中可以看出,4 种对于普通切片点云Ct1的处理结果区别并不明显,其拟合程度的优劣在处理带有花键噪点的切片点云Ct2以及带有孔洞噪点的切片点云Ct3有了明显区别。因为花键以及孔洞噪点的影响,LSC 与MZC 所拟合圆的半径与CMM 检测结果有很大的偏差,最小绝对误差均值仍有8.3 μm;而本文方法Pratt_RLTS 的拟合结果较好,最大绝对误差均值不超过4.8 μm。
对曲轴点云进行同轴度检测,图10 所示为本文方法与CMM 检测的10 组同轴度误差,最大差值仅有5.7 μm,两组数据之间绝对误差的均值为3.9 μm,证明了同轴度误差光学视觉评定方法有较高的准确度,可应用于曲轴同轴度的评定。

图10 同轴度误差值
5 结语
本文为解决曲轴同轴度的快速、准确检测,采用了激光扫描仪的检测方案。在对切片进行圆拟合时提出了Pratt_RLTS 圆拟合法,在Pratt 方法的基础上引入最小截平方的概念,并对最小截平方进行排序以排除噪声点,优化圆拟合结果。通过对存有花键及孔洞噪点的切片点云的实验证明,该拟合方法相较于CMM 检测结果的绝对误差均值不超过4.8 μm,有较高的准确度。后续对曲轴两端轴颈同轴度误差进行检测,与CMM 检测结果相比最大绝对误差仅有5.7 μm,差值平均在3.9 μm,证明了本文检测方案的可行性与准确度。
