内外圈相对倾斜对圆柱滚子轴承寿命的影响＊

魏延刚 段同江 姚金池 吕海霆

（①大连科技学院机械工程学院，辽宁 大连 116052；②瓦房店轴承集团有限责任公司，辽宁 瓦房店 116300）

根据经典弹性接触理论，1996 年燕晓慧等[1]应用数值解法研究了由转子弯曲引起的圆柱滚子轴承内外圈相对倾斜，提出了用滚子修缘和增加轴承径向游隙的方法减小内外圈相对倾斜，从而改善轴承载荷分布。2014 年白晓波等[2]根据弹性接触理论，建立了滚针轴承在内外圈倾斜状况下力学模型，用迭代法对该模型编程求解滚针轴承不同工况下的载荷分布情况，也得出有内外圈倾斜时，适当增加游隙，可改善轴承载荷分布的结论，并指出对滚针修形时应该考虑倾角和载荷对滚针受载影响。

对风电机组齿轮箱圆柱滚子轴承进行优化设计中认识到，滚子类轴承工作过程中由于各种原因引起的轴承内外圈相对倾斜不仅对轴承的载荷分布、接触应力有重要影响，而且对滚子类轴承修形效果和寿命产生直接影响。因此有必要对圆柱滚子轴承在内外圈相对倾斜情况下的接触应力[3]、滚子修形效果和寿命进行深入研究。

20 世纪40 年代瑞典学者Lundberg G 和Palmgren A 提出了滚动轴承寿命计算理论[4]，该理论是在Hertz 接触理论、Weibull 材料强度统计理论和大量实验的基础上建立起来的。国际标准ISO 281:2007[5]基于此制定，并在历次修订过程中融入了润滑、污染、轴承材料的疲劳载荷极限等因素对轴承寿命的影响。

国际标准ISO/TS 16281:2008[6]给出了轴承修正参考额定寿命计算的推荐方法，该方法不仅考虑了ISO 281:2007 中涵盖的各因素，还考虑了轴承套圈偏斜、轴承工作游隙和滚动体内部载荷分布等因素，较适用于风电轴承等特殊应用工况。ISO/TS 16281:2008 的特点在于，更为准确地计算了轴承内部载荷分布情况，特别是对于滚子轴承，引入了切片模型来计算任意滚子的任意切片的弹性变形。

在ISO 281:2007 和ISO/TS 16281:2008 发布之后，虽然有不少关于滚动轴承寿命研究论文见于各种期刊，但大部分是基于ISO 281:2007 寿命计算方法，如牛宝禛等[7]以4.5 MW 风电机组主轴固定端轴承为研究对象，基于ISO 281:2007 标准和Palmgren-Miner 线性损伤累积理论建立疲劳寿命理论计算模型，进行寿命对比计算，对比两计算结果可知，ISO 281:2007 标准修正算法更接近实际工况，并分析了载荷、转速、润滑脂污染程度对固定端轴承疲劳寿命的影响。仅有少数论文是基于ISO/TS 16281:2008 的寿命计算方法，如郭玉飞[8]基于ISO/TS 16281:2008 的寿命计算方法，研究了风电齿轮箱滚子轴承滚动体在不同修形方式下的强度及寿命情况；李桂岩[9]对ISO/TS 16281:2008 和ISO 281:2007 标准中的轴承寿命计算过程中所考虑的因素进行对比，分析出ISO/TS 16281:2008 参考寿命的优势和价值；滕文博等[10]应用Romax Designer 工程分析软件进行了轴承工作温度的单因素仿真试验和正交仿真试验，对比了薄壁深沟球轴承的ISO 281:2007 寿命和ISO/TS 16281:2008 寿命随着轴承温度的变化情况。而关于轴承内外圈相对倾斜对轴承寿命影响的研究论文相对很少。

Romax Designer 工程分析软件滚动轴承的寿命计算方法包括ISO 281:2007 额定动载荷与额定寿命计算方法和ISO/TS 16281:2008 常规载荷条件下轴承修正参考额定寿命计算方法两种标准。常规载荷条件下轴承修正参考额定寿命计算方法的标准ISO/TS 16281:2008 最主要的特点之一是能够计算轴承套圈相对倾斜对轴承寿命的影响，这样应用Romax Designer 工程分析软件便可方便地根据ISO/TS 16281:2008 寿命计算方法研究轴承套圈相对倾斜对轴承寿命的影响。

根据ISO/TS 16281:2008 和ISO 281:2007 计算方法，本文采用Romax Designer 工程分析软件对某大兆瓦风电机组齿轮箱进行整体建模，应用经典滚动轴承理论和“切片法”的基本思想，对齿轮箱输出轴圆柱滚子轴承在内外圈相对倾斜情况下的接触应力、滚子修形效果和寿命进行深入研究；重点介绍轴承在不同内外圈相对倾斜情况下的寿命。

1 内外圈相对倾斜对载荷分布和接触应力的影响

某大兆瓦风电机组齿轮箱高速输出轴轴承为圆柱滚子轴承，其基本代号为NU2332，基本参数为：轴承内径160 mm，轴承外径340 mm，轴承宽度114 mm；滚子数目14，滚子直径40 mm，滚子长度65 mm，轴承内圈滚道直径228 mm。所研究的轴承滚动体和内、外圈的弹性模量、泊松比、热膨胀系数均分别取205 GPa、0.3、12×10-61/℃。

此轴承工作中只承受径向载荷，轴承极限载荷工况下所承受的径向载荷大小为149.1 kN，额定载荷工况下所承受的载荷大小为65.95 kN。本文应用Romax Designer 工程分析软件分析了两个工况，多组内圈相对外圈倾斜量情况下，多组对数修形方案的轴承内部载荷分布、接触应力分布和寿命。考虑到轴承滚子修形应当根据额定工况下所承受的载荷进行，在此，为了节省篇幅，仅给出额定载荷工况下几组典型计算结果来探讨内圈相对外圈倾斜对轴承接触应力、滚子修形效果和寿命的影响。

在对某大兆瓦风电机组齿轮箱滚子类轴承寿命研究中，发现以寿命最长为优化目标所求得的最佳修形量不同于以最大接触应力最小为优化目标所求得的最佳修形量。为了研究内圈相对外圈倾斜对轴承寿命的影响，在相同工况条件下，以寿命最长为最优目标对内圈相对外圈倾斜量γZ分别为0.041 8 mrad、0.176 mrad 和0.535 mrad 滚子进行对数修形优化，得到最佳修形凸度量Lg分别为0.004 4 mm、0.008 8 mm 和0.010 6 mm。

首先，介绍轴承径向载荷为65.95 kN，轴承工作径向游隙为0.027 4 mm，滚子和内、外圈的接触轮廓均为直母线（未修形，Lg=0）和滚子对数修形最佳修形时，内圈相对外圈倾斜量γZ分别为0.041 8 mrad、0.176 mrad 和0.535 mrad 时，轴承内部载荷（滚子与套圈接触力）分布和与最大接触应力分布情况。滚子对数修形凸度量Lg、内圈相对外圈倾斜量 γZ和滚子位置角 ψi如图1 所示。

图1 滚子对数修形凸度量、内外圈相对倾斜量和滚子位置角

由于轴承工作径向游隙为0.027 4 mm 时，无论轴承修形与否，在内圈相对外圈倾斜量γZ分别为0.041 8 mrad、0.176 mrad 和0.535 mrad 的情况下，轴承都只有5 个滚子承受载荷，滚子与内、外圈沿周向的最大接触力和最大接触应力分布图的图形类似，只是承受最大载荷的滚子所承受的最大接触力和最大接触应力数值不同。在此仅给出γZ为0.176 mrad未修形时的滚子与内、外圈沿周向的最大接触应力分布图，如图2 所示。表1 和表2 分别为未修形时和最佳修形凸度量时滚子与套圈滚道间的最大接触力和滚子与内圈滚道间的最大接触应力数据表，Qni是滚子与套圈滚道间的最大接触力，Cpmaxi是滚子与内圈滚道间的最大接触应力（图1）。

表1 未修形不同内圈外圈相对倾斜量轴承内部载荷分布及最大接触应力

表2 最佳修形不同内圈外圈相对倾斜量轴承内部载荷分布及最大接触应力

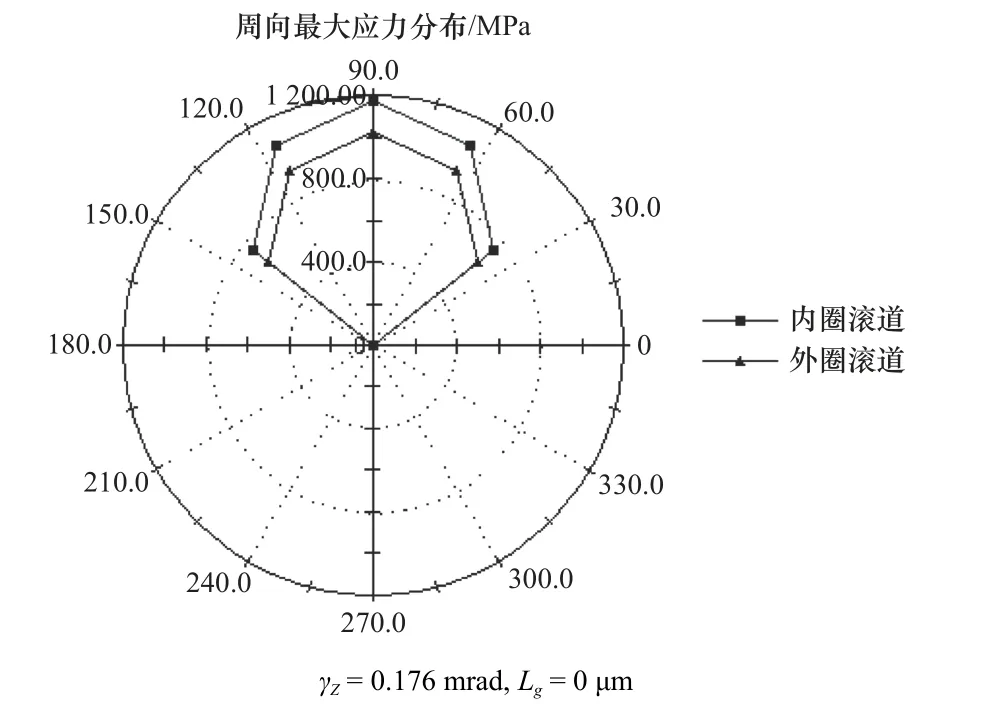
图2 滚子与套圈滚道间沿周向的接触应力分布图

图3 和图4 分别是未修形和最佳修形凸度量时在滚子轴向和滚子位置角构成的平面上表达的内圈滚道接触应力云图，由图3 和图4 可形象地看到滚子修形前后滚子与内圈滚道间的接触应力分布。图5 和图6 分别是未修形和最佳修形凸度量时的滚子与内圈滚道接触应力沿滚子接触母线分布曲线图。注意图5 和图6 中的每条曲线对应相应位置角处滚子的接触应力沿滚子接触母线分布曲线。

图3 滚子与内圈滚道间接触应力云图

图4 滚子与内圈滚道接触应力云图

图5 滚子与内圈滚道接触应力沿滚子接触母线分布曲线图

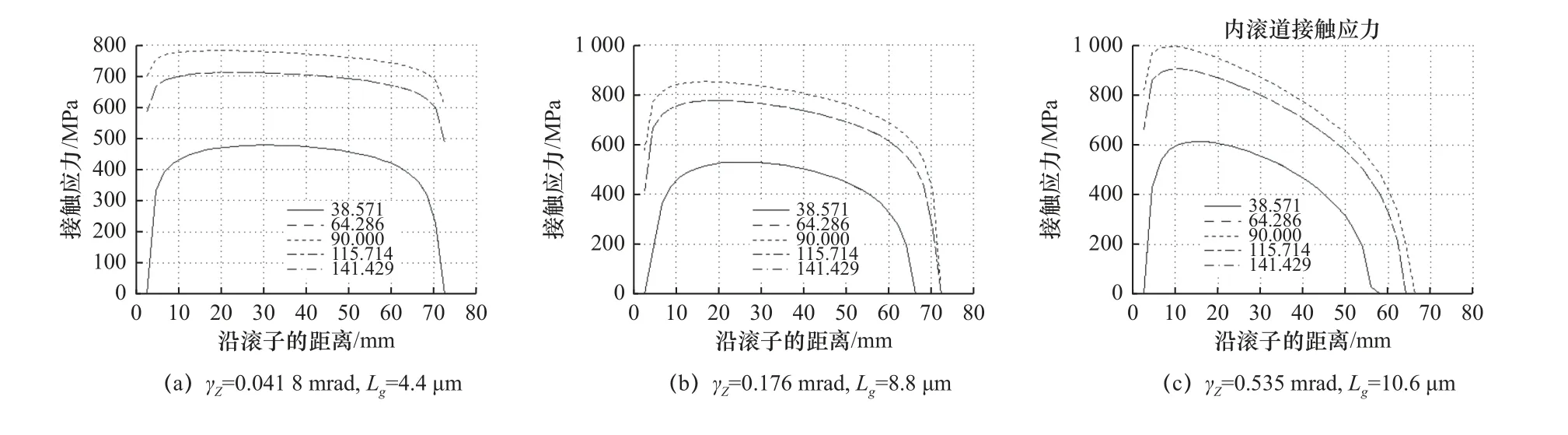
图6 滚子与内圈滚道接触应力沿滚子接触母线分布曲线图

由图3 和图5 可形象地看出，随着内圈相对外圈倾斜量的增大，滚子倾斜幅度和滚子与内圈间最大接触应力增加的幅度越大；接触应力的“边缘效应”，即内圈相对外圈倾斜量越大，滚子倾斜幅度越大，“边缘效应”所产生的最大应力越大。

由图4 和图6 不仅可形象地看出，随着内圈相对外圈倾斜量的增大，滚子倾斜幅度和滚子与内圈间的最大接触应力增加的幅度增大，而且可以看出滚子修形效果。通过对比图5 和图6 可以看出，适当的凸度量完全避免了“边缘效应”，也就是说，虽然内圈相对外圈倾斜量加剧了“边缘效应”，但是适当的修形凸度量完全可以避免“边缘效应”，从而大大降低轴承最大接触应力，提高轴承寿命。

2 内外圈相对倾斜对轴承寿命影响

ISO/TS 16281:2008 给出的计算圆柱滚子轴承修正参考额定寿命的公式[6]：

式（1）中的轴承层k的当量动载荷Pks[9]为

式中各参数的物理意义请参见文献[5]和文献[6]，通过对文献[5]和文献[6]的分析可知，ISO/TS 16281:2008 给出圆柱滚子轴承修正参考额定寿命Lnmr是可靠性寿命修正系数a1的线性函数；是润滑剂污染系数ec和粘度比κ、内圈和外圈轴承层的基本额定动载荷qkce和qkci（或者内圈和外圈的基本额定动态载荷Qci和Qce，注意Qci和Qce分别是由qkce和qkci求和而得）、内圈和外圈的k层切片上的当量动载荷qkei和qkee、轴承层k的当量动载荷Pks、疲劳载荷极限Cur和寿命修正系数aISO非线性的复杂函数。而且a1、κ、eC、qkce和qkci以及Cur和aISO越大，Pks、qkei和qkee越小，则修正参考额定寿命Lnmr越长。

而且轴承内外圈相对倾斜（或者说错位）通过内圈和外圈的k层切片上的当量动载荷qkei和qkee（或者内圈Qei滚道当量动载荷和外圈滚道当量动载荷Qee，注意Qei和Qee分别是由qkei和qkee求和而得）、轴承层k的当量动载荷Pks和寿命修正系数aISO影响修正参考额定寿命Lnmr。

另外，虽然一般的轴承内外圈相对倾斜和滚子修形不会影响到参预承载的滚子数目，但是能够通过影响内圈和外圈的k层切片上的当量动载荷qkei和qkee、轴承层k的当量动载荷Pks，从而影响最大接触力Qni和最大接触应力Cpmaxi。还应当注意到，求解式（1）各参数涉及到的众多参数有的是相互关联的，因此，有些参数对ISO/TS 16281:2008 轴承修正参考额定寿命的影响是复杂的。

表3 是3 个内外圈相对倾斜量时轴承的ISO/TS 16281:2008 额定寿命以及受内外圈相对倾斜量影响的部分参数，注意因为Romax Designer 没有提供qkei和qkee的计算结果，仅提供了Qei和Qee的计算结果，故表3 中给出了Qei和Qee。表3 中第7 行至第9 行给出的是以ISO/TS 16281 寿命最长为优化目标的最优修形凸度量对应的各参数与未修形时对应的各参数的相对差的百分比。

表3 内外圈相对倾斜对与寿命相关参数的影响

由表3 可以看出，轴承未修形的情况下，除了疲劳极限载荷Cur不随内外圈相对倾斜量变化外，其他参数都随内外圈相对倾斜量的变化而变化。内外圈相对倾斜量越大，最大接触力、最大接触应力和内外圈滚道当量动载荷越大，而寿命修正系数越小，从而轴承的ISO/TS 16281:2008 额定寿命Lnmr越短。由表3 可计算出，内圈相对外圈倾斜量 γZ为0.535 mrad 时，ISO/TS 16281:2008 额定寿命Lnmr比0.176 mrad 时的短91.87%，比0.041 8 mrad 时的短97.18%；内圈相对外圈倾斜量 γZ为0.176 mrad 时ISO/TS 16281:2008 额定寿命Lnmr比0.041 8 mrad 时的短65.41%。

轴承修形后，与未修形相比最大接触力有所增加，最大接触应力有较大的降低，内外圈滚道当量动载荷略有降低，寿命修正系数有极大的提高，疲劳极限载荷也有较大的提高。综合结果是ISO/TS 16281:2008 额定寿命Lnmr有极大的提高，内圈相对外圈倾斜量 γZ为0.041 8 mrad、0.176 mrad 和0.535 mrad时，在对应的最佳修形凸度量情况下，ISO/TS 16281:2008 额定寿命Lnmr比未修形时分别提高了111.47%、318.26%和1 054.88%。

值得注意的是，内圈相对外圈倾斜量越大，ISO/TS 16281:2008 额定寿命Lnmr越短，对应的最佳修形凸度量越大，相应修形效果越好，ISO/TS 16281:2008 额定寿命Lnmr提高得越大。

采用疲劳寿命计算系统方法的国际标准ISO 281:2007 的修正额定寿命Lnm由文献[5]可知：

式中：a1为可靠性的寿命修正系数；aISO为基于寿命计算系统方法的寿命修正系数；L10为轴承的基本额定寿命。

径向滚子轴承的基本额定寿命L10由文献[5]可知：

仅承受径向载荷的径向滚子轴承等效径向动态载荷Pr由文献[5]给出：

式中：Fr是轴承所承受的径向载荷。

径向滚子轴承的基本额定径向动态载荷Cr由文献[5]给出：

式中：bm是额定系数，其值随轴承类型和设计而变化；系数fC取决于轴承部件几何形状、各种元件制造精度和材料的因素系数；i是滚动元件的排数；LWe是有效滚子长度；α是公称接触角。

注意国际标准ISO 281:2007 修正额定寿命Lnm的基于寿命计算系统方法的寿命修正系数aISO不同于ISO/TS 16281:2008 修正参考额定寿命Lnmr的寿命修正系数aISO。经过分析可知，ISO 281:2007 修正额定寿命Lnm和与其对应原寿命修正系数aISO都与轴承的内外圈相对倾斜、轴承的径向游隙和修形均无关。

本文所研究的轴承，在相同的工作条件下，内圈相对外圈倾斜量 γZ为0.041 8 mrad、0.176 mrad 和0.535 mrad 时，无论修形与否，计算出的ISO 281:2007 修正额定寿命Lnm均约为5 591 000 hrs。所以，无论轴承是否修形，内圈相对外圈倾斜量不同的情况下，ISO/TS 16281:2008 寿命与ISO 281:2007 寿命相差非常大。在本文的具体条件下，内圈相对外圈倾斜量为0.041 8 mrad、0.716 mrad 和0.535 mrad 时，滚子不修形对应ISO/TS 16281:2008 寿命比相应的ISO 281:2007 寿命相对增加的百分比分别约为563.41%、129.46%和-81.30%；滚子最佳修形量对应ISO/TS 16281:2008 寿命比相应ISO 281:2007 寿命相对增加的百分比分别约为1 302.93%、859.72%和115.92%。

3 结语

通过以上计算结果分析可以得到如下结论：

（1）轴承内外圈相对倾斜通过影响内圈和外圈的k层切片上的当量动载荷qkei和qkee（或者内圈Qei滚道当量动载荷和外圈Qee滚道当量动载荷）、轴承层k的当量动载荷Pks和寿命修正系数aISO，从而影响ISO/TS 16281:2008 修正参考额定寿命Lnmr。内外圈相对倾斜量越大，最大接触力、最大接触应力、内外圈滚道当量动载荷越大，而寿命修正系数越小，从而轴承的ISO/TS 16281:2008 修正参考额定寿命Lnmr越短。

（2）轴承内外圈相对倾斜还影响轴承的修形效果，内圈相对外圈倾斜量越大，不修形的ISO/TS 16281:2008 额定寿命Lnmr越短，对应的最佳修形凸度量越大，相应修形效果越好，ISO/TS 16281:2008额定寿命Lnmr相对提高得越大。因此，不仅计算轴承疲劳寿命时一定要考虑径内外圈相对倾斜的影响，对轴承进行修形优化时也应当考虑内外圈相对倾斜对修形效果的影响。

（3）轴承不同内外圈相对倾斜量情况下，相同修形量效果有所不同，一个内外圈相对倾斜量存在一个相对最佳的修形量。本文所研究的轴承在其他条件相同的情况下，以ISO/TS 16281:2008 额定寿命最长为优化目标内外圈相对倾斜量分别为0.041 8 mrad、0.716 mrad 和0.535 mrad 时的滚子对数修形相应的最佳修形凸度量分别为0.004 4 mm、0.008 8 mm 和0.010 6 mm，相应地ISO/TS 16281:2008 额定寿命Lnmr分别提高了111.47%、318.26%和1 054.88%。

（4）无论轴承是否修形，内圈相对外圈倾斜量不同的情况下，ISO/TS 16281:2008 寿命与ISO 281:2007 寿命相差非常大。在本文的具体条件下，内圈相对外圈倾斜量为0.041 8 mrad、0.716 mrad 和0.535 mrad 时，滚子不修形对应ISO/TS 16281:2008寿命比ISO 281:2007 寿命相对增加的百分比分别约为563.41%、129.46%和-81.30%；滚子最佳修形量对应ISO/TS 16281:2008 寿命比ISO 281:2007 寿命相对增加的百分比分别约为1 302.93%、859.72%和115.92%。

值得注意的是，ISO/TS 16281:2008 给出的轴承修正参考额定寿命计算方法不仅考虑了ISO 281:2007中涵盖的各因素，ISO/TS 16281:2008 的特点还在于考虑了轴承内外圈相对倾斜、轴承工作游隙和滚动体内部载荷分布等因素，更为准确地计算了轴承内部载荷分布情况，特别是对于滚子类轴承，引入了切片模型来计算任意滚子的任意切片的弹性变形，能够计算轴承内外圈相对倾斜、轴承工作游隙和轴承修形对滚子与套圈滚道间应力应变关系的影响，从而能够更加精确地计算轴承的寿命。因此，ISO/TS 16281:2008 计算出的滚子类轴承的寿命比ISO 281:2007 计算出的更接近实际，从而更可靠。

综上，对于滚动轴承，特别是对滚子类轴承进行优化设计时必须考虑轴承内圈相对外圈倾斜对寿命的影响，从而应当采用ISO/TS 16281:2008 推荐的轴承修正参考额定寿命计算方法。