基于拟静力法下复合地层盾构隧道掌子面稳定性分析

姜承军,张道兵,朱欢,源小梦,杨永祥

(湖南科技大学 资源环境与安全工程学院,湖南 湘潭,411201)

自然条件下的地壳板块运动,造成地震频繁发生,从而引起盾构隧道围岩结构破坏[1-2],因此,在地震力作用下,确定盾构隧道的受力情况,计算出合理的支护力,从而保证盾构隧道的稳定具有较重要的价值。

近年来,一些学者对极限分析下隧道的稳定性问题进行了研究。代仲海等[3]以极限分析为基础,构建了复合地层破坏模式,求得了复合地层的最优解,并且分析了地层参数对极限支护力的影响。黄阜等[4]利用极限分析定理,计算出了盾构隧道开挖面上限解。李俊[5]构建了复合地层隧道数值分析模型,在不同支护压力作用下,研究了复合地层隧道开挖面稳定性情况。肖红菊等[6]基于极限平衡理论,计算出开挖面极限支撑压力,并建立了均质土和成层土上覆土压力计算式。王占棋等[7]通过数值模拟手段,分析了在暴雨及地震状态下隧道开挖面的稳定性,并研究了锚杆抗滑桩对隧道的加固效应。汪泓等[8]在运用Baker强度准则的基础上,根据极限分析上限定理,分析了土体强度和地震力对隧道掌子面影响,并研究了各参数对隧道掌子面稳定性的影响。张佳华等[9]将极限分析法与响应面法相结合,建立了多失效模式下盾构隧道掌子面的抗震可靠度模型,求解了地震作用下盾构隧道掌子面的可靠度。SUN等[10]研究了地震作用下隧道开挖对隧道围岩释放应力的力学效应。彭学军等[11]在极限分析的基础上,分析了地层参数以及地震加速度对主动土压力的影响。张佳华等[12]将极限分析上限法和响应面法相结合,构建牛角破坏模式,对软岩隧道掌子面抗震稳定性进行了可靠度分析。

而以上研究都只分析了复合地层下的极限支护力或地震力效应对于单层土体的极限支护力,没有考虑地震力对复合地层围岩所产生的作用,而实际工程中有很多复合地层的情况,因此,本文研究地震效应下复合地层掌子面稳定性,为实际工程提供参考。

1 拟静力法基本理论

拟静力法[13]在隧道的抗震稳定性分析中得到了比较广泛的应用。水平方向的地震力Fh和竖直方向的地震力Fv,表达式依次为

Fh=kh·G

(1)

Fv=kv·G

(2)

式中:kh表示水平地震加速度系数;kv表示竖直地震加速度系数;G表示岩体材料所受重力;为了满足研究不同的地震级数,kh一般为0～0.4,kv=(1/2～2/3)kh。

2 主动坍塌破坏模式

基于已有的研究成果[3],将地震力用拟静力法引入隧道破坏模型中,如图1所示,开挖面前方塌落块体边界线由3条对数螺旋线DC、BC和AB组成,塌落块体ABCD绕极坐标原点O,以角速度为ω作刚体旋转破坏。为简化运算,假定支护力σT在盾构掘进过程中均匀分布,h为盾构隧道的埋深高度,d表示盾构隧道的直径,n表示深度系数,将隧道直径分为nd和(1-n)d两部分,c1、φ1和c2、φ2分别表示上下部分地层抗剪强度参数。

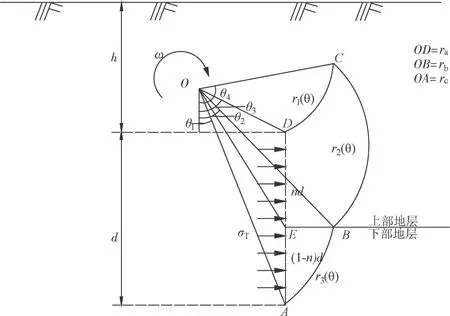
图1 地震效应下盾构隧道掌子面主动坍塌破坏模式Fig.1 Active collapse failure mode of shield tunnel face under earthquake effect

由此可得,对数螺旋线DC、BC和AB的表达式为

(3)

式中:ra、rb、rc分别为OD、OB、OA的长度;θ1、θ2、θ3分别为OA、OB、OD与竖直方向的夹角。

由图1的几何关系可得:

rasinθ3=rcsinθ1

(4)

dsinθ3=rcsin(θ3-θ1)

(5)

rccosθ3-rbcosθ2=(1-n)d

(6)

在对数螺旋线AB上有:

rb=rce(θ1-θ)tanφ2

(7)

将式(7)代入式(6),并简化可得:

(8)

根据式(8)即可求解θ2,此外:

(9)

联立求解式(9)可得:

(10)

3 计算过程

3.1 重力功率

如图1所示,由OBC,OBE区域功率之和减去ODE、OCD区域功率即可求得上部分土体重力功率为

(11)

(12)

(13)

(14)

式中:f1～f2分别为

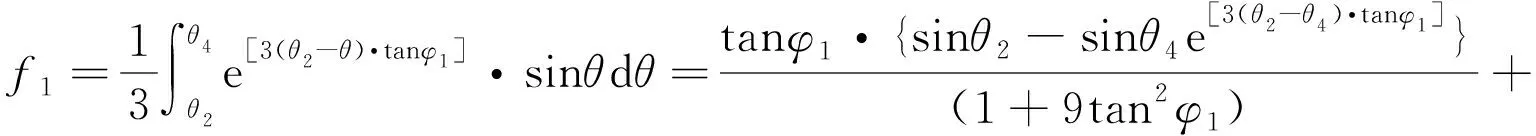
(15)

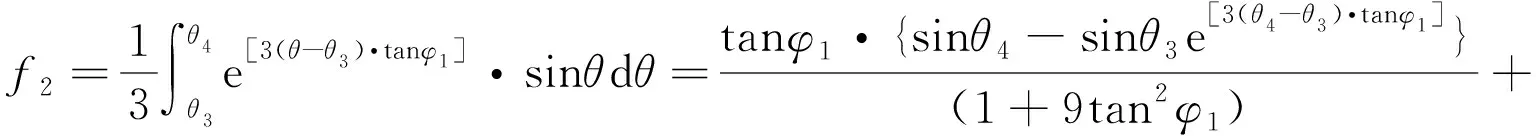
(16)

则上部分土体功率为

Wγ1=Wγ-OBC+Wγ-OBE-Wγ-ODC-Wγ-ODE

(17)

下部分土体重力功率可由OAB区域功率减去OBE、OAE区域功率得

(18)

(19)

(20)

则下部分功率为

Wγ2=Wγ-OAB-Wγ-OBE-Wγ-OAE

(21)

那么,破坏体ABCD土体自重总功率为

Wγ=Wγ1+Wγ2

(22)

3.2 地震力功率

作用在图1的破坏体ABE和BCDE上的地震力功率包括水平地震力功率和竖直地震力功率。

则破坏体ABCD的水平地震功率Peh可由OAB和OBC水平地震功率减去OCD、OAD区域水平地震功率得:

Peh=kh·(Wh-OAB+Wh-OBC-Wh-OCD-Wh-OAD)

(23)

(24)

(25)

(26)

(27)

其中,f4～f6的表达式为

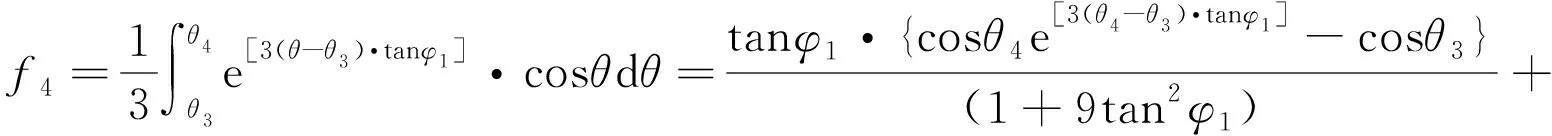
(28)

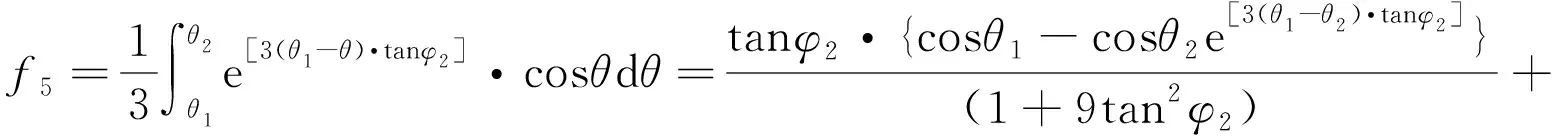
(29)

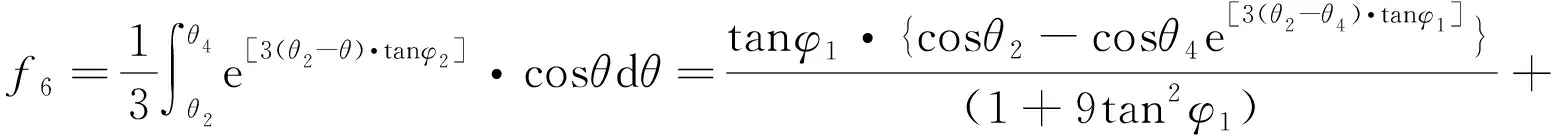
(30)

则破坏体ABE的竖直地震功率Pev1可由OAB竖直地震功率减去OBE、OAE区域竖直地震功率得:

Pev1=kv·(Wγ-OAB-Wγ-OBE-Wγ-OAE)

(31)

破坏体BCDE竖直地震力功率Pev2可由OBC,OBE区域竖直地震功率之和减去ODE、OCD竖直地震功率得到:

Pev2=kv·(Wγ-OBC+Wγ-OBE-Wγ-ODC-Wγ-ODE)

(32)

则地震功率Pe为水平地震功率与竖直地震功率之和为

Pe=Peh+Pev1+Pev2

(33)

3.3 支护力功率

支护力σT在破坏体ABCD上所做的功率为

(34)

3.4 内能耗散率

内部能量耗散发生在间断面CD、AB、BC上,则间断面CD、AB、BC上的能量耗散由CD、AB、BC上的微分面积与黏聚力以及跨间断面的切向间断速度的乘积,即可得到内能耗散率,则CD、AB、BC上的内能耗损率:

(35)

同理,将式(21)代入式(23)中,得出间断面BC内能耗散率为

(36)

同理,得到间断面AB内能耗散率为

(37)

其中,f7～f9的表达式为

(38)

(39)

(40)

总内能耗散率为

WV=WV-AB+WV-BC+WV-CD

(41)

3.5 优化求解

根据外力功率与内能耗散率相等,得到下列方程:

Wγ+Pe-WT=WV

(42)

由式(34)和式(42)可推导出支护力σT的解析表达式:

(43)

(44)

4 验证

代仲海等[3]利用随机极限分析法研究了复合地层盾构开挖面稳定性。将本文计算结果与其数据进行对比,如表1所示。其他参数取值如下:φ1=φ2=30°,γ1=γ2=20 kN/m3,n=0.5,d=10,c1和c2分别为上部地层和下部地层的黏聚力。

表1 极限支护力对比结果Table 1 Comparison resuct of limiting support force

由表1可知,优化得到的结果非常接近文献[3]中的结果,最大误差不超过6%,由此验证了本文方法的可行性。

5 地层参数及地震效应对极限支护力的影响

5.1 内摩擦角的影响

图2为不同深度系数下,极限支护力随内摩擦角的变化图,由图2可知,由于上部土体内摩擦角一定,随着下部地层内摩擦角的增加,极限支护力与下部地层内摩擦角呈负相关趋势逐渐减小,这是由土体自稳能力变强所引起的。而当上部内摩擦角为15°时,深度系数分别为0.3、0.5、0.7,随着下部内摩擦角从10°增加到30°时,极限支护力分别从61.86 kPa减小到8.56 kPa、58.07 kPa减小到9.69 kPa、53.42 kPa减小到11.23 kPa,差值分别为53.30、48.38和42.19 kPa,由此可知,深度系数越小,减小的趋势越明显。当下部地层内摩擦角一定时,上部地层内摩擦角增大,极限支护力反而减小。

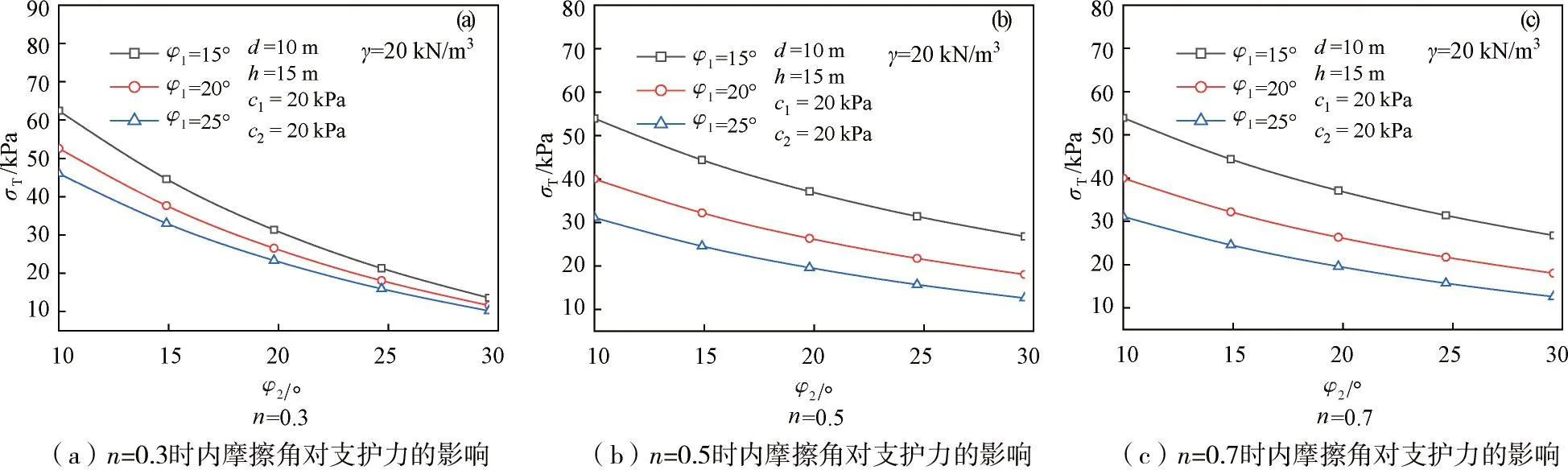
图2 不同深度系数下内摩擦角对极限支护力的影响Fig.2 Influence of internal friction angle on ultimate support pressure under different depth coefficients

5.2 黏聚力的影响

图3为不同深度系数下,极限支护力随黏聚力的变化图,由图3可知,当上部地层黏聚力不变时,随着下部地层黏聚力依次增加,极限支护力与下部地层黏聚力呈负相关趋势在逐渐减小,并且当上部黏聚力为16 kPa时,当深度系数分别为0.3、0.5、0.7,随着下部地层黏聚力从5 kPa增加到25 kPa时,极限支护力分别从48.92 kPa减小到19.59 kPa、46.14 kPa减小到20.85 kPa、42.86 kPa减小到22.32 kPa,差值分别为29.33、25.29和20.54 kPa,由此可知,深度系数越小,减小的趋势越显著。当下部地层黏聚力一定时,上部地层黏聚力越大,极限支护力反而越小。

图3 不同深度系数下黏聚力对极限支护力的影响Fig.3 Influence of cohesion on ultimate supporting pressure under different depth coefficients

5.3 地震效应参数的影响

由图4(a)可知,当竖直加速度一定时,随着水平地震加速度系数kh增大时,极限支护力与kh呈正相关趋势增加。从图4(b)可知,当水平加速度一定时,随着竖直地震加速度系数kv增大,极限支护力与kv也呈现出正相关的趋势增加。因此,地震加速度对隧道支护力有显著的影响,在地震频发的地方,加强抗震设计很有必要。

图4 地震加速度对支护力的影响Fig.4 Influence of seismic acceleration on supporting pressure

6 破裂面图

Z轴是开挖方向,Y轴是垂直方向,由图5(a)可知,伴随着上部地层的内摩擦角取定值时,当下部地层内摩擦角φ2依次增大时,破坏面向隧道面移动,并且破坏的高度降低,破坏面的体积也在减小,即破坏范围随着内摩擦角增大反而减小。由图5(b)可知,当上部地层黏聚力c1取定值时,伴随着下部地层黏聚力c2逐渐增大,破坏面稍向隧道面移动,破坏的高度降低,但变化的范围不明显。从图5(c)可知,水平地震加速度系数kh对复合地层围岩破坏范围影响很小,但随着kh增大,破坏范围也在增大。从图5(d)可知,随着竖直地震加速度系数kv增大,复合地层破坏区域也在扩大。

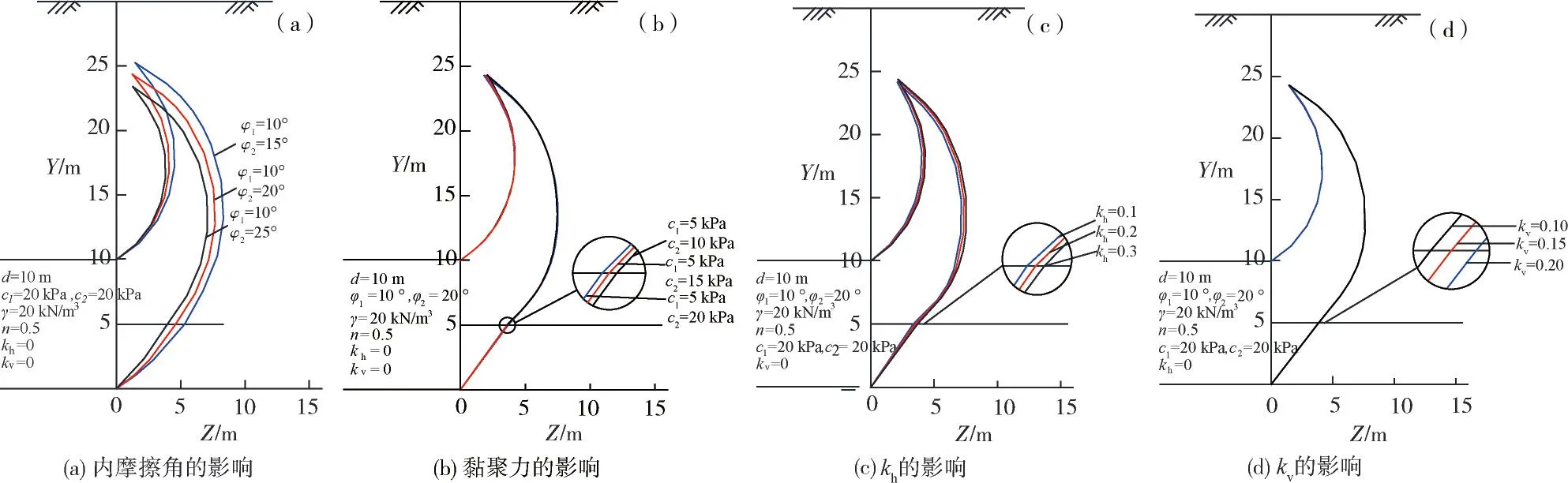
图5 参数对破坏面位置的影响Fig.5 Influence of parameters on the position of failure plane

7 结论

1)极限支护力随着上下地层的内摩擦角增大而减小,且随着深度系数减小,减小程度越明显,并且随着土体下部内摩擦角增大,潜在破坏面位置均向隧道面靠近,破坏范围逐渐减小。

2)极限支护力随着上下地层的黏聚力增大而减小,且随着深度系数减小,减小程度越明显。随着土体下部黏聚力增大,潜在破坏面位置均向隧道面靠近,破坏范围逐渐减小。

3)随着水平或者竖直地震加速度的增大,复合地层极限支护力逐渐增大。随着水平和竖直地震加速度增大,潜在破坏面位置远离隧道面移动,破坏范围逐渐增大,但变化范围不明显。