双线隧道施工对邻近管线安全性的影响

高召宁,燕帅,梁洪瑞

(安徽理工大学 矿业工程学院,安徽 淮南,232001)

目前,我国城市地铁正在快速发展,但城市地下空间复杂,修建着许多重要的基础设施,如地下管道、综合走廊等。地铁隧道施工会造成周围地层的扰动,近距离穿越会给邻近管线产生较大的附加应力,轻则会引起管道沉降,严重会引起管道爆管、管道漏损等事故。因此,在地铁建设中,保护邻近管道的安全尤为重要。

很多学者对地铁隧道施工过程中邻近管道的安全性进行了研究。现有的文献主要集中在管线-土体相互作用关系[1-4]、管线变形的位移计算及力学研究[5-7]等,在管线的安全性判别研究方面,裴子钰等[8]重点研究了隧道开挖下管线受力情况,得到了管线受力变形的主要影响因素;陈志敏等[9]把地表横向沉降与沉降槽宽度系数作为沉降控制参数,制定安全的管线控制基准;赵智涛等[10]考虑到管线的刚度,以地层沉降来代替管线沉降进行判定;周伟等[11]结合管线沉降主要控制指标,根据风险等级来确定管线安全等级,提出管线保护控制措施和应急方案。高丙丽等[12]用地层的监测数据,以地层沉降来反映管线的变形。现有的研究主要是单线隧道施工,缺少理论计算或者计算过于简单,很少能够直接应用于实际工程,并且在实际情况中,城市地铁隧道施工主要以双线隧道为主,双线隧道施工开挖对邻近管线的影响比单线隧道影响会更大,因此,研究双线隧道施工对管线的判别显得尤其重要。

本文以杭州某盾构区间双线隧道工程为研究背景,在现场监测的基础上,用改进的Peck公式对地下管线进行计算,与实测值、数值模拟数值进行对比研究,验证其方法的可靠性,为该类工程提供计算方法和依据。

1 工程实况

杭州某地铁区间隧道总长为3 414.0 m,左线总长为1 760.0 m,右线总长为1 754.0 m。区间平面线形较为简单,线路纵断面呈“V”字形坡,最小平曲线半径为1 500.0 m,最大纵坡为20.825‰,区间隧道顶覆土埋深约为13.2～27.7 m。双线盾构隧道中心相距20 m,埋深为25.4 m,盾构区间有一条混凝土排水管与地铁隧道垂直,管线埋深为4.1 m,管线的外径为0.8 m,管壁厚为0.15 m,管-隧位置及测点如图1所示。

图1 管-隧位置及测点示意图Fig.1 Pipe-tunnel position and measuring point diagram

盾构区间自上而下主要地层为:人工填土、粉质黏土、全风化粉砂岩、强风化粉砂岩、中等风化粉砂岩。盾构机主要穿越地层为中等风化粉砂岩和强风化粉砂岩,土层及材料力学参数如表1所示。

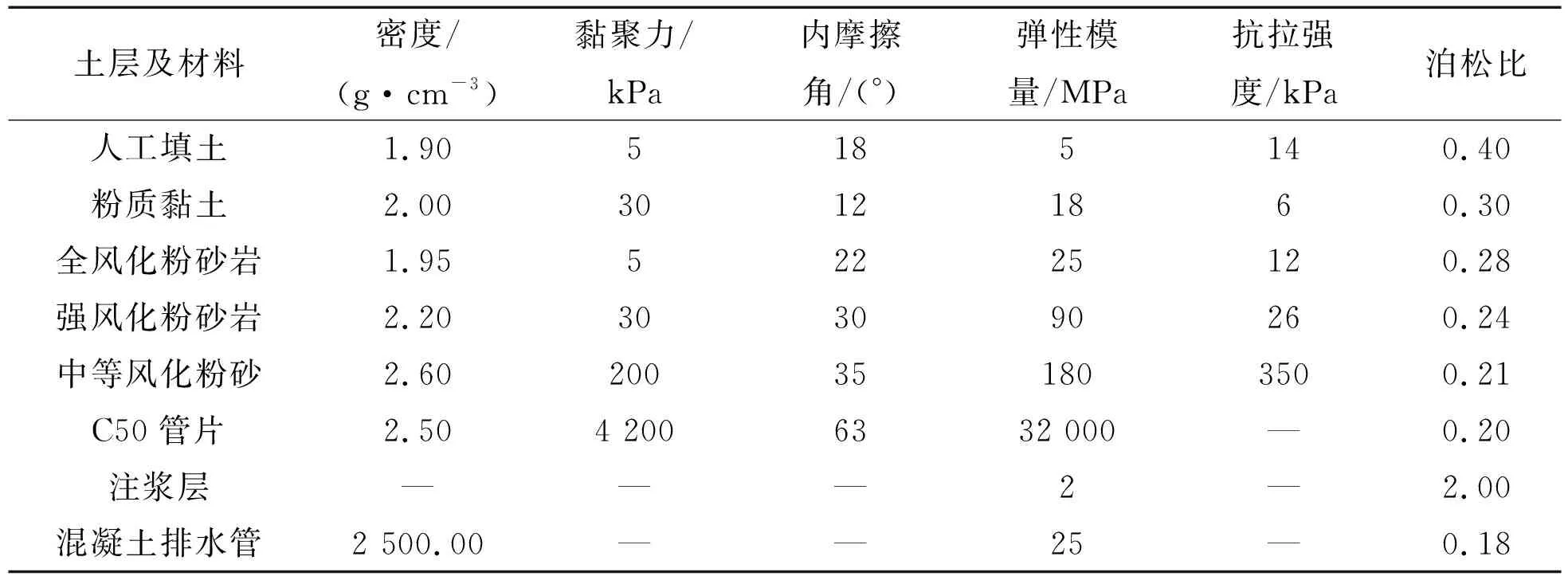
表1 土层及材料力学参数Table 1 Mechanical parameters of soil and material

2 隧道-管道数值计算模型建立

地铁隧道衬砌结构外径为5.4 m,内径为4.5 m,盾构隧道埋深为20.0 m,双线隧道中心点间隔20 m,衬砌为预制钢筋混凝土管片,管片宽度为1.2 m,厚度为0.3 m;管片衬砌后与隧道围岩之间会存在一个环形建筑空隙,需要用注浆材料进行填充,将注浆层厚度设置为0.2 m,弹性模量取2 MPa,为减轻边缘效应的影响,模型长×宽×高为80 m×60 m×50 m,取与管线平行方向为X轴,垂直与管线方向为Z轴,与隧道平行方向为Y轴,建立三维坐标系,计算过程中地面施加0.1 MPa的均布荷载,盾构区间采用的是复合式土压平衡盾构机,模拟时采用空模型进行土体的开挖,向掌子面施加8 000 kN的掘进压力。计算模型如图2所示。管-隧位置关系如图3所示。

图2 管-隧三维数值计算模型Fig.2 Three-dimensional numerical calculation model of pipe-tunnel

图3 管-隧位置关系图Fig.3 Pipe-tunnel position relationship diagram

3 结果分析

3.1 管线沉降过程

在盾构隧道施工的工程中,盾构隧道施工按照盾构隧道掘进阶段主要分为盾构掘进开始阶段、盾构掘进过程和盾构掘进完成3个阶段,管线的变形主要集中在盾构掘进过程阶段,管线的变形主要是地层变形产生的附加作用力引起的。

图4是双线盾构隧道贯通后管线沉降曲线。盾构机在双线隧道的掘进过程中,管线沉降在掘进过程阶段先增加后减下,最大沉降均发生在隧道轴线上方,右线贯通时沉降曲线最大值大于左线隧道贯通时的沉降,沉降槽宽度也明显大于左线隧道,这是因为在右线掘进的过程中,右线隧道会对左线隧道二次扰动,双线隧道相互作用,进而造成位移沉降叠加,管线沉降模拟结果最大值为7.43 mm,实测值为7.25 mm。

图4 管线沉降曲线Fig.4 Pipeline settlement curve

由图4可知,管线沉降的模拟结果与实测结果基本一致,管线沉降曲线近似看呈正态分布,但是实际工程现场同一层土体分布也略有差距,实际工况中管线有管片保护和其他保护措施,这导致实测结果会小于模拟结果,但该模拟已经较为准确模拟管线沉降规律,具有可靠性和准确性。

3.2 管线内力

工程设计中管线是否遭到破坏,主要考虑的是管线的结构应力是否小于材料本身的结构。管线的初始环向应力和纵向应力都较小,一般不考虑。左线隧道贯通管线环向应力、纵向应力如图5所示,右线隧道贯通管线环向应力、纵向应力如图6所示。

图5 左线隧道贯通管线应力分布图(放大10 000倍)Fig.5 Stress distribution map of left line tunnel through pipeline (magnified 10 000 times)

图6 右线隧道贯通管线应力分布图(放大10 000倍)Fig.6 Stress distribution map of right line tunnel through pipeline (magnified 10 000 times)

左线隧道贯通后,管线受隧道开挖的影响,管线的最大压应力出现在左线隧道上方的管底,最大压应力为0.97 MPa,拉应力主要出现在左侧隧道轴线上方两侧,拉应力最大值为0.63 MPa,管线受到“上拉下压”的趋势,管线变形整体呈“V”形分布。右线隧道贯通以后,右线隧道盾构施工会使土体遭到二次扰动,管线内的应力将会重新分布,原有的管线变形向两侧扩展,管线的倾角变大,使得管线变形从“V”形到“W”形过渡,管线的最大压应力为1.11 MPa,最大拉应力为0.65 MPa。

整个隧道施工过程中,管线受到最大压应力大于最大拉应力,最大压应力为1.11 MPa,最大拉应力为0.63 MPa。本工程管线材质为刚性混凝土排水管,根据刚性材质应力判别标准[13],如式(1)所示。刚性混凝土排水管压应力最大允许值为[σ]=15.0 MPa,拉应力最大允许值为[σ]=1.04 MPa。因此,本工程管线处于安全状态。

σmax≤[σ]

(1)

式中:σmax为管线横截面受到的最大压拉应力;[σ]为管线材质容许的压拉应力。

3.3 弹性地基梁理论

此处运用Winkler弹性地基梁理论,假设土体为土弹簧,管线为横架在土弹簧上的地基梁,为了简化模型,此处忽略管线的自重、管线内的液体,具体见图7。管线和土体共同作用可以分为3个阶段,即盾构掘进开始阶段、土-管共同形变阶段、土-管相互分离阶段。1)盾构掘进开始阶段,管线同时受到土体的压力和下部的反作用力而达到平衡。2)土-管共同形变阶段,双线隧道在开挖的过程中,盾构开挖会造成一部分土体损失,打破管线上方和下方作用力的平衡,管线下方土体的作用力小于上方作用力,产生整体向下的附加荷载,此时在土体附加荷载的作用下,管线会发生变形,同时下方弹簧受力也会增加,在此过程中,管线变形先增加后减小,在隧道正上方时管线变形最大。3)土-管相互分离阶段,管线与土层将相互分离。由于本文管线属于刚性管线,管线刚度大于土体刚度,管线沉降时会产生抵抗力,管线会在上部土体与土弹簧之间发生相互作用,进而达到受力平衡。

图7 弹性地基梁示意图Fig.7 Schematic diagram of elastic foundation beam

4 经典Peck公式及修正

4.1 经典的Peck公式

PECK[14]通过隧道周边的地表实测数据,给出隧道直径、土层厚度、地层损失等参数之间的表达式,如式(2)所示。Peck公式认为地表沉降槽近似为正态分布(图8),各地层损失的体积近似等于地表沉降槽的体积。

图8 经典Peck公式沉降槽示意图Fig.8 Classical Peck formula settlement tank diagram

(2)

(3)

VL=V1πR2

(4)

(5)

式(2)～式(5)中:Sx为地表与中心轴距离为x的沉降量;Smax(x)为隧道中线沉降最大值;V1为各地层损失率;i为沉降槽宽度系数;R为隧道外径;z为隧道轴线中心点到地表的土层厚度;λ为土层内摩擦角的加权平均值;VL为双线隧道施工后造成的地层损失量。

4.2 双线盾构隧道施工的Peck公式修正

经典的Peck公式主要研究单个隧道施工引发的地表沉降,但是在实际工况中,盾构隧道施工主要以双线隧道为主,双线隧道对地表的沉降比单线隧道复杂,双线隧道开挖地表沉降槽示意见图9。双线隧道开挖会造成相互扰动影响,本文设定相互扰动影响系数为T,左线隧道施工对右线隧道施工扰动系数为T12,右线隧道施工对左线隧道施工扰动系数为T21。在经典的Peck公式基础上,石杰红等[15]提出了双洞体的Peck修正公式,得到了双线隧道改进的新型Peck公式为

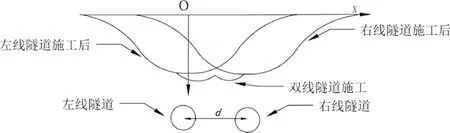
图9 双线隧道开挖地表沉降槽示意图Fig.9 Double line tunnel excavation surface settlement trough schematic diagram

Sx,z=[JB({]S1,z,x∈(-∞,x1]
S2,z,x∈(x1,+∞)[JB)]

(6)

(7)

(8)

Sz=S1,z+S2,z

(9)

式(6)～式(9)中:d为隧道中心点之间的距离;S1,z、S2,z分别为左右线隧道开挖后管线的沉降量;Sz为双线隧道叠加后管线的沉降量;x1为双线隧道中心边界。

4.3 Peck公式计算管线沉降

Peck公式不仅用于计算地表的沉降,还可以计算地表下土体的沉降。管线的变形主要是通过盾构隧道施工引起土体的形变,进而传递到管线的变形。考虑到计算方便,把管线的变形等效其所在土体的变形。相互扰动影响系数T取决于双线隧道净距d,结合图9所示,当净距d较近或者较远时,双线隧道开挖不再进行相互扰动,T12=T21=0,此时改进的Peck公式(8)应变为公式(10),管线变形只受单个隧道的影响,双线隧道盾构隧道施工后,管线沉降曲线趋势基本一致,管线沉降最大值均为隧道中心点的上方。当净距d适中时,双线隧道开挖会进行相互扰动,T12≠T21,此时右线隧道开挖管线沉降应为Peck公式(8),右线隧道施工后,管线变形达到最大。改进的Peck公式分析的结果与数值模拟、实测结果基本趋于一致。

(10)

工程中土层内摩擦角加权平均值为23.4°,隧道所在的土层为强风化粉砂岩,隧道埋深为25.4 m,双线隧道中心距离为20 m,代入式(5),求得i=15.4。由式(4)可知,盾构隧道施工引起的地层损失量与地层损失量及隧道外径有关,隧道外径为5.4 m,由于现有的隧道施工技术已经相对成熟,地层损失率一般控制在0.1%～0.5%,考虑到本工程采用盾构隧道施工以及管线防护和其他防护措施,取地层损失率为0.1%,把数据代入式(4),可得VL=0.092 0,Smax1=Smax2=0.002 4。

工程在双线隧道施工中间隔时间较长,可考虑为T12=T21=0,隧道之间的距离为20 m,管线发生沉降最大量时距离轴线横向距离为30.1 m,把上述i和VL代入式(7)、(8)、(9),求得最大沉降为7.65 mm。

5 结论

1)双线隧道施工中,管线受到的最大压应力、最大拉应力均小于管线最大允许值,管线处于安全状态。

2)通过Winkler弹性地基梁理论,对邻近管线在双隧道盾构施工中的受力情况进行分析,力学分析出的结果与数值模拟的受力情况相吻合。

3)修正Peck公式计算出的最大沉降为7.65 mm,数值模拟出的最大沉降为7.43 mm,实测值为7.25 mm, 修正Peck公式计算出的结果与数值模拟出来的结果与实测值三者基本一致,表明修正Peck公式和模拟结果的准确性和实用性。

4)修正Peck公式计算出沉降结果与数值模拟出的沉降结果和沉降实测值均小于10 mm,根据地下管线的特点,要求沉降控制10 mm以下,由此得出,双线隧道下穿邻近管线安全性风险可以控制,较为安全。