基于CFD的管汇阀门抗气蚀数值模拟研究

2024-01-16尚照辉

河南科技 2023年23期

尚照辉

（1.河南《创新科技》杂志社，河南郑州 450000；2.浙江大学建筑与工程学院，浙江杭州 310058）

0 引言

海底管汇是把采油系统进行集成，形成集中的海底管汇切换控制系统，相当于海底油气采集转运控制中心［1］，是一种高价值深水水下生产系统，其主要系统和部件具有投资成本高，恢复、修理和更换故障设备复杂，费用高等显著特点［2］。油气采集转运控制系统、管汇系统的关键部件为各式各样的阀门，这些阀门分布在管汇系统各个子系统中，并通过控制不同子系统进行分工合作，在整个管汇系统中，阀门起到控制、分流、运输等功能。阀门的结构可靠性和精准性是保证深水石油开采的两大关键因素，因此，有必要对阀门部件进行可靠性分析、结构优化、数值模拟和性能分析，从而有效降低阀门使用风险，并提高阀门使用寿命。

郝露菡等［3］基于FTA 法对某增量式数字阀可靠性进行研究，指出阀门卡停现象会对机构会造成重大损伤，提高阀芯可靠性意义重大。张任良等［4］通过对气-液界面亲水微通道减阻特性的影响进行研究，指出在宏观条件下，机构表面越光滑，流体流动阻力越小。王储等［5］对消防水炮射流轨迹理论模型进行研究，建立了同时考虑截面积修正系数和角加速度修正系数的空气阻力模型，对流体阻力的研究有一定的指导意义。陈海宏等［6］基于FLUENT 仿真模拟软件，研究造成分流型管汇偏流的主要原因。谢云杰等［7］基于CFD数值模拟对汇管出口流量分配对下游孔板流量计计量影响进行研究，结果表明，CFD 数值模拟可以有效获得孔板流量计内部的流场分布情况，并可根据具体的应用场合对孔板流量计进行标定。

综上所述，由于管汇系统由大量阀门和管路组成，阀门是其效能的关键部件，因此，提高关键部件的可靠性十分重要。将可靠性设计融入阀门设计中，通过优化阀芯结构，采用先进的数值模拟方法计算，并与理论计算结果进行对比，从而不断完善优化路径，提高初始空化值。同时降低外部声压级，能有效改善阀门内部的流动特性，使内部流场变得均匀而稳定，从而有效抑制空化现象，提高阀门可靠性。

1 阀门结构优化设计

阀门可靠性分析是在收集试验数据、分析失效机理和失效模式基础上进行的。Burmeister等［8］将阀门失效的原因归结为17种，主要失效形式有振动和噪声、夹紧停滞、泄漏、阀门工作压力波动、阀体破裂等。

在这些失效模式中，振动和噪声是影响阀门可靠性的重要因素。阀门产生振动的原因有以下4个：①介质流动过程中产生振动，使管道固定底座和阀门发生剧烈振动，从而导致阀门发生相应振动；②由于阀体内腔线性设计不良，导致介质流动不稳定时发生振动；③当介质流与阀门相互作用引起振动时，阀门过度节流导致涡流；④弹簧刚度过大或不足等也会引起振动。

由于这些因素与阀门设计、制造、使用等密切相关，决定了阀门的固有可靠性，而其他阶段只是尽可能地保持设计的固有可靠性。因此，为了提高阀门的可靠性，需从可靠性设计着手来优化设计，建立海底集管的故障树结构，提高故障树分析效率，识别集管系统中的风险点，优化关键部件，降低风险，提高系统使用寿命。

2 基于CFD的数值模拟分析

2.1 控制方程

流体流动受物理守恒定律支配。基本的守恒定律包括质量守恒定律、动量守恒定律和能量守恒定律。

质量守恒方程见式（1）。

动量守恒方程见式（2）。

能量守恒方程见式（3）。

球阀内部流场为不可压缩的三维黏性流，流体介质为室温20 ℃的水。基于不可压的雷诺平均方程组求解，采用标准k-ε双方程紊流模型构建封闭方程组。两种模型均采用二阶迎风格式离散，离散方程组的求解采用压力耦合方程组的半隐式方法（SIMPLE算法）。

2.2 边界条件

阀门数值模拟参数和工作参数见表1。模拟流道区域的入口位置为阀门公称直径的5 倍，出口位置为阀门公称直径的10 倍。采用结构与非结构网格有限体积法相结合的离散控制方程，自适应网格技术对模拟流场进行调整，使模拟流场精确网格总数大约为1.5×106个。

表1 阀门模拟参数

设定入口边界条件为速度入口，给定管道入口速度为0.25～6.00 m/s，共有23种不同流量，其间隔等差值为0.25 m/s。设定出口边界条件为压力出口，其值为0.1 MPa。计算时忽略重力对流场的影响。球阀的启闭属轴旋转结构，其开度为φ，取值为10°～90°，间隔值为10°。

2.3 结构模型

阀芯结构如图1所示，有三种类型：①阀芯A为普通阀芯，具有圆柱形流道；②阀芯B 为过渡型阀芯，弧形导流面结构；③阀芯C 为改进型阀芯，梳齿导流槽结构。

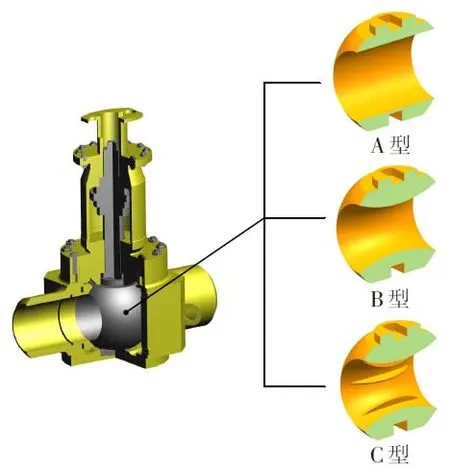
图1 三种不同结构的阀芯

阀门内部流道的截面如图2 所示，分别为x-截面、y-截面和沿流道中心线的c-截面。以阀门内部流道的截面来对其流动特性进行分析，从而反映流体在阀门内部流道的流动状态。

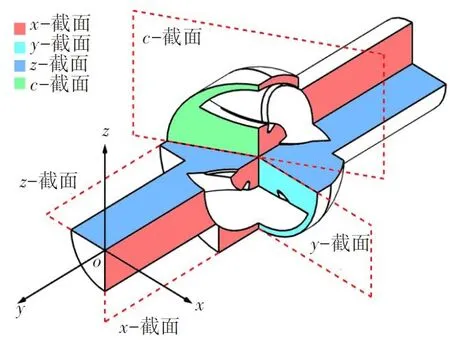
图2 阀门内部流场的三维截面

3 阀门数值模拟分析

3.1 阀门内部流场分析

本研究选取流速为3 m/s、开度在10°之间、流道内部变化较为明显的云图进行分析。阀门内部流场的CFD 模拟结果如图3 至图5 所示，其中，A、B、C 为阀门类型，x、y、z为阀门截面，数字为开度φ值。

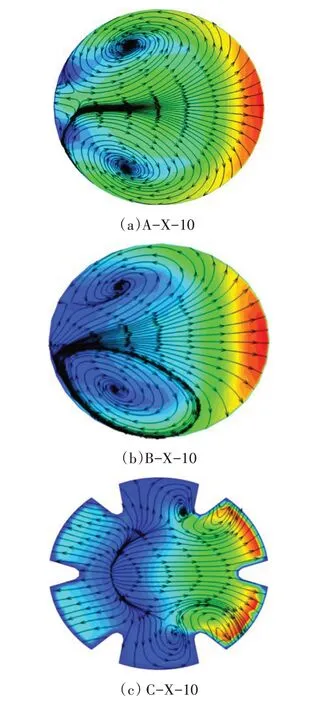
图3 流速为3 m/s下阀门内部流道x-截面的流场云图

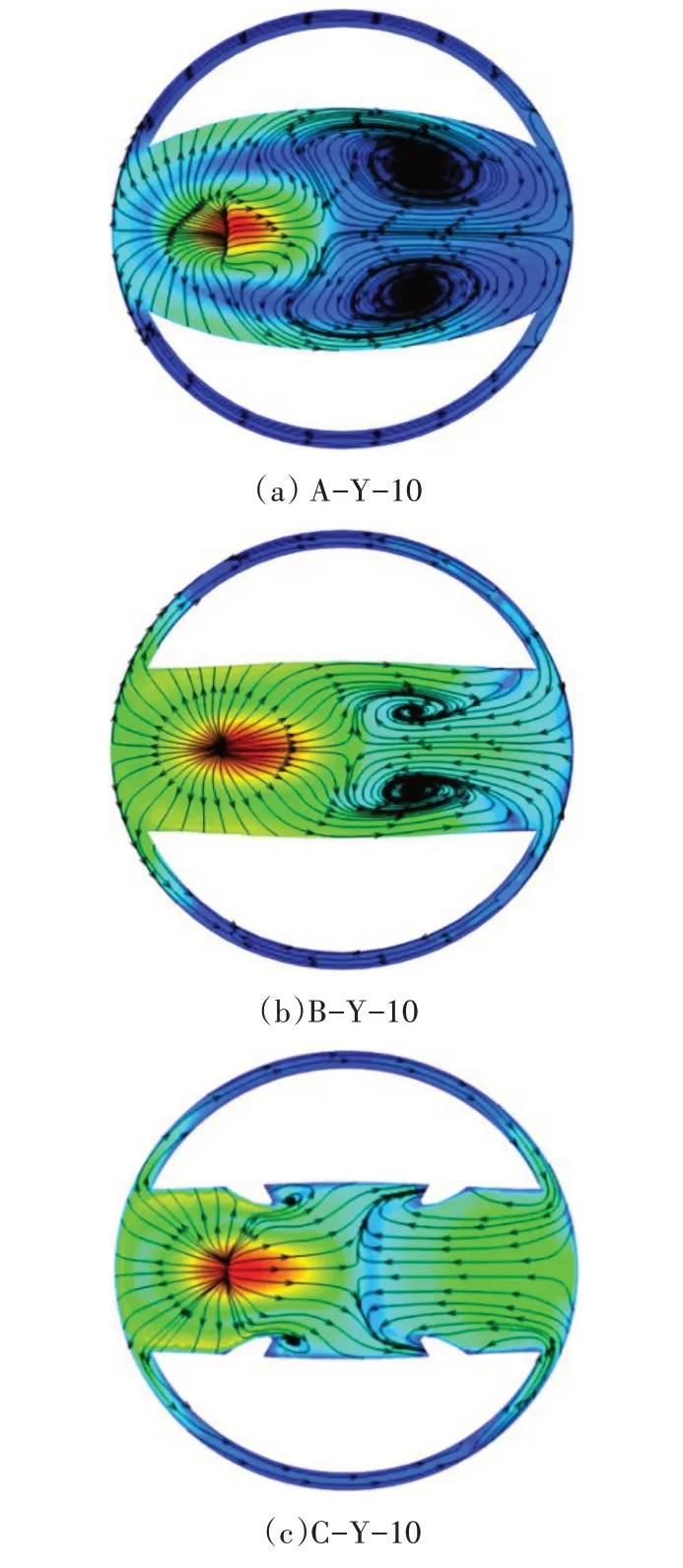
图4 流速为3 m/s下阀门内部流道y-截面的流场云图

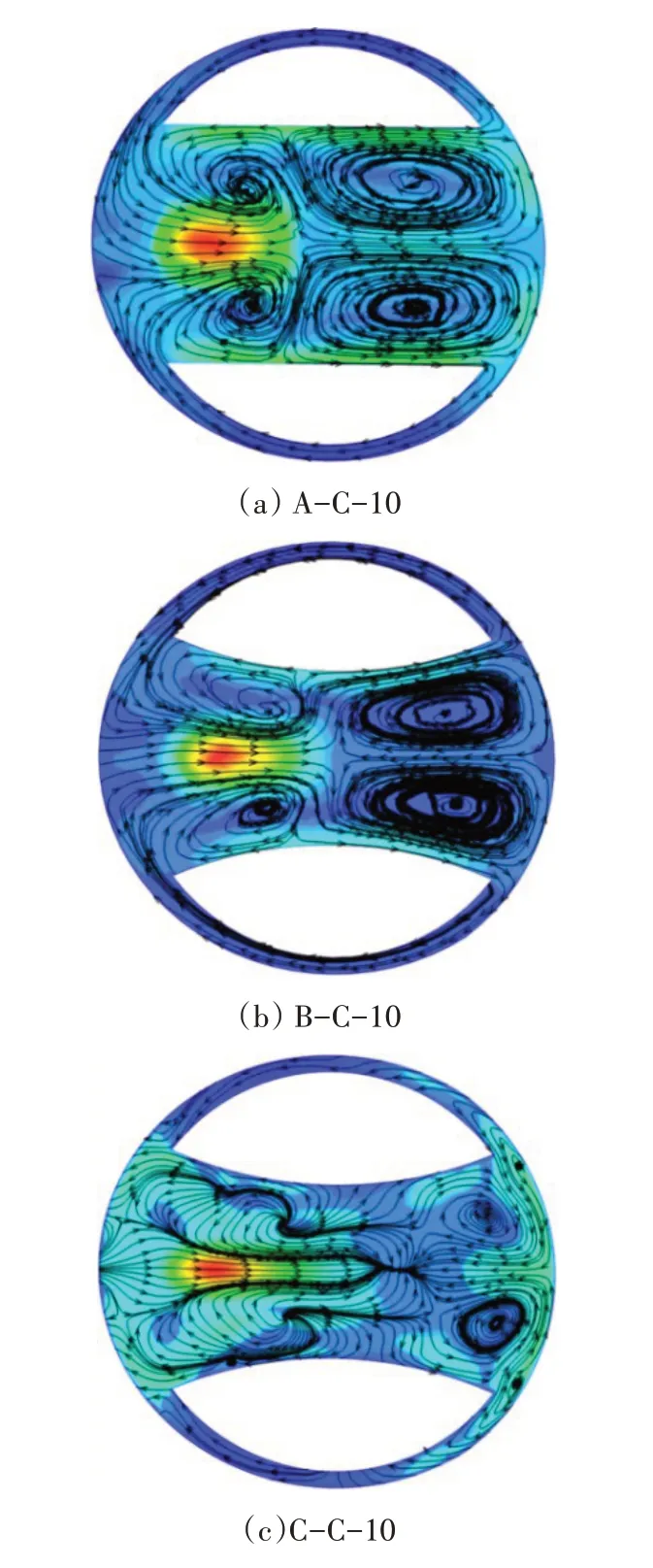
图5 流速为3 m/s下阀门内部流道c-截面的流场云图

从流场云图中可以看出，在相同流速、不同开度工况下，A 型阀门中存在低压回流区，并伴有大面积漩涡，表明流体的流动状态变化比较剧烈，高、低压过渡区不均匀。B 型阀门在小开度时存在高压和低压区，出现较大的漩涡区域，但随着开度的增大，该现象逐渐减弱。C 型阀门基本上不存在漩涡区域，没有明显回流区，流线比较均匀，说明介质流动相对稳定。通过对比分析可知：结构优化后的阀芯的内压力分布比较均匀，旋涡区域减小，甚至消失，流体在阀门内部的流动特性明显改善。

3.2 阀芯内部流动特性分析

管道内紊流或阀门内部流体空化现象均会产生噪声。通过测量液体动力流流经球阀产生的噪声及球阀下游和管道外部噪声级来预测空化现象。该方法中的重要参数有差压比xF、特性压差比xFz、修正特性压差比xFzp1和外部声压级LpAe。其中，xFz可有效评估阀门由紊流状态到空化状态时的初始值，是确定阀门产生噪声的关键参数，并以此确定阀门内部出现空化的状态，流体压差比xF和压差（P1-P2）、进口压力P1、出口压力P2及饱和蒸汽压力Pv，函数关系见式（4）到式（6）。

式（5）中进口压力为6×105Pa，如果需要进口压力，可根据式（6）对xFz值进行修正。

式中：N34为常数，其值表示流量系数（Kv或Cv）；Kv取值为1；Cv取值为1.17；Fd为阀门类型修正系数（无量纲）；FL为无附接管件控制阀的液体压力恢复系数（无量纲）。

当xF、xFzp1和∆p=(p1-p2)的数值确定后，可作为紊流状态和空化状态的判别条件。

紊流状态为∆p≤xFzp1(p1-pv)，即xF≤xFzp1。此时，外部声压级见式（7）。

空化状态为∆p>xFzp1(p1-pv)，即xFzp1

式中：Lpi为内部声压级；TLcav为空化条件下的传播损失；TLturb是紊流条件的传播损失。外声压级LpAe位于出口位置距离下游壁面1 m处的平面上。

在得到xF与LpAe的函数关系曲线后，采用确定xFz法能确定阀门空化现象和xFz初始空化值。该方法的理论计算值xFz与实际试验值基本一致，便于在选型计算中确定阀门是否发生空化，即阀门中xFz的值较高的情况，能更有效地降低阀门空化气蚀现象。

通过CFD 模拟结果，可以获得xF和LpAe之间的关系如图6 所示，C 面的二维显示如图7 所示。由图可知，三种不同结构的阀芯，以xF为参数确定的LpAe曲线基本相同，xFz值基本上位于同一点。

图6 Qm、xF和LpAe三者之间关系曲线

图7 基于xF的外部声压级LpAe曲线

三种阀芯构型的数值模拟结果见表2。通过对比可以发现，在开度φ 为45°、阀门为初始空化（xFz值）时，优化后的C 型阀门的xFz值比较大，外部声压级LpAe明显降低。C型阀芯的外部声压级LpAe值较A 型阀门有着显著降低，降幅为27.69%。C 型阀芯的初始空化值xFz为0.36，比A 型阀芯有效提高了0.09，比B 型阀芯提高了0.03。结果表明，改进后的阀芯对降低气蚀具有良好的改善效果。