次同步电流双通道附加阻尼抑制次同步振荡策略及阻抗模型分析

李博浩,郭昆丽,吕家君,蔡维正,白 阳,任蓓蕾,朱婷华

(1.西安工程大学电子信息学院,陕西省 西安市 710048;2.国网四川省电力公司乐山供电公司,四川省 乐山市 614000)

0 引言

近年来,直驱风机并网导致的次同步振荡问题对系统稳定带来的不良影响多有报道[1-5],针对其引发振荡的机理和抑制措施,国内外学者进行了广泛的研究。目前,针对次同步振荡机理的研究方法包括特征值分析法[6]、复转矩系数法[7]和阻抗分析法[8-9],文献[10-14]详细阐述了这3种分析方法的特点,并指出阻抗分析法是揭示风电并网诱发次同步振荡机理的主要方法并运用阻抗分析法揭示电网强弱对次同步振荡特性的影响。

针对弱电网影响的次同步振荡抑制措施,文献[15-17]提出采用自抗扰控制策略代替传统的比例积分(proportional integral,PI)控制策略抑制次同步振荡现象,但在实际应用时需要对控制系统做出修改,实施难度较大。因此,众多学者提出采用附加阻尼控制器抑制次同步振荡,附加阻尼控制器主要包含滤波器、相位补偿、增益和限幅环节;文献[18]指出风力发电机及其相关的控制参数发生变化时,会影响次同步分量的幅值与相位,增加实际工程中相位补偿环节参数的整定难度;文献[19]提出利用线路电流作为附加阻尼控制器的输入信号省略相位补偿环节抑制次同步振荡现象,但其主要针对单一振荡频率,若系统存在多个次/超同步振荡便会导致提取振荡频率不精确抑制效果不明显;此外,诸多研究表明运用阻抗分析法可以分析诱发次同步振荡的因素但是建立附加阻尼抑制策略阻抗模型并分析其稳定性的研究较少。

针对当前研究的局限,本文首先验证弱电网诱发次同步振荡的机理,提出一种弱电网下基于次同步电流双通道附加阻尼抑制策略并采用谐波建模方法建立该策略的阻抗模型。随后,进行稳定性分析为后文的仿真验证奠定理论基础,通过仿真验证本文方法抑制次同步振荡的有效性。

1 弱电网对次同步振荡的影响分析

用短路比(short circuit ratio,SCR)值λSCR描述电网强度,定义λSCR≤3的电网为弱电网,λSCR＜2的电网为极弱电网[20]。为验证弱交流电网是诱发次同步振荡的机理[21],分析PI控制方法下电网阻抗值对网侧变换器序阻抗特性的影响以及系统稳定性的影响,在0～50Hz的次同步频段内以及51～100Hz超同步频段内,电网阻抗分别取0.35 (λSCR=2.8)、0.48 (λSCR=2.1)、0.65mH(λSCR=1.5),参考文献[13-14]所建立的阻抗比矩阵的特征多项式,分别计算出PI控制下(无阻尼控制)阻抗比特征值并且绘制出Nyquist曲线图,如图1所示,其局部放大图如图2所示。PI控制(无阻尼控制)下电网电感为0.35 (λSCR=2.8)、0.48(λSCR=2.1)、0.65mH(λSCR=1.5)都包围了(-1,0)点,此时并网系统不稳定,极易诱发次同步振荡现象,从理论上验证出电网强弱是诱发次同步振荡的重要因素。

图1 PI控制下阻抗比特征值Nyquist曲线图Fig.1 Nyquist curve of impedance bit eigenvalues under PI control

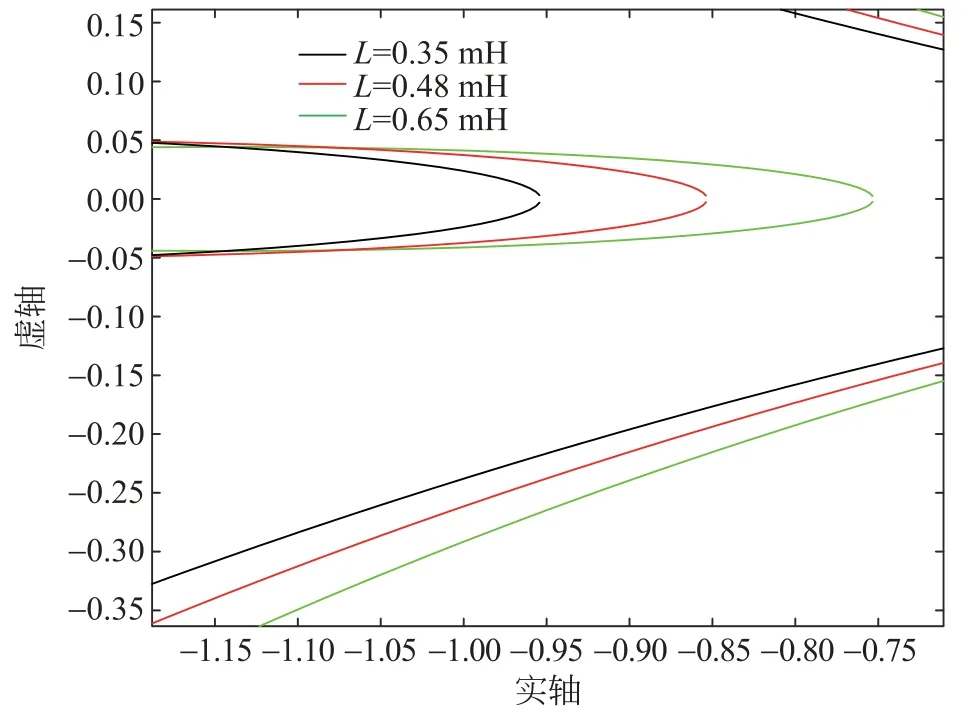
图2 PI控制下阻抗比特征值局部Nyquist曲线图Fig.2 Local Nyquist plot of impedance ratio eigenvalues under PI control

为进一步验证电网阻抗值增加对直驱风机并网系统稳定性分析的影响,在PSCAD 软件中搭建PI控制下不同的交流电网强度的仿真模型,仿真参数见表1。

表1 单台网侧扫频参数Table 1 Sweep parameters of single network side

图3(a)为电网电感L=0.35mH(λSCR=2.8)时的a相电流波形图,在3 s时投入0.35mH 的电感,此时系统接入弱交流电网,电流波形开始振荡,由图3(b)可知PI控制下电流存在22.73Hz和77.27Hz的次/超同步分量。图4(a)为电网电感L=0.65mH(λSCR=1.5)时的a相电流波形图,当系统运行至3s时投入0.65mH 的电感,此时系统接入弱交流电网,系统迅速出现振荡现象,由图4(b)可知,在λSCR=1.5时也存在5.13/94.87、27.6/72.4Hz这2组次/超同步频率分量。根据上述分析可知,验证了图1的理论分析,在弱电网情况下极易诱发次同步振荡现象。故后文是以弱电网的情况下展开研究。

图3 L=0.35mH(λSCR=2.8)时的a相电流Fig.3 A-phase current analysis diagram when L=0.35mH(λSCR=2.8)

2 弱电网下基于次同步电流附加阻尼抑制策略分析

由于次同步振荡现象主要是网侧变换器及其控制系统与并网系统动态交互引起,故将风力机、永磁同步发电机及机侧变换器等效为受控电流源[16]。本章基于前文分析,设计出一种基于次同步电流双通道附加阻尼抑制策略,如图5所示。

图5中:U、I为网侧变换器三相输出电压和电流;Upcc、Ipcc为并网点电压和电流;Udcref、Ipdref和Ipqref分别为系统直流侧电压参考值、控制器dq轴电流参考值;Udc为系统直流侧电压;Iz、If分别表示为等效受控直流电流源和直流侧输出电流;Cz为直流侧电容;Lp为滤波电感;L为网侧电感;α表示为锁相环输出相角。

2.1 附加阻尼抑制次同步振荡机理

根据文献[17,21]可知,当接入弱交流电网时,在PCC点处产生次/超同步电流,进一步在并网点形成次/超同步电压。电流内环PI感到变化后输出次/超同步电压分量,从而产生新的次/超同步电流分量。新的次/超同步电流与原有的次/超同步电流形成正反馈,使得振荡增强,导致整个系统失稳。当系统发生次同步振荡现象,并网点处电流Ipcc中既存在50Hz的工频分量也存在次/超同步分量。采用带通滤波器从Ipcc提取出次/超同步分量经过增益环节和限幅环节后,得到抑制次同步振荡的电压参考指令信号Uci;该指令信号与电流内环PI感到变化后输出的次/超同步电压信号U'相位相反,使得网侧变换器输出电压U上不存在次/超同步分量,从而破坏新的次/超同步电流的形成,实现对次同步振荡的抑制。通过上述分析,阻尼环节抑制次同步振荡的机理过程并未涉及到风电机组及其控制器,因此无需考虑相位补偿以简化附加阻尼控制环节的设计。

2.2 附加阻尼抑制策略参数设计

本文所提出的附加阻尼环节包含带通滤波器,增益环节和限幅环节。

2.2.1 带通滤波器

采用二阶Butterworth带通滤波器,传递函数为

式中:ωn=2πfn,fn为目标频率;ζ为阻尼系数,其设置为0.707。

结合本文第1章节分析,主要考虑5.0～27.6Hz的次同步分量和60.00～94.87Hz的超同步频率分量。本文在设计参数时分别选取27.6和94.87Hz作为次/超同步通道的目标频率,将数值带入式(1)中绘制其伯德图如图6所示。

图6 针对27.6/94.87Hz频率带通滤波器伯德图Fig.6 Bode plot for 27.6/94.87Hz bandpass filter

由图6可知,带通滤波器可有效提取次/超同步频率分量,同时27.6/94.87Hz对应的相位为0°,可见本文设计的滤波器具有最佳的相频特性,进一步说明无需考虑相位补偿环节;而且滤波器带宽能够躲开其余频段不受影响,满足设计要求。

2.2.2 增益环节

附加阻尼控制环节对次同步振荡的抑制效果不仅与输入信号的选取,滤波器的设计有关,增益环节K主要是为了产生合适的次同步电压信号。本文对K的选取采用时域仿真测试法,K=2。

2.2.3 限幅环节

限幅环节可以限制输出信号的幅值,保证输出的信号大小在限定范围之内。本文限幅环节的取值为±20。

3 弱电网下基于次同步电流附加阻尼抑制策略阻抗建模及稳定性分析

为进一步分析本文所提出的抑制策略稳定性,本文建立序阻抗模型由主电路、锁相环、电压电流双闭环以及调制环节组成。根据图5可知,本文提出的附加阻尼抑制策略信号是叠加在网侧变换器三相输出电压上故对调制环节数学模型的建立产生影响,而主电路、锁相环、电压电流双闭环3个环节的推导过程和结果详见文献[13-14]。下文推导调制环节的数学模型。

3.1 阻抗建模

网侧变换器a相出口的输出电压为

而不采用次同步双通道附加阻尼控制网侧变换器a相出口的输出电压为

式中:km为调制系数;Ma为a相调制信号;Gn1(s)、Gn2(s)分别代表次/超同步传递函数,即

式中:ωn1=2πfn1,ωn2=2πfn2,fn1、fn2分别代表次/超同步通道的目标频率;ζ1=0.707、fn1=27.6Hz;ζ2=0.707、fn2=94.87Hz。

对式(2)进行傅里叶变换和应用卷积定理[22],得到网侧变换器a相输出端口的频域表达式:

式中:U1、f1表示基频电压幅值和频率;I1表示基频电流幅值;M1=(U1+j2πf1LpI1)/(kmUdc0);为其共轭;Udc0为直流侧电压的给定值;Ip、In分别表示为正序、负序的扰动电流幅值;fp、fn分别表示为正序、负序的扰动频率幅值。

根据文献[20]得到网侧变流器次同步振荡的导纳模型:

式中:δ(s)=Gn1(s)+Gn2(s);θ=I1(Gn1(s1)+Gn2(s1))+Udc0Hv(s1)Hi(s1);E为单位阵;Hi、Hv为电流内环和电压外环控制器的传递函数;Kd是解耦增益系数。

根据频率耦合特性关系图[14],建立正负序导纳模型和阻抗模型分别为

式中:Y11(s)和Y22(s)为自导纳;Y12(s)和Y21(s)为互导纳。

为了验证建立的序阻抗解析模型的准确性,利用扫频法得到仿真测量的导纳模型,参数见表1,仿真结果如图7所示。图中:红线表示解析导纳模型,蓝色点代表仿真测量得到的导纳点。由图7可知,解析导纳曲线和仿真测量的导纳点可以很好的吻合。进一步说明本文建立的阻抗模型的准确性并且能够较好地描述网侧变换器的频率特性。

3.2 稳定性分析

为分析双通道附加阻尼控制方法下,电网阻抗值对网侧变换器序阻抗特性的影响以及系统稳定性的影响,电网阻抗分别取0.35 (λSCR=2.8)、0.48(λSCR=2.1)、0.65mH(λSCR=1.5),带入序阻抗解析表达式,得到次同步双通道附加阻尼网侧变换器阻抗与电网阻抗伯德图,如图8所示。图8中随着电网阻抗增大,50Hz频段附近的阻抗幅值减小,在5.0～27.6Hz的次同步频段内以及60.00～94.97Hz超同步频段内,电网阻抗的幅频特性与网侧变换器幅值没有交点,不存在次同步振荡风险。

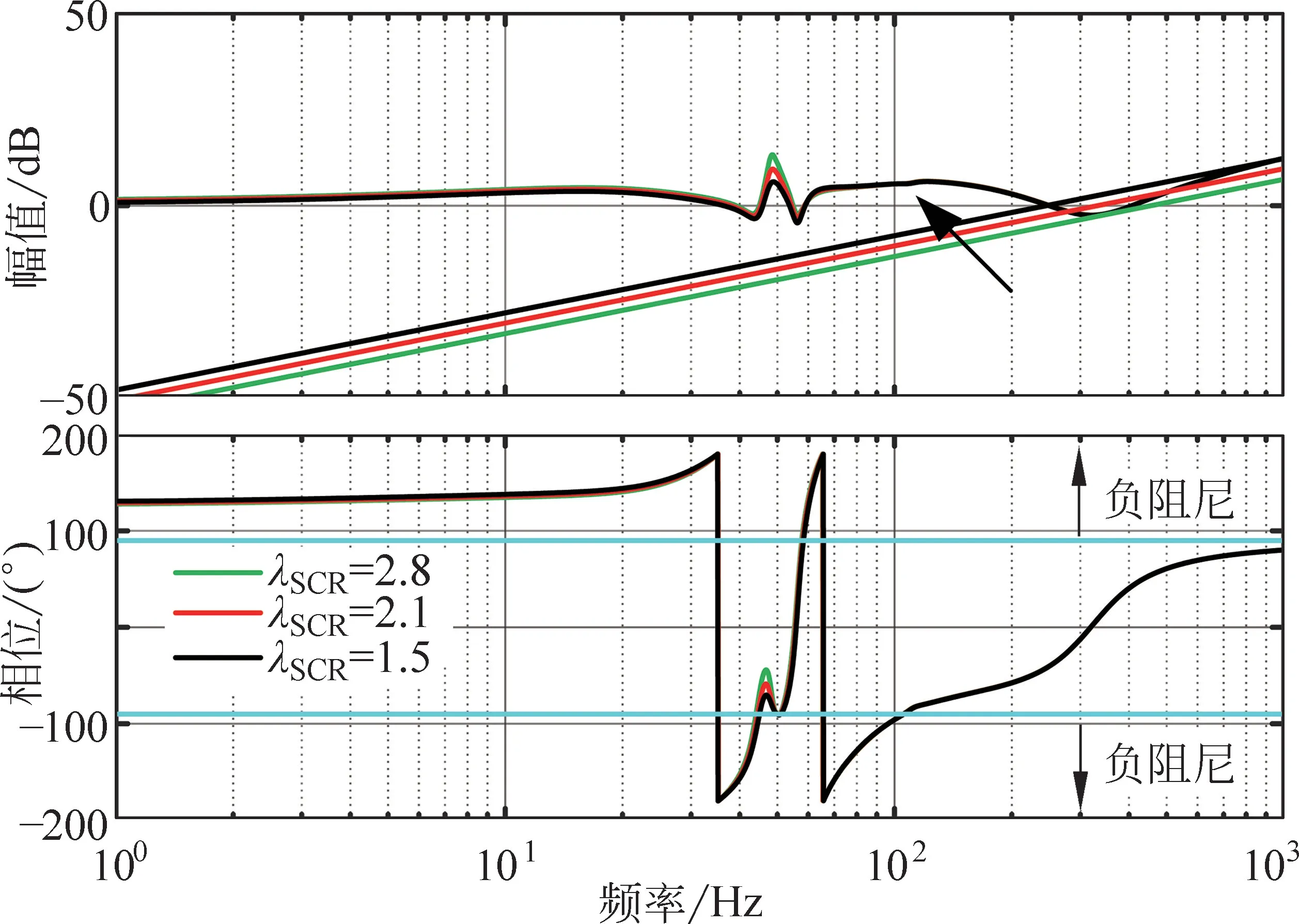
图8 次同步双通道附加阻尼网侧变换器阻抗与电网阻抗伯德图Fig.8 Simultaneous two-channel additional damping grid-side converter impedance and grid impedance Bode plot

下面定义阻抗比矩阵L(s)=Yo(s)Zg(s),其表达式如下[22-23]:

列写阻抗比矩阵的特征多项式:

根据式(15)求取特征值为

为验证附加阻尼控制策略稳定性根据式(16)绘制出附加阻尼控制策略下阻抗比特征值的Nyquist曲线图,如图9所示。与图1对比发现曲线不包围(-1,0)点,提升了并网系统稳定。为后文的仿真验证奠定理论依据。

图9 附加阻尼控制下阻抗比特征值Nyquist曲线图Fig.9 Nyquist curves of impedance bit eigenvalues under additional damping control

4 仿真分析

为验证本文所提出的控制策略抑制次同步振荡的有效性,根据图5在PSCAD/EMTDC仿真软件中搭建仿真模型,仿真系统参数见表1。

算例1:设置风速为8m/s,3s时接入电网电感L=0.35mH (λSCR=2.8);投入电网电感后,风电机组直流侧电压出现次同步振荡现象。3种控制策略对比分析仿真结果,如图10(a)所示。

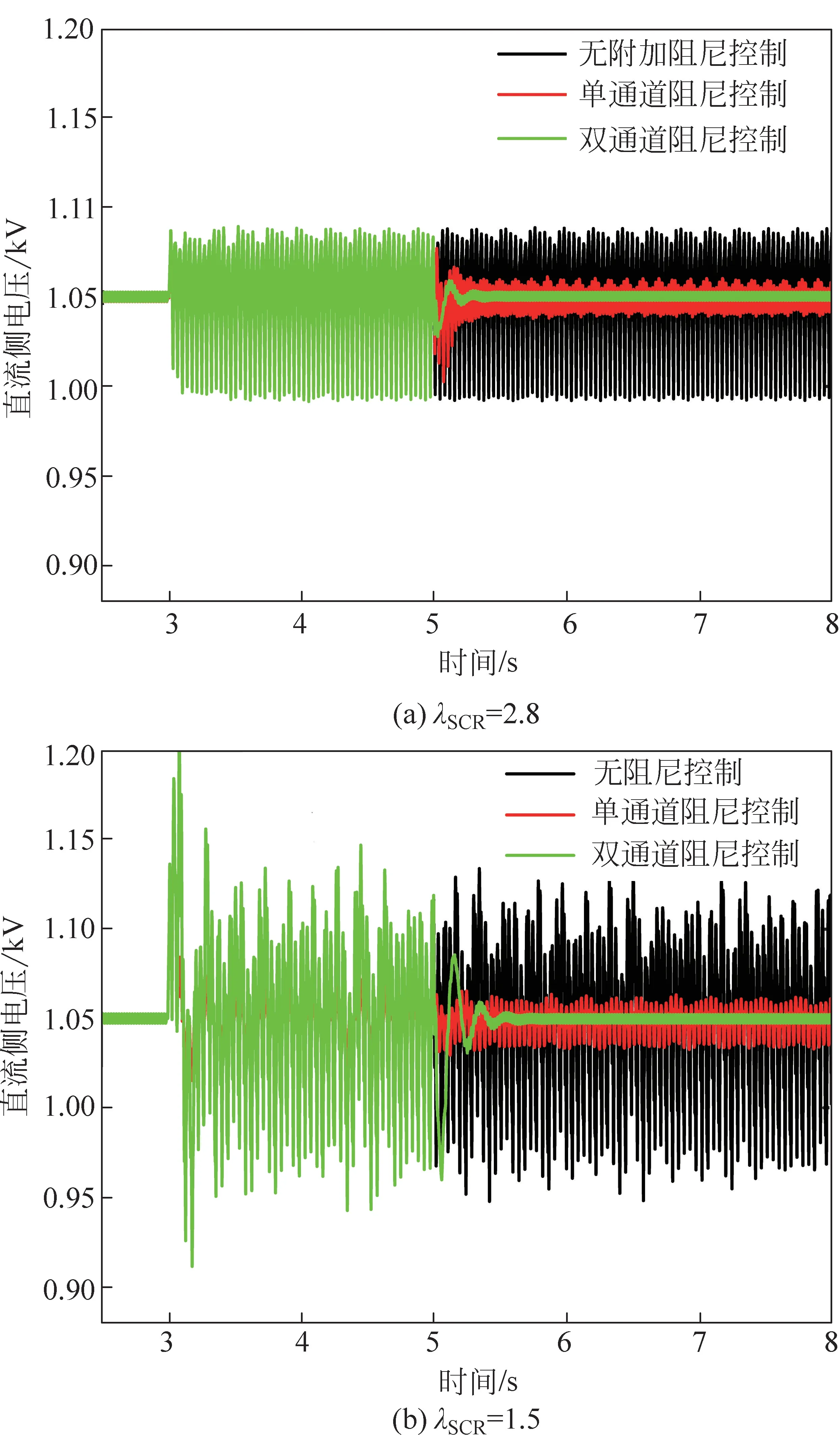
图10 不同短路比的抑制效果Fig.10 Suppression effect of different short-circuit ratios

算例2:设置风速为8m/s,在3s时投入电网电感L=0.65mH (λSCR=1.5),风电机组直流侧电压,出现次同步振荡现象,3种控制策略对比分析仿真结果如图10(b)所示。

由图10所示,在t=3s时,电网电感接入;无阻尼控制下网侧变换器侧输出的直流侧电压迅速振荡,引起系统不稳定,发生次同步振荡现象。在t=5s采用单通道附加阻尼控制策略,由于忽略了多个次/超同步振荡情况提取振荡频率不精确,导致系统直流侧电压进入稳态时存在着较大的波动,使得抑制效果不明显。而采用本文的策略的波动范围相较于无阻尼控制和单通道附加阻尼控制有所减小,波动范围见表2。

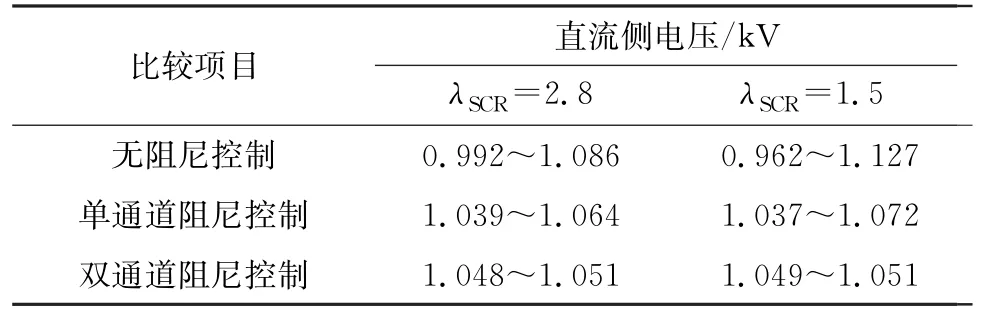
表2 控制波动范围Table 2 Control the fluctuation range

在2种不同短路比情况下,采用本文抑制策略对a相电流进行FFT 分析后,如图11—12所示。与图3—4对比发现,a相电流都仅有50Hz的工频分量,下面对抑制机理进行验证,验证图如图13所示。

图11 采用次同步电流双通道附加阻尼控制后的a相电流(L=0.35mH、λSCR=2.8)Fig.11 The A-phase current which is controlled by secondary synchronous current dual channel with additional damping when L=0.35mH and λSCR=2.8

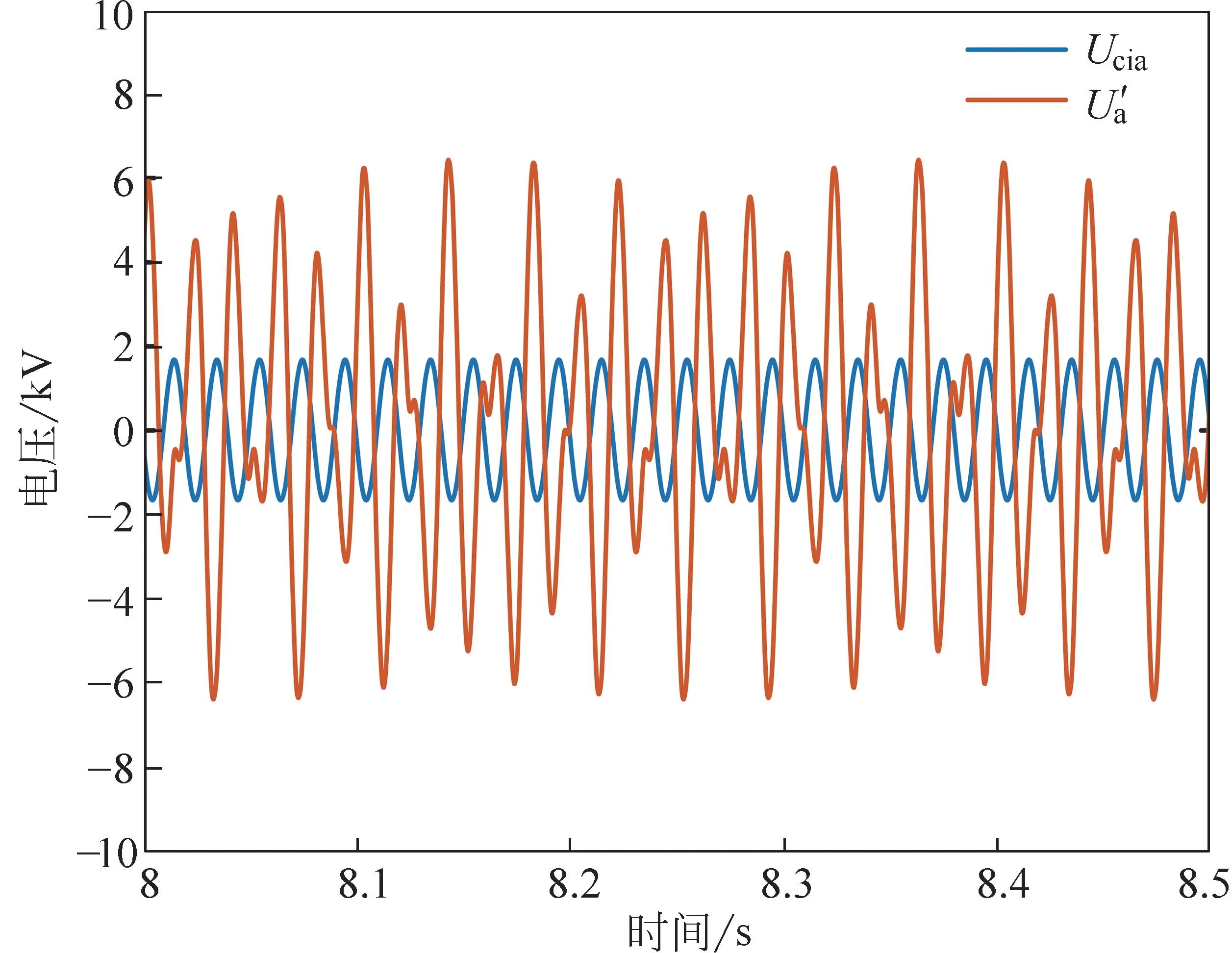
图13 机理验证图(以a相为例)Fig.13 Mechanism verification diagram

根据图13可知,运用本文所提出的附加阻尼抑制策略所得到的电压参考指令信号Uci与电流内环PI感到变化后输出的次/超同步电压信号U'相位相反,验证了本文节理论分析。通过上述分析本文所提出的抑制策略可更加有效地抑制次同步振荡现象并且具有较好的适应性。

5 结论

(1) 通过推导双通道附加阻尼控制阻抗模型,从理论上验证本文提出策略的有效性。

(2) 仿真结果表明相较于无附加阻尼控制和单通道附加阻尼控制,本文所提出的策略可以减小系统跟踪误差波动的同时在多种工况下可以更加有效地抑制次同步振荡现象。