高速动车组仿真驾驶软件的优化设计
2024-01-16刘诗佳
刘诗佳
(1 北京纵横机电科技有限公司,北京 100094;2 中国铁道科学研究院集团有限公司 机车车辆研究所,北京 100081)
高速动车组的设计和运营是非常复杂的系统工程。因此,借助电子计算机的高速和精准运算能力,提前分析并提高动车组在轨道线路上的运行效率,对提高运营效果尤为重要。
虽然国外先于我国开展高速动车组仿真平台的研究,例如北美的RAILSIM、欧洲的TRAINSTAR、日本的UTRAS[1]、俄罗斯的EMUTTCS[2]。与此同 时国内不少机构也展开了符合我国国情的高速动车组仿真系统的研究开发。中国铁道科学研究院集团有限公司机车车辆研究所开发了高速动车组牵引制动仿真系统[3],使用动车组的动力学模型推算动车组的运行状态[4],提供了方便直观的动车组控制系统,还绘制了轨道线路纵断面的细节[5-6]。
以上仿真系统大多为离线仿真。为了将仿真系统用于指导司机实际操作,就需要对仿真系统进行优化,提高其运行效率以便及时为司机控车给出正确精准的指导。文中从仿真系统数据结构角度出发,提出优化方案,同时提出高速动车组的能耗计算解决方案,为进一步研究和对比节能控车策略,提供了帮助。
1 辅助驾驶系统需求
高速动车组辅助驾驶系统的目的,是为了给司机提供控制高速动车组行进速度的操作指令序列,如在什么时间或位置,将控制手柄具体放在牵引、制动、惰行或定速中的哪个档位上。确保在这些操作建议都顺利执行的情况下,高速动车组能按照时刻表准时到达每个停车站,同时所消耗的电能尽量少,并提高旅客的舒适感。这些高速动车组操作指令序列,将成为未来高速动车组全自动驾驶系统的重要基础。
1.1 灵活的配置
文中使用的仿真系统在文献[3]中有所描述,以其中的基本参数配置为基础,对具体数据结构、有关配置界面进行了功能补充和性能优化。
首先,对高速动车组特性曲线的计算补充了散点描述方式,当没有合适的公式来描述对应曲线时,我们用“线性平均值”算法基于速度来推算所需数值,如图1 所示。
其次,补充和完善了以下配置及参数:
(1)时刻表及模拟乘客上下车后车重变化情况,让仿真过程更加贴近实际运营情况,其配置如图2 所示。

图2 配置时刻表及模拟停车站上下车情况
(2)分相偏移、车站限速、轨道限速偏移等配置,让仿真过程更加贴近司机在区间运行控车时的实际操作,如图3 所示。

图3 配置相关的偏移参数
(3)模拟司机加速和减速的操作特性,设置界面如图4 所示。通过在低速阶段限制牵引电机发挥牵引力的比例,保证规划和仿真时,最大程度上贴近司机操作高速动车组进出站时的实际情况。

图4 高速动车组加速和减速策略配置
1.2 有限的计算资源
作为车载系统的辅助模块,其能够使用的资源有限。让辅助驾驶系统每次都能迅速地完成规划,并给司机提供准确的辅助驾驶信息,要对其数据进行优化,减少数据量。
为实现快速规划,在现有仿真平台的基础上,对仿真系统的数据结构进行重点优化设计[3]。
2 辅助驾驶系统优化设计
首先,优化轨道数据的记录结构,并对应优化仿真结果记录算法,实现提高辅助驾驶指令序列规划的及时性、降低数据量的目的。然后,设计了能耗拓扑图功能,通过描述电能传输路径及各电能传输节点的传输效率,计算该能耗拓扑结构所在车型运行时所产生的能耗。
2.1 轨道数据结构优化
轨道在建设施工时通过“公里标+本段轨道长度”描述。但是,后续由于种种原因对实际轨道进行维护更新之后,一些轨道分段长度会发生变化,由此产生“长短链”的情况。即有些轨道区段的长度,不同于2 个相邻公里标的差值。例如,某条轨道线路上公里标1.1~2.2 之间的轨道区段,长度为800 m,而不是公里标的差异1.1 km,这种情况就是“短链”,反之为“长链”。
“长短链”的存在导致高速动车组运行的实际距离不同于轨道上的公里标,容易引入误差,导致程序运行混乱。为此提出以下优化手段:
首先,用“绝对位置”替换“公里标+本段轨道长度”记录轨道数据,并定位高速动车组在轨道上的位置。绝对位置,以轨道线路的起点为位置0,轨道上每个点的位置,以动车组从位置0 行驶到该位置时,实际行驶的距离标注。这个数值向轨道终点方向递增,与轨道是上行还是下行无关。
通过转换,轨道线路上的每个点都有了唯一的“绝对位置”,且跟原本的“公里标+本段轨道长度”相互转换、一一对应。“绝对位置”递增或递减的距离,对应高速动车组前进或后退时移动的实际距离,这样可以极大地简化动车组所在位置的相关运算。
其次,轨道的数据由坡度、曲线、桥隧、分相位置4 个列表组成。坡度记录轨道每个区段的起点公里标、长度、坡度值,以及停车车站的站中点;曲线记录轨道所有曲线的开始位置、曲线半径、曲线长度等;桥隧记录轨道线路经过的所有桥梁、隧道的公里标和长度;分相列表记录轨道分相开始和结束的位置,在分相路段内,高速动车组失去电力供应,被迫惰行。
将以上4 个列表的每个分段开始和结束位置,都转化为“绝对位置”记录后,把这些分段的点合并为一个“轨道描述列表”。这个列表的每一条都记录了一段轨道的参数,包括坡度、车站、曲线、桥隧、分相等参数,确保在同一条记录描述的轨道长度内,这些参数不会变化。
仿真时,只要高速动车组在“轨道描述列表”同一段轨道内运行,就不必重复查询轨道参数,且来自轨道的阻力为恒定值。如果高速动车组为恒速运行,则其风阻也是恒定的,那么对应的手柄控制就是固定的。在该段轨道内运行状态的描述就可以极大地简化。
2.2 仿真结果优化
文献[3]中描述的散点方式记录高速动车组的运行曲线。每个数据点记录了高速动车组在轨道上的位置、车速、时间、手柄位置、加减速相关的力学参数及轮周功率等数据。
但是,文献[3]中使用固定的时间间隔(如0.1 s)生成记录,导致2 个问题:其一,当2 个数据点之间存在变坡点的时候,坡度变化引入误差,且该误差在不断地积累;其二,数据点过多,即便高速动车组以350 km/h的速度运行,每公里也需要至少102个节点,以武汉到广州约1 100 多公里的线路为例,整条线路仿真数据点超过11.3 万个,如此多的数据点显然会减慢有关数据的处理速度。
文中提出如下步骤对数据进行优化。
首先,将仿真结果中的节点位置,与“轨道描述列表”中的节点对应。规则如下:
(1)如果动车组在一个路段内恒速运行,则只需一个对应该路段起点位置的数据点记录有关状态,因为在同一个路段内高速动车组的控制参数和运行状态一样。
(2)如果动车组在一个路段内无法保持恒速运行,则2 个数据点之间的时间差以固定时间间隔记录,如0.1 s。但是,如果下一个数据点的位置离开了当前路段,则重新定位下一个数据点,将其定位到下个路段开始的位置。
其次,对于轨道线路中会重复使用的曲线序列,提前进行计算的时候也遵循以上规则。这些曲线序列包括:停车车站的进站停车曲线、出站发车曲线、分相惰行区域的强制惰行曲线、可能超速路段的提前减速曲线。由于加速策略和减速策略在配置中指定,不论后续的曲线优化执行多少次,以上这些曲线在最贴近限速驾驶的情况下,都是固定的。仿真系统提前计算一次,后续遇到的时候直接复制这一段曲线数据,即可极大地减少实时规划时间。
通过以上两步优化,可以大量削减描述仿真结果的“位置—速度曲线”所需的数据点总数,提高计算效率。
2.3 灵活的能耗计算
辅助驾驶的重要功能之一是节能,这需要能耗计算为基础。但不同高速动车组内部对于电力的使用方式不尽相同,如果针对每个车型单独编程计算其能耗,会极大地增加编程工作量,且灵活性不足。
优化设计就是增加电能传输拓扑图功能。通过描述高速动车组内部电能传输的拓扑结构,灵活准确地计算其能耗,如图5、图6 所示。
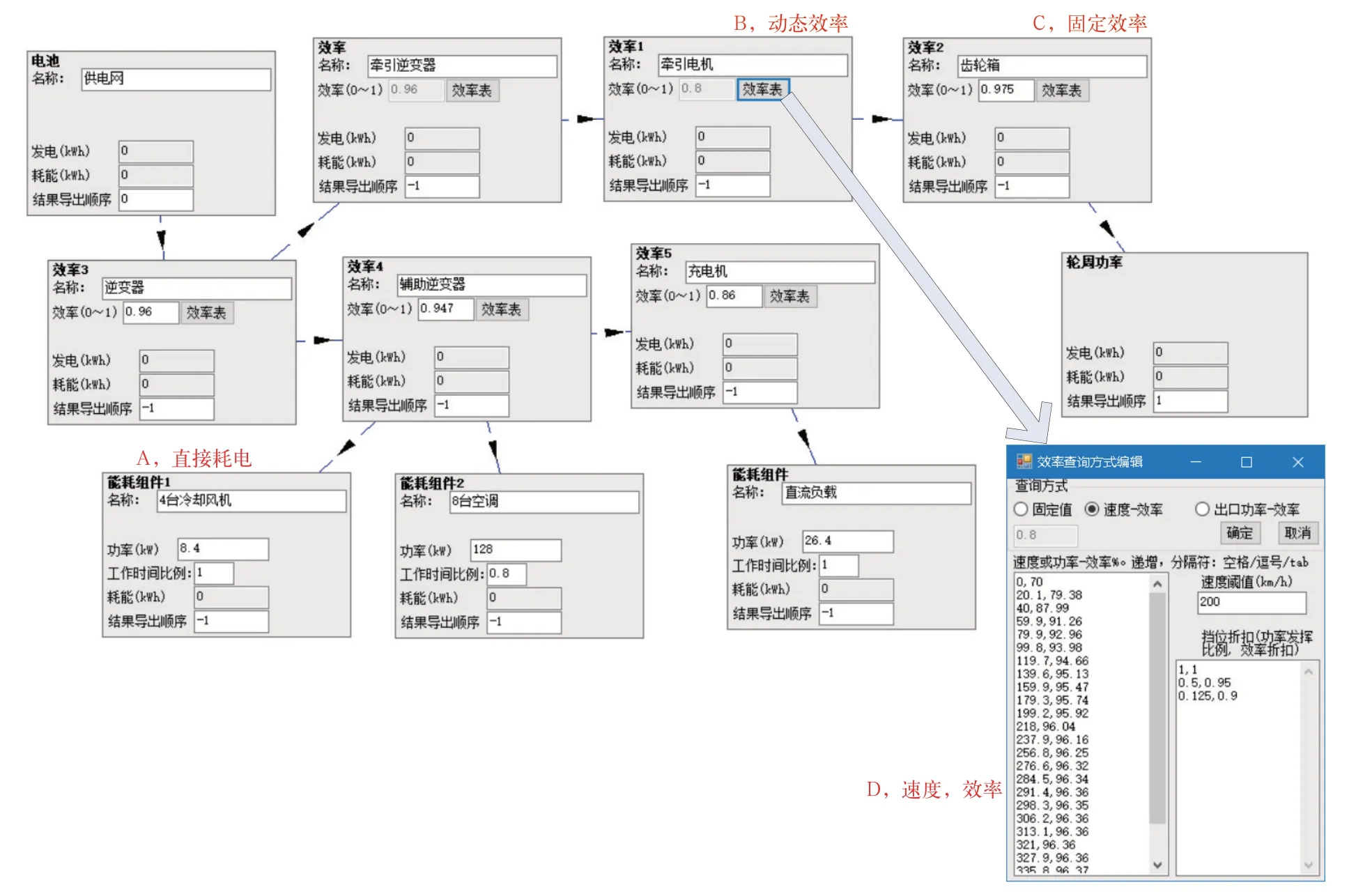
图5 电能拓扑图方案1
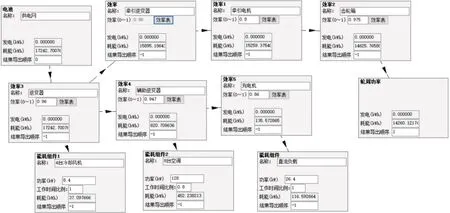
图6 电能拓扑图方案2
图5 中描述了一种能耗拓扑结构。每个方块为一个能耗节点,“节点类型+编号”在方块左上角粗体字标注,节点可设置不同名称,效率类型方块可设置不同的电能使用效率参数,如“效率1”(图中红色文字标注“B,动态效率”)方块的效率为根据速度而变化的(其具体变化规律见红色文字“D,速度,效率”标注处),而“效率2”(图中红色文字标注“C,固定效率”)方块的效率为不随速度变化的固定值。“能耗组件”为直接耗电的模块,如冷却风机(图中红色文字标注“A,直接耗电”)、空调等;“轮周功率”为高速动车组在不同速度下的牵引系统传递到驱动轮上发挥出的功率。整个能耗拓扑结构,用箭头连接各个方块来描述:电能从供电网,经过各种能量转换节点,传送到各个耗电方块的过程。
在图6中,描述了另一个型号的高速动车组内部能耗拓扑图,与图5 中的差异体现在“能耗组件1”的电力来源不同,以及“效率1”的效率从随速度变化改为固定值。
能耗计算的过程,就是通过这个拓扑结构,从“轮周功率”和各“能耗组件”,沿着能耗拓扑的路线倒推,计算出不同速度下,高速动车组从供电网获得的总功率,再按照时间积分得到总能耗。计算过程中,正数表示耗电量,负数表示再生制动的发电量,可以分别计算出来。
高速动车组仿真运行的每个数据点,都有速度、手柄、牵引力等参数。根据速度和牵引力,可以算出每个数据点处高速动车组车轮上的功率,即“轮周功率”。轮周功率乘以时间得到车轮能耗,通过对能耗拓扑图的逆向推导,可以得到高速动车组从供电网上获取的电能。再对运行曲线上所有节点的能耗进行积分,就可以累计出高速动车组运行过程中消耗的电能,以及再生制动生成的电能。
能耗计算时,如果不考虑能耗拓扑结构,则计算出的能耗会远小于实际能耗,因为每个电能的转换节点都会产生额外能耗,而且这个额外能耗会根据速度、运行距离的不同而产生显著变化。
没有以上能耗拓扑图功能的仿真软件,为了准确计算不同车型的能耗,需要根据每个车型的能耗拓扑图进行单独编程,这会大大增加软件的规模和出错的概率。
3 仿真结果
以某线路及某高速动车组车型为例,按照时刻表的出站和到站时间为标准,进行仿真运行。将对比数据点个数、精准停车、能耗计算这几个方面。
高速动车组运行曲线记录的数据点个数优化前后对比,如图7、图8 所示。在这2 个图中,左侧为速度轴,下部为轨道线路参数,包括坡度、曲线,上部为图注,中部为限速、分相、车站、位置—速度曲线。其中,“位置—速度曲线”以散点表示。图中的路段为某站到公里标1 273.6(这也是一个变坡点)这段区间内的“位置—速度曲线”。

图7 优化前“位置—速度曲线”上的数据点分布

图8 优化后“位置—速度曲线”上的数据点分布
优化前的“位置—速度曲线”数据点体现在图7中,优化后的“位置—速度曲线”数据点体现在图8 中。可见,在某站到公里标1 273.6处,优化前的数据点上百个,而优化后的数据点只有1 个。此外,在某站左侧的数据点对比中,优化后的数据点比优化前同样大幅度减少。
精准停车方面,优化前后的“位置—速度曲线”对比如图9、图10 所示,其中用颜色标注了高速动车组的运行状态,粉色为制动,蓝色为牵引,绿色为惰行。
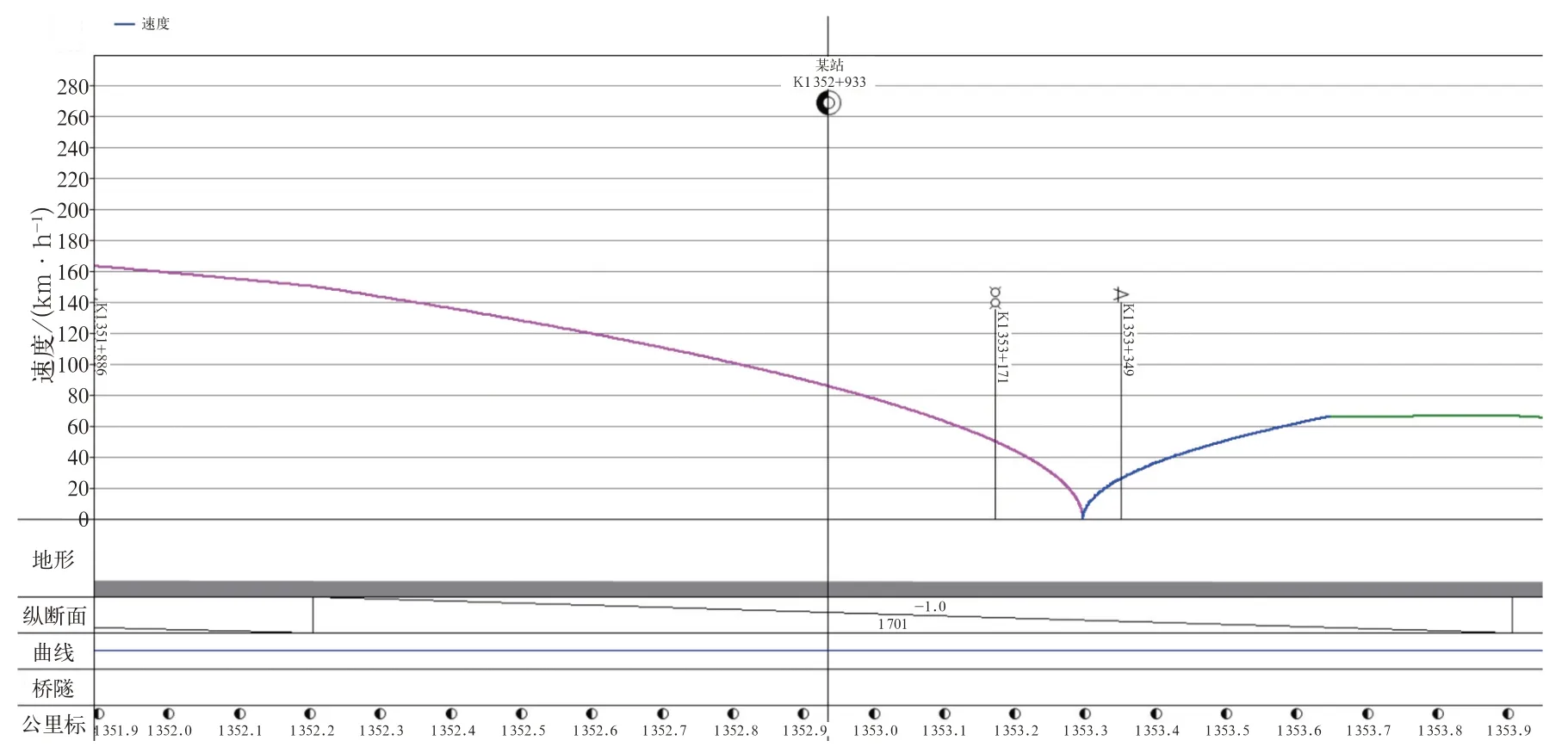
图9 优化前“位置—速度曲线”的停车误差

图10 优化后“位置—速度曲线”的停车误差
优化前的停车位置如图9 所示,停车存在大约300 m的误差。优化后的停车位置如图10 所示,停车误差几乎不可见。
能耗计算时,使用图5 和图6的拓扑结构会产生不同的总能耗。使用图10 中的“位置—速度曲线”数据,按图5的电能拓扑方案计算的总能耗为17 244.86 kW⋅h,而按图6的电能拓扑方案计算的总能耗则为20 522.68 kW⋅h。
4 结论
通过以上仿真对比分析,可以看到优化后的高速动车组辅助驾驶系统实现了既定目标。
通过轨道数据记录的优化设计,并对应调整算法,确保仿真结果数据点大幅度减少;由于“位置—速度曲线”的数据点能对应上“轨道描述列表”中的数据点,停车位置更加精准。
通过能耗拓扑图功能,不必根据每个车型重新编码,而只需根据车型构建能耗拓扑图,从而极大地减少了编码工作量。这样,不但可以灵活准确地计算不同控车策略产生的能耗,还能方便地对比不同车型产生的能耗差异。
实现了这些优化之后,后续可以进行基于能耗优化的控车策略研究。
