朔黄铁路重载列车试闸与制动力判断标准研究

刘博阳，魏伟，豆飞

（1 大连交通大学 机车车辆工程学院，辽宁大连 116028；2 国家能源集团朔黄铁路机辆分公司，河北肃宁 062350）

由于重载铁路绿色环保、节能高效，自20 世纪50 年代起，在世界范围内开始迅速发展，重载运输里程持续增长，但由于重载列车发车间隔短、编组长、质量大，加之线路条件复杂多变，重载列车运行安全问题仍不容忽视，同时也给司机平稳操纵和列车准点运行带来极大挑战。

为探明重载列车运行特征和相关特性，实现安全平稳运行，国内外学者通过试验或仿真方法开展了系列研究，并且随着科技的高速发展，计算机仿真计算凭借可选择方案多、风险小、成本低以及可获取某些参数微小差异的影响等优势，成为重载列车相关研究的高效率、高质量解决方案，目前可通过采用商业软件或自主建立仿真模型2 种方式实现仿真计算［1］。Ansari 等基于非线性时域模型，对重载列车纵向动力学进行了全面的参数化研究，讨论了空车位置对车钩力的影响，进一步分析了从控机车最佳编组位置［2］。Cole 等提出了一种基于列车纵向动力学、机车牵引控制和车辆系统动力学的仿真方法，可实现纵向、横向和垂向动力学的协同仿真［3］。Sharma 等基于UM 软件建立列车非线性动力学仿真模型，研究了常用制动和紧急制动时车辆间的纵向力特征［4］。Serajian 等基于MATLAB 仿真研究了列车长度（12～52 辆车）对列车系统动力学的影响［5］。常崇义等建立了列车纵向动力学仿真模型，对大秦铁路2 万t 列车车钩力水平进行数值分析，并对模型和求解方法进行验证［6］。刘文涛等通过建立列车纵向动力学仿真模型和基于插值法的空气制动系统模型，研究了列车在长大下坡道循环制动时的车钩力水平［7］。魏伟教授团队将空气制动仿真和纵向动力学仿真深度融合，搭建了TABLDSS 联合仿真系统，可依据列车运行监控记录数据（LKJ）再现列车真实运行过程，也可通过调整车辆和机车各系统参数实现不同编组列车、不同工况的仿真分析，为重载列车安全开行、操纵优化以及空气制动系统的正向设计提供数据支撑［8］，该系统曾在国际权威期刊Vehicle System Dynamics 组织的测评中，获得优异成绩［9］。相较经验公式法或基于试验数据插值法假设空气制动系统各管路、腔室压强变化以及制动波、缓解波传播特性的仿真模型，该联合仿真系统可以真实再现空气制动系统控制阀动作情况和气体流场变化状态，为纵向动力学仿真提供更准确的制动力输入载荷，具有更高的精度，且在空气制动相关仿真计算方面更具优势。

朔黄铁路具有长大下坡道和小半径曲线众多，桥隧相连等特点，其下坡道的最大坡度达到12‰。其中，宁武西—龙宫区段是朔黄铁路驾驶难度最大、操纵最复杂的区段，同时也是制动力判断失误导致停车事件最多的区段，为连续的长大下坡道。目前，朔黄铁路2 万t 列车始发时及进入第一个长大下坡道前要进行试闸，检验列车管是否贯通，并判断制动力强弱，引导后续循环制动操纵策略。在试闸过程中，制动力判断失误会打乱模式化操纵周期，造成列车被迫停车缓风，严重影响运输秩序和运能［10］。统计数据表明，朔黄铁路5 年共计开行2 万t 列车51 029列，其中发生区间停车缓风的17 523列，比例高达34.3%。而停车发生在宁武西—龙宫区段的为8 486列，占发生区间停车列次的48.4%。试闸时制动力判断失误导致列车在循环制动过程中未能在规定地点缓解是停车的主要原因。且目前操纵指导要求根据经验和部分试验结果制订，各种影响因素考虑不周。因此，对朔黄铁路2 万t 重载列车试闸方式与制动力判断标准进行探究势在必行，文中基于TABLDSS 联合仿真系统开展研究。

1 仿真计算模型

1.1 纵向动力学仿真模型

在分析重载列车纵向动力学特性时，重点在于车与车之间的相互作用规律。因此，通常仅考虑每个机车或车辆的纵向自由度，将每辆车视为集中质量，车与车之间通过非线性弹簧阻尼单元相连，单辆车受力如图1 所示。

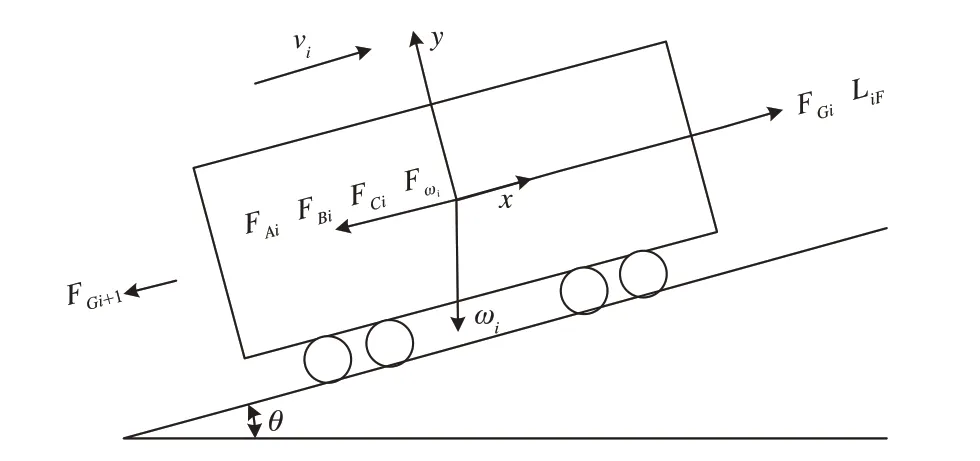
图1 单辆车受力图

依据图1 和牛顿第二定律可列机车车辆运动方程为式（1）～（3），在仿真过程中时刻求解该方程组获得每辆车的状态［11］。该方程组避免了仿真计算时当车辆仅有空气制动力、运行阻力等被动受力的情况下列车向反方向运行。

式中：xi、vi、ωi为第i辆车瞬时位置、速度、重力；、FGi、FL i、FAi、FBi、FCi、分别为第i辆车瞬时惯性力、车钩力、牵引力或电制动力、运行阻力、空气制动力、曲线阻力、坡道阻力。

1.2 列车空气制动系统仿真模型

列车空气制动系统内的气体压强变化既传递制动缓解信号，又是制动力的来源，在对其进行仿真时，需建立机车自动制动机模型、车辆制动系统模型和制动管系模型［12］。其中，制动管系内气体流场变化情况至关重要，也是列车空气制动系统仿真的难点所在，文中所涉及管路气体流动模型基于空气流动理论，假设系统内气体呈一维、有摩擦、不等熵非稳定流动，建立管路内气体流动状态方程组为式（4），由于该方程组无解析解，在仿真模型中采用特征线法求出其数值解。

式中：ρ、u、p、a、k、D、F、f、q、x、t分别为流体密度、流速、压强、声速、比热比、管路直径、管截面积、管内壁摩擦系数、单位时间热交换量、截面位置、时间。

2 现行制动力判断标准及优化思路

2.1 现行试闸方式及制动力判断标准

朔黄铁路2 万t 重载组合列车牵引总重达21 600 t，由2 辆神8 机车和216 辆C80车辆和1 台可控列尾组成，且分别有1 台机车位于列车头部和列车中部，为主控机车和从控机车。朔黄铁路现行操纵指导书要求，一般情况下列车通过宁武西—龙宫区段时需施加3 次制动/缓解（三把闸操纵）；制动力较弱时，施加2 次制动/缓解（二把闸操纵）。现行制动力判断方式：列车在K9+800～K10+000处进行初步试闸，制动初速固定为70 km/h，减压量50 kPa，如若50 s 后列车速度在64 km/h 以上、63～64 km/h 之间、63 km/h 以下时，分别判断制动力为偏弱、适中偏弱、偏强［13-14］。

在列车运行过程中，除在K9+800～K10+000处的初步试闸外，还需在K20+500 处再次进行试闸，制动初速固定为65 km/h，减压量同样为50 kPa，并且施加400 kN 电制动力。根据列车施加空气制动后降速至40 km/h 时所处的位置判断制动力强弱［13-14］，当列车降至该速度时，若列车分别处于K24+300 处之后、K23+800～K24+300、K23+300～k23+800、K23+300 处之前，分别判断为制动力较弱、偏弱、适中、较强。

2.2 现行试闸方式及制动力判断标准缺陷

（1）现行操纵指导书中要求，列车在K14+500处需施加一次空气制动，受该次制动后缓解时的再充风时间不同影响，会导致列车运行至K20+500 处时，列尾压强（列车管压强分布）存在显著差异，即使同样减压50 kPa，列车的制动力也存在差异，进而对制动力的精准判断造成干扰。

（2）不同的列车制动管系漏泄程度不一，同样会使列车试闸前的列车管压强分布产生差异，干扰制动力判断。

（3）K20+500 处的试闸同时也是宁武西—龙宫区段循环制动时的第一把闸，在此处试闸时，司机需要精力高度集中，并在短时间内对列车的制动力进行评估，决定后续操纵模式，对司机的驾驶水平提出了更高的要求。

2.3 列尾压强因素对列车制动力的影响

不同的列车由于其制动管系漏泄程度不一，机车再充风能力不同和前序制动后缓解时的再充风时间不同等因素影响，会导致非首次制动时的列车管压强分布状态产生差异，将直接影响列车再次制动时的制动力强弱以及制动波传播速率等，而列车制动前列车管压强分布状态的重要评价参数就是列尾压强。

在列车真实运行过程中，当其运行至K20+500 处时，其列尾压强并非达到定压，而是多数低于593 kPa。由此，为探究列车管压强分布对制动力的影响，在联合仿真系统中分别将初始时刻列尾压强设置为584 kPa～593 kPa，间隔为1 kPa，从K20+000 处开始仿真计算。

不同初始列尾压强下的列车管压强分布曲线如图2 所示，各工况前108 辆C80的列车管压强差异较小，而后108 辆C80车辆差异显著，且沿列车长度方向的差异逐渐增大。这是由于朔黄铁路2 万t 重载组合列车在缓解时，从控机车前部车辆由主、从机车同时充风，而后部108 辆C80车辆仅由从控机车充风，导致前部车辆列车管压强上升较快，而从控机车后部车辆沿列车长度方向的列车管压强上升速率逐渐降低。

图2 初始时刻各工况下列车管压强分布曲线

仿真计算时，设置列车初始位置位于K20+000处，初始速度为61 km/h，列车在坡道下滑力作用下，速度逐渐上升，待列车到达K20+500处，以65 km/h的制动初速减压50 kPa，列车速度在短暂上升后开始下降，该过程中各工况列车的电制动力施加时机和电制动力值均保证相同。初始列尾压强为584～593 kPa的列车速度变化时域曲线如图3 所示，图中不同初始列尾压强的列车施加空气制动后的速度曲线斜率明显存在差异。

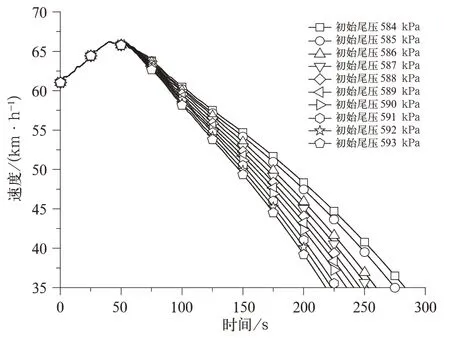
图3 各工况下列车速度变化时域曲线

各工况下的列车空气制动后降速至35 km/h所用时间见表1。由表1 可知，初始列尾压强较低的列车降速所用时长明显高于初始列尾压强较高的列车，初始列尾压强每下降1 kPa，降速所用时长平均增加7.2 s，初始列尾压强584 kPa的列车与初始列尾压强593 kPa的列车相比，降速所用时长增加了34.2%，列车管压强分布不同会对列车空气制动力产生显著影响。

表1 各工况下列车降速所用时长

2.4 试闸方式及制动力判断标准优化思路

列车试闸时应充分考虑线路坡道情况、曲线半径、电制动力大小、车钩力水平以及再充风时间等因素，且试闸时应固定速度、位置、减压量、电制动力大小和施加时机等。现行试闸方式和制动力判断标准中将列车在K20+500 处的试闸作为制动力强弱的主要依据，未考虑列车管压强分布对列车制动性能的影响，而在实际运行中此次试闸由于存在制动管系漏泄情况不同、机车充风性能差异以及前序空气制动后缓解时再充风时间不同等情况，导致试闸时列车管压强分布存在差异，而在上文探究中可知，列车管压强分布存在差异会大幅影响列车空气制动力。

而列车在K9+800～K10+000 处的试闸为始发后的首次制动，制动前其列车管达到定压，此次试闸结果较为准确。其次，由上述探究可知列车管压强分布不同会对列车制动力产生显著影响，由于在列车运行时无法实时监测各车位列车管的压强，但可通过可控列尾实时查询列尾压强，加之列车实际运行中司机判断列车空气制动力强弱需要反应时间，故可将列车在宁武西—龙宫区段第一把闸（K20+500 处制动）前500 m（K20+000 处）的列尾压强作为制动力强弱的判断要素，并结合K9+800～K10+000 处的试闸结果综合判断。

3 试闸方式及制动力判断标准优化

首先对朔黄铁路2 万t 重载列车始发后的首次试闸（K9+800～K10+000 处制动）进行仿真计算，通过调整仿真系统参数来模拟不同制动力的列车，统计各列车施加空气制动后走行至固定位置的降速情况。然后设置试闸列车位于K20+000处，并调整其列尾压强再次进行仿真，在该次仿真中，连续计算列车在通过宁武西—龙宫整个区段时的操纵方式。最后，通过分析总结首次试闸结果以及列车运行至固定位置时的列尾压强并结合列车通过宁武西—龙宫区段的操纵方式得出试闸方式和制动力判断标准。

3.1 试闸方式及制动力判断标准仿真过程

列车始发后的首次试闸，固定地点为K9+800，制动初速70 km/h，减压量50 kPa，电制动力400 kN。由于列车运行至该处时列车管均为充满状态，故在仿真系统中将各工况的列车管压强均设置为达到定压600 kPa。但考虑到列车在实际开行中受C80/C80B混编、装载质量、关门车及天气情况等因素的影响，列车制动能力同样会存在差异，而这种差异由于影响因素较多且存在不确定性，故将其在仿真系统中设置一个用于计算制动系统效率的参数，通过修改该参数来模拟不同制动能力的列车。以列车减压后运行至K10+800 处的速度可以初步判断制动力强弱。K9+800 处的试闸仿真结果见表2，表中从左至右的列车制动力逐渐减弱。

表2 K9+800 处试闸仿真结果

为得到更精准的制动力判断方式，在仿真系统中对首次试闸中的各列车在K20+000 处分别间隔1 kPa 设置其列尾压强为580～593 kPa 进行计算，根据精细化操纵指导要求合理调整列车的操纵方式，且避免追加减压，使列车平稳通过宁武西—龙宫区段，对各工况下列车的操纵方式进行统计分析。各工况下的列车首先尝试采用三把闸操纵方式，第1 把闸制动地点为K20+500 处、制动初速65 km/h，并保证循环制动时的每一把闸均有足够的再充风时间。若采用三把闸操纵方式时列车第2 把闸制动后降速过慢导致无法在长梁山隧道出口（K32+500）前达到缓解要求，而待列车降速至35～40 km/h 可以缓解时，列车在该区段后续操纵中由于再充风时间限制（不低于180 s），已无法完成第3 把闸的制动缓解且可能影响后续制动缓解周期；若列车可以按照精细化操纵指导，要求完成前2 把闸的制动缓解，但在第3 把闸时列车存在降速过慢甚至速度出现上升或超过限速，以及在K43+200 前速度无法降至60 km/h 以下缓解的情况时，列车需要采取追加减压或停车等措施，同样会影响列车后续制动周期，仿真中列车若存在上述情况，该仿真方案中的列车表现为制动力较弱需采取二把闸操纵。宁武西—龙宫区段分别采用二把闸、三把闸操纵方式，每把闸的操纵要点见表3。

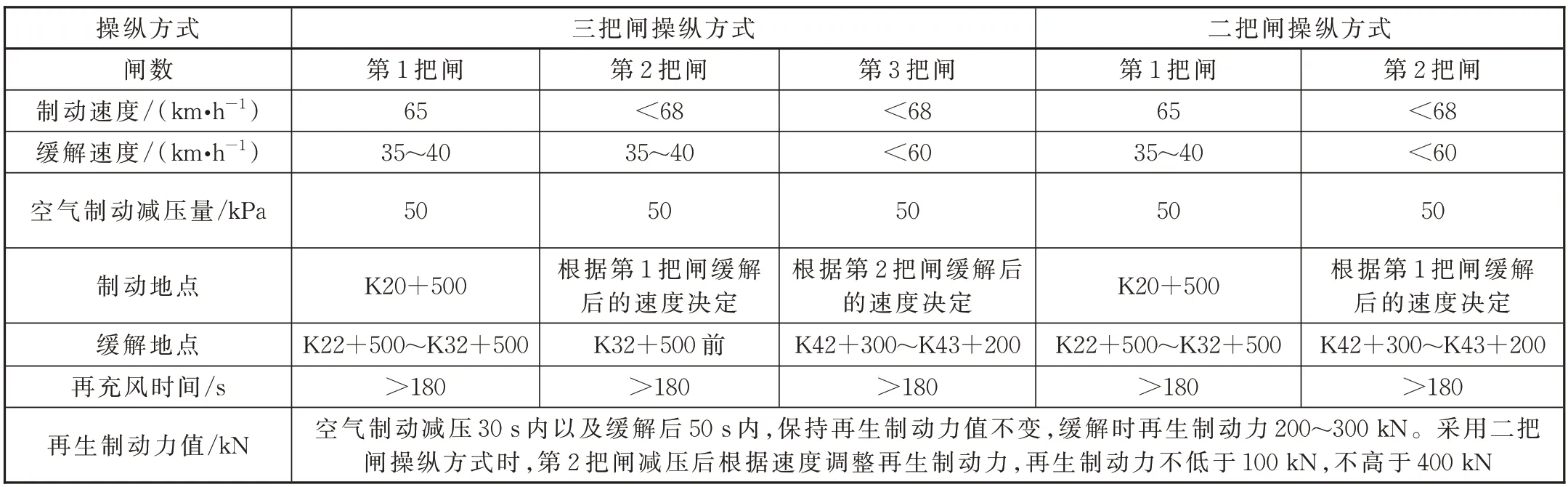
表3 宁武西—龙宫区段2 种操纵方式

由表3 可知二把闸、三把闸操纵方式中的第1把闸操纵要点完全相同，二把闸、三把闸操纵方式的区别在于二把闸操纵方式中的第2 把闸在空气制动后，通过调整再生制动力来控制速度，带闸至龙宫过分相后在K42+300～K43+200 处缓解，而三把闸操纵方式中的第2 把闸在空气制动后待列车速度在K32+500 前下降至35 km/h 时需要缓解，待速度上升后进行第3 把闸的操纵。

在仿真计算中发现，可采用三把闸操纵方式通过宁武西—龙宫区段的列车中，部分工况下的列车也可采用二把闸通过，而多数列车在尝试采用二把闸操纵时由于制动力较强，在第2 把闸操纵时即使将再生制动力降为该区段最低限值（100 kN），列车速度依然下降较快，导致列车在到达K42+300～K43+200 处可以缓解时列车速度较低。若列车在该处以较低速度缓解，待速度上升至65 km/h 可以再次空气制动时，由于再充风时间增加，导致列车在后续的龙宫—北大牛区段制动力增强，速度下降较快，无法实现长波浪制动，而该区段为连续的小半径曲线且为长大下坡道，若列车缓解会产生较大的纵向力，在小半径曲线路况的影响下，纵向力产生的横向分力会使列车存在脱轨风险。部分制动力更强的列车若在宁武西—龙宫区段尝试二把闸操纵时，第2 把闸降速过快甚至发生停车现象。仿真中某工况下列车采用三把闸操纵方式通过宁武西—龙宫区段、采用二把闸操纵无法通过的操作指令及速度曲线如图4所示。

图4 某制动力较强列车采用2 种操纵方式的操纵指令及速度

该仿真方案中的列车在K9+800 处试闸时，到达K10+800 处的速度为62.71 km/h，在K20+000处列尾压强为593 kPa。由图4 可知，该列车可采用三把闸操纵方式平稳通过。而当该工况列车尝试采用二把闸操纵通过该区段时，第1 把闸与三把闸操纵方式的第1 把闸相同，在后续操纵中待第1 把闸缓解后速度上升至65 km/h，空气制动减压50 kPa，50 s 后逐渐降低再生制动力，尝试长时间空气制动，即使将再生制动力降低至100 kN，列车速度依然会下降较快，当列车运行至K39+005 处时列车速度降为0 km/h，无法实现二把闸操纵。

同样，某些工况下的列车采用三把闸操纵方式时存在降速过慢无法在指定位置缓解或超过限速等问题，需采用二把闸操纵方式。仿真中某工况下2 万t 列车尝试采用三把闸操纵无法通过宁武西—龙宫区段，转而采用二把闸操纵，操纵指令及对应的速度曲线如图5 所示。

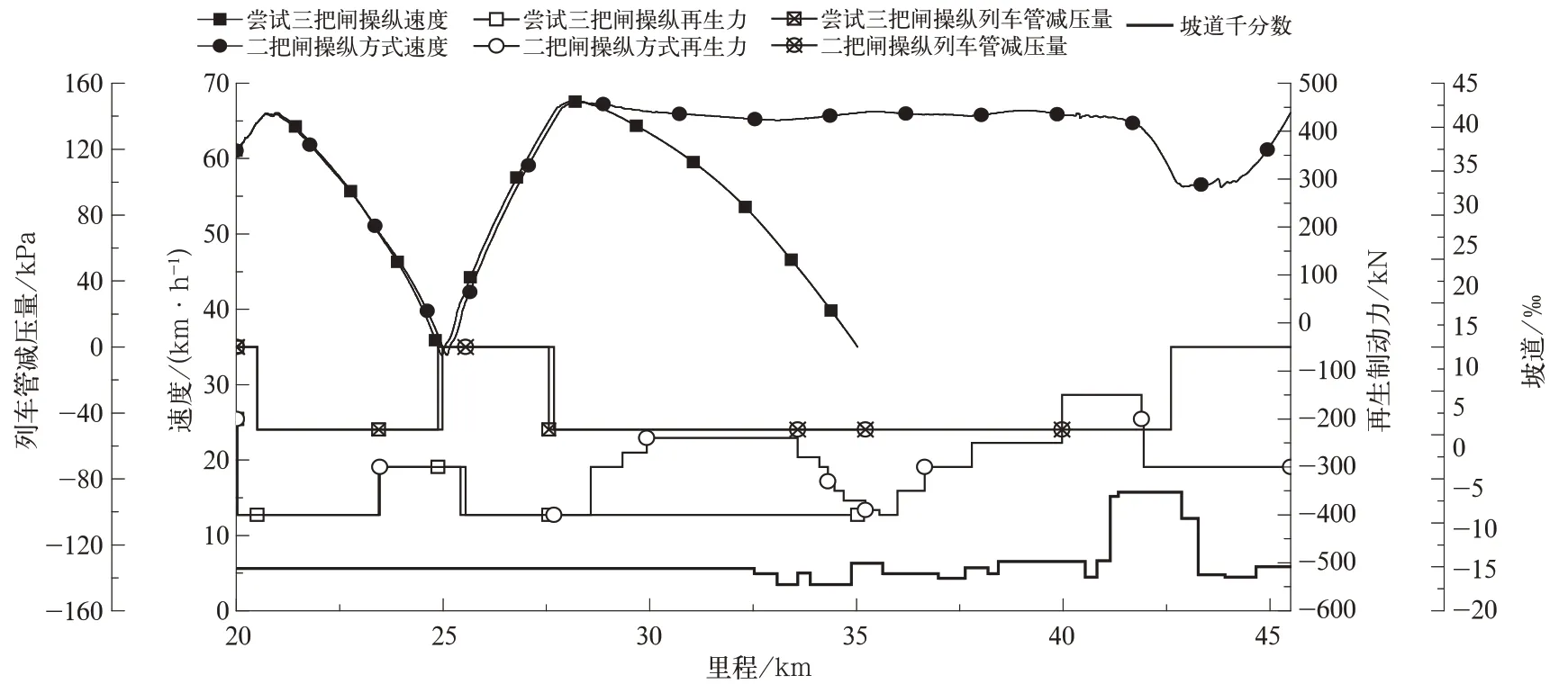
图5 某制动力较弱列车采用2 种操纵方式的操纵指令及速度

在该仿真方案中列车在K9+800 处试闸时，到达K10+800 处的速度为64.07 km/h，在K20+000处列尾压强为580 kPa。由图5 可知，当该列车在宁武西—龙宫区段尝试采用三把闸操纵方式，列车在第2 把闸时，即使将再生制动力调整为400 kN，依然无法在规定位置（K32+500）前下降至缓解速度（35～40 km/h），直至K35+026 处列车速度才降为35 km/h，有违2 万t 列车精细化操纵指导书要求，转而采用二把闸操纵方式。该列车二把闸操纵方式中的第2 把闸在空气制动后，通过调整再生制动力控制列车速度在小范围内波动，实现长时间空气制动，从控机车过龙宫分相后逐渐将再生制动力调整至300 kN，待列车到达K42+605 处时，速度降至58.3 km/h 缓解。

前文所述，部分列车既可采用三把闸也可采用二把闸的操纵方式通过宁武西—龙宫区段，为探究这种情况下采用何种操纵方式更具有优越性，绘出某工况下2 万t 列车同时采用三把闸和二把闸通过宁武西—龙宫区段的方案示例，2 种操纵方式的操纵指令及对应的速度曲线如图6 所示。

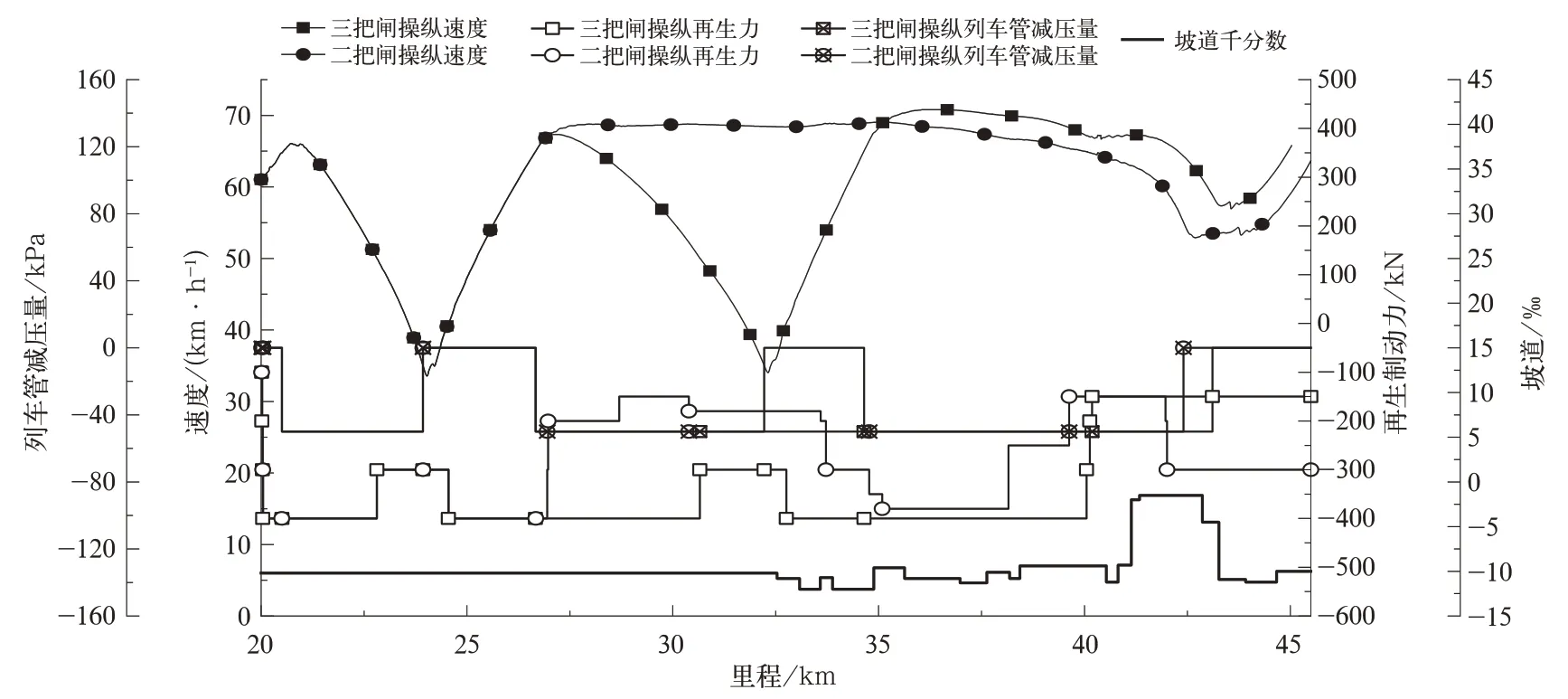
图6 某制动力适中列车采用2 种操纵方式的操纵指令及速度

该仿真方案中的列车在K9+800 处试闸时，到达K10+800 处的速度为63.7 km/h，在K20+000 处列尾压强为585 kPa。图6 中2 种操纵方式的区别在于第2 把闸空气制动后的操纵方式不同。二把闸操纵方式中的第2 把闸在空气制动后，通过降低再生制动力来保证速度不会下降过快，经过长时间带闸至龙宫过分相后在K42+405 处缓解；而三把闸操纵方式中的第2 把闸在空气制动后待列车速度在K32+221 处下降至35 km/h 缓解，缓解后在K34+644 处列车速度上升至65 km/h 后再次空气制动，带闸至龙宫过分相后在K43+107 处缓解。采用二把闸、三把闸操纵方式通过该区段的平均速度分别为60.7 km/h、56.8 km/h，采用二把闸操纵方式的列车平均速度较高，通过该区段的时间较短。该仿真方案的列车分别采用二把闸、三把闸操纵方式通过宁武西—龙宫区段，产生的最大车钩力沿车长分布如图7 所示。

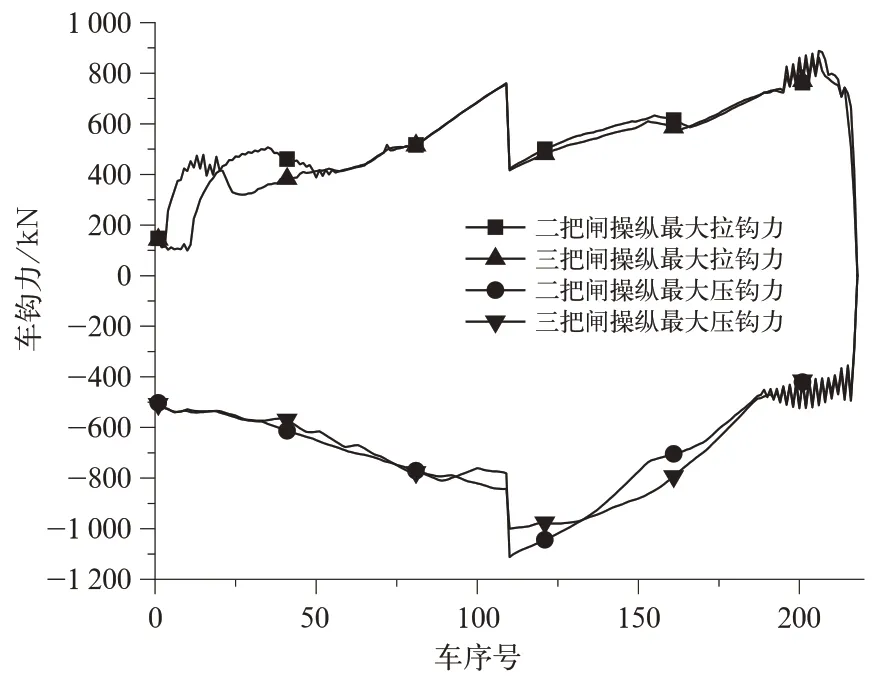
图7 2 种操纵方式下最大车钩力沿车长分布

图7 中车钩力正值为拉钩力，负值为压钩力。由图7 可知，采用2 种操纵方式通过宁武西—龙宫区段产生的最大拉钩力基本一致，而产生的最大压钩力差异也同样较小。2 种操纵方式下产生最大拉钩力的车位均为109 车（从控机车前钩），产生最大压钩力的车位均为110 车（从控机车后钩）。绘制出2 种操纵方式下的109 车、110 车车钩力随里程变化曲线分别如图8、图9 所示。

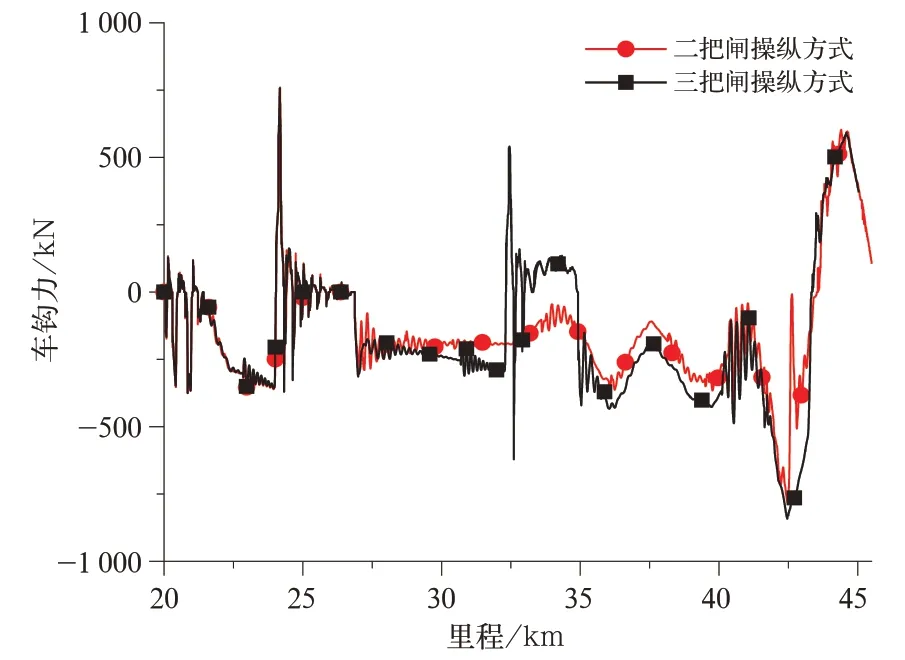
图8 2 种操纵方式下109 车车钩力曲线

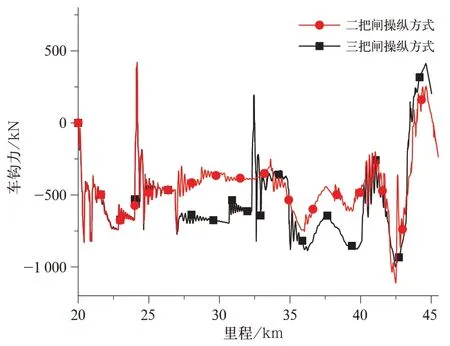
图9 2 种操纵方式下110 车车钩力曲线

由图8、图9 可知，2 种操纵方式的第1 把闸产生的车钩力相同，而区别在于二把闸操纵方式的第2 把闸由于采用调整再生制动力调速，实现长时间带闸的方式，相较三把闸操纵方式减少了一次制动缓解的过程，故而减少了后续操纵中部分因空气制动缓解产生的车钩力，纵向冲动水平较低。此时虽采用三把闸和二把闸操纵方式均可通过宁武西—龙宫区段，但从司机操纵难易的角度出发，采用二把闸操纵可减少1 次制动缓解，有利于司机操纵；从列车纵向冲动水平的角度出发，采用二把闸操纵减少了部分因空气制动缓解产生的车钩力，有利于行车安全；从运输经济性出发，采用二把闸操纵时可提高列车在此区段的平均运行速度，缩短运输所用时间。综合来看，若列车采用三把闸或二把闸操纵方式均可安全通过宁武西—龙宫区段时，采用二把闸的操纵方式较优。

在仿真中若列车可采用三把闸操纵方式安全通过宁武西—龙宫区段，且操纵符合2 万t 列车精细化操纵指导书的要求，制动力判断为较强。若采用二把闸、三把闸操纵均可安全通过宁武西—龙宫区段，列车制动力判断为适中。若列车存在无法在K32+500 前缓解第2 把闸、第3 把闸时降速过慢导致控速困难等情况时，列车需采取二把闸操纵且制动力判断为较弱。

3.2 试闸方式及制动力判断标准优化结果

依据K9+800 处试闸仿真中不同降速情况、K20+000 处不同列尾压强的列车通过宁武西—龙宫区段时的操纵方式，得出优化后的制动力判断标准，如图10 所示。

图10 宁武西—龙宫区段操纵方式仿真结果

综合图10 中列车在K9+800 处试闸，到达K10+800 处的速度（横轴）、列车运行至K20+000处的列尾压强（纵轴）以及列车通过宁武西—龙宫区段时的操纵方式等因素得出列车制动力强弱判断标准。图10中，红色实线为列车制动力强弱分界线；红色实线穿过的方案，制动力适中，列车在通过宁武西—龙宫区段时可采用三把闸或二把闸操纵方式，但采用二把闸操纵方式较优，可降低车钩力水平，简化操纵；位于红色实线左侧和右侧的方案，制动力分别为较强和较弱，在宁武西—龙宫区段分别应采用三把闸和二把闸操纵方式。

4 结论

文中基于TABLDSS 联合仿真系统结合朔黄铁路2 万t 重载列车精细化操纵要求进行仿真计算，提出一种判断列车制动力强弱的方式及判断标准，该方式将列车循环制动前的列尾压强作为判断依据之一。经探究，列车管压强分布不同会对列车空气制动力产生显著影响，该因素在判断制动力时不可忽略，该方法依据列车始发后首次试闸（K9+800 处制动）时，列车运行至K10+800 处的速度以及循环制动前（K20+000 处）的列尾压强综合判断列车制动力强弱。相较依赖司机操纵经验判断制动力的方式，文中的试闸方式和制动力判断标准具有数据支撑，且预留司机反应时间，可有效避免因制动力判断失误造成停车。