基于机器学习的高速列车抗蛇行减振器劣化状态识别方法研究

魏庆，王悦明，吕凯凯，代明睿，杨涛存，杜文然，池长欣

（1 中国铁道科学研究院 研究生部，北京 100081；2 中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081；3 中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081；4 中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081）

抗蛇行减振器作为机车车辆二系悬挂系统的关键部件，对高速动车组运动稳定性至关重要［1］。目前，抗蛇行减振器在一、二级修（运用修）中主要是进行目视外观检查，高级修时需要进行拆解维修或报废处理。若在高级修中的三、四级修时抗蛇行减振器的性能尚能够满足实际的使用要求，过早的拆解检修甚至报废换新无疑增加了运用成本。若能够根据车辆动力学响应数据，与抗蛇行减振器状态参数建立映射关系，进而判断其服役性能状态具有显著的工程应用价值。

为准确模拟抗蛇行减振器的劣化性能及对车辆动力学性能的影响，国内外学者建立了等效参数化模型［2-3］、物理参数化模型［4-5］和非参数化模型［6］3 类减振器理论模型。其中，非参数化模型利用已有的试验数据，采用数学方法建立与测试结果相吻合的数学模型，在模型准确性和计算效率方面具有明显优势。近年来，机器学习越来越多地应用于故障诊断和识别中［7-8］，如邢璐璐［9］使用卡尔曼滤波器实现车辆减振器故障的在线诊断与分离；秦娜［10］提出了基于聚合经验模态分解和5 种信息熵相结合的特征提取方法，识别转向架空气弹簧无气、横向减振器和抗蛇行减振器失效等典型劣化状态；粟丽源［11］采用了一种适用于多通道信号的CNN 模型，用于识别转向架空气弹簧、横向减振器和抗蛇行减振器的失效类型和失效位置。然而上述在研究抗蛇行减振器劣化状态识别时，考虑的多为减振器严重劣化甚至失效等极端工况，设置的劣化工况与实际运用存在一定偏差，脱离了抗蛇行减振器的实际服役性能，在工程应用层面存在诸多不足。

因此，文中选择了符合实际服役状态的劣化抗蛇行减振器，利用非参数化建模方法建立了考虑减振器动态特性的整车联合仿真模型，开展基于机器学习的劣化状态识别研究，研究结论为修程修制优化工作提供理论支撑。

1 抗蛇行减振器建模

1.1 抗蛇行减振器劣化工况设置

结合减振器修程修制优化研究，对运用到限的抗蛇行减振器进行了测试，统计得到的静态阻尼力正偏差为30%，负偏差为15%，节点刚度正偏差为50%，负偏差为20%。通过改变阻尼孔径和橡胶特性，设计了5 种状态的抗蛇行减振器，组合工况见表1。

表1 抗蛇行减振器状态组合工况参数

1.2 抗蛇行减振器动态阻尼特性

传统车辆动力学建模通常采用等效参数化模型，用分段线性描述减振器的阻尼特性，而在台架试验中，减振器的“力—速度”实时曲线在小幅值、高频率的动态工况下近似是滞回曲线，试验频率越高，滞回特性越明显，如图1 所示。减振器“最大力—最大速度”曲线与“力—速度”实时曲线偏差较大，表明分段线性阻尼模型难以体现减振器在小幅值、高频率动态工况下的力学特性。

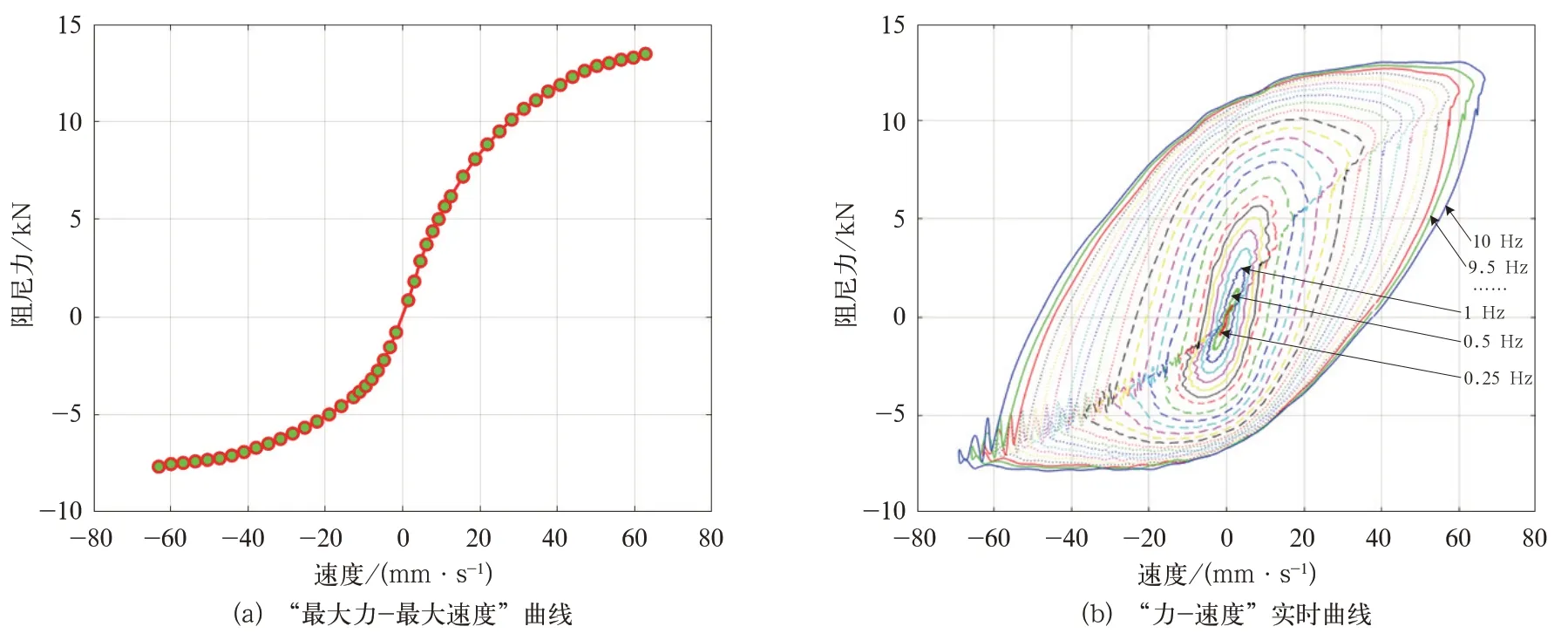
图1 某型抗蛇行减振器台架试验结果（幅值1 mm，频率0.25～10 Hz）

为研究抗蛇行减振器劣化性能变化，首先对表1 所列的5 种状态减振器进行台架试验测试，加载幅值为1 mm 时各减振器的动态频变刚度和阻尼特性如图2 所示。各工况下的抗蛇行减振器动态频变刚度随加载频率的增加呈增加趋势；改变抗蛇行减振器的阻尼也将增加其动态频变刚度；当节点刚度变化±20%时，动态频变刚度值差异不大。抗蛇行减振器频变阻尼随着加载频率的增加呈现先增加后降低的趋势；抗蛇行减振器静态名义阻尼降低15%对其动态阻尼影响不大；当静态阻尼值增加30%时，其动态频变阻尼值均较原抗蛇行减振器有所增加；不同的节点刚度对其动态阻尼也产生一定影响。

图2 5 种状态抗蛇行减振器动态性能试验结果

1.3 抗蛇行减振器非参数化建模

为更好地模拟不同状态减振器对动力学的影响，采用非参数化建模方法，基于测试数据将减振器外部加载的运动参数与输出阻尼力建立映射关系。神经网络模型具有非常强的非线性映射能力，十分适合构建高精度的抗蛇行减振器非参数化模型［12］。BP 神经网络是目前应用最多的一种神经网络形式，具有非线性映射能力、自学习和自适应能力、泛化能力等优点。典型的单隐藏层BP神经网络结构如图3 所示。

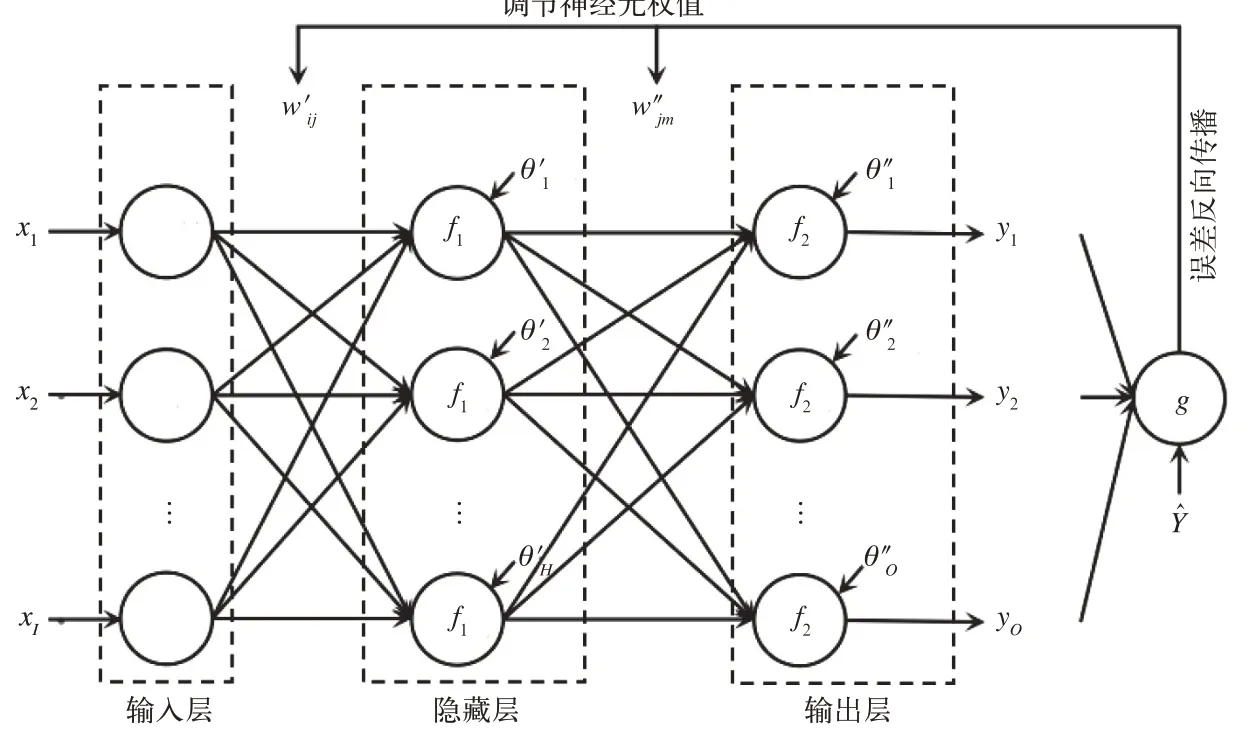
图3 典型单隐藏层BP 神经网络结构

图3中，x1，x2，…，xI为网络的输入值，输入层神经元个数为I；为隐藏层各神经元的阈值，f1为隐藏层的传递函数，隐藏层神经元个数为H；为输出层各神经元的阈值；f2为输出层的传递函数，输出层神经元个数为O；y1，y2，…，yO为网络的输出值；为网络的期望输出；g为误差函数；为输入层第i个节点与隐藏层第j个节点之间的连接权值；为隐藏层第j个节点与输出层第m个节点之间的连接权值。

选取幅值为0.5、1、2、4 mm，加载频率为0.5～12 Hz 动态工况下的台架试验数据作为BP 神经网络模型的训练数据，将抗蛇行减振器位移信号和速度信号作为神经网络模型训练数据的输入，对应的阻尼力信号作为输出，如图4 所示。该神经网络模型的输入层包含2 节点神经元，输出层为阻尼力的单个神经元。根据试验数据量和减振器的复杂程度，隐藏层神经元层数设置为3层，每层设置神经元数量为30 个。

图4 抗蛇行减振器BP 神经网络模型示意图

为验证所建抗蛇行减振器BP 神经网络模型的准确性，各选取一组训练数据内的试验工况和一组训练数据外的试验工况进行仿真计算和验证，训练数据内的试验工况选取幅值为1 mm、频率为0.5～12 Hz，对比结果如图5 所示。对比结果表明，基于BP 神经网络构建的抗蛇行减振器模型的“力—位移”实时曲线和“力—速度”实时曲线与试验结果基本一致，能够体现抗蛇行减振器动态工况下滞回特性和非线性频变特性。

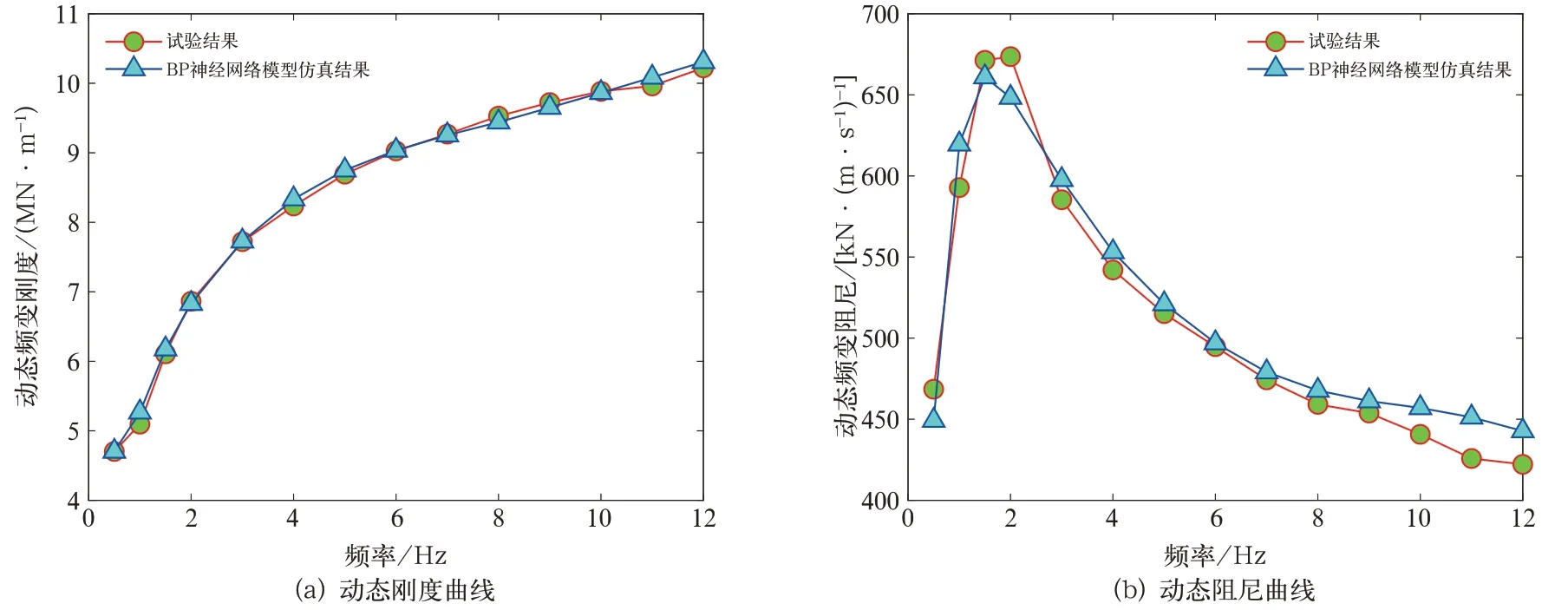
图5 抗蛇行减振器动态刚度和动态阻尼的对比结果

2 整车动力学模型及减振器劣化条件下的动力学响应

2.1 联合仿真模型

建立基于BP 神经网络的抗蛇行减振器非参数化模型与车辆动力学联合仿真模型，如图6 所示。其中，整车动力学模型中考虑了各结构位置关系，以及轮轨接触、各减振器、横向止挡等非线性特性。车体、构架和轮对均具有6 个方向自由度（分别为沿纵向x、横向y、垂向z方向的位移，以及绕其3 个方向的旋转自由度α、β、γ），轴箱仅有绕轮对横向（y方向）的旋转自由度，共计50 个自由度。整车多体动力学模型计算并输出抗蛇行减振器两端的相对位移和相对速度信号；位移和速度信号输入至抗蛇行减振器的BP 神经网络模型中计算动态阻尼力；动态阻尼力返回至多体动力学模型进行动力学计算；重复上述交互计算过程，形成抗蛇行减振器模型与车辆动力学模型的联合仿真。

图6 抗蛇行减振器模型与车辆动力学模型联合数据交互示意图

为验证所建联合仿真模型的准确性，选取了列车以速度350 km/h 通过7 000 m 半径（超高165 mm）曲线工况，对比了试验和仿真结果，如图7所示。模型计算的车体横向振动加速度和构架横向加速度与线路试验结果在幅值和变化规律方面基本一致，验证了仿真模型的准确性。

图7 试验结果与仿真结果对比

2.2 仿真工况设计

根据设置的劣化抗蛇行减振器参数，运用联合仿真模型分别计算了各减振器状态下的列车动力学响应。同时，考虑高速列车服役过程中踏面状态的变化对动力学性能的影响，选取了某型高速动车组车轮标准踏面、轻度磨耗（旋修后运行15万km）和重度磨耗（旋修后运行25 万km）踏面，踏面廓形如图8 所示。

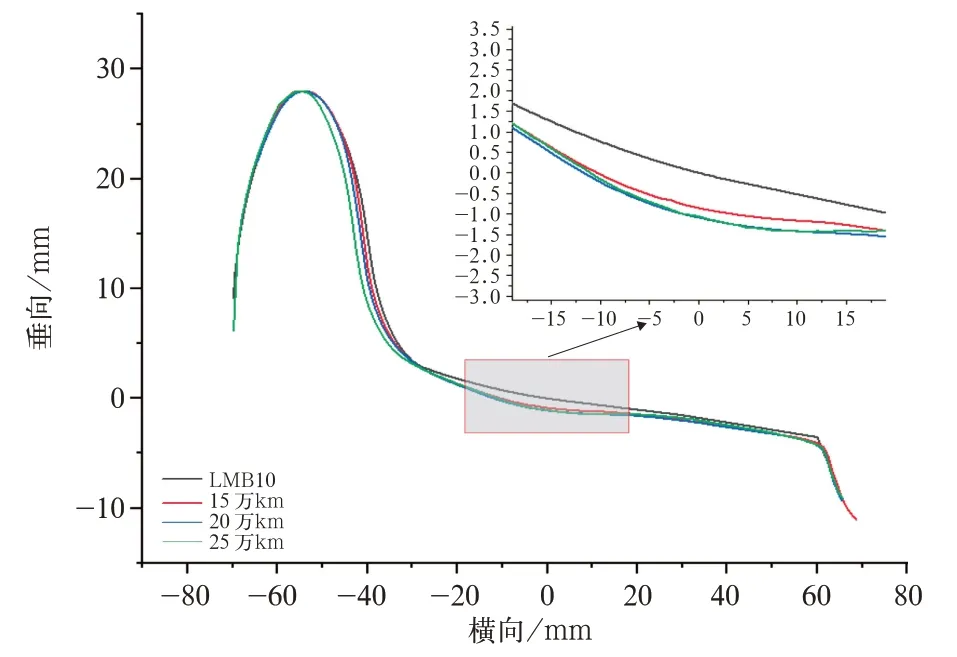
图8 不同程度磨耗踏面廓形图

2.3 抗蛇行减振器劣化对动力学响应的影响

重度磨耗踏面不同状态抗蛇行减振器劣化状态下的车辆动力学响应计算结果如图9 所示。从不同状态抗蛇行减振器条件下的各指标差异来看，构架横向加速度差异较为明显。阻尼130%、节点刚度80%条件下的构架加速度幅值最小，随着节点刚度的增加，构架振动加速度有所增大。当阻尼为85%、节点刚度100%时构架振动加速度幅值最大，与该减振器的动态频变阻尼降低有关。然而，仅依靠构架横向加速度的最大值，难以判断抗蛇行减振器的劣化状态，在某些速度级条件下构架横向加速度甚至呈现出不同的变化规律。结果说明仅通过某几个动力学指标难以直观区分抗蛇行减振器的劣化状态。需要基于抗蛇行减振器劣化状态下的轮轨力、车体振动加速度和构架振动加速度仿真数据，进一步运用机器学习方法开展减振器劣化状态的识别研究。

图9 抗蛇行减振器劣化状态对各动力学指标最大值的影响（重度磨耗踏面）

3 基于支持向量机的抗蛇行减振器劣化状态识别

支持向量机是基于统计学理论和结构风险最小化原理的线性二分类模型，具有较强的泛化能力，同时还具有非线性问题处理能力、对异常点具有鲁棒性等优点，适合对分类问题开展识别［13］。因此，基于SVM 机器学习模型对抗蛇行减振器劣化状态进行识别。

3.1 问题定义和数据处理

将包含5 种状态抗蛇行减振器、3 种踏面状态（标准踏面、轻度磨耗踏面、重度磨耗踏面）的机器学习问题定义为15 种不同组合工况的分类识别问题。

运用计算获取的动力学响应数据，构建各组合工况下的20 通道高速列车转向架关键部件的振动数据集，包含4 位轮对的横向力和垂向力共16个通道，前、后构架横向加速度2 个通道，车体前、后端横向加速度2 个通道。以1 s 为间隔对仿真数据进行切片，计算并提取每个切片内数据的特征值。提取的特征包括时域特征（最大值、最小值、峰值、峰—峰值、均值、方差、均方根值、方根幅值、平均幅值、峰值指标、波形指标、脉冲指标、裕度指标、峭度指标共14 个特征指标）、频域特征（重心频率、均方频率和方差频率共3 个特征指标）、基于聚合经验模式分解（Ensemble Empirical Mode Decomposition，EEMD）的时频特征（选取1～7 阶特征向量的能量矩共7 个特征值），共计24 个特征值。20 个通道数据共计生成24×20=480 维数据特征集。部分典型特征值样本如图10 所示。

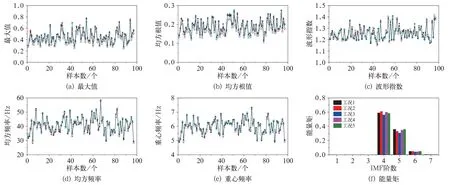
图10 典型特征值样本图

3.2 模型构建和结果分析

选用切分后的70% 数据做训练集，20%的数据做验证集，10%的数据做测试集。同时，为提高机器学习的效率，采用主成分分析（Principle Component Analysis，PCA）将提取的原始特征集进行特征降维。为设置最优的PCA 降维维度，将PCA转化为新样本的维度从1～480 维逐步变化，并利用SVM 进行不同维度下的分类识别，得到在测试集上模型分类的准确度如图11 所示。

图11 SVM 在测试集上分类准确度随PCA 维度的变化趋势

由图11 可以看出，随着PCA 维度的增加，模型的分类准确度也在升高；随着PCA 保留维数越来越高，随着维度的进一步增加，数据中可能引入了冗余或噪声数据，影响了模型的分类性能，使得模型的分类准确度逐渐下降。从识别结果来看，当采用PCA 降维至177 维时，SVM的分类准确度最高，但准确率仅为0.675，识别效果一般。

4 基于卷积神经网络的抗蛇行减振器劣化状态识别

由于设置抗蛇行减振器参数范围内的各动力学响应变化并不明显等原因，导致基于SVM的识别准确度较低。本节进一步研究了基于卷积神经网络的识别方法，15 种不同组合工况分类问题的定义与文中3.1 节保持一致。

CNN 是一种包含卷积运算的多层网络结构，具有良好的特征学习能力，只需构建一个深度神经网络就可以完成特征的提取、降维与分类［14］。典型的卷积神经网络结构如图12 所示。

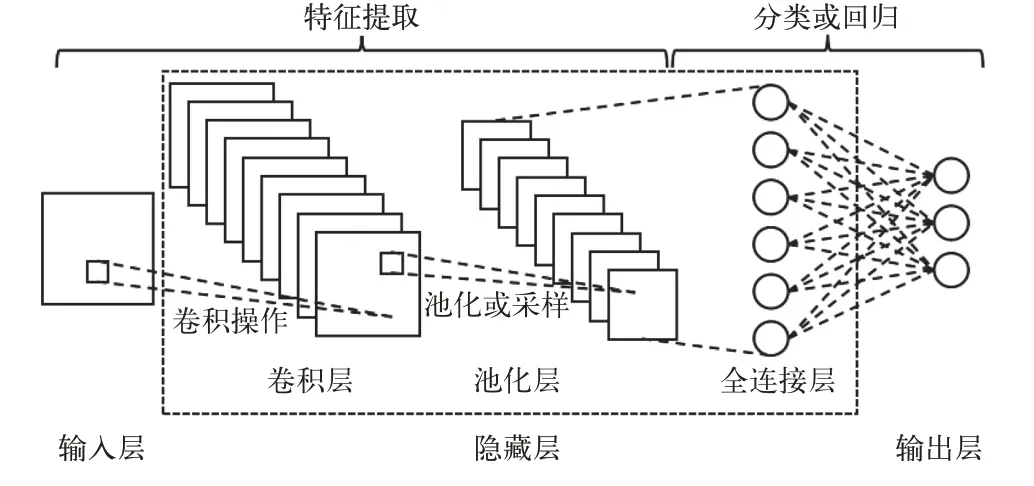
图12 典型卷积神经网络结构

4.1 模型构建及结果分析

用20 个通道的原始数据对建立的模型进行训练，采用滑动窗口的方式对数据进行切分，滑动窗口的长度设为1 000 个数据点。选用切分后的70%数据做训练集，20%的数据做验证集，10%的数据做测试集。将20 个通道振动数据获得的切片直接组合，形成1 000×20的二维矩阵，为利用二维卷积神经网络对数据进行分类建模，对生成的二维矩阵的形状进行重塑，最终形成一个1 000×20×1的三维矩阵作为模型的输入。

建立的CNN 网络模型包括6 个卷积层，其中第1 层卷积层有16 个卷积核，尺寸为128×24，其余卷积层分别有32、32、64、32、16 个卷积核，卷积核尺寸均为3×1。模型设置3 层全连接层，神经元个数分别为128、64、16 个；最后的输出层根据模型自动提取的特征进行劣化状态辨识。为防止模型过拟合，增加模型的泛化能力，模型在最大池化层采用dropout 方法使网络中的神经元以0.2的概率暂时关闭，权重衰减采用L2 正则，正则系数设置为0.003。

训练过程中，模型在训练集和验证集上损失函数的变化曲线如图13 所示。随着迭代次数的增加，损失函数逐渐减小并趋于平稳，达到收敛状态，保留训练过程中验证集损失函数最小的一次作为最优模型参数进行测试。

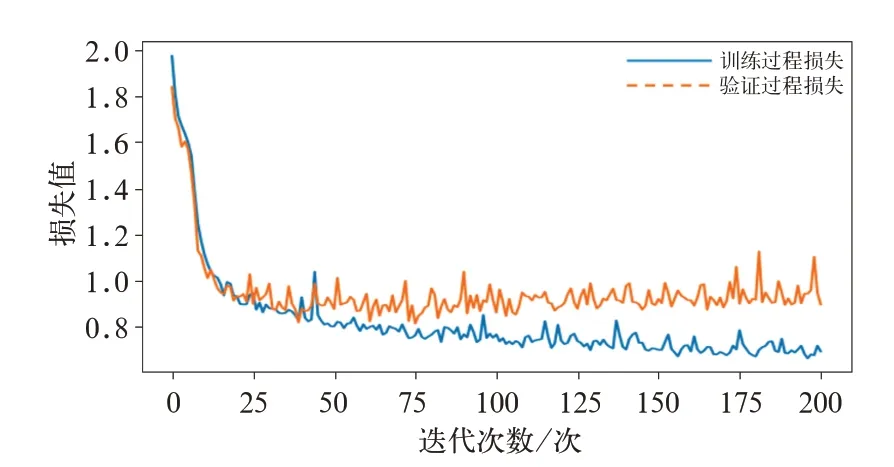
图13 训练集和验证集损失函数变化图

利用训练好的模型对测试集的数据进行识别，将10%的测试数据放到训练好的模型中进行分类，模型在测试集上的分类准确度为0.837。

4.2 问题和通道简化后的模型构建及结果分析

考虑实际运用需求将15 种不同组合工况问题简化，抗蛇行减振器状态简化为原抗蛇行减振器以及劣化抗蛇行减振器2 种状态，分别对应运用中的正常状态和劣化状态。车轮踏面分为标准、轻度磨耗和重度磨耗3 种状态。由此将15 种不同组合工况分类的机器学习问题简化为6 种不同工况的分类识别问题，定义见表2。特征通道由20 个通道精简为4个，即选用2 个车体横向加速度和2 个构架横向加速度测点的振动数据。

表2 6 分类问题定义表

将卷积神经网络模型的第1 层卷积核的大小由原128×20 修改为128×4，最后输出层的神经元个数修改为6，其余参数保持不变，构造出1 000×4×1的输入数据。同样选用切分后的70%数据做训练集，20%的数据做验证集，10%的数据做测试集。训练过程中，模型的损失函数变化曲线如图14 所示。随着迭代次数的增加，损失函数逐渐减小，表明模型的分类能力在逐渐提高。在验证集上，损失函数虽出现波动，但总体趋势逐渐趋于平稳，保留训练过程中验证集损失函数最小的一次作为最优模型参数进行测试。

图14 训练集和验证集损失函数变化图

同样利用训练好的模型对测试集的数据进行识别，模型在10%的测试数据中，分类准确度达到0.879，具有较高的识别精度。

5 结论

文中研究了根据列车动力学响应识别抗蛇行减振器状态，构建了考虑抗蛇行减振器非参数化建模的整车联合仿真模型，基于计算得到的动力学响应数据建立机器学习模型，实现了不同劣化状态的识别。主要结论如下：

（1）结合运用情况设置了阻尼力和节点刚度变化组合的5 种状态抗蛇行减振器，基于BP 神经网络和台架试验数据构建了其非参数化模型，在动态工况下仿真结果与试验结果吻合较好。

（2）建立了抗蛇行减振器非参数化模型与车辆动力学联合仿真模型，计算了不同抗蛇行减振器状态下的车辆动力学响应。结果表明，各动力学指标的变化趋势与抗蛇行减振器状态的关联性不明显，仅通过某几个指标难以直观区分抗蛇行减振器的劣化状态。

（3）将抗蛇行减振器5 种状态和3 种车轮状态定义为15 种不同组合工况的分类机器学习问题。利用仿真得到20 个通道的动力学响应数据构建包含时域、频域和时频域的特征向量集，并利用PCA方法对特征集进行降维，建立基于SVM 机器学习模型进行状态识别，结果表明分类准确度一般。

（4）利用仿真得到的20 个通道的动力学响应数据，构建了基于卷积神经网络算法的机器学习模型，针对15 种不同组合工况的分类机器学习问题的识别准确度达到0.837；考虑实际运用需求，并将15 种不同组合工况的分类简化为6 种不同组合工况的分类问题，通道精简为包含车体和构架横向加速度的4 通道，机器学习模型也获得了较高的识别准确度。

文中通过引入卷积神经网络建立机器学习模型并进行适当的训练和调整，能够有效地对符合实际服役劣化状态的抗蛇行减振器进行识别。识别结果验证了机器学习模型尤其是深度学习模型在类似数据分类任务上的可行性和潜力，为后续针对实测数据开展劣化状态识别提供借鉴。