KdV方程的格子Boltzmann模型求解

陈梦涵,王希胤,李金

(华北理工大学 理学院,河北 唐山 063210)

波动现象是自然界最普遍的现象之一,对于水波的研究也一直是科学和工程研究领域的重要课题。尽管波动问题所涉及的领域不同,但是描述波动现象的方程却是相同的。由于水波千姿百态,用肉眼就可以观察到,因此很早就引起了人们的注意,可以说是人们最为熟悉的一种波。波动是物质运动的重要形式,广泛存在于自然界。波动中被传递的物理量的扰动和振动有多种形式,例如,弦线中的波、空气或固体中的声波、水波、电磁波,等等。为了更加具体地研究各种波动,就产生了各种形式的波动方程,因此,浅水波方程也成为重要的研究对象之一。而Korteweg-de Vries(KdV)方程是1895年由荷兰数学家科特韦格(Korteweg)和德弗里斯(de Vries)在研究浅水中小振幅长波运动时共同发现的一种单向运动浅水波偏微分方程。

在求解偏微分方程地过程中,我们经常用到的数值计算方法有:有限元法(Finite Element Methods),有限差分法(Finite Diference Methods),有限体积法(Finite Volume Methods)和格子Bolzmann(LBM)方法等。其中,有限差分法虽然相对其他三种方法而言简便易行,而且有丰富多样的离散方法,但是它在求解问题时对求解区域的适应性比较差。有限元法虽然采用的网格剖分更加灵活,从一定程度上讲对求解区域具有更强的适应性,但是它在求解间断问题时会受到很大的限制,达不到有限差分法的效果。而有限体积法可以被视为是上述两种方法的结合,虽然能够充分利用有限元网格灵活性和克服差分法对网格适应性差的缺陷,但是数值实验较难进行[1]。作为一种新兴的数值模拟方法,LBM基于Boltzmann方程的离散,是一种自下而上的求解方法。它描述了微观粒子的碰撞和迁移,利用分布函数(一种概率密度分布函数)来确定粒子的分布,即分布函数描述了流体的宏观运动。近年来,由于LBM具有计算简便、良好的并行性、处理不规则的复杂边界容易且对于源项的考虑简单等诸多优势,已经自然而然地发展成为了求解浅水波方程的一种新方法[2]。

在以往的研究中,英国利物浦大学的教授Zhou[3]较为全面地阐述了浅水波方程的LBM理论,包括外力的不同处理格式、湍流模型的构造、多种边界条件的处理方法以及对于许多经典浅水波问题的验证。中山大学环境科学与工程学院的Li和Huang[4]进行了对流-扩散方程与浅水波方程耦合的研究,并采用LB的多松弛模型和双松弛模型分别对流场和污染物场进行了模拟。文献[5]提出了一类粘性浅水方程的晶格Boltzmann (LB)模型,该模型采用源项的二阶矩来恢复控制方程中的粘性,并消除Chapman-Enskog分析过程中产生的附加误差。文献[6]建立了一种适用于浅水方程的晶格玻尔兹曼模型(LABSWE),它用源项如床面坡度,床面摩擦力来求解方程。通过求解定常和非定常流动问题,验证了该模型的有效性。

鉴于以上背景,文章首先给出了格子Boltzmann方法(LBM)的基本理论,然后利用经典的一维五速度(D1Q5)的离散速度模型,给出KdV方程中含有修正项的格子Boltzmann(LB)模型推导公式,最后进行数值模拟,将KdV方程的精确解和模拟解进行比较,然后验证修正模型的精确性。实验结果表明,用格子Boltzmann方法对KdV方程进行求解,其模拟解和精确解吻合度较高。

1 方法

格子玻尔兹曼方法(Lattice Boltzmann Method)是一种基于微观介观的流体力学计算方法,适用于二维或三维流体流动问题的模拟[7]。图1是格子玻尔兹曼方法的流程图:其主要思想是离散化流体的分布函数,通过对分布函数的演化来模拟流体的运动。近年来,LBM由于计算简单、并行性好、易于处理复杂不规则的边界及能简单方便地考虑源项等优势,已经发展成为求解浅水波方程(SWEs)的一种新方法。下面是格子玻尔兹曼方法的求解步骤:

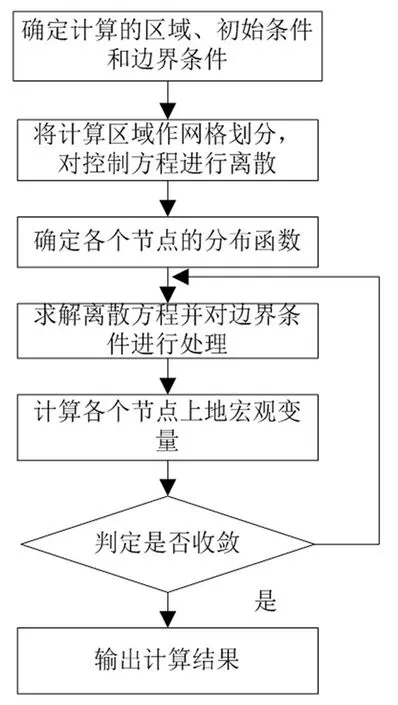
图1 LBM方法流程图

(1)确定格子和速度模型:首先需要确定流场的离散化格点和速度模型。通常情况下,将流体分成若干个小区域,每个小区域都对应一个格点,格点上有一组离散的速度向量。

(2)定义分布函数:为了描述格点上流体的状态,引入一个分布函数g,用来表示在每个格点上,每个速度方向上的粒子数密度。它是时间和位置的函数,通常用离散的速度和离散的时间步长表示。

(3)离散Boltzmann方程:基于Boltzmann方程,对分布函数进行离散化,得到离散化的Boltzmann方程,它描述了分布函数的演化过程。在格子玻尔兹曼方法中,Boltzmann方程可以看成是一个简单的微分方程,其左侧是分布函数的时间导数,右侧是一个碰撞项和一个弛豫项,用于描述粒子之间的相互作用和粒子与流体之间的相互作用。

(4)离散碰撞项和弛豫项:将碰撞项和弛豫项进行离散化,得到离散化的碰撞算子和弛豫算子。碰撞算子用于描述粒子之间的相互作用,而弛豫算子用于描述粒子与流体之间的相互作用。

(5)迭代求解:通过迭代求解离散化的Boltzmann方程,计算出每个格点上的分布函数,从而得到流场的速度场和密度场。

(6)计算宏观量:根据格点上的分布函数,可以计算出宏观量,如速度、密度、压力等。

(7)处理边界条件:对于边界处的格点,需要根据具体的物理问题设置边界条件。

(8)模拟结束:当达到预设的模拟时间或达到收敛条件时,模拟结束。

2 模型简介

2.1 离散速度模型

LBM中一维离散速度模型最常见的是D1Q3模型和D1Q5模型[8],具体如下:

(1)对于D1Q3模型(见图2),模型参数如下:

图2 D1Q3离散速度模型

(1)

其中,ωi为权重系数,c=Δx/Δt为粒子迁移速度,cs是与当地声速相关的量。

(2)对于D1Q5模型(见图3),模型参数如下:

图3 D1Q5离散速度模型

(2)

(3)

其中,ωi为权重系数,c=Δx/Δt为粒子迁移速度,cs是与当地声速相关的量。

2.2 KdV方程

将LB模型应用于KdV方程中,需要将KdV方程离散化成网格上的方程组,然后通过LB模型求解这个方程组。具体来说,LB模型中的速度分布函数被定义为格点上的波高,通过计算速度分布函数在不同时间和空间的演化来模拟KdV方程的行为。与传统的有限差分法和有限元法相比,LB模型具有计算效率高、适合并行计算等优点,因此在模拟非线性波等问题时得到了广泛应用。

考虑非线性偏微分方程一般形式[9]:

(4)

其中,u=u(x,t)是物质在空间x处和时刻t时的密度,α,β,γ,δ为参数。

当β=0,γ=0时,方程(4)化为KdV方程:

(5)

3 模型推导

采用D1Q5模型给出KdV方程含有修正项的LB模型推导,给出 的演化方程为:

(6)

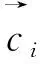
(7)

(8)

其中,λ1,i,λ2,i和pi为调整参数。宏观变量u(x,t)定义为[13-15]:

(9)

为了得到稳定的宏观变量u,假设分布函数gi也处于平衡状态,且有:

(10)

由(10)可得,

(11)

(12)

(13)

使用多尺度分析将方程恢复到宏观方程,引入1个离散的时间尺度和3个连续的时间尺度,其具体表达形式为:

t0,t1=εt,t2=ε2t,t3=ε3t

(14)

对分布函数gi和时间导数进行Chapman-Enskog展开,可得:

(15)

(16)

其中,ε表示任意小的参数,在宏观方程的推导过程中,不妨假设ε=Δt,将(6)式的左边对时间和空间进行泰勒展开,并保留Ο(ε4)项,可得

(17)

将(15)和(16)代入(17)式中得,并对比左右两边可得ε的同阶项:可以得出,

O(ε0)系数:

(18)

O(ε1)系数:

(19)

O(ε2)系数:

(20)

O(ε3)系数:

(21)

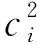
(22)

(23)

同理,结合约束条件(12)和(13),将方程(20)式两边分别乘以ci后并对i求和,得出:

(24)

结合(7)(8)(9)和(19),将方程(16)两边对i求和,得出:

(25)

同理,结合(10)(11)(12)和(22)～(24),将方程(20)两边对i求和,得出:

(26)

将(3.19)×ε+(3.20)×ε2,可得:

(27)

将方程(27)和(4)对比可得:

α=2cτλ1ε,β=(n+1)cτλ2ε

(28)

(29)

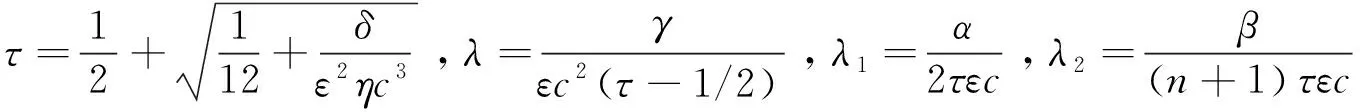
可以得出,方程(27)就是一维KDV方程的LB模型。由方程(7)和(13)式,得出修正函数hi为:

(30)

(31)

4 数值模拟

将LB模型应用于KdV方程中,需要将KdV方程离散化成网格上的方程组,然后通过LB模型求解这个方程组。具体来说,LB模型中的速度分布函数被定义为格点上的波高,通过计算速度分布函数在不同时间和空间的演化来模拟KdV方程的行为。与传统的有限差分法和有限元法相比,LB模型具有计算效率高、适合并行计算等优点,因此在模拟非线性波等问题时得到了广泛应用。

(1)考虑如下的KdV方程:

取c1=2c,c2=c3=1,得出该方程的精确解为:

模拟结果如图4、图5所示。图4和图5分别给出了t=0.01和t=0.25时刻的LB模拟解和解析解的对比图,从图中可以看出:在t=0.25之前,模拟解和解析解吻合的程度较高,但是随之时间的推移,模拟解与解析解存在一定的偏离,这主要是原因有扰动项O(ε4),它在一定程度会对孤子高度、速度以及形状有影响,且当t>0.25时,方程的模拟解和精确解差别较大。

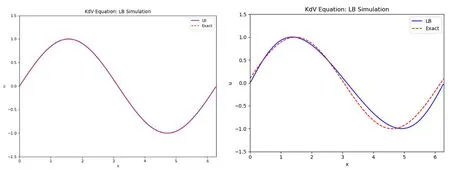
图4 t=0.01,LB模拟解和精确解对比 图5 t=0.25,LB模拟解和精确解对比

(2)考虑如下的KdV方程:

其中,u=u(x,t),u为波动地振幅,x为波横向传播的位移,t为时间。

初始条件为:

u(x,0)=3Asech2(Bx+C),x∈[0,2]

边界条件为:

u(0,t)=u(2,t)=0,t>0

解析解为:

u(x,t)=3Asech2(Bx-Dt+C),x∈[0,2]

设置参数如下:Δx=0.001,Δt=5×10-4,α=1,δ=4.84×10-4,模拟结果如图(6)和图(7)所示.

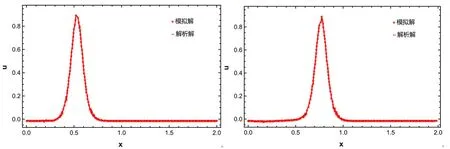
图6 t=0.000 5时,模拟解与解析解对比 图7 t=0.002 0时,模拟解与解析解对比

图6和图7分别给出了t=0.0005和t=0.002时刻的LB模拟解和解析解的对比图,通过对该方程的模拟结果进行分析,发现在t=0.002之前,模拟解和解析解吻合的程度较高,但是随着时间的推移,模拟解与解析解存在一定的偏离,主要的原因是含有扰动项O(ε4),当然也可能是该类波的传播速度极快,长时间模拟就会产生偏差。表1给出了该方程在不同时刻的误差。

表1 方程在不同模拟时刻的误差比较

从表1可以看出,在LB模型下得到的模拟解和解析解非常逼近,无论是L∞误差,还是均方根误差L2和整体相对误差GRE,其两者之间的误差数量级都达到了 ,说明该数值结果是比较理想的。

5 结论

现在,微分方程无处不在,各个科学领域的研究都伴随着微分方程模型。由于实际生活中的微分方程模型形式日趋复杂,为了与实际问题相匹配,微分方程解的形式越来越多样化。本文对两个特殊的KDV方程,利用格子Boltzmann模型求解并与其精确解进行比较,得出使用格子Boltzmann方法对非线性偏微分方程求解取得了较好的效果。在未来的工作中,将尝试继续改进格子Boltzmann模型,并对更加复杂的偏微分方程或者浅水波方程进行模拟。希望本文可以为其他学者在求解偏微分方程方面的研究工作提供一定的参考价值。