XGM2019模型在似大地水准面精化中的应用

丁渃鹏,杨久东,张凌云

(华北理工大学 矿业工程学院,河北 唐山 063210)

引言

将GPS高程测量测得的大地高转换为符合国家高程系统的正常高,其关键在于如何提高高程异常的求解,提高的转换方法通常有使用全球超高阶地球重力场模型,EGM2008是由美国国家地理空间情报局(NGA)EGM(Earth Gravitational Model)团队公开发布的全球重力场模型,该模型的空间分辨率为5′,该模型的阶次完全至2 159(另外球谐系数的阶扩展至2 190)[1]。XGM2019作为EGM2020的实验版,是由慕尼黑技术大学天文和物理大地测量研究所在2019年发布[2],2020年由ICGEM(International Center for Global Gravity Field Models)发布了XGM2019的若干版本,其中XGM2019_2159是与EGM2008相同阶次的全球重力场模型,XGM2019e的阶次完全至5 399(另外球谐系数的阶扩展至5 540),相比于EGM2008,XGM2019e在地面重力数据上提升了包含一个15′的重力异常网格,在陆地上添加了地形信息,在海洋上添加了高程异常数据[3]。

该项研究通过全球重力场模型EGM2008与XGM2019计算出扰动位,根据布隆斯公式计算出不同阶次下的高程异常的长波部分[4],根据实测的GNSS/水准测量数据计算出高程异常值,用于计算对比出2种模型下高程异常的长波部分与GNSS/水准测量计算的高程异常值之间的差距,从而评估XGM2019相较于EGM2008在直接转换为正常高精度上的提升。根据物理大地测量学关于高程异常的相关理论,对EGM2008与XGM2019使用"移去-拟合-恢复"的方法及使用顾及由于地形起伏变化引起的高程异常的短波部分,通过使用二次曲面法对高程异常的残余部分进行拟合,并对2种重力场模型计算的结果进行对比。

1 相关原理

1.1 高程异常

在使用GPS进行定位时,所获得的平面坐标和高程值分别是大地经度,大地纬度和大地高,水准测量获得的高程值为正常高。其中大地高HEH是地面上的点沿法线的方向延伸到参考椭球面上的距离,而正常高HNH是地面上的点沿铅垂线的方向延伸到似大地水准面上的距离。由于我国的高程基准采用1985年国家高程基准,并且高程系统为正常高系统,当已知高程异常时,可以通过式(1)将任一点的大地高转为同一点的正常高。

ζ=HEH-HNH

(1)

1.2 "移去-拟合-恢复"法

根据物理大地测量学理论,高程异常ζ可以通过式(2)进行表达[1]

ζ=ζEGM+ζDEM+ζres

(2)

式中第一项是高程异常的长波部分,是通过全球重力模型计算扰动位,并根据布隆斯公式计算得出;ζDEM是由于地形起伏引起的高程异常的短波部分,用于描述20 km以下的短波特征[5];ζres是残余的高程异常部分,也称为局部似大地水准面中波特征,可以通过重力异常边值问题计算得到。

"移去-拟合-恢复"法的主要思想是将第一项与第二项进行合并,并从已知点的ζ中进行移去,单独剩下ζres,再通过适当的数学拟合方法,对ζres进行拟合,最后在拟合值上加上先前移去的ζEGM与ζDEM,此时就可以得到"移去-拟合-恢复"法后的高程异常值ζ,具体流程可见图 1所示。

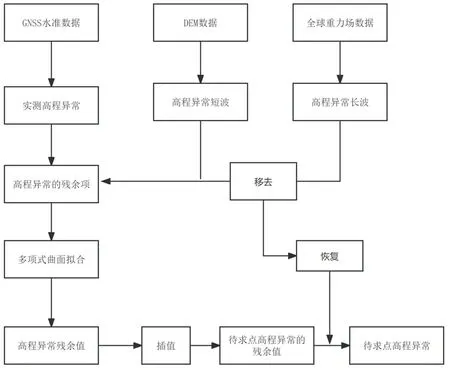
图1 "移去-拟合-恢复"法流程图

1.3 高程异常的长波项

由全球超高阶重力场模型EGM2008,XGM2019_2159和XGM2019e分别计算扰动位,配合布隆斯公式计算出高程异常的长波项,其中EGM2008与XGM2019_2159两者的阶次完全至2 159(另外球谐系数的阶拓展至2 190,次为2 159)[1],而XGM2019e的阶次完全至5 399(另外球谐系数的阶拓展至5540,次为5 399)[3],并且以上模型均可以进行截断。计算高程异常的长波项[1]可参考式(3)。

(3)

1.4 地形改正

由地形起伏变化引起的高程异常变化量δ可以通过式(4)进行表达[6]

(4)

公式(4)中,G为万有引力常数;ρ为地球质量密度;hi为流动单元的高程;h为待求点高程;γ为待求点正常重力;l为待求点到流动单元的距离;dxdy为划分单元的面积。

高程异常短波项 的求解步骤如下:

(1)获取研究区域的DEM数据,目前DEM数据可以通过地理空间数据云中进行下载,目前提供90 m分辨率SRTM数据和30 m分辨率的GDTM数据。

(2)根据研究区域范围划分流动单元。

(3)根据公式(4)计算出每一个格网点由地形起伏变化引起的高程变化量。

(4)根据格网的双线性内插公式计算出待定点高程异常的短波项,计算公式如式(5)[1]。

(5)

公式(5)中δa,δb,δc,δd为流动单元4个格网点由地形起伏变化引起的高程异常变化量,其顺序依次是左下角、左上角、右上角、右下角;l为流动单元的边长;Δx,Δy为待定点到流动单元左下角格网点的坐标差。

2 多项式曲面拟合

2.1 二次曲面拟合

在使用"移去-拟合-恢复"方法中,通过对残余的高程异常进行数学拟合的方法有很多,常用的数学拟合方法有,多项式曲线拟合,多面函数法和多项式曲面拟合,其中二次曲面拟合适用于测区比较平坦的情况,二次曲面拟合方程如式(6)所示:

ζres=a0+a1B+a2L+a3BL+a4B2+a5L2

(6)

公式(6)中ζres为残余的高程异常的拟合值,a0、a1、a2、a3、a4、a5为多项式的拟合系数,通过最小二乘求得,其中要求至少需要6个联测的GNSS/水准点,由模型显著性检验的结果可知,系数只取到二次项[6]。

3 实验分析

3.1 数据介绍

实验数据选取于河南省平顶山市某实习基地,共采集了30个GPS静态数据和其联测的四等水准测量数据,其中大地高的最大值为137.09 m最小值为96.87 m,水准测量的正常高最大值为157.12 m,最小值为116.94 m,具体点位分布如图2和图3所示。其中选取21个点作为"移去-拟合-恢复"当中的拟合点,用于对残余高程异常部分进行拟合,剩余9个点用于检验,利用内、外符合精度来评价建立模型的质量。在顾及地形起伏变化引起的高程异常变化量当中,DEM数据选取的来自地理数据云当中的SRTM90 m分辨率数据,使用流动单元划分为 的格网来求解由于地形起伏变化引起的高程异常变化量。

图2 点位分布图

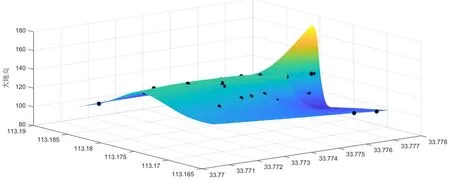
图3 点位地形起伏图

3.2 实验设计与结果

实验一:使用与EGM2008同阶的全球重力场模型XGM2019_2159,利用公式(1)直接计算30个点位的高程异常的长波部分,并与GNSS/水准计算所得的高程异常值做差,从而确定由全球重力场模型计算出的高程异常长波部分与GNSS/水准计算的高程异常之间的差距。计算结果如图 4所示,从图4可看出,在使用XGM2019_2159计算下的残差明显小于EGM2008,其精度有近1倍提升,故在研究区域内使用XGM2019模型下的似大地水准面的符合程度相比于EGM2008更优。

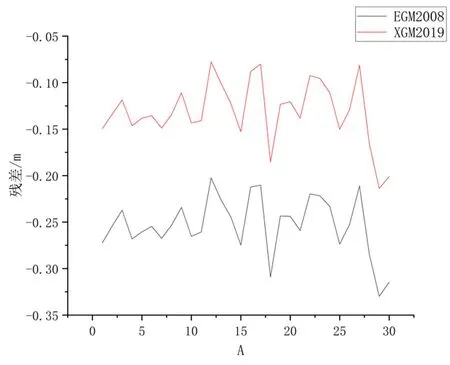
图4 2种高程异常的长波部分与高程异常的残差图

实验二:利用ICGEM提供的不同阶次的XGM2019模型,验证阶次提升的情况下,对高程异常残差值的影响,研究选用EGM2008(阶次为2190),XGM2019_2159(阶次为2190)和XGM2019e(阶次为4 700),并用均方根误差作为评判依据。计算结果如图5所示,当阶次达到4 700时,其均方根误差是明显的优于前两项的,故使用的更高阶次的全球重力场模型进行高程异常长波部分的计算更能提升似大地水准面的精化精度。

图5 全球重力场模型在不同阶数下均方根误差/m

实验三:利用EGM2008,XGM2019_2159,XGM2019e进行"移去-拟合-恢复"法来验证不同模型对似大地水准面精化精度上的提升,选取数据当中21个点作为二次多项式曲面拟合的拟合数据点,采用9个点作为检核点,使用内符合精度与外符合精度来评判建模水平,内符合精度和外符合精度计算公式如式(7)和式(8)所示。

(7)

(8)

式中μ表示内符合精度,v为已知点与拟合点的残差值,n为参与拟合点的个数。RMS表示外符合精度,Δ为已知点与检验点的残差值,m为检核点的个数。内符合精度反映了利用已知点进行建模的模型质量,外符合精度反映了利用所建模型求解检核点的整体质量。利用"移去-拟合-恢复"法计算的内、外符合精度计算结果如表 1所示。

表1 高程异常的残余部分/m

2种全球重力场模型在不同阶次下使用"移去-拟合-恢复"法中内符合精度基本一致,在外符合精度上,XGM2019优于EGM2008和XGM2019e。

实验四:利用EGM2008,XGM2019_2159,XGM2019e进行"移去-拟合-恢复"法在顾及由于地形起伏变化引起的高程异常的短波部分,验证不同模型下似大地水准面精化上的提升,内符合精度与外符合精度的计算结果如表2所示。

表1 顾及地形改正的高程异常的残余部分/m

XGM2019的内符合精度略低于EGM2008与XGM2019e,但是其外符合精度均优于EGM2008与XGM2019e,说明XGM2019的更适合研究区域的似大地水准面的精化工作。

4 结论

(1)GM2020的实验版本XGM2019当其阶次在2 190阶时,相比EGM2008在高程异常长波部分上有厘米级的提升,适用于精度要求不高时将大地高直接转换为正常高使用,表明在研究区域内使用XGM2019下的似大地水准面相比EGM2008在符合程度上更优的结论。但由于XGM2019为实验版本,所以在其他地方的适用性还有待研究。

(2)XGM2019当其阶次在2 190时,其高程异常长波项与高程异常的均方根误差已经达到厘米级,随着重力场模型的阶次不断提高,其精度有厘米级提升,但对于完全规格化缔合函数的选择就更为重要。在ICGEM中提供的完全规格化位系数高达百万行,对于数据预处理也是不小的挑战。

(3)"移去-拟合-恢复"方法中,XGM2019的内外符合精度均优于同阶次的EGM2008模型与4 700阶的XGM2019e模型,但在顾及地形起伏变化的"移去-拟合-恢复"方法中相比未进行顾及地形起伏变化的"移去-拟合-恢复法"在外符合精度上的提升不大。