流体黏性对盐指型双扩散对流扩散通量影响的试验研究

陈 铂,徐孝勤,黄筱云,彭君可,黄剑文

(1.长沙理工大学水利与环境工程学院,湖南 长沙 410114; 2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114; 3.湖南省环境保护河湖污染控制工程技术中心,湖南 长沙 410114)

双扩散对流是一种常见的物理现象,存在于海洋学、大气物理学、地球物理学、生物流体力学以及化学动力学等领域。自然界中,海水受温-盐共同作用产生的大洋环流、软流层在地壳中的运动、大气中热与污染物质的扩散都属于典型的双扩散对流现象。建筑物中热和水蒸气的传导、化学气体的沉积和干燥、晶体成长、金属固化、地下天然气化或人为气化和碳燃烧等工业生产过程也存在复杂的热与物质的双扩散对流[1-6]。

双扩散对流系统的研究始于海洋学问题。20世纪60年代,Stern[7]在研究海洋“盐喷泉”(salt fountain)时发现了双扩散对流现象。双扩散对流是海洋中物质垂直输运的一种重要形式,包括盐指和双扩散阶梯两种情况,当上层是高温高盐水,下层是低温低盐水时,会形成盐指,多发生在热带和副热带海洋的密度跃层;而当上层是低温低盐水,下层是高温高盐水时,容易生成双扩散阶梯,多发生在极地温跃层和受地热影响的海底[8-9]。双扩散盐指现象是由于上层高温高盐的中央水团与其下层来自高纬度冷而淡的水团相互浸入,逐步形成稳定的分层,这种稳定的分层本质是密度分层和温度分层。

Gregg[10]在对盐水入侵的微观结构观测中发现,在上层温热盐水和下层冷淡水的交界面处双扩散对流过程最为活跃,盐指现象也最为明显。马文驹[11]在研究双扩散对流效应引起的异重流时发现,异重流交界面处的物质扩散量比纯分子扩散要大得多,其主要为双扩散盐指效应引起的。Chen等[12-13]在研究瞬时点源羽流在温度分层水体中的运动规律时发现,羽流云团在分层界面会受到阻滞,并在云团底部出现盐指型双扩散对流,造成羽流云团垂向扩散通量和扩散范围的增加。Turner[14]测量了发生盐指现象交界面处的热和盐的垂向通量,并将热和盐的垂向通量同交界面两侧的温度与盐度相关联,证明了盐度垂向通量由于盐指现象的存在而显著增加。Turner[15-16]建议用密度稳定比Rρ来表征双扩散对流强度,并通过室内试验对双扩散阶梯界面的热通量作出推断,确立了双扩散对流热通量公式,即4/3热通量公式。

由于试验水体温度受环境温度影响难以控制,经常使用糖-盐双组分进行双扩散对流试验研究[17],糖-盐双组分系统中,盐的扩散速度是糖的3倍,所以盐溶液对应的是海洋学上的冷淡水,糖溶液对应的是热咸水。Griffiths等[18]对糖-盐双组分系统分层界面的物质通量进行精确测量后发现,糖通量和糖度间呈4/3指数关系。

在早期的试验中,Stern[19]在温-盐双扩散垂直对流试验中利用一系列合理的物理假设得到通量比关系;Howard等[20]在试验中也获得相同的值。由于双扩散对流的特征是盐和热的不均匀垂直输送,所以密度稳定比Rρ和通量比的变化对双扩散对流效率有重要影响。Turner[14]通过热-盐组分双扩散对流试验测得Rρ>2时通量比为0.56;Schmitt等[21-22]在试验中得到通量比的范围为0.4～0.7。这些试验受到了很多质疑,因为测量时,测量装置机械运动产生的扰动会增加额外的通量。Linden[23]使用热和糖进行了常规的分解试验,发现通量比是恒定的0.1,远低于Turner的结果。Turner等[15,24]在进行糖-盐组分双扩散对流试验时,发现Rρ>2时,通量比为0.88～0.94。而Polyakov等[25-26]通过海洋中的观测得出经验公式,得到的双扩散对流热通量与分子热传导公式的计算结果不在一个数量级,其中的原因尚不明确,有待进一步研究。

本文从试验研究入手,结合理论分析,研究糖-盐双组分静态密度分层水体中双扩散对流扩散通量的变化规律,观测盐指型双扩散对流的形成和演化过程,分析流体黏性对盐指型双扩散对流扩散通量的影响,以期进一步了解和掌握盐指型双扩散对流扩散通量变化规律。

1 试验装置和试验方法

以往的研究通常使用冷淡水与热盐水组成的系统,这一系统的组成符合双扩散对流的产生条件：扩散慢的组分形成不稳定梯度,扩散快的组分形成稳定梯度。但是这一系统研究极易受到环境的影响,在试验中热水的热量损失过快,令试验结果产生较大的偏差。

在自然界量化通量较为困难,需要知道哪些因素影响盐指的生长。Turner[14]在试验中发现盐通量和热通量的大小只取决于穿过界面的盐度差和密度稳定比。本文试验选取的糖-盐双扩散系统通过测量试验前后分层流体的组分密度变化,得到双扩散对流扩散通量值。

McDougall等[27]将试验范围扩大到较低的密度稳定比,发现密度稳定比越低,通量越大;当密度稳定比接近1时,净密度通量随着盐指界面黏性和密度梯度乘积的无量纲比值(即Stern数)急剧增加。Schmitt[21]指出,密度稳定比不同净密度通量会发生变化,Stern数通常只适用于密度稳定比较小的盐指界面,Rρ≈2时测得的Stern数接近0.4。

在研究双扩散对流扩散通量时,以往的学者都从密度稳定比入手,发现密度稳定比越接近1,扩散通量越大。本文通过大量试验,发现扩散通量不仅仅是由密度稳定比控制,还和流体黏性有着密不可分的关系。因此,本文在密度稳定比接近1.0(Rρ=1.07)的条件下,改变上下层溶液的黏性,来探究流体黏性对扩散通量的具体影响。

试验采用中部带有活动挡板的矩形水箱,水箱长2450mm、宽1020mm、高4325mm,正常工作水深4150mm,挡板厚10mm,边壁为厚6mm的单层透明玻璃,水箱密闭性良好。水箱中部带有可移动挡板,可以分离上下层流体,从而保证在试验开始前隔绝上下层流体。每次试验开始前控制好实验室的环境温度,根据表1配制试验用糖、盐溶液。试验需要先测量试验流体(清水、盐溶液和糖溶液)的密度、运动黏滞系数、电导率和温度,具体测量步骤如下：

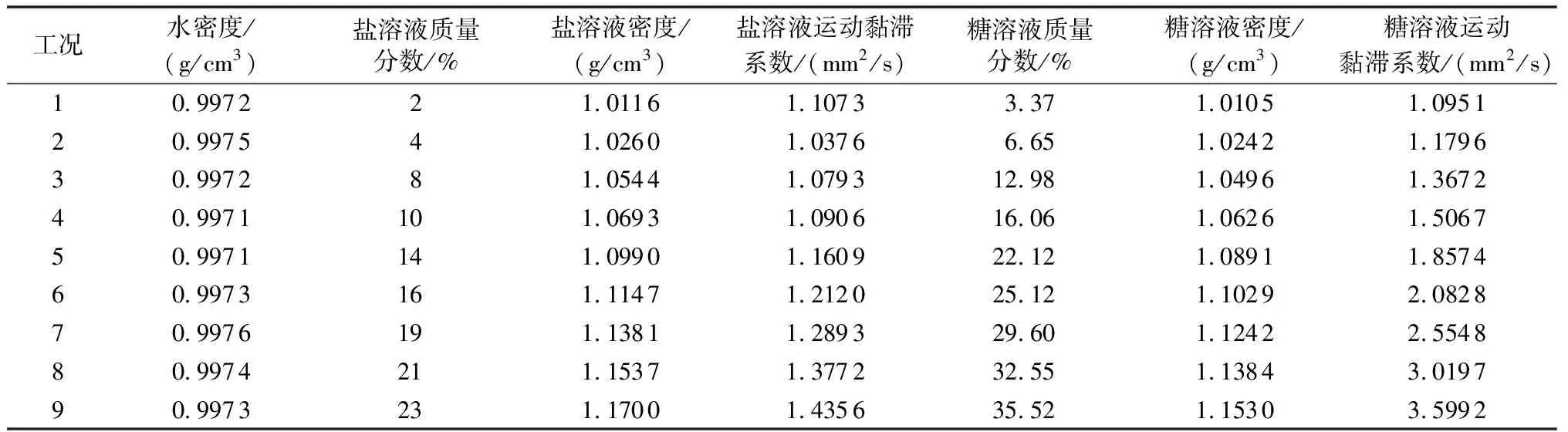
表1 试验工况

a.使用安东帕DMA35型密度计吸取待测溶液,将吸取的待测溶液挤出,重复3次润洗密度计测试管。重复测量待测溶液的密度,直到3个数据两两之间误差小于1%,记录3个数据的平均值以及密度计上显示的待测溶液温度,最后彻底洗净密度计。

b.使用吸球吸取待测溶液,挤入乌氏黏度计中,用吸球将乌氏黏度计中的溶液吸出,重复多次以达到润洗乌氏黏度计的目的。使用润洗后的乌氏黏度计测量待测溶液的运动黏滞系数,若3次结果两两之间误差小于1%,记录3次结果的平均值。然后使用水银温度计测量待测溶液的温度,最后彻底洗净乌氏黏度计。

c.将哈希HQ系列便携式测定仪的电导率探头用清水洗净并擦干,使用电导率探头对待测溶液的电导率进行重复测量,直到电导率值两两之间误差小于1%,取3次数据的平均值作为电导率值,并记录测定仪上显示的待测溶液温度,最后彻底洗净电导率探头。

原溶液各项物理性质测量完成后,开始试验。先打开中间挡板,在下层注入较重的盐溶液,关闭挡板,在上层缓慢注入较轻的糖溶液,注入溶液的同时测量注入溶液的体积。静置2min,调整摄像机直至试验区域全部在取景框内,开始录像并提示试验人员打开挡板并计时,到预定时间后(如10min左右)提示试验人员关闭挡板,挡板完全关闭后结束计时。先使用虹吸管抽取上层溶液,打开挡板后抽取剩余溶液。测量抽取的两部分溶液体积,分别搅拌均匀后测量试验后溶液的密度、电导率和温度,彻底清洗试验水箱。

试验通过电导率这一关键参数推导出试验中糖-盐溶液双扩散对流产生的通量。糖-盐溶液组成的双扩散系统中,在本文试验工况下糖溶液和水的电导率为0.2mS/cm左右,而盐的电导率远远大于糖和水的电导率(150～1000倍)。测量并记录试验前后上下层溶液的电导率,使用试验前的原溶液进行配比并进行分析后即可得到上层溶液进入下层溶液的体积和下层溶液进入上层溶液的体积,具体操作如下：以试验后上层(或下层)溶液的电导率为指标,采用糖、盐原溶液进行组分配制,以获取试验后上层(或下层)溶液中糖、盐原溶液的占比。例如测得工况4试验后下层溶液的电导率为135.3mS/cm,质量分数为16.06%糖原溶液的电导率为0.1942mS/cm,质量分数为10%盐原溶液的电导率为148.8mS/cm。表2为工况4试验后下层溶液的组分配制过程表,开始时在烧杯中加入300mL盐原溶液和30mL糖原溶液,充分混合后得到烧杯中混合溶液的电导率为132mS/cm,小于试验后下层溶液的电导率;继续向烧杯中加入80mL盐原溶液,测得烧杯中混合溶液的电导率为141.6mS/cm,大于试验后下层溶液的电导率;继续向烧杯中加入20mL糖原溶液,测得烧杯中混合溶液的电导率为133.4mS/cm,小于试验后下层溶液的电导率,继续添加少量盐原溶液,依此类推,直至混合溶液的电导率差异小于1%,记录下每次配比加入的糖、盐原溶液体积,进行内插计算,即可得出上层糖溶液进入下层盐溶液的体积,进而计算出扩散通量。

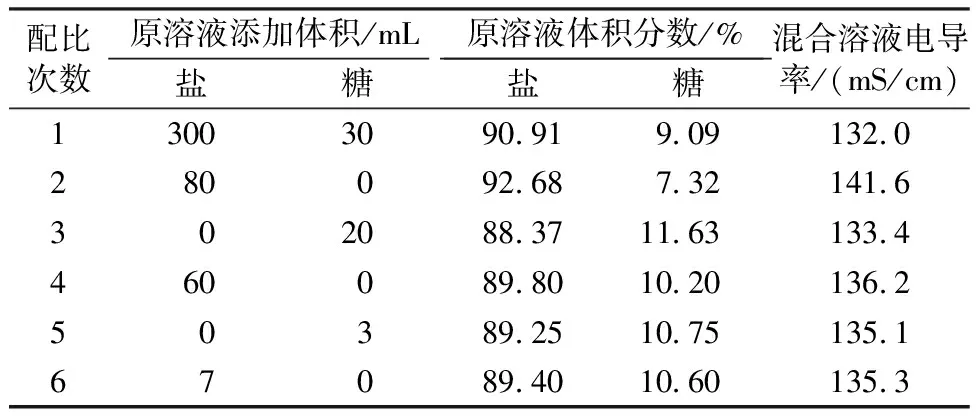
表2 工况4试验后下层溶液组分配比过程

为了明确流体黏性对盐指型双扩散对流扩散通量的具体影响,还需测量因试验水箱中部挡板开启和关闭时扰动产生的扰动通量及分子扩散产生的通量,需要进行清水与盐溶液(水-盐)、清水与糖溶液(水-糖)的对照组试验。将盐溶液注入水箱下层,关闭挡板,将清水注入上层,静置2min;打开挡板(同时开始计时),到预定时间后关闭挡板(同时结束计时),分别抽取上下两层的溶液,并测量溶液的密度、电导率、温度和溶液体积;彻底清洗试验水箱并擦干;将糖溶液注入水箱下层,关闭挡板,将清水注入上层,静置2min;打开挡板(同时开始计时),到预定时间后关闭挡板(同时结束计时),分别抽取上下两层的溶液,并测量溶液的密度、电导率、温度和溶液体积,最后彻底清洗试验水箱。

2 试验结果与分析

糖-盐双组分试验取密度稳定比为1.07,图1为拍摄到的糖-盐分层界面盐指现象,可以明显观察到上下两层分层界面处有手指状的图案相互扩散的现象。由于盐的扩散速率远快于糖的扩散速率,所以当上层液体的某一流体团有一微小的流体团向下运动时,该流体团即与所到达处的盐度相平衡,使该流团密度变得更大,促使其向下运动。另一方面,下部的某一流团有一微小的向上运动,则新位置处糖度较高,流体膨胀密度更小,促使其向上运动。这种局部上下运动形成盐指现象。穿过分层界面的组分溶液体积除了有双扩散对流扩散通量Q3外,还有开合挡板扰动产生的通量Q1和分子扩散产生的通量Q2,每次开合挡板要求轻缓,时间控制在40s左右,故将扰动产生的通量视为瞬态值,与试验时间无关。定义通过分层界面组分溶液体积为V=Q1+Q2t+Q3t,其中t为试验时间,Q1、Q3的大小和溶液黏性相关。

图1 试验中的盐指现象

使用糖溶液和盐溶液分别与清水进行对照组试验,对照组试验中仅有一种组分,不会出现双扩散对流。图2为对照组试验单组分溶液扩散入清水中的体积分数与Atwood数(A=(ρ1-ρ2)/(ρ1+ρ2),其中ρ1为下层溶液密度,ρ2为上层溶液密度)的关系图。对照组试验中仅存在扰动通量Q1和分子扩散通量Q2,其通量与双扩散对流试验的Atwood数成反比,由于不同试验组的密度稳定比相同,这就意味着Atwood数越大,糖、盐溶液的浓度越大,它们的黏性也越大。而糖、盐溶液试验中,下层糖、盐溶液的黏性越大,推拉挡板所产生的扰动影响也理应变小。由图2可知,糖、盐溶液的扰动扩散通量与流体黏性呈负相关关系,由此可以假定扰动扩散产生的通量和运动黏滞系数的关系为Q1=c1/ν,其中c1为常系数,ν为运动黏滞系数。

图2 对照组试验跨界面扩散溶液体积分数与Atwood数关系

根据菲克定律[28],分子扩散通量的关系式为Q2=-DdC/dz,其中C为浓度,z为垂向位置,负号意味着高浓度向低浓度扩散,D为分子扩散系数。本试验上下两层溶液均匀,中间挡板厚度1cm,挡板扰动会产生一个1cm的薄层,其内部浓度梯度为dC/dz,即上下两均匀层浓度除以薄层厚度。

根据麦克斯韦-玻尔兹曼分布,认为流体中流体分子运动驱动内部溶质分子扩散,可以假定分子扩散系数与流体温度T遵循以下关系：

(1)

液体温度越高,扩散速度就越快。由此,可以假设在水-糖、水-盐试验中扰动扩散和分子扩散产生穿过分层界面组分溶液的总体积为

(2)

式中c2为常系数;t为试验时间。通过二元回归分析可得系数c1、c2的值,且决定系数R2较大,说明结果较好,具体数值见表3。

表3 拟合结果

为了验证扰动扩散通量和分子扩散通量在跨界面扩散溶液体积中的比重及方程的可行性,将试验数据代入式(2),式中c1、c2取拟合结果值,得到单组分对照组试验跨界面扩散溶液体积值,如图3所示。在水-糖、水-盐溶液中,分子扩散通量和扰动扩散通量各占一定比例,扰动扩散通量随着黏性的增大而减小,试验用时较少时,扰动扩散通量比分子扩散通量大很多。糖溶液分子扩散通量比盐溶液分子扩散通量大一些,这是浓度梯度不同引起的差异,浓度梯度越大,分子扩散通量越大。

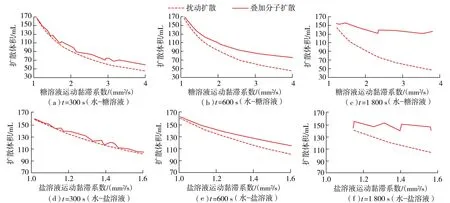
图3 对照组试验扰动和分子扩散体积对比

在糖-盐双层系统中,盐的分子扩散率是糖的3倍,两种扩散率不同的流体会引起双扩散对流,而双扩散对流又会产生扩散通量。因此,糖-盐双层系统试验与水-糖、水-盐分层试验相比多了一项双扩散对流扩散通量。根据对照组试验数据可知糖溶液和盐溶液的扰动扩散体积和分子扩散体积。通过试验,测得了糖-盐双层系统的总扩散体积,用总扩散体积减去预测的扰动扩散体积和分子扩散体积并除以分层界面面积和试验时间,可以得到糖、盐溶液的双扩散对流扩散通量,其结果如图4所示。在相同密度稳定比下,流体黏性越大,糖、盐组分产生的双扩散对流扩散通量整体呈减小趋势。

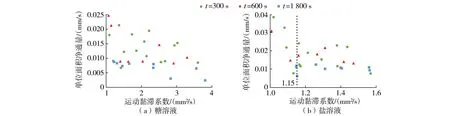
图4 糖、盐溶液运动黏滞系数与双扩散对流扩散通量关系

图5为每次试验中糖、盐溶液的运动黏滞系数关系,每组工况糖溶液与盐溶液的运动黏滞系数都在逐渐增大。而在糖溶液的运动黏滞系数大于1.15mm2/s后,糖溶液的运动黏滞系数迅速增大,此时,糖溶液的运动黏滞系数增长速率远大于盐溶液的运动黏滞系数增长速率。在图4(a)中糖溶液运动黏滞系数增大的同时,糖溶液的扩散通量在逐渐减小;在图4(b)中盐溶液的运动黏滞系数在1～1.15mm2/s之间时,盐溶液的扩散通量规律与糖溶液相似,随着盐溶液运动黏滞系数的增大而减小。当试验流体的运动黏滞系数都大于1.15mm2/s时,盐溶液的运动黏滞系数增长速率比糖溶液的运动黏滞系数增长速率慢很多,此时盐溶液的扩散通量基本不发生变化。

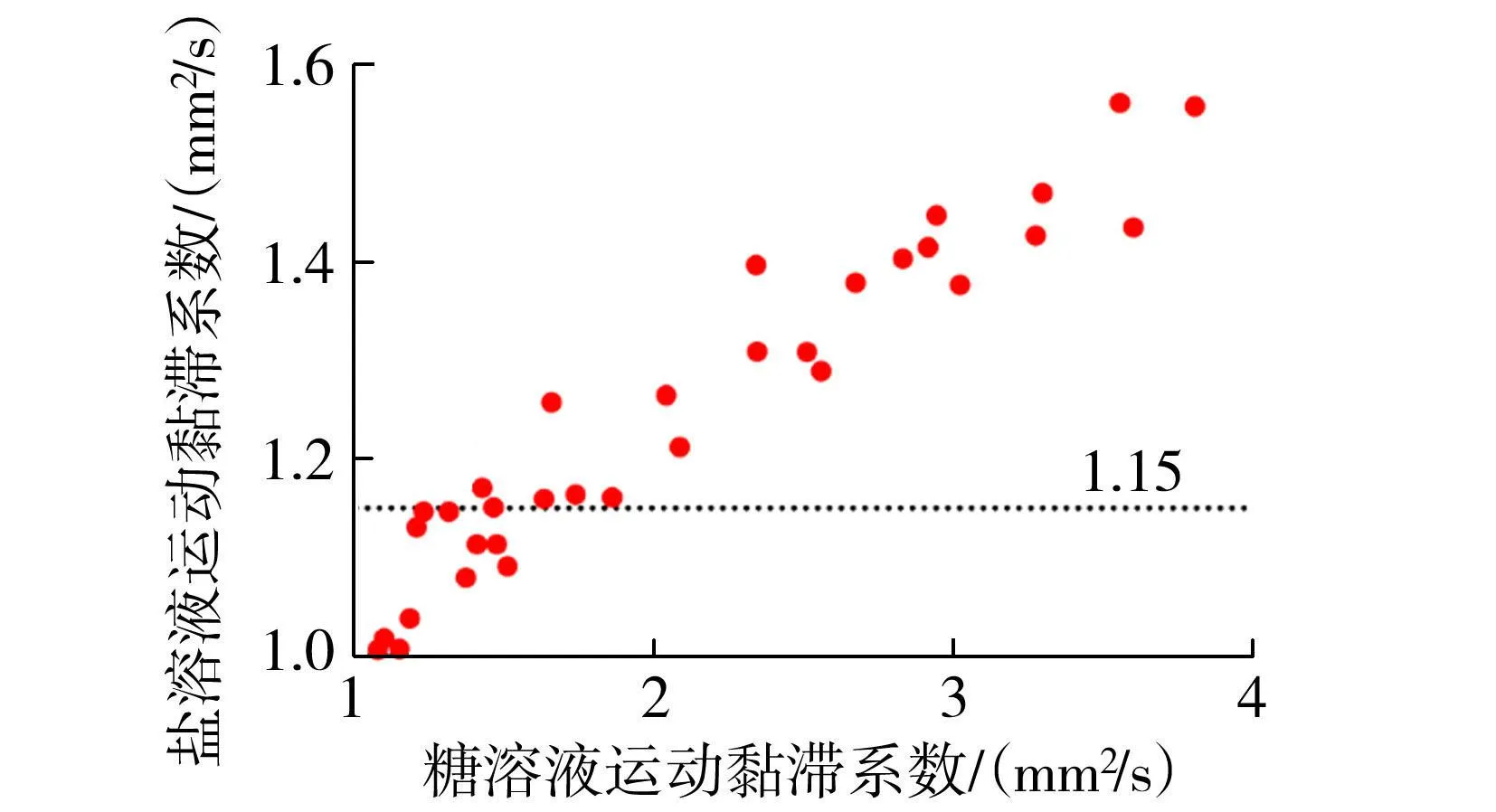
图5 各工况糖、盐溶液运动黏滞系数关系

前人对影响盐指型双扩散对流扩散通量的因素做了许多研究,Stern提出当流体黏性和密度梯度乘积的无量纲比值Stern数趋近于0(分子是分母的高阶无穷小),盐指的线性增长就会停止[29]。对于密度稳定比较大时(Rρ>2),盐指不稳定性影响有限,对物质的垂直输运没有显著影响。Stern数通常只适用于低密度稳定比的盐指交界面,本文试验的密度稳定比较低,且Stern数的分子和分母在一个数量级,盐指的生长及扩散不会停止和失稳。在盐指交界面可对Stern数进行计算分析,图6展示了Rρ=1.07时,Stern数与流体黏性的关系,可见Stern数与流体黏性呈负相关关系。

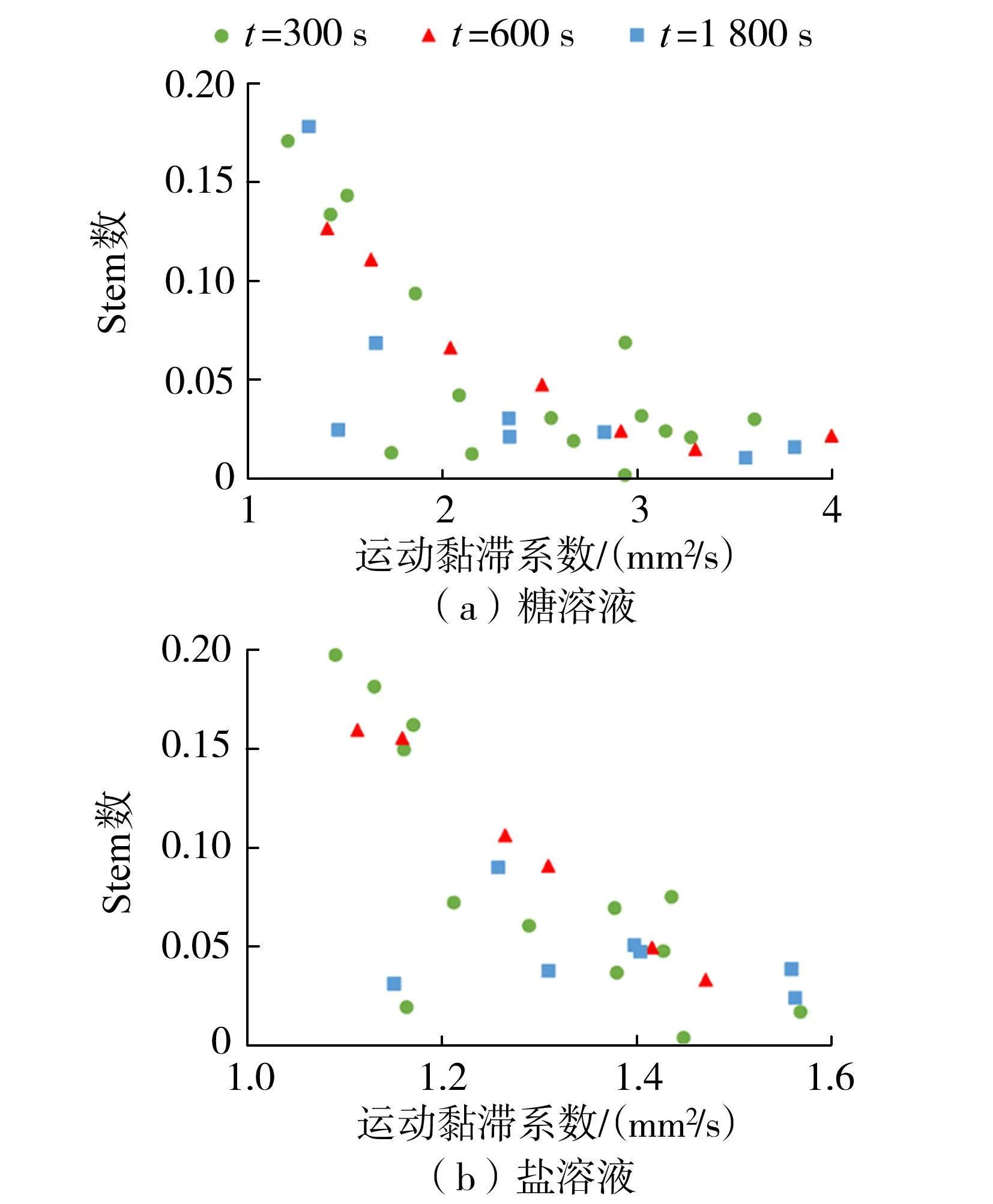
图6 Stern数与流体运动黏滞系数关系

3 结 论

a.流体黏性对盐指型双扩散对流扩散通量的影响不可忽略,在双扩散对流强度相同的条件下,试验流体黏性越大,盐指型双扩散对流扩散通量越小。

b.糖-盐双层系统中,试验流体的黏性均较小时(运动黏滞系数小于1.15mm2/s),糖和盐这两种组分跨界面的双扩散对流扩散通量随流体黏性增大而减小的趋势相近;当两种组分的质量分数持续增加时,盐溶液的黏性仍缓慢增加,而糖溶液的黏性迅速增大,此时糖组分的跨界面双扩散对流扩散通量仍会随糖溶液黏性增大而减小,但盐组分的跨界面双扩散对流扩散通量不再变化。

c.试验中糖-盐双层系统的密度稳定比接近1,为Rρ=1.07,此时观测到Stern数与流体黏性呈负相关关系。