生物附着现象对有压输水工程过流能力的影响

张建建,张社荣,刘 涵,2,王 超,王枭华,姜佩奇,3,崔 溦

(1.天津大学水利工程仿真与安全国家重点实验室,天津 300350; 2.中国电建集团昆明勘测设计研究院有限公司,云南 昆明 650051; 3.水利水电规划设计总院,北京 100120)

随着长距离引水工程运行年限的增长,工程运行过程中的新问题如淡水壳菜等生物污损现象不断凸显。调研发现,在某输水结构壁面上以淡水壳菜为主的污损生物最大附着厚度达15mm,侧壁单位面积最大密度近7万个,致使混凝土发生大面积霉变和表观缺陷。附着在输水建筑物表面的生物会增加壁面粗糙度,从而导致壁面阻力增加,引发流态改变、过流能力减小以及运行水位超限等一系列问题[1-3]。输水建筑物在淡水壳菜繁殖条件下的糙率可从0.0164增长至0.0180,造成沿程水头损失增大[4-5]。这些问题已成为制约工程长期运行安全、加剧潜在工程运行安全风险的关键要素。

针对上述问题,已有学者对生物附着现象对水流水力特性的影响进行大量研究。 Dong等[6]通过多孔介质模拟贻贝串模型,用雷诺平均的纳维斯托克斯(RANS)方程来模拟贻贝场周围的流场,综合分析贻贝的密度和斜流之间的关系,并对贻贝串在不同水深下的水动力特性进行了数值研究分析。Constantinescu等[7]利用试验和数值技术分析了固定在平板通道上的潜贻贝群周围的床层摩擦速度分布。O’donncha等[8]分析了有贻贝类生物附着的养殖棚和潮汐能装置对流体动力学的影响。Lin等[9]观察了悬浮贻贝养殖场对潮流的水动力影响,表明悬浮贻贝串引起的表面摩擦远大于海床摩擦。Kervella等[10]在试验和数值模拟的基础上,描述了河道牡蛎群周围整体水流结构周围边界层的不对称发展。Andrewartha等[11]对生物附着的明渠进行阻力测量和近距离摄影测量表面特征研究,发现生物表面的有效粗糙度大于物理粗糙度。张海玲等[12]对粗糙壁面的明渠进行试验研究,结果表明明渠壁面结构特征造成了水流阻力组成成分改变。槐文信等[13-15]以淹没柔性植被为粗糙因素对淹没柔性植被覆盖的明渠进行研究,得出植被上部水流的纵向流速分布符合对数律的结论。

本文针对我国输水工程中生物污损现象造成的壁面混凝土剥落、有效过水断面缩小以及水质恶化等问题,依托南水北调中线某输水建筑物开展室内模型试验,并采用多孔介质域数值仿真淡水壳菜附着对有压输水工程过流能力的影响。

1 物理模型仿真原理

1.1 室内模型及加糙方法

室内模型采用内径为600mm的预制管拼装,管道总长14m。前池、后池均采用钢板制作,尺寸为3m×3m×1.5m,每根管道进口安装矩形闸门;前池与后池之间设置1根回流管,直径为200mm[16],如图1所示。

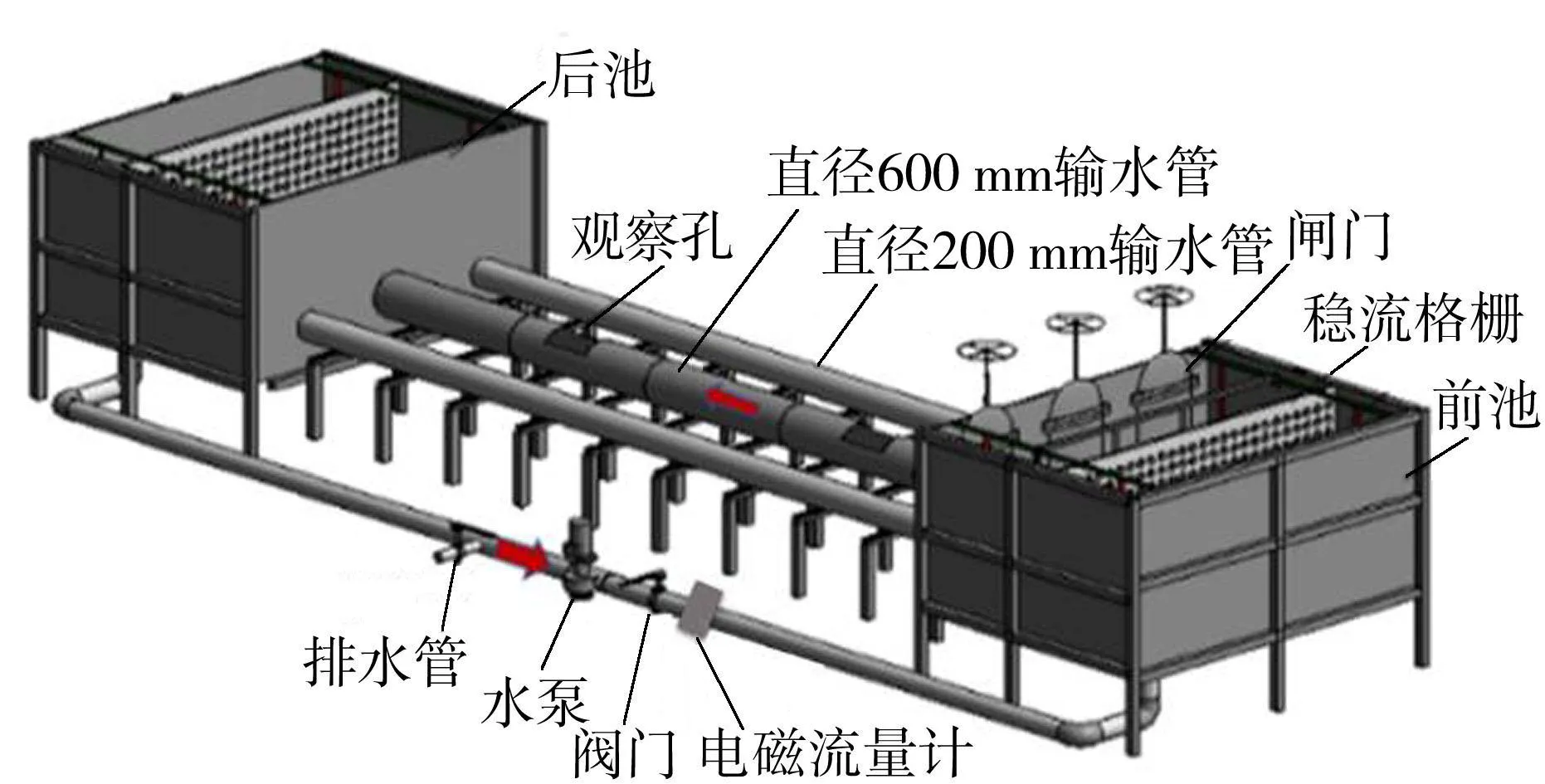
图1 室内模型结构

根据前期调研结果,在有压输水工程中淡水壳菜在内壁四周均有分布,并且沿程分布较为均匀。为真实模拟淡水壳菜附着于建筑物的特性,试验选用淡水壳菜壳体分散粘于管道内壁上,模型各部位均匀粘贴。根据淡水壳菜附着正投影面积与输水建筑物壁面的比值(面积占比)表征室内模型中淡水壳菜附着密度[17],设置模型内壁附着面积占比分别为4.8%、5.8%、6.0%。

1.2 多孔介质域

根据已有研究[6,13],采用多孔介质域模拟建筑物壁面生物附着层对水流的扰动效应,多孔介质模拟方法是将流动区域中固体结构的作用看作是附加在流体上的分布阻力,在动量方程中新增源项来表明多孔介质的阻力作用,源项方程为

(1)

式中：Si为第i(x,y,z)方向的动量方程源项;vj为流速;Dij为黏性损失项;Cij为惯性损失项;μ为动力黏滞系数;ρ为流体密度。

对于各向同性多孔介质,式(1)可简化为

(2)

C2=3.5(1-ε)/Dpε3

式中：D1为黏性损失系数;C2为惯性损失系数;ε为孔隙率;Dp为颗粒平均直径。

制作淡水壳菜实体并采用排水体积法确定不同附着密度的孔隙率[18],各参数计算结果见表1。

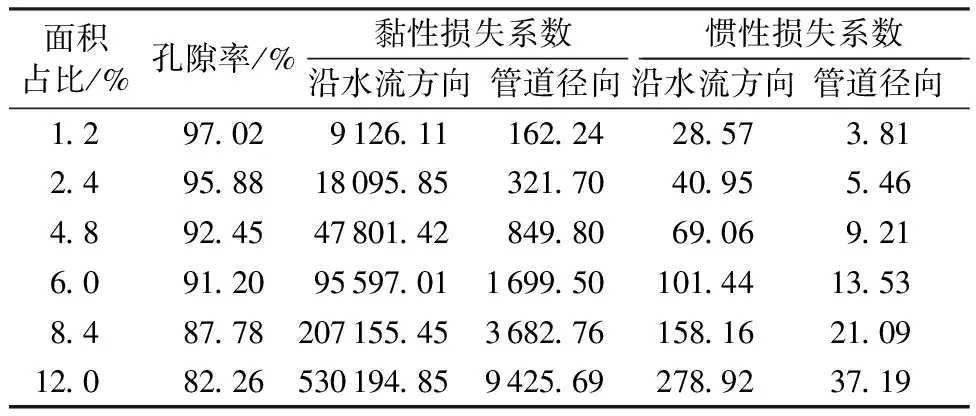
表1 多孔介质域参数

1.3 计算域及工况设置

本文采用HYPERMESH软件来生成结构化网格,在保证网格质量的同时减少整体网格单元数目。根据现场调研结果建立不同附着面积占比的多孔介质域,设置长度为12m。淡水壳附着区段生成网格单元为463276个,网格节点为530432个;其他区域网格单元为1899726个,网格节点为1912242个。进口设置为速度入口,出口设置为压力出口,三维流体模型见图2。

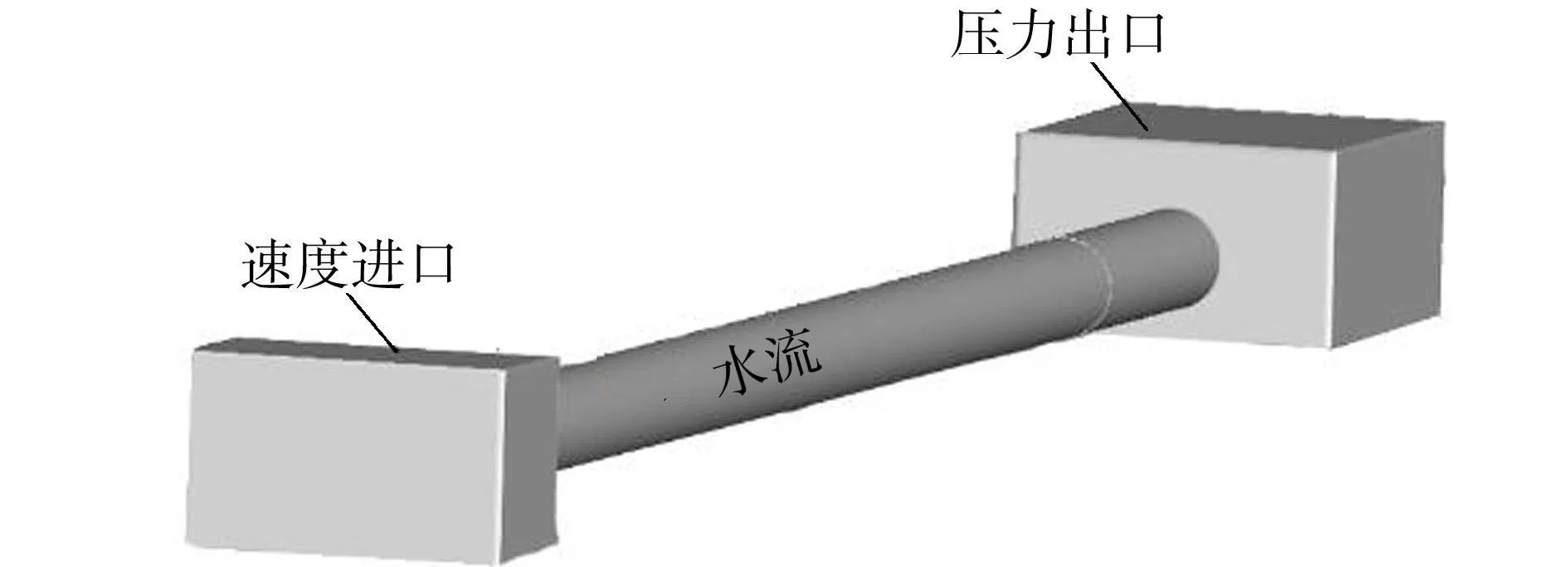
图2 三维流体模型

采用数值仿真对淡水壳菜附着下的有压输水工程的水流特性进行模拟,根据相关调研结果,有压输水建筑物中附着面积占比和附着厚度变化较为明显,本文针对面积占比和附着厚度这两种因素设置不同梯度进行数值仿真研究,如表2所示,仿真工况流量均为0.025m3/s,共有7种孔隙率。

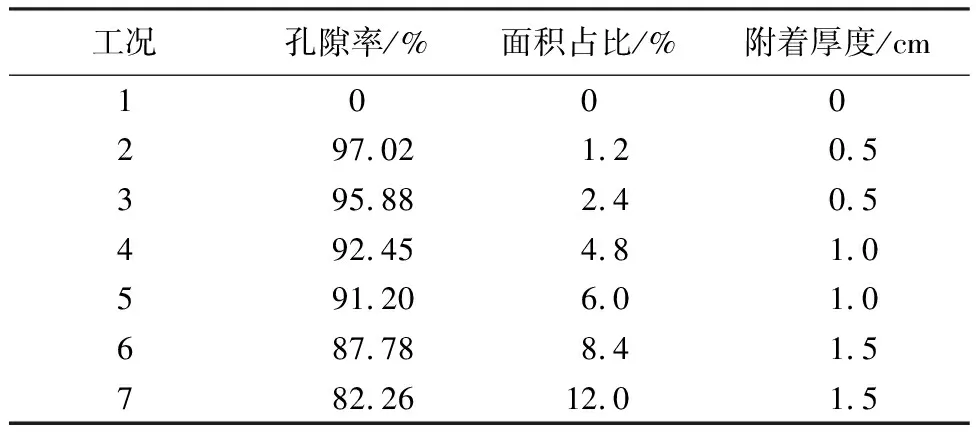
表2 数值仿真工况

2 数值模型验证

糙率可反映管壁表面影响水流阻力的各种因素,通过对比数值仿真与物理试验所得糙率,验证数值仿真模型的可靠性,根据式(3)、式(4)计算不同工况下的糙率[19];分别监测进出口断面,得到物理试验结果如表3所示。

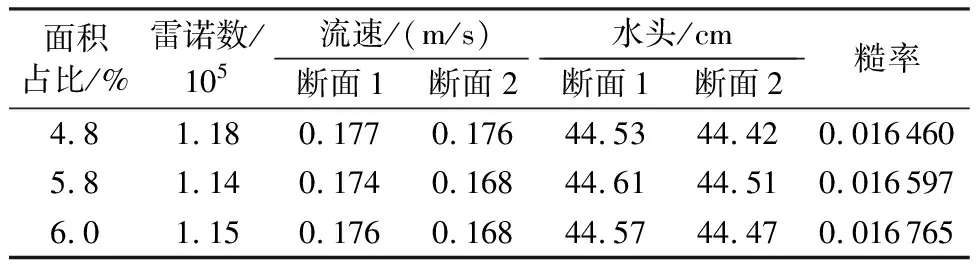
表3 物理试验糙率计算结果

(3)

(4)

式中：Z1、Z2分别为断面1、断面2处的位置水头;p1、p2分别为断面1、断面2处的压强;α1、α2分别为断面1、断面2处的动能损失系数;u1、u2分别为断面1、断面2处的流速;hf、hy、hj分别为管道总水头损失、沿程水头损失、局部水头损失;ξ为管道局部阻力系数;n为管道糙率;d为管道直径;L为测试断面距离;Q为测试流量;g为重力加速度。

由于仿真模型为理想模型且采用多孔介质近似模拟淡水壳菜附着层,以及不考虑测量误差和制造工艺精度等影响因素,因此仿真值与试验值存在一定误差,最大相对误差在10%以内(表4),符合精度要求。

表4 物理试验与数值仿真糙率对比

3 数值仿真结果分析

a.流速分布。为研究不同面积占比对水流流态的影响,提取建筑物中间纵向剖面,分析流速变化及内部水流流动特性。由图3可知,不同面积占比条件下,管道内整体上流速变化趋势相似,流速沿程减小,附着层内的局部流速明显小于管道内部。高面积占比管道内主流区域明显大于低面积占比管道,并且管道内流速受到的扰动随密度增大而增强,但流速分布较为均匀[20]。出现这种现象的原因如下：淡水壳菜的不断繁殖生长,缩小了模型过水断面,并且增大了附着密度,相当于孔隙率减小和面积占比增大,造成阻水能力增强,沿程流速减小,导致管道流速分布变化,最终对输水建筑物过流能力造成不利影响。

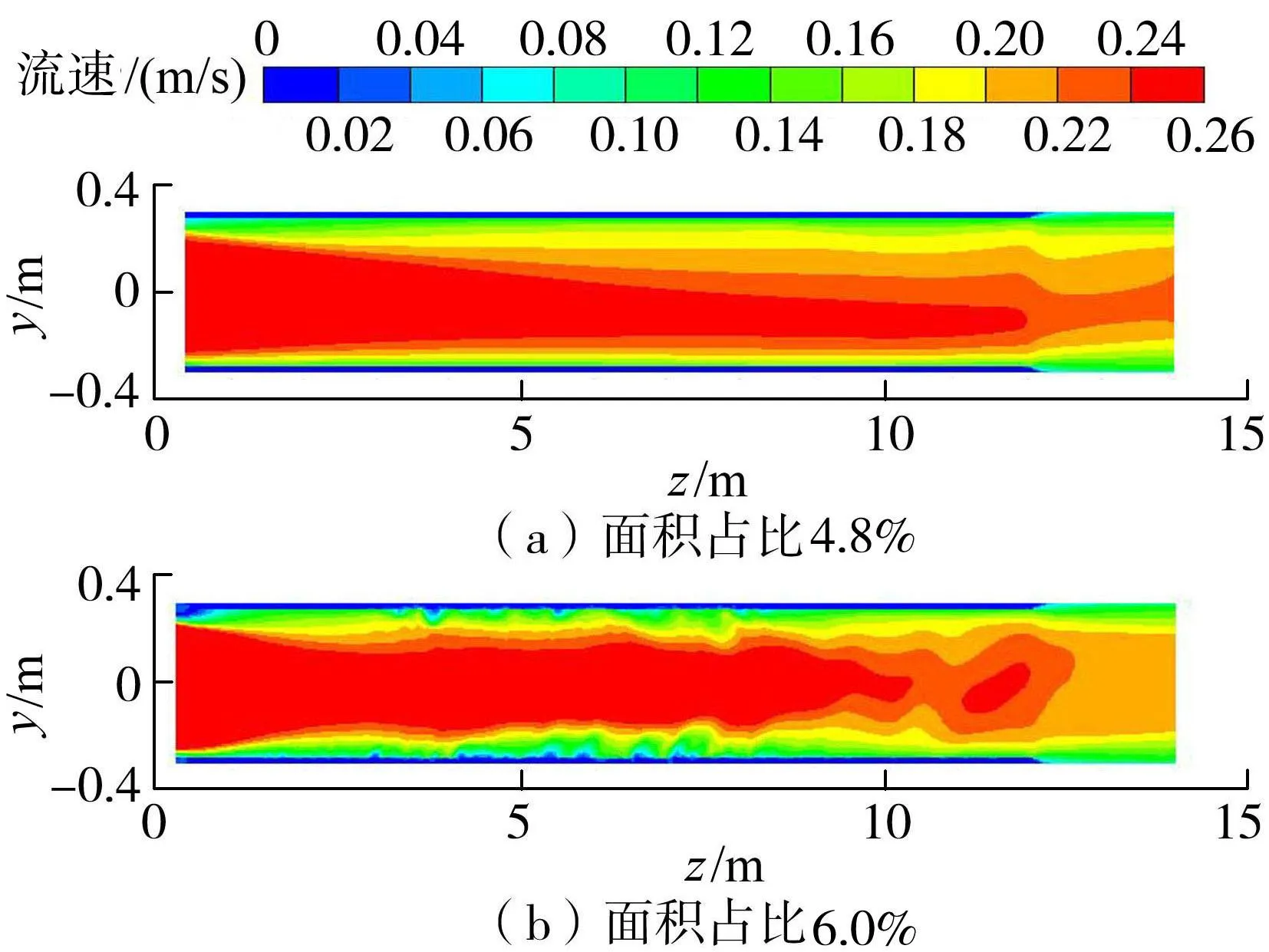
图3 不同面积占比条件下的流速仿真云图

b.湍动能变化规律。湍动能越大说明水体越不稳定,质点交换越频繁;受到壁面糙体阻水的影响,管道壁面附近的湍动能较大,在附着区域出现了湍动能极值[21]。由图4可知,不同面积占比下湍动能的沿程发展均表现出越来越对称的趋势,且面积占比为6.0%时的湍动能变化明显大于面积占比为4.8%时的湍动能,说明面积占比增大进一步增强了管道内的湍流强度。同时发现,沿程湍动能变化逐步稳定,其变化曲线呈现出上下对称结构。出现上述现象的原因为壁面附近处水流受到淡水壳菜附着的影响,造成壁面切应力较大,使得脉动流速增强和湍动强度增大[22-23];而在管道中间部位,水流湍动强度较小,水流的动量交换比较稳定。

图4 湍动能垂向分布沿程变化

c.湍动能耗散率变化规律。湍动能耗散率垂向分布沿纵向的变化见图5。由图5可知,不同面积占比下湍动能耗散率基本分布规律与湍动能相似,管道中部区域湍动能耗散率较小,壁面附近水流速度慢,但湍动能耗散率大,这说明壁面对水流的摩擦阻力较大以及流速梯度大造成湍动能耗散较快[24]。而最大流速发生在中部区域,该区域水流流动较快且流线较为集中,因此水流不断产生能量,能量耗散较少,造成水流流速梯度小,湍动耗散率也较小[25]。

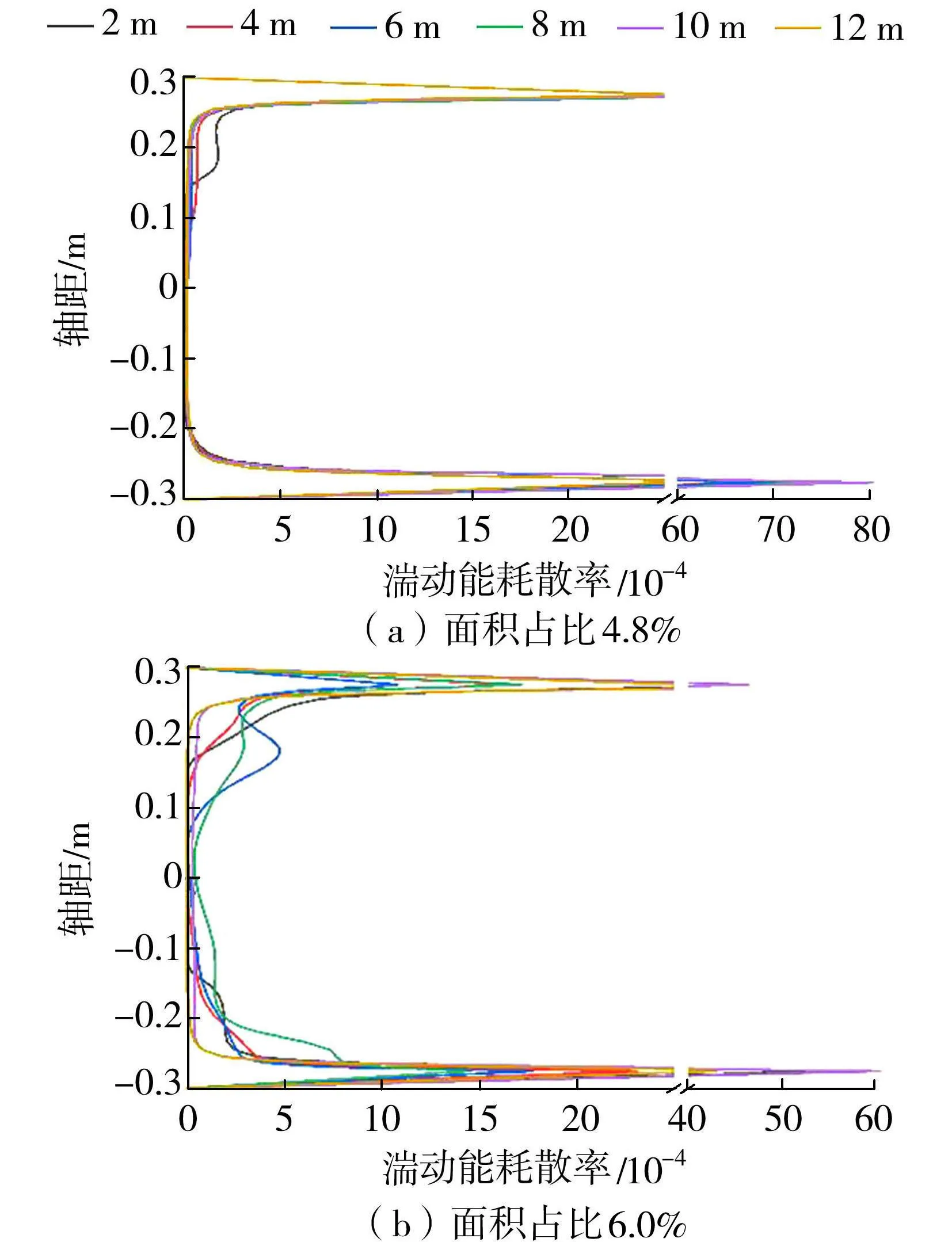
图5 湍动能耗散率垂向分布沿程变化

d.断面流速分布变化规律。断面流速垂向分布沿程变化见图6,由图6可知,不同面积占比下进口处断面流速纵向分布较为均匀,水体流动受到管道壁面糙体影响,逐步向管道中轴线集中,造成主流偏移;高面积占比造成的主流偏移影响明显小于低面积占比,但其对应的最大流速明显大于低面积占比[26]。面积占比为4.8%时断面流速分布沿程变化较为规律,但管道下部糙体对水流扰动小于上部,使得最大流速出现在管道轴线中下部;在面积占比为6.0%时进口断面流速分布与末端类似,并且进口断面流速大于末端。一方面,淡水壳菜附着造成壁面湍动能随面积占比增大,其分布情况逐步对称;另一方面,当附着面积占比增大到一定程度,淡水壳菜对管道水流的影响与缩小过水断面面积时的水流状态类似。因此,壁面淡水壳菜附着现象造成了水流向中部集中,最大流速出现在管道中轴线处[27],使得断面流速分布曲线由“对数”形变为“抛物线”形,呈现出“层流”特征[28]。

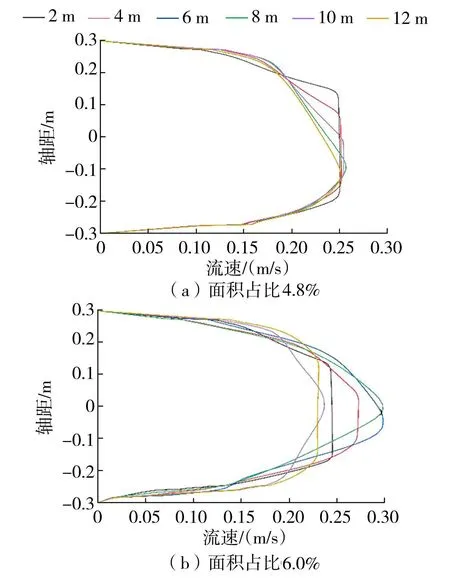
图6 断面流速垂向分布沿程变化

e.断面糙率分析。断面1、断面2分别距离管道进口2、12m,对两断面间糙率进行计算,结果见表5。进一步分析糙率与面积占比及厚度的关系,根据数值仿真成果拟合糙率经验方程并绘制三维曲面。结果表明,淡水壳菜附着造成管道糙率增加,且糙率随淡水壳菜面积占比增大而增大,在面积占比由0增大至6.0%时糙率增长了0.003951,其递增速率明显大于面积占比由6.0%增至12.0%。同时说明在较高面积占比下,淡水壳菜附着个数不再是造成糙率增大的主要因素。淡水壳菜面积占比与厚度对管道糙率产生影响,在面积占比较低时,附着厚度对糙率的影响明显小于附着厚度;而在面积占比较高时,附着厚度对糙率的影响明显大于附着厚度,通过综合两种因素对糙率的影响,初步提出有压输水建筑糙率经验公式：

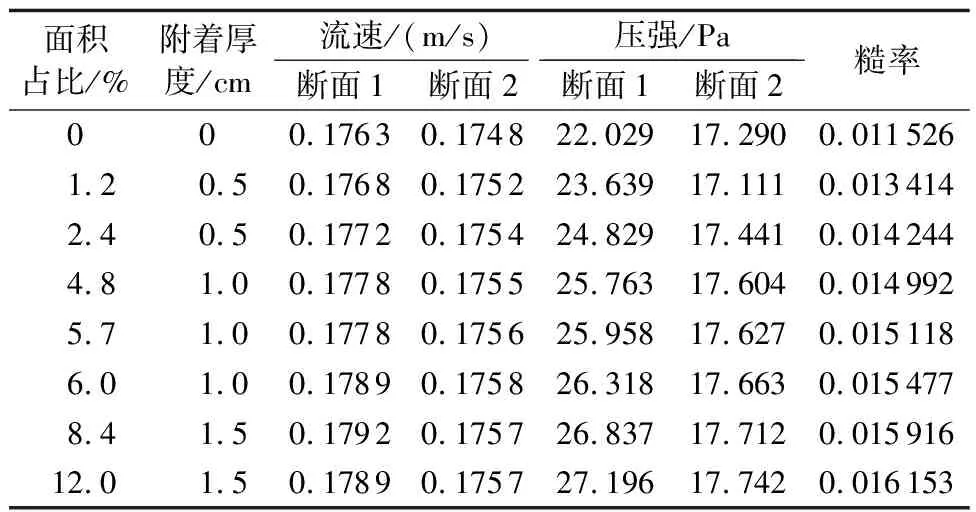
表5 不同工况下的糙率

n=0.011530+0.00138lg(8000a)b0.3137

(5)

式中：a为面积占比;b为附着厚度。

采用物理试验对式(5)计算精度进行验证,如表6所示。同等工况下式(5)计算糙率略小于物理试验结果,相对误差为8.04%～9.16%,其精度可满足使用要求。

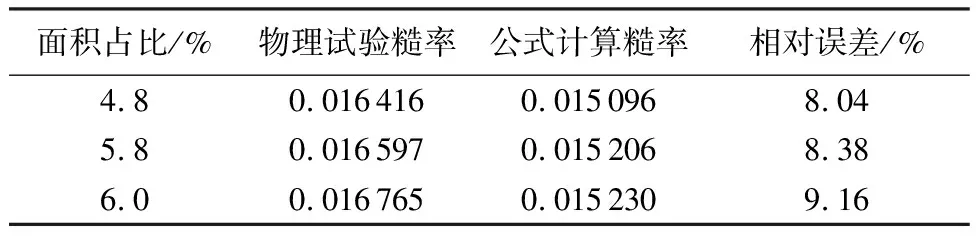
表6 物理试验与公式计算糙率对比

因多孔介质域仅可反映淡水壳菜为均匀附着的情况,为保证公式计算精度,在推广应用该经验公式时需满足以下条件：①仅适用于圆形有压输水建筑物;②淡水壳菜附着均匀,实际工程的面积占比是淡水壳菜与计算区域整体壁面的比值;③实际工程的附着厚度为计算区域间的均值;④实际工程的原始壁面糙率不得大于0.012;⑤将实际有压输水建筑物壁面淡水壳菜面积占比等比例缩小,附着厚度以过水断面为基准通过下式等效转化：

(6)

式中：Se原为原位建筑附着层面积;S原为原位建筑横断面面积;Se转为转化后建筑附着层面积;S转为转化后建筑横断面面积;λL为缩尺比。

根据文献[29]中的鱼洲-高新沙段输水隧洞实际测量数据对式(5)的推广应用进行初步验证,采用式(5)计算隧洞运行1a后的糙率为0.0153,与输水隧洞实际测量糙率0.0145仅存在5.52%的误差,初步说明该经验公式可应用于类似工程。

4 结 论

a.管道壁面附近水流受到糙体影响,湍动能和湍动能耗散率值较大,湍流强度明显随面积占比增大而增大,说明淡水壳菜附着使得有压管道内水流质点动量交换更加剧烈。

b.淡水壳菜附着会改变流场的分布,使主流转向有压管道中轴线,不同面积占比造成的影响不同。面积占比4.8%时,主流偏向于管道轴线下部;面积占比增至6.0%时,主流偏向于有压管道轴线,管内主流流速随密度增大趋势明显,断面流速分布呈现“层流”特征。

c.初步提出了有压输水建筑糙率经验公式,综合考虑了淡水壳菜面积占比与厚度的影响效应,并得到了与物理试验结果符合良好的计算结果,说明由有压输水建筑糙率经验公式所得的结果是较为可靠的。