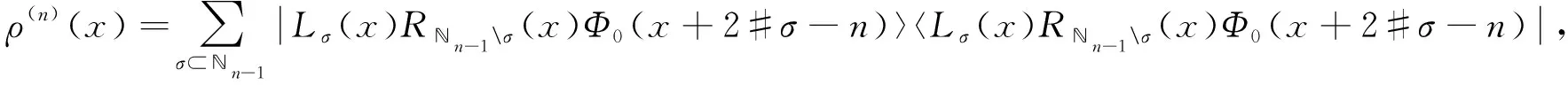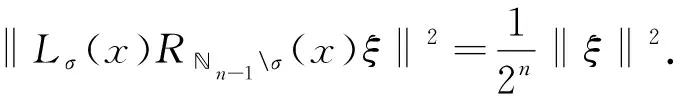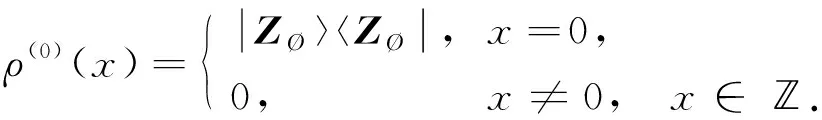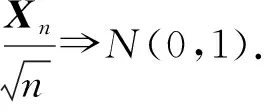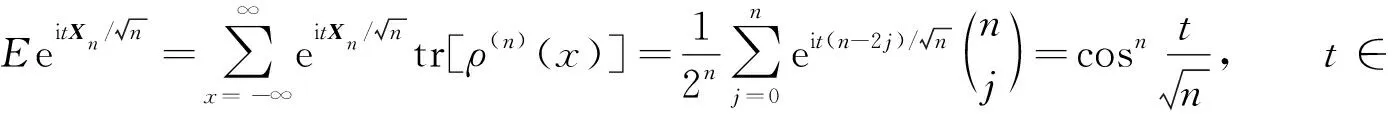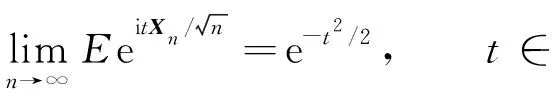基于量子Bernoulli噪声的一维时空非齐次开放量子游荡
2024-01-15于媛媛王才士
于媛媛, 王才士, 范 楠
(西北师范大学 数学与统计学院, 兰州 730070)
作为经典随机游荡的量子类似物, 量子游荡自提出以来即受到广泛关注, 并在量子信息和量子计算等领域应用广泛[1-2]. 量子游荡主要分为离散时间量子游荡和连续时间量子游荡, 针对环境的不同又分为酉游荡和开放游荡. 本文主要研究开放环境中的离散时间量子游荡. 开放量子游荡[3]是经典Markov链的精确量子类似物, 用于制定耗散量子计算算法和耗散量子态制备[4]. 在开放量子游荡中, 节点之间的转移纯粹是由与环境耗散性相互作用驱动的. 酉量子游荡和开放量子游荡的关键区别是开放量子游荡不依赖于节点之间的量子干涉, 并且它存在中心极限定理[5]. 不同于酉量子游荡, 由于局部环境的影响, 开放量子游荡的动力学是非酉的. 事实上, 开放量子游荡一步步地描述了典型的量子行为, 但它似乎显示了一个相当经典的渐近行为[6-7]. 由于经典Markov链的方法在开放量子游荡上的应用和推广, 使得其在该领域取得了许多研究成果.
QBNs(quantum Bernoulli noises)是作用于Bernoulli泛函上的湮灭和增生算子族, 满足等时典则反交换关系, 可在描述环境对开放量子系统的影响方面发挥作用[8-9]. 文献[10]将QBNs应用于开放量子游荡的研究中, 利用QBNs构造了一维整数格上具有无穷多内部自由度的离散时间开放量子游荡, 又称为一维QBNs开放游荡, 并且从概率分布的角度出发, 研究了开放量子游荡的相关性质. 文献[10]研究表明, QBNs开放游荡的演化方程受QBNs影响, 其演化方程依赖于时间的变化, 并且QBNs开放游荡具有与经典随机游荡相同的极限概率分布. 文献[11]将一维QBNs开放游荡扩展到高维的情形中, 引入了d维QBNs开放游荡(d≥2).文献[11]研究表明, 在一些初始态下, 当且仅当d维QBNs游荡有极限概率分布时,d维QBNs开放游荡具有极限概率分布, 且与d维QBNs游荡的极限概率分布一致.
文献[10]中QBNs游荡是时间非齐次的开放量子游荡, 其演化方程依赖于时间的变化. 对于空间非齐次开放量子游荡的研究目前较少. 本文旨在引入一对具有时空非齐次性的coin算子对, 进而得到一个在一维整数格上的基于QBNs的时空非齐次(即时间、 空间均非齐次)的开放量子游荡, 其演化方程不仅与时间的变化有关, 同时还与游荡者所处的空间位置有关. 并进一步研究该游荡的相关性质以及极限概率分布.
1 预备知识
1.1 量子Bernoulli噪声
Γ={σ|σ⊂且#σ<∞},
其中#σ表示集合σ的基数.设Ω={-1,1}表示所有映射ω:{-1,1}构成的集合, (ζn)n≥0表示定义在Ω上的典则投影序列, 对每个n≥0, 有
ζn(ω)=ω(n),ω∈Ω.
定义F=σ(ζn;n≥0)是Ω上由序列(ζn)n≥0生成的σ-域.设(pn)n≥0是给定的正数序列, 其中0 其中k≥1,j∈{-1,1},nj∈(1≤j≤k)满足: 当i≠j时,ni≠nj.因此得到一个概率测度空间(Ω,F,P), 称为Bernoulli空间, 该空间上的复值随机变量称为Bernoulli泛函. 设Z=(Zn)n≥0是随机变量序列(ζn)n≥0生成的Bernoulli泛函, 即 其中qn=1-pn.显然,Z=(Zn)n≥0是概率测度空间(Ω,F,P)上的一列独立随机变量. 设L2(Ω,F,P)是复值平方可积Bernoulli泛函空间, 用H表示, 即 H=L2(Ω,F,P). 用〈·,·〉和‖·‖分别表示H中的内积和范数, 并约定〈·,·〉关于第一个变量共轭线性, 关于第二个变量线性.由文献[8]可知,Z具有混沌表示性质.则Z={Zτ|τ∈Γ}是H的标准正交基(ONB), 其中ZØ=1, 且 显然H是一个无穷维的复可分Hilbert空间.易知, 对于每个n≥0,Zn=Z{n}为H的典则ONB的一个基向量. 引理1[9]对任意的k≥0, 在H上存在一个有界算子∂k:H→H, 满足‖∂k‖=1, 且 引理2[9]设k,l∈, 则下列等式成立: 且 其中I是空间H上的单位算子. 引理2表明, 量子Bernoulli噪声满足等时典则反交换关系(CAR). 参 考 文 献[10], 由于H是复值平方可积Bernoulli泛函空间, 因此对H上的算子A以及所有的ξ∈H, 如果〈ξ,Aξ〉≥0, 则称A是正的, 记作A≥0.设B(H)是空间H上的全体迹类算子构成的Banach空间,B+(H)是B(H)中正元素构成的锥, 且B+(H)中的元素称为H上的正迹类算子.若T∈B+(H)且trT=1, 则称其为H上的密度算子. 考虑张量积空间l2()⊗H, 这里l2()是上平方可和复值函数空间.由于l2()⊗H≅l2(,H), 这里l2(,H)是定义在上并取值于H的平方可和函数空间, 即 l2(, 则l2(,H)形成一个复的Hilbert空间, 定义其范数‖·‖l2(,H)由H的内积〈·,·〉l2(,H)自然诱导. 定义2[10]若映射ρ:→B+(H)满足则称其为空间H上的一个纽核(nucleus).空间H上全体纽核构成的集合记作G(H). 对于映射Φ:→H, 且以下列自然的方式定义G(H)中的一个纽核ρ: ρ(x)=|Φ(x)〉〈Φ(x)|,x∈, (1) 这里|Φ(x)〉〈Φ(x)|表示向量Φ(x)∈H在H上定义的Dirac算子.设θ∈[0,1],ρ1和ρ2为H上的两个纽核, 则θρ1+(1-θ)ρ2也是H上的纽核. 定义l2()上的典则标准正交基为{φx|x∈}, 其中 (2) 引理3[10]设ρ∈G(H), 则对于x∈, |φx〉〈φx|⊗ρ(x)为l2()⊗H上的正迹类算子, 且算子级数在迹算子范数意义下收敛, 其和是l2()⊗H上的密度算子. 引理4[10]一维QBNs开放游荡是定义在整数格上的离散时间量子游荡, 其满足下列条件: 1) 该游荡模型的态空间为l2()⊗H, 其态是l2()⊗H上的密度算子; 2) 该游荡模型的coin算子表示为 其中I是空间H上的单位算子,Ln和Rn是自伴算子; 3) 该量子游荡的时间演化方程为 ρ(n+1)(x)=Rnρ(n)(x-1)Rn+Lnρ(n)(x+1)Ln,x∈,n≥0, 因为该开放量子游荡的演化方程依赖于时间的变化, 故该游荡为时间非齐次开放量子游荡.这里整数格上的函数x→tr[ρ(n)(x)]确定一维QBNs开放游荡的概率分布, tr[ρ(n)(x)]表示n≥0时刻在位置x∈上发现游荡者的概率. 注1由于l2()⊗H是一维QBNs开放游荡的态空间,l2()⊗H≅l2(,H), 所以l2()描述该游荡的位置,H描述游荡的内部自由度.又由于H是无穷维的, 所以一维QBNs开放游荡具有无穷多个内部自由度. 由于H具有标准正交基{Zτ|τ∈Γ}, 故对每个n≥0, 可引入H的一列线性子空间: Hn=span{Zτ|maxτ≤n,τ∈Γ}, 记H-1=span{ZØ}. 引理5[10]设(ρ(n))n≥0是一维QBNs开放游荡的态的纽核序列.假设ρ(0)(x)=|Φ0(x)〉〈Φ0(x)|,x∈, 这里Φ0∈l2(,H), 且‖Φ0=1, {Φ0(x)|x∈}⊂H-1.则对所有n≥1, 有 引理6[10]设(ρ(n))n≥0是一维QBNs开放游荡的态的纽核序列.假设 定义3对于非负整数n≥0和任意的x∈, 可通过如下方式在空间H上定义两个算子Rn(x)和Ln(x): (3) 其中I是空间H上的单位算子, i是虚数单位,ξ(x)是定义在上的一个实值函数. 注2Rn(x)和Ln(x)是H上的非自伴算子, 对∀k,l≥0有如下性质: (4) 算子Ln(x)和Rn(x)分别表示粒子向左和向右移动, 故Ln(x)和Rn(x)分别称为在n≥0时刻向左移和向右移算子. 定义4令LØ(x)=RØ(x)=I,I是H上的单位算子, 对x∈, 有 (5) 定理1设ξ(x)是一个定义在上的实值函数, 则对任意的n≥0,Rn(x)+Ln(x)是空间H上的酉算子, 且满足如下关系: (6) 其次, 对任意的n≥0, 有 证毕. 命题1对x∈, 设σ,τ∈Γ, 则当σ∩τ≠Ø时, 有Lσ(x)Rτ(x)=0. 证明: 假设σ∩τ≠Ø, 则对x∈, 令m∈σ∩τ, 有 Lσ(x)Rτ(x)=Lσm(x)Rτm(x)Lm(x)Rm(x). 由式(4)有Lσ(x)Rτ(x)=0.证毕. 命题2对x∈, 设η∈B+(H), 则对所有的n≥0, 有 并且对任意的n≥0, 有 (7) 故 证毕. 设G(H)是所有映射ρ:→B+(H)的集合, 即 (8) 对于映射Φ:→H, 且中的元素ρ按式(1)定义. 命题3对任意的n≥0, 存在映射Jn:G(H)→G(H), 使得 (9) 证明: 设n≥0, 对每个ρ∈G(H), 由G(H)的定义和命题2知, 对任意的x∈, 有 由于 基于QBNs的一维时空非齐次开放量子游荡的态空间是l2()⊗H, 它的态是l2()⊗H上的密度算子.设在n≥0时刻游荡的态是由定义2、 式(2)和引理3知,有如下表示: (10) 下面描述基于QBNs的一维时空非齐次开放量子游荡的演化方程. 定义5基于QBNs的一维时空非齐次开放量子游荡模型是整数格上的离散时间开放量子游荡, 其态空间为l2()⊗H, 演化方程为 ρ(n+1)=Jnρ(n),n≥0, (11) 由于l2()⊗H是游荡模型的态空间, 易知基于QBNs的一维时空非齐次开放量子游荡具有无穷多个内部自由度. 结合命题3和定义5可知, coin算子对{Ln,Rn}(n≥0), 驱动的基于QBNs的时空非齐次开放量子游荡的演化方程等价于如下差分方程: 定理2基于QBNs的一维时空非齐次开放量子游荡具有如下纽核序列表示: (13) 证明: 由式(9)可知 再结合式(12)可得 证毕. 下面讨论基于QBNs的一维时空非齐次开放量子游荡在n≥0时刻的极限概率分布.首先固定一些符号, 以方便讨论.对所有的n≥0, 定义n-1={0,1,2,…,n-1}, 即对所有的n≥0, 都有n-1∈Γ.若n≥0,τ∈Γ, 用τ∪k简要表示τ∪{k}.对任意的n≥0, 函数x→tr[ρ(n)(x)]确定QBNs开放游荡的概率分布.定义tr[ρ(n)(x)]表示在时刻n≥0位置x∈上发现游荡者的概率. 定理3设(ρ(n))n≥0是基于QBNs的一维时空非齐次开放游荡的态的纽核序列.假设 ρ(0)(x)=|Φ0(x)〉〈Φ0(x)|,x∈, (14) 这里Φ0∈l2(,H), 且‖Φ0=1.则对所有的n≥1, 有 (15) 其中x∈. 证明: 定义Rn(x)=eiξ(x)Rn,Ln(x)=e-iξ(x)Ln.特别地, 有RØ(x)=eiξ(x)RØ=I,LØ(x)=e-iξ(x)LØ=I.用数学归纳法, 由式(12)和式(14)知: 当n=1时, 有 即当n=1时, 式(15)成立. 假设当n=k≥1时, 式(15)仍然成立, 则当n=k+1时, 有 其中 同理, 有 因此, 即当n=k+1时, 式(15)仍然成立.证毕. 引理7[10]设n≥0, 当σ⊂n-1时, 对所有的ξ∈Hn-1, 有 (16) 定理4设(ρ(n))n≥0是基于QBNs的一维时空非齐次开放游荡的态的纽核序列.假设式(14)成立, 这里Φ0∈l2(,H), 且‖Φ0=1, {Φ0(x)|x∈}⊂H-1.则对所有的n≥1, 有 (17) 证明: 由式(15), 有 由式(16)有 证毕. 定理5设(ρ(n))n≥0是基于QBNs的一维时空非齐次开放游荡的态的纽核序列.假设 (18) 对n≥1, 设Xn是x∈的随机变量, 其概率分布为 P{Xn=x}=tr[ρ(n)(x)], (19) (20) 证明: 定义映射Φ0:→H为 显然Φ0∈l2(,H), ‖Φ0=1.由式(14), 初始态(也称为l2()⊗H上的局部基态)为 定理5表明, 局部基态作为初始态时, 基于QBNs的一维时空非齐次开放量子游荡与经典随机游荡有相同的极限概率分布.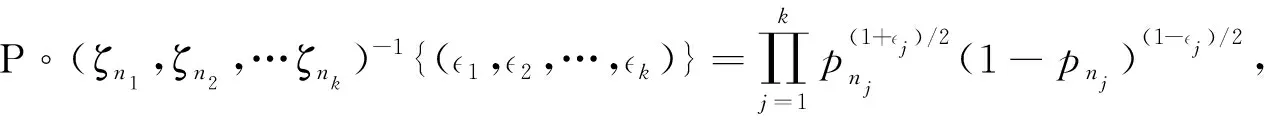
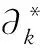
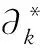
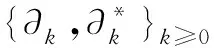
1.2 时间非齐次开放量子游荡
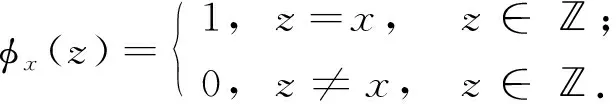


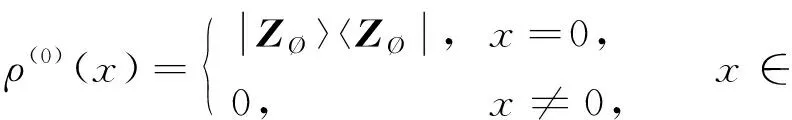
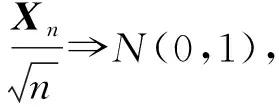
2 主要结果

2.1 一维时空非齐次开放量子游荡

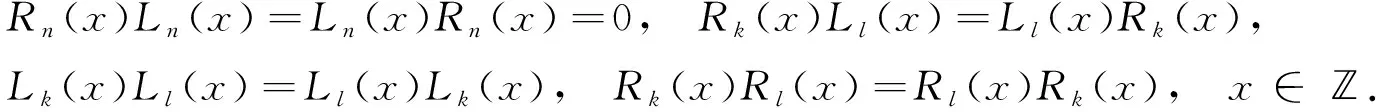
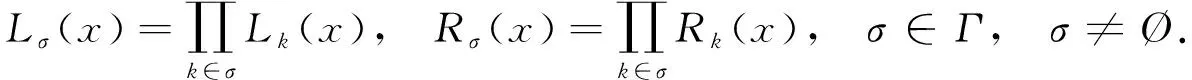
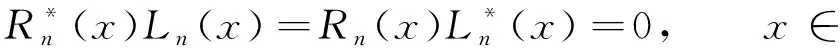

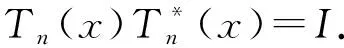
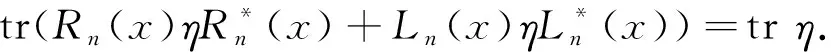


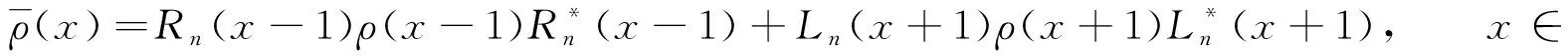

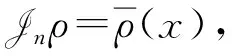




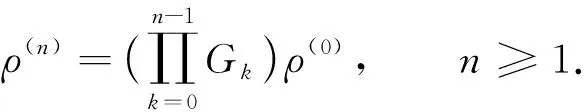
2.2 极限概率分布