一类仙人掌图的D(2)-点可区别全染色

汪银芳, 李沐春, 王国兴

(1. 兰州交通大学 应用数学研究所, 兰州 730070; 2. 兰州财经大学 信息工程学院, 兰州 730020)

0 引 言

本文所考虑的图均为简单无向连通图. 设G=(V,E)是一个图, 其中V(G)表示图G的顶点集,E(G)表示图G的边集.对∀v∈V(G), 记d(u)为顶点v的度,Δ(G)=max{d(u)|u∈V(G)}称为点u的最大度.特别地, 当d(u)=1时, 点u称为图G的悬挂点, 与u关联的边称为悬挂边.设d(u,v)=min{d(u,v)|u,v∈V(G)}为图G中点u到点v的距离.若G可以分解成恰好有一个公共顶点v的两个非空子图G1和G2, 则点v称为图G的分离点.不包含分离点的连通图称为块.仙人掌图[1]是一个每个块均为圈或边的连通图, 简记为GT.圈图Cp(p≥3)的每个点添加一条悬挂边所得到的图称为太阳图, 记作Sn, 显然n=2p.设仙人掌图G的每个块所构成的集合为B={B1,B2,…,Bm}, 分离点所构成的集合为X={u1,u2,…,un}, 每个块收缩成点所构成的顶点集为Y={y1,y2,…,ym}.以X和Y构造二部图B(G)=(X,Y), 对任意的1≤i≤n, 1≤j≤m,ui与yj相邻当且仅当分离点ui与块Bj关联, 此时B(G)称为图G的块树[2].此外, 块树中度为1的顶点对应原图中的块称为端块[2].如图1所示, 仙人掌图GT的分离点为{u1,u2,u3}, 组成仙人掌图GT的块为{B1,B2,B3,B4,B5}, 每个块对应收缩成的点集为{y1,y2,y3,y4,y5}, 构成了块树B(GT).

图1 仙人掌图GT及其对应的块树B(GT)Fig.1 Cactus graph GT and its corresponding block tree B(GT)

目前, 关于图染色问题的研究已有很多结果.例如: Burris[3]首次提出了图的点可区别边染色; Zhang等[4]在点可区别边染色的概念上, 通过限制顶点的距离提出了图邻点可区别边染色的概念, 即对于一个正常边染色满足相邻点的色集合不相同时称为图的邻点可区别边染色(也称为图的邻强边染色); 张忠辅等[5]在正常全染色的基础上, 提出了D(β)-点可区别全染色, 并给出了路、 圈、 完全图以及一些联图等的D(2)-点可区别全色数.下面给出图的D(β)-点可区别全染色的概念.

定义1[5]若图G的一个正常k-全染色f满足∀u,v∈V且1≤d(u,v)≤β时均有C(u)≠C(v), 则f称为G的一个k-D(β)-点可区别全染色(简记为k-D(β)-VDTC), 其中C(u)={f(u)}∪{f(uv)|uv∈E(G)}.将图G进行D(β)-点可区别全染色所需颜色的最小值称为G的D(β)-点可区别全色数, 简记为χβvt(G).显然χβvt(G)=min{k|G具有一个k-D(β)-点可区别全染色}.

特别地, 当β=2时,D(β)-点可区别全染色称为D(2)-点可区别全染色.

猜想1[4-5]对于阶至少为2的连通图G, 有χ2vt(G)≤μ2(G)+1, 其中μG为图G的2-距离以内的组合全度.

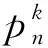
1 预备知识

引理1[5]设Pn(n≥3)是n阶的路, 则

引理2[5]设图Cn是阶数为n(n≥3)的圈, 则有

引理3[5]对于图G, 有χ2vt(G)≥Δ+1; 若G中存在距离不超过2的两个最大度点, 则χ2vt(G)≥Δ+2.

设f是图G的一个正常k-全染色, 对∀u,v∈V(G), 如果C(u)≠C(v), 则称u和v在f下是可区别的.显然如下命题成立.

命题1设f是图G的一个正常k-全染色, 若d(u)≠d(v), 则u和v在f下是可区别的.

引理4设图Sn(n≥3)是太阳图, 则χ2vt(Sn)=5.

证明: 设Cg=v1v2…vgv1(g≥3)为太阳图Sn的基本圈, 圈上每个点vi关联的悬挂边为vixi, 其中悬挂点为xi(1≤i≤g).由引理3可知χ2vt(Sn)≥5.下证Sn有一个5-D(2)-VDTC.令f为V(Sn)∪E(Sn)→{1,2,3,4,5}的一个映射.

当g=3,4,5时, 其染色方案如图2所示.

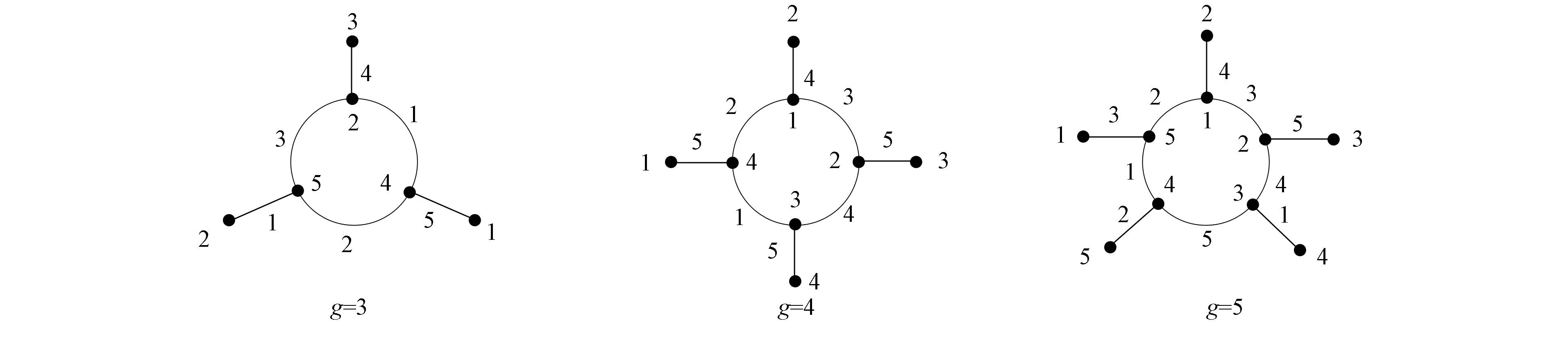
图2 太阳图的圈长为3,4,5的D(2)-点可区别全染色Fig.2 D(2)-VDTC of solar graph with cycle lengths of 3,4,5

当g≥6时, 分以下4种情形讨论:

情形1) 当g≡0(mod 4)时, 染色方案如下: 对于Cg的点vk和边vkvk+1, 若k≡1(mod 4), 则令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 则令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 则令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 则令f(vk)=4,f(vkvk+1)=3; 对于悬挂边和悬挂点, 设f(vixi)=5,f(xi)=f(vivi+1), 其中1≤i,k≤g.

情形2) 当g≡1(mod 4)时, 染色方案如下: 对于Cg的点vk和边vkvk+1, 若k≡1(mod 4), 则令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 则令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 则令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 则令f(vk)=4,f(vkvk+1)=3.其中1≤k≤g-5.而f(vg-4)=1,f(vg-3)=2,f(vg-2)=4,f(vg-1)=1,f(vg)=4;f(vg-4vg-3)=4,f(vg-3vg-2)=1,f(vg-2vg-1)=3,f(vg-1vg)=2,f(vgv1)=3.对于悬挂边和悬挂点,f(vg-2xg-2)=2,f(vixi)=5(i≠g-2);f(xi)=f(vivi+1), 其中1≤i≤g.

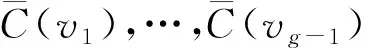
情形3) 当g≡2(mod 4)时, 染色方案如下: 对于Cg的点vk和边vkvk+1, 若k≡1(mod 4), 则令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 则令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 则令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 则令f(vk)=4,f(vkvk+1)=3.其中1≤k≤g-2.而f(vg-1)=2,f(vg)=5,f(vg-2vg-1)=1,f(vg-1vg)=3.对于悬挂边和悬挂点, 当1≤i≤g-2时,f(vixi)=5,f(vg-1xg-1)=4,f(vgxg)=2;f(xi)=f(vivi+1)(1≤i≤g).

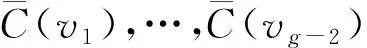
情形4) 当g≡3(mod 4)时, 染色方案如下: 对于Cg的点vk和边vkvk+1, 若k≡1(mod 4), 则令f(vk)=1,f(vkvk+1)=4; 若k≡2(mod 4), 则令f(vk)=2,f(vkvk+1)=1; 若k≡3(mod 4), 则令f(vk)=3,f(vkvk+1)=2; 若k≡0(mod 4), 则令f(vk)=4,f(vkvk+1)=3.其中1≤k≤g-3.而f(vg-2)=1,f(vg-1)=3,f(vg)=4,f(vg-2vg-1)=4,f(vg-1vg)=2,f(vgv1)=3.对于悬挂边和悬挂点,f(vg-1xg-1)=1,f(vixi)=5(i≠g-1);f(xi)=f(vivi+1)(1≤i≤g).

综上,χ2vt(Sn)=5, 结论成立.

注1在引理4的证明中, 至少存在一个悬挂点与它邻点在圈上的某条关联边染同色; 染色函数f是Sn的基本圈Cg的一个5-D(2)-VDTC.

p阶圈图Cp(p≥3)的点上任意添加悬挂边所得到的图称为破太阳图.特别地,Cp的每个点上都添加悬挂边即为太阳图.记破太阳图的基本圈为Cp=v1v2…vpv1(p≥3), 圈图的部分点上添加的悬挂边为vixi, 其中悬挂点记为xi,i∈{1,2,…,p}.

引理5设图G是一个破太阳图, 则有χ2vt(G)≤5.

证明: 设G*是G添加悬挂边后得到的太阳图, 显然,G是G*的一个子图.由引理4可知,G*存在一个5-D(2)-VDTCf, 同时也是G*的基本圈的一个5-D(2)-VDTC.因此,f|G为G的一个5-D(2)-VDTC.

2 主要结果

定理1设GT为最大度为3的仙人掌图, 则χ2vt(GT)≤6.

证明: 对仙人掌图GT的块数t进行归纳.

显然t≥2(由于t=1不存在最大度为3的仙人掌图).当t=2时, 仅有圈上关联一条悬挂边的图满足最大度为3, 不妨记该仙人掌图GT上的圈为Cn=u1u2…unu1, 悬挂边为u1x1, 其中u1是GT的分离点.先给圈Cn着色, 由引理2知, 圈Cn存在一个5-D(2)-VDTCf′, 再从集合{1,2,3,4,5}{f′(u1),f′(u1u2),f′(u1un)}中任选一种颜色染给边u1x1, 令点x1与边u1u2染同色, 从而得到图GT的一个着色方案f.在f中, 圈上的2度点均为D(2)-点可区别的.注意到d(x1)≠d(ui), 其中i=1,2,…,n.由命题1知点x1和点u1与2-距离以内所有点的色集合不同, 因此f是图GT的一个5-D(2)-VDTC.

假设结论对块数小于t的仙人掌图GT都成立.下面考虑GT中t≥3的情形, 设GT的块树中最长路为P, 对路P的端点对应GT中的端块是边或者是圈, 分以下两种情形讨论.

情形1) 存在一条路P的某个端点对应GT中的端块是边.

设该边为uv, 其中u为分离点, 由归纳假设知GT-uv存在一个6-D(2)-VDTCf′, 在f′的基础上给边uv及点v进行染色, 将f′延拓为图GT的一个6-D(2)-VDTCf.对点u的除v外的任意一个邻点x, 再分两种情形讨论.

① 点x不属于路P的某个端点对应GT中的块.

u除v外至多有两个邻点, 不妨设为点x1和x2(如果存在), 其中x1属于路P中某个端点对应GT中的块,x2不属于路P中某个端点所对应GT中的块, 且点x2不能再关联其他块, 否则与边uv属于路P最后一个端点对应GT中的块矛盾, 如图3所示.记x1除u外的其他邻点为点y1和y2(如果存在).若给点u重染色不改变x1和x2的色集合, 则可以给u重染色.因为f(u)≠f(ux1),f(u)≠f(x1),f(u)≠f(ux2),f(u)≠f(x2), 故点u可用色至少有6-4=2种; 因为f(uv)≠f(u),f(uv)≠f(ux),f(uv)≠f(ux1), 故边uv的可用色至少有6-3=3种.从而u至少有2×3=6种可用色集合.为区分u的色集合与至多3个同度点x1,y1,y2的色集合, 可从u的至少6种可用色集合中除去可能与x1,y1,y2的色集合相同的至多3种, 从余下至少3种色集合中任选一种分配给点u及边uv.因为d(u)≠d(x2),d(u)≠d(v), 故由命题1知u的色集合与点v,x2的色集合可区别.又因为f(v)≠f(uv),f(v)≠f(u), 故点v的可用色有6-2=4种,d(v)=d(x2)=1, 从v的可用色集合中除去可能与x2的色集合相同的那种, 再从余下的至少3种可用色集合中任选一种分配给点v, 则点v与2-距离的同度点x2的色集合可区别, 于是有χ2vt(GT)≤6.

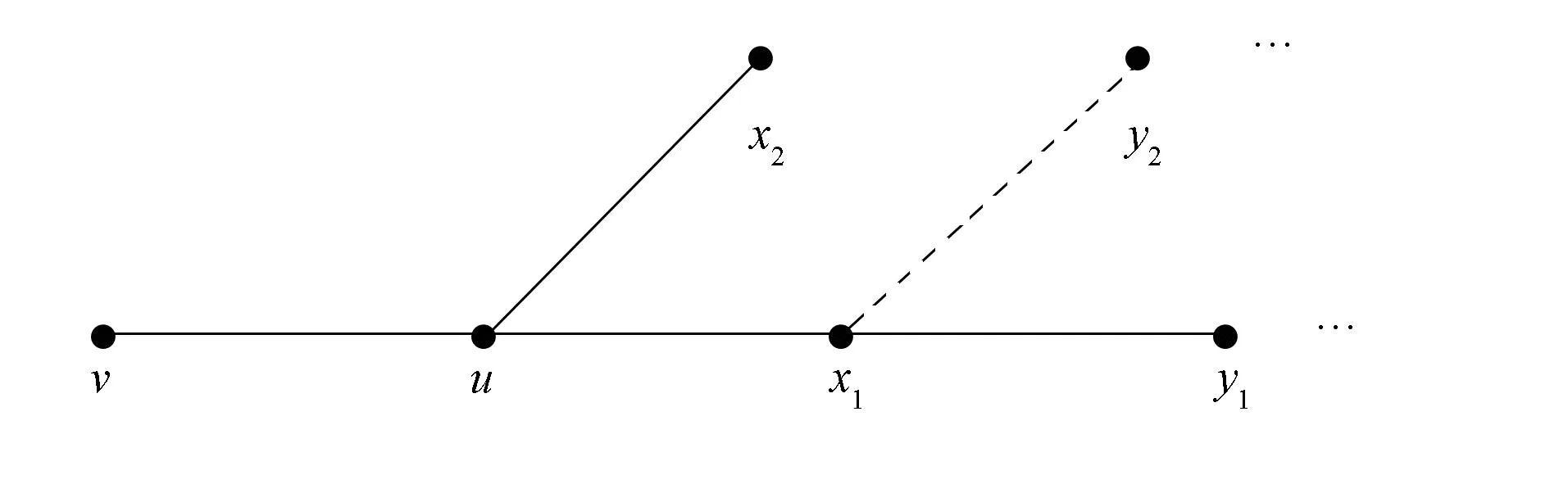
图3 x2不属于最长路Fig.3 x2 does not belong to the longest path

② 点x属于路P中某个端点对应GT中的块.

此时, 与点u相邻的点x至多有2个.

(i)x的个数为1.

此时, 根据d(u)=2或3, 以及d(x)=2或3分3种情形, 其中点u在2-距离内至多有2个同度点, 如图4所示.由于f(uv)≠f(u),f(uv)≠f(ux), 所以边uv可用色有6-2=4种, 从uv的4种可用色中除去使得点u与至多2个同度点色集合相同的那2种色, 再从剩下的至少2种可用色中任选一种分配给边uv, 再从集合{1,2,3,4,5,6}{f(uv),f(u)}中任选一种染给点v.d(v)≠d(u),d(v)≠d(x), 由命题1知点v与2-距离内的点的色集合都不同.

图4 x∈P且有1个xFig.4 x∈P and has one x

(ii)x的个数为2, 如图5所示.

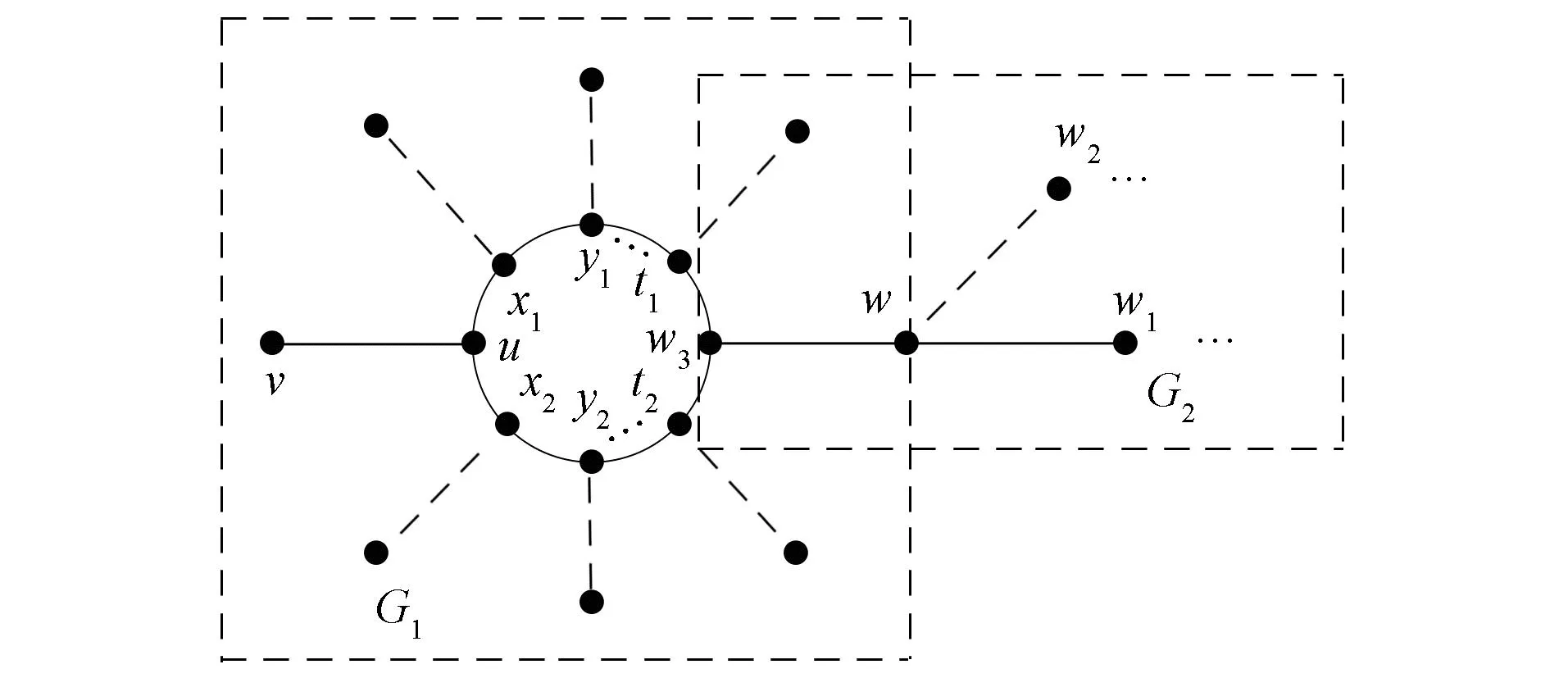
图5 x∈P且有2个xFig.5 x∈P and has two x

此时d(u)=3,u的除v外的2个邻点记为x1,x2, 记点x1,x2在圈上除点u外的邻点为y1,y2.点x1,x2,y1,y2可以关联其他的块, 但是都至多只能关联一个块, 否则uv所在块树的路就不是最长路; 且点x1,x2,y1,y2关联的块只能是边, 否则Δ>3.

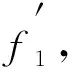
为证明GT是6色可染的, 只需验证G1和G2在上述染色方案不变的前提下粘合边w3w后仍满足2-距离之内的点的色集合不同即可.记构造得到的GT全染色为

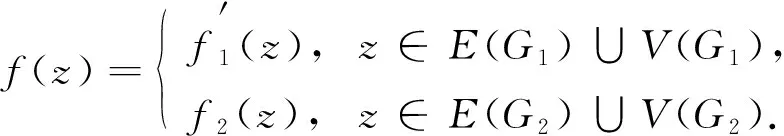
(1)

情形2) 任意一条路P的某个端点对应GT中的端块是圈.

如图6所示, 由于Δ=3, 故与最后一个圈关联的块只能为边.设u1为块树中某一条最长路的最后一个分离点,Cm=u1u2…umu1(m≥3)是GT的块树中最长路的某端点对应的端块, 点u1的除u2和um的邻点记为y, 点y除邻点u1外, 至多还有2个邻点不妨设为y1和y2.

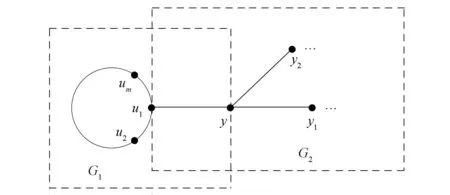
图6 最后一个块为圈Fig.6 The last block is cycle

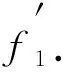
为证明GT是6色可染的, 只需验证G1和G2在上述染色方案不变的前提下粘合边zw后仍满足2-距离之内的点的色集合不同即可.记构造得到的GT的全染色为式(1).