覆冰粗糙度对翼型气动特性影响的数值研究

何志辉 张永恒 张旭耀 张沥 李泽 杨文涛

(1 兰州交通大学, 新能源与动力工程学院, 甘肃 兰州 730070;2 三峡新能源太阳山发电有限公司, 宁夏 吴忠 751999)

0 引言

近年来, 随着常规能源的日益短缺和人们对气候变化的普遍关注, 清洁能源的开发和利用日益受到重视。其中风力发电新增装机规模持续扩大, 寒冷地区因风能资源具有风速高、功率密度大的特点, 成为风电场宏观选址的首选[1]。此外,据美国南极麦克默多站统计, 其附近年平均风速高于5 m·s-1, 最高风速可达41 m·s-1。针对南、北极地区常年低温, 具有丰富的风能资源这一独特优势, 世界各国积极利用风力发电满足其供电需求[2]。风力发电机在寒冷地区运行时, 空气中的过冷水滴伴随着气流撞击在风力机叶片表面。若此时大气温度处于-10 ℃以下, 过冷水滴立即冻结形成白色不透明的霜冰; 若此时温度较高(-10～0 ℃), 过冷水滴以水膜沿着叶片表面向后移动逐渐冻结, 因为结冰过程存在溢流水, 会形成透明状的明冰或者混合冰, 附着于叶片表面[3]。叶片一旦结冰, 会在不同程度上影响其气动性能, 进而影响机组功率输出, 对机组安全运行及服役寿命带来严重挑战。

翼型结构对于叶片气动性能起着关键作用,因此确定叶片不同翼型在结冰期间性能退化的差异至关重要。基于此, 国内外学者对于翼型结冰进行了大量的数值模拟和试验研究。邓晓湖等[4]对霜冰翼型进行数值模拟, 研究发现由于结冰导致翼型失速攻角提前; 朱程香等[5]发现明冰对翼型气动特性影响较霜冰大; Han 等[6]对NREL-5MW 风力机叶尖处NACA64618 翼型积冰进行数值模拟,发现叶尖翼型前缘结冰导致风力机功率下降约8%～29%; 李岩等[7]对NACA0018 翼型进行风洞试验研究, 发现翼型的迎风面积与其表面结冰量呈正相关变化; 易贤等[8]利用MRF 方法研究1.5 MW 风力机的结冰现象, 选取叶尖至叶根处各翼段进行分析, 表明当叶尖处结明冰时, 沿叶根方向, 各翼段处的结冰形状趋于向规则的霜冰发展; 曹慧清等[9]研究翼型结冰与液态水含量的关系, 发现液态水含量与结冰质量和厚度呈正相关, 且液态水含量不影响翼型冰形生长; Gao等[10]对DU96-W-180 翼型在不同结冰条件下的动态积冰过程进行了实验研究; 郑玉巧等[11]以NH02 系列翼型族为例, 研究翼型的几何特征参数与结冰质量的相关性。在考虑叶片覆冰的同时,叶片表面不断生长的结冰颗粒可看作粗糙度, 覆冰粗糙度是叶片结冰过程中的重要参数之一, 不但影响对流换热系数和液滴局部收集效率[12], 从而影响结冰形状, 而且还会影响叶片周围的流场,进而影响叶片气动性能和机组出力。

目前对于不同参数影响下翼型覆冰形状预测及其气动特性影响分析的研究较多, 在对覆冰粗糙度的研究中, 研究重点一是集中于粗糙度对结冰形状的预测方面[13-15], 二是集中于粗糙度对其他结冰参数的影响[16-18]。研究发现, 正确模拟覆冰粗糙度对于预测翼型结冰具有重要意义[13-15]。

相对而言, 关于冰形表面粗糙度对翼型气动性能影响的研究较少, Sagol[19]将粗糙度在一定程度上进行光滑处理, 并基于此深入讨论了粗糙度对风力机气动特性的影响; 李翰涛等[20]以S809 翼型及三维小型风力机为研究对象, 研究覆冰粗糙度对于翼型及风力机气动特性的影响; 黄冉冉等[21]量化分析了不同覆冰粗糙度参数影响下的NACA23012 翼型的失速特性。叶片翼型可分为对称型和非对称型两类, 两类翼型因其曲率特征不同, 具有不同的气动特性。目前关于覆冰粗糙度对翼型气动性能的影响研究中大多选择非对称翼型, 而对对称翼型的研究并不多, 因此本文旨在研究对称(NACA0012)和非对称(NACA23012)两类翼型在相同结冰工况下,对于覆冰粗糙度的敏感性及覆冰粗糙度对其气动特性的影响。

1 数值模拟方法

1.1 结冰计算模型

叶片结冰计算模型一般包括空气流场计算、液滴收集效率计算、积冰计算及网格重构4 个部分。本文结合FLUENT 和FENSAP-ICE 软件进行结冰数值模拟研究。利用FENSAP-ICE 中液滴收集、积冰计算以及网格更新 3 个模块。通过FLUENT 耦合到FENSAP-ICE 当中进行空气流场计算。采用多时间步长几何变形的方法进行积冰计算, 将结冰事件的整个周期划分为一系列的时间间隔, 在此间隔内假定流场和集水结果不变,得到结冰计算。在更新结冰网格之后, 在前一步的基础上有限循环结冰的4 个过程。以准稳态假设的多步结冰方法达到高保真度的结冰计算。

1.1.1 空气流场计算

本文利用带有湍流模型的N-S 方程来求解流场: 划分好计算域网格后, 通过计算流体力学的有限体积法对翼型绕流流场进行求解, 得到速度矢量等参数。控制方程为低速粘性流体的N-S 方程及连续性方程:

式中,ρ为空气密度,t为时间,ϕ为运输变量,为空气速度,ϕΓ 为扩散系数,qϕ为源项。

本文采用k-ωSST 湍流模型,k-ωSST 方程如下式所示:

式中,Gk,Gω分别为湍动能k及比耗散率ω的产生项, Γk和 Γω分别为k,ω的有效扩散系数,Yk和Yω分别是k,ω的耗散项,Dω为交叉扩散项,Sk和Sω分别为各输送方程的自定义源项。

k-ωSST 模型可以准确解释结冰翼型的边界极限分离, 特别是在大攻角下的运行。并且还可以处理再循环区域, 准确预测流动分离。

1.1.2 液滴收集效率计算

拉格朗日法和欧拉法是求解过冷水滴撞击特性的主要计算方法。欧拉法在计算时可将空气流场与过冷水滴流场集合到同一套网格中, 适用于复杂结构的水滴撞击特性计算, 因此本文使用欧拉-欧拉两相流模型。水滴运动轨迹方程为:

式中,a和分别是粒子浓度和速度平均值, 公式 (6) 右侧第1 项表示作用于平均直径为d的水滴阻力, 其与相对粒子速度、阻力系数CD和液滴雷诺数Red成正比, 与惯性参数K成反比。第2项表示浮力和重力, 与局部弗劳德数Fr成反比。

式中,ρa和ρd分别为气流密度和水滴密度,Vref为相对风速,分别为气流速度和水滴速度,d为水滴直径,μa为运动黏度,L∞为特征长度,g∞为来流重力加速度。

1.1.3 结冰计算及网格重构

冰形生长计算主要是研究水滴凝结过程中的导热、对流换热等热交换及凝华、蒸发、升华等相变问题, 主要依据模型为Messinger[22]建立的热力学积冰模型。

式中,LWC为局部液态水含量,β为局部水滴收集系数,hf表示水膜厚度,为平均温度,为过冷液滴瞬时蒸发质量,为液滴撞击翼型表面瞬时结冰质量,ρf为流体密度,cf为流体比热容,为自由流温度,Lfusion为凝固潜热,ε为固体发射率,σ为玻尔兹曼常数,Levap为蒸发潜热,cs为固体比热容。本文翼型积冰没有考虑风力发电机自身防冰或除冰系统提供的热通量, 因此防冰热通量Qanti-icing可省略。

2 几何模型及算例验证

2.1 网格与计算条件

选取对称翼型(NACA0012)与非对称翼型(NACA23012)为研究对象(图1a), 弦长均取1 m,其中, NACA0012 翼型最大厚度为12%位于弦长30%处; NACA23012 翼型最大厚度为12%位于弦长29.5%处, 最大曲面为1.83%位于13%弦长处。雷诺数均为5×106。

图1 数值模拟翼型及网格。a)NACA0012 及NACA23012 翼型; b)计算域; c)清洁翼型网格划分Fig.1. Numerical simulation of airfoil shape and mesh. a) NACA0012 and NACA23012 airfoils; b) computational domain;c) clean airfoils meshing

边界条件: 计算域的左侧弧形边界, 上下边界、右侧边界都设置为压力远场, 翼型表面为无滑移壁面条件, 垂直于纸面方向的前后边界设置为对称边界(图1b)。为避免计算域尺度过小引起回流等现象影响计算结果的准确度, 计算域中左侧弧形边界距离翼型前缘为15 倍弦长, 右侧边界距离翼型前缘为20 倍弦长, 为保证无量纲壁面距离(y+)小于1, 壁面第1 层网格厚度为0.005 mm。NACA0012 及NACA23012 两种清洁翼型网格总数约2×105左右, 在ICEM CFD 中对流场域进行高质量网格划分并对翼型前缘点和后缘点附近网格进行细化(图1c)。

2.2 算例验证

采用NACA0012 翼型对本文数值模拟结果与试验结果进行对比, 以验证本文结冰数值方法的准确性。文中所对比的结冰试验数据为Shin和Bond[23]在美国NASA Lewis 研究中心进行的多组风洞试验数据其中的两组, 其计算条件为: 翼型弦长c=0.5334 m, 攻角AOA=4°, 环境温度T=-5.56℃和T=-26.11 ℃, 来流速度U=67.05 m·s-1,平均水滴直径MVD=20 μm, 液态水含量LWC=1 g·m-3, 结冰时间为360 s。

由图2 可知, 本文数值模拟的结冰形状与试验结果在一定程度上吻合度较高, 图2a 为明冰冰形, 图2b 为霜冰冰形, 所模拟的两种冰形在结冰形状和结冰极限上与试验结果基本一致, 证明本文所采取数值模拟方法的准确性, 进而可开展后续对对称及非对称结冰翼型对于覆冰粗糙度的敏感性分析及覆冰粗糙度对结冰翼型气动特性影响的对比研究。

图2 NACA0012 翼型数值模拟结果与试验数据对比。a) -5.56℃明冰形状; b) -26.11℃霜冰形状Fig.2. Comparison of numerical simulation results and test data of NACA0012 airfoil. a) -5.56°C glaze ice shape; b) -26.11℃rime ice shape

3 对称(NACA0012)及非对称(NACA23012)翼型气动性能影响分析

3.1 NACA0012 及NACA23012 翼型结冰模拟

为对比研究覆冰粗糙度对对称(NACA0012)及非对称(NACA23012)两种结冰翼型气动性能的影响, 首先要对两种翼型分别进行两种工况下的结冰计算, 得到其结冰外形, 进而研究覆冰粗糙度对两类结冰翼型在相同结冰条件下气动特性的影响。本文所设置的结冰工况条件见表1。

表1 结冰参数设计Table 1. Design of icing parameters

3.1.1 NACA0012 及NACA23012 翼型冰形及结冰网格

从图3 可知, 在不同结冰参数下, NACA0012翼型及NACA23012 翼型在-5℃时分别生成角状冰, 在-15℃时生成霜冰, 且在相同条件下, 翼型的结冰形状也极为相似。将结冰翼型导出后重新划分网格, 两种翼型在角状冰下的网格数量达到3.8×105左右, 霜冰下的翼型网格数达到2.8×105左右, 两种翼型在结冰后网格数目接近相同, 网格分布相似。

图3 NACA0012 及NACA23012 翼型不同结冰参数下的数值冰形。a)NACA0012 角状冰; b)NACA0012 霜冰; c)NACA23012角状冰; d)NACA23012 霜冰Fig.3. Numerical ice shapes of NACA0012 and NACA23012 airfoils with different icing parameters. a) NACA0012 horn ice;b) NACA0012 rime ice; c) NACA23012 horn ice; d) NACA23012 rime ice

3.2 覆冰粗糙度模型

翼型结冰过程十分复杂, 会因翼型的不同以及结冰条件的不同产生差异, 因此很难准确捕捉。关于覆冰粗糙度的数值研究中, 通常采用经过试验验证的经验公式或者假定的热力学模型进行求解。本文在覆冰表面粗糙度的设置中, 采用等效沙砾粗糙度模型, 体现结冰过程中的粗糙度效应。将覆冰粗糙度高度k叠加于翼型前缘覆冰表面, 不考虑结冰之后覆冰粗糙度对传热传质的影响, 只研究覆冰粗糙度对于结冰翼型气动特性的影响。

覆冰粗糙度常数(Cs)控制粗糙度元素是如何分布在翼型表面上, 为简化研究, 设定 Cs=0.5,即在冰层表面均匀分布等效颗粒微元。

3.3 覆冰粗糙度高度对结冰翼型气动性能的影响

研究发现, 覆冰粗糙度高度k介于 0.28～0.79 mm 之间[24], 其中, 0.5 mm 覆冰粗糙度高度为结冰计算中较为常见的覆冰粗糙度设置选择。因此, 本文对NACA0012 与NACA23012 两翼型在覆冰粗糙度高度k为0.5 mm 时的气动性能进行了数值研究。

3.3.1 覆冰粗糙度高度对霜冰翼型气动性能的影响

霜冰翼型呈流线型, 形状规则且符合翼型的气动设计, 对翼型气动性能的影响较小, 当覆冰粗糙度高度k=0.5 mm 时, 研究12°攻角下NACA0012 与NACA23012 霜冰翼型的气动特性。

由图4 可以看出, NACA0012 与NACA23012翼型前缘结霜冰时, 覆冰粗糙度高度使吸力面边界层提前发生分离, 改变边界层再附着点的位置。此外, 覆冰粗糙度高度对 NACA0012 及NACA23012 霜冰翼型流场的改变较为相似, 形成长分离泡增加翼型后缘的分离涡。

图4 NACA0012 及NACA23012 霜冰翼型有无覆冰粗糙度高度k 时的流线。a)k=0.5 mm 时NACA0012 霜冰翼型; b)无k 时NACA0012 霜冰翼型; c)k=0.5 mm时NACA23012 霜冰翼型; d)无k 时NACA23012 霜冰翼型Fig.4. Streamlines of NACA0012 and NACA23012 rime ice airfoil with and without ice roughness height k. a)NACA0012 rime ice airfoil shape at k=0.5 mm; b)NACA0012 rime ice airfoil without k; c) NACA23012 rime ice airfoil shape at k=0.5 mm; d) NACA23012 rime ice airfoil without k

图5 为NACA0012 及NACA23012 翼型在干净及有无0.5 mm 覆冰粗糙度高度时, 升、阻力系数在 0°～20°攻角范围内变化的曲线。由图5可知, 霜冰情况下, 两种翼型的升力系数同时下降, 且阻力系数同时增加, 此外, NACA0012 及NACA23012 清洁翼型的失速攻角约为16°左右,霜冰导致失速攻角提前到12°左右。研究发现, 在翼型失速攻角之前, 霜冰翼型表面具有覆冰粗糙度会使升力系数下降程度加深, 阻力系数继续增大。因此, 结霜冰时覆冰粗糙度对于NACA0012及NACA23012 两种翼型气动性能的影响都比较大。同时发现增加覆冰粗糙度后并没有改变两种翼型的失速攻角。

图5 覆冰粗糙度高度k 为0.5 mm 时两种霜冰翼型气动性能对比。a)NACA0012 霜冰翼型; b)NACA23012 霜冰翼型Fig.5. Comparison of aerodynamic performance of two rime ice airfoils with 0.5 mm ice roughness height k. a) NACA0012 rime ice airfoil shape; b) NACA23012 rime ice airfoil shape

3.3.2 覆冰粗糙度高度对角状冰翼型气动性能的影响

数值研究了在 12°攻角下, NACA0012 与NACA23012 两种角状冰翼型添加覆冰粗糙度高度k=0.5 mm 时的气动性能。由图6 可看出,NACA23012 角状冰翼型表面具有覆冰粗糙度高度时, 只是增加结冰翼型表面后缘处分离涡的宽度, 对翼型表面的分离点并没有影响, 这与之前的研究结果[20]一致。

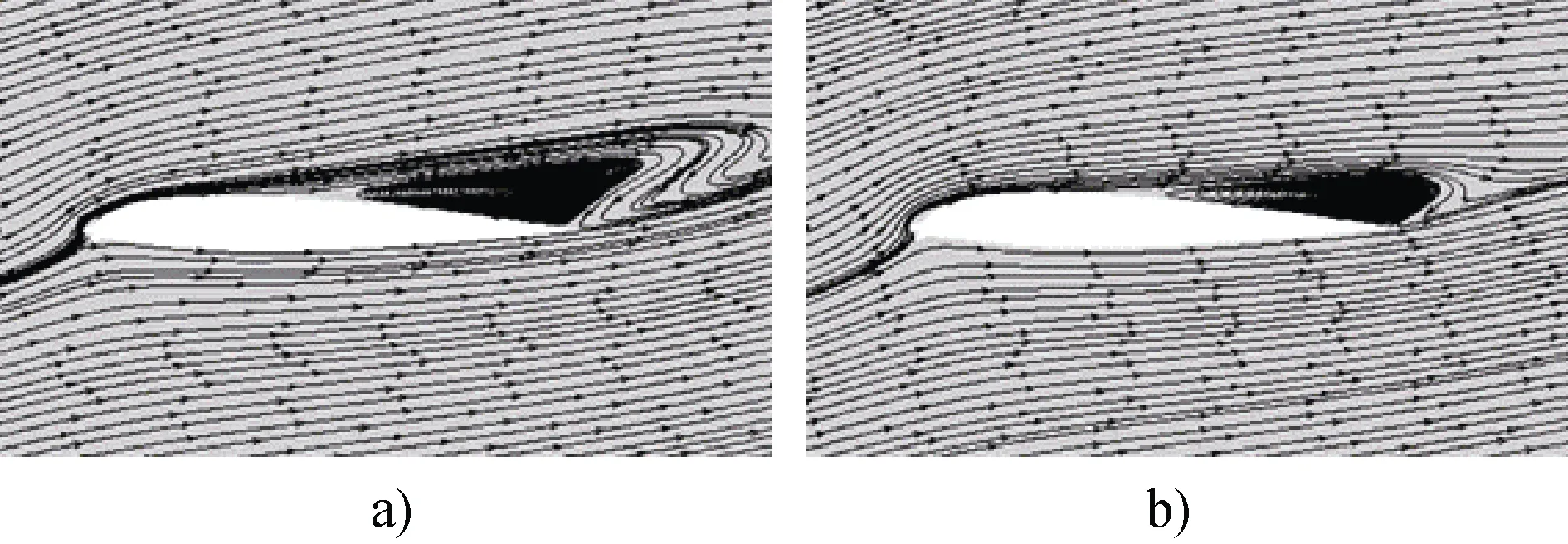
图6 NACA23012 角状冰翼型有无覆冰粗糙度高度k 时的流线。a)k=0.5 mm 时NACA23012 角状冰翼型; b)无k 时NACA23012 角状冰翼型Fig.6. Streamlines of NACA23012 horn ice airfoil with and without ice roughness height k. a) NACA23012 rime ice airfoil shape at k=0.5 mm; b) NACA23012 rime ice airfoil without k

然而, 从图7 可知, 12°攻角下, NACA0012 角状冰翼型表面有无k=0.5 mm 覆冰粗糙度高度时,翼型前缘与后缘分别出现较大的分离涡, 且分离区域逐渐发展在一起。当NACA0012 角状冰翼型表面具有覆冰粗糙度时, 翼型前后缘所出现的分离涡消失。产生这种情况的原因大致如下: 依据表1 结冰条件, NACA0012 在前缘位置生成较为尖锐的角状冰, 当翼型前方气流流过时, 会产生较大的速度, 同时NACA0012 翼型为对称翼型,与NACA23012 翼型相比, 前缘上表面位置流动过渡较差, 因此在无覆冰粗糙度时会产生如图所示的流场, 当结冰翼型表面具有覆冰粗糙度时,覆冰粗糙度起到提高流动过渡的作用, 使气流再度附着。

图8为覆冰粗糙度高度为0.5 mm 时两种角状冰翼型气动性能对比, 从图中也可以看出,NACA23012翼型结冰后, 失速攻角提前到10°左右, 添加覆冰粗糙度高度不会改变失速攻角;NACA0012 翼型结冰后, 失速攻角为10°, 而添加覆冰粗糙度高度后, 失速攻角被延迟到12°左右。

图8 覆冰粗糙度高度k 为0.5 mm 时两种角状冰翼型气动性能对比。a)NACA0012 角状冰翼型; b)NACA23012 角状冰翼型Fig.8. Comparison of aerodynamic performance of two horn ice airfoils with 0.5 mm ice roughness height k. a) NACA0012 horn ice airfoil shape; b) NACA23012 horn ice airfoil shape

为进一步研究NACA0012 翼型流场的改变是否受覆冰粗糙度高度k的影响, 在12°攻角下, 研究覆冰粗糙度高度k分别为0.25 mm、0.28 mm、0.3 mm、0.35 mm、0.4 mm、0.45 mm、0.55 mm、0.6 mm、0.65 mm、0.7 mm、0.75 mm 和0.78 mm时NACA0012 结冰翼型速度流场曲线(图9)。由图9 可知, 覆冰粗糙度高度k小于0.4 mm 时,NACA0012 角状冰翼型上表面生成分离涡, 翼型后缘无法恢复至最初的压力状态, 边界层大面积脱离叶片表面, 增加流动阻力和流动损失; 覆冰粗糙度高度k在0.4～0.65 mm 时, 表面粗糙度对结冰翼型边界层产生影响, 增加了粘性力, 使气流再度附着; 覆冰粗糙度高度k在0.7～0.78 mm时, 翼型上表面后缘处开始出现反向的分离涡,即覆冰粗糙度再次导致流动分离。

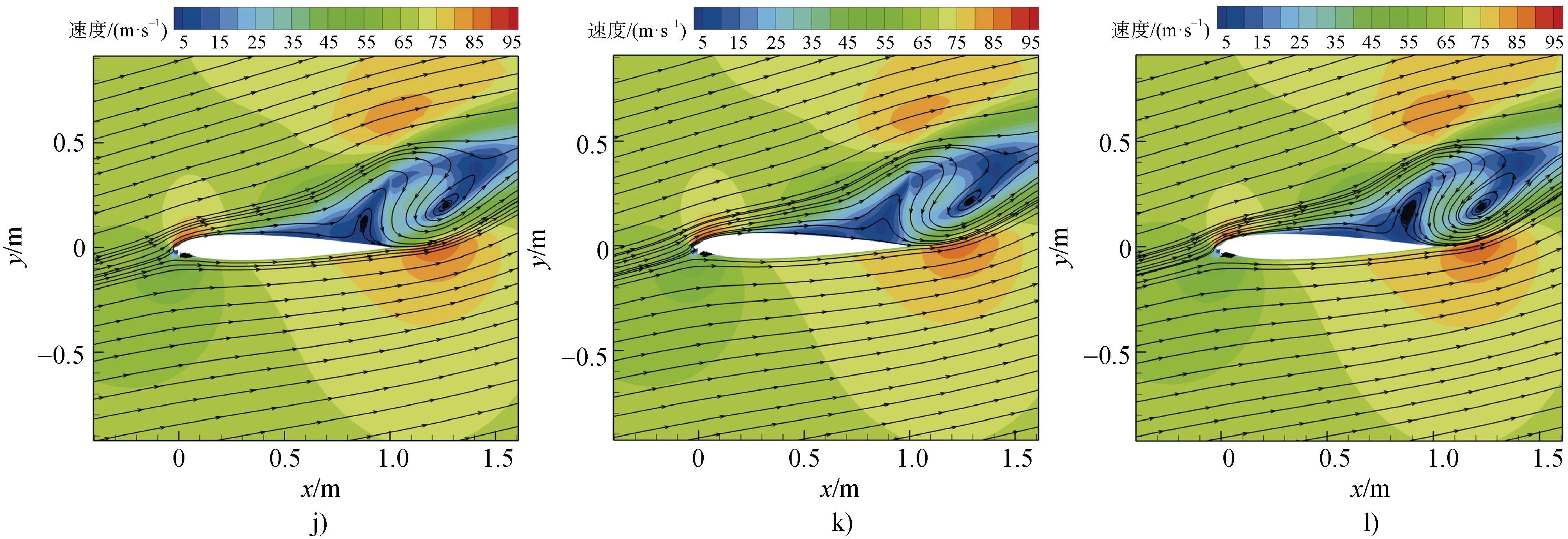
图9 NACA0012 角状冰翼型在不同覆冰粗糙度高度k 下的流线。a)0.28 mm; b)0.3 mm; c)0.35 mm; d)0.4 mm; e) 0.45 mm;f)0.5 mm; g)0.55 mm; h)0.6 mm; i)0.65 mm; j)0.7 mm; k)0.75 mm; l)0.78 mmFig.9. Streamlines for NACA0012 horn ice airfoil at different ice roughness height k. a) 0.28 mm; b) 0.3 mm; c) 0.35 mm;d) 0.4 mm; e) 0.45 mm; f) 0.5 mm; g) 0.55 mm; h) 0.6 mm; i) 0.65 mm; j) 0.7 mm; k) 0.75 mm; l) 0.78 mm

3.4 覆冰粗糙度高度对NACA0012 及NACA23012翼型气动性能的影响

选取不同的覆冰粗糙度高度, 对比分析了6°攻角与12°攻角时, NACA0012 翼型与NACA23012 翼型在不同结冰形状下的气动性能。

3.4.1 覆冰粗糙度高度对霜冰翼型气动性能的影响

在NACA0012 翼型与NACA23012 翼型结霜冰时, 研究两种翼型在不同攻角下对于覆冰粗糙度高度的敏感性。从图10 中可知, NACA0012翼型与 NACA23012 翼型结霜冰时, 两种结冰翼型随着覆冰粗糙度高度的增加, 升力系数降低, 阻力系数增加, 升、阻力系数的变化趋势相似。但是, NACA23012 结冰翼型在覆冰粗糙度高度为0.25～0.55 mm 时, 阻力系数增长速度高于NACA0012 结冰翼型。

3.4.2 覆冰粗糙度高度对角状冰翼型气动性能的影响

分别选取6°攻角、12°攻角研究NACA0012翼型与NACA23012 翼型结角状冰时, 两种翼型对于覆冰粗糙度高度的敏感性。由图11 可知,NACA0012 翼型与NACA23012 翼型结角状冰时,在小攻角下, 两种结冰翼型随着覆冰粗糙度高度的增加, 升力系数降低, 阻力系数增加, 升、阻力系数的变化趋势相似; 在大攻角下, 随着覆冰粗糙度高度的增加, 两种翼型的阻力系数增加趋势相似; 当覆冰粗糙度高度小于0.55 mm 时, 两种翼型的升力系数下降, 当覆冰粗糙度高度大于0.55 mm 以后, NACA23012 翼型升力系数缓慢降低, 而NACA0012 翼型升力系数开始小幅度增加,这与前文覆冰粗糙度对角状冰翼型气动性能影响的结论相似。可见, NACA0012 及NACA23012 翼型在两种结冰形状下的关键覆冰粗糙度高度大约为0.55 mm, 因此选取0.55 mm 的覆冰粗糙度高度研究在几个关键位置处布置覆冰粗糙度高度时,对于对称(NACA0012)及非对称(NACA23012)结冰翼型气动性能的影响。

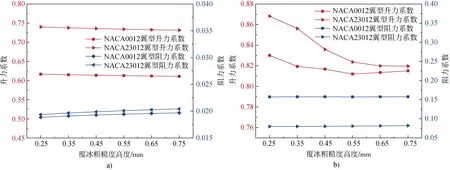
图11 两种角状冰翼型在不同覆冰粗糙度高度下的气动性能对比。a)6°攻角; b)12°攻角Fig.11. Comparison of aerodynamic performance of two horn ice airfoils at different ice roughness heights. a) attack angles of 6°; b) attack angles of 12°

3.5 覆冰粗糙度位置对翼型气动性能的影响

根据表1结冰参数对NACA0012及NACA23012两种翼型进行数值模拟, 发现两种翼型结冰极限都在弦长的13%位置处。此外, 分析两种角状冰翼型, 发现以下几个关键位置: 即翼型前缘驻点到结冰形状的最大处, 这是冰形的主要生长区,将其命名为 wing1; 前缘驻点到弦长的2.25%,此位置出现冰形拐角, 将其命名为wing2; 弦长的2.25%～6.25%处, 有细微的冰形起伏, 将其命名为wing3, 弦长的6.25%～13%处, 将其命名为wing4; 剩下位置(弦长的13%到翼型尾缘)命名为wing5。选取NACA0012翼型在霜冰和角状冰时的结冰形状, 结冰翼型覆冰粗糙度位置划分见图12。

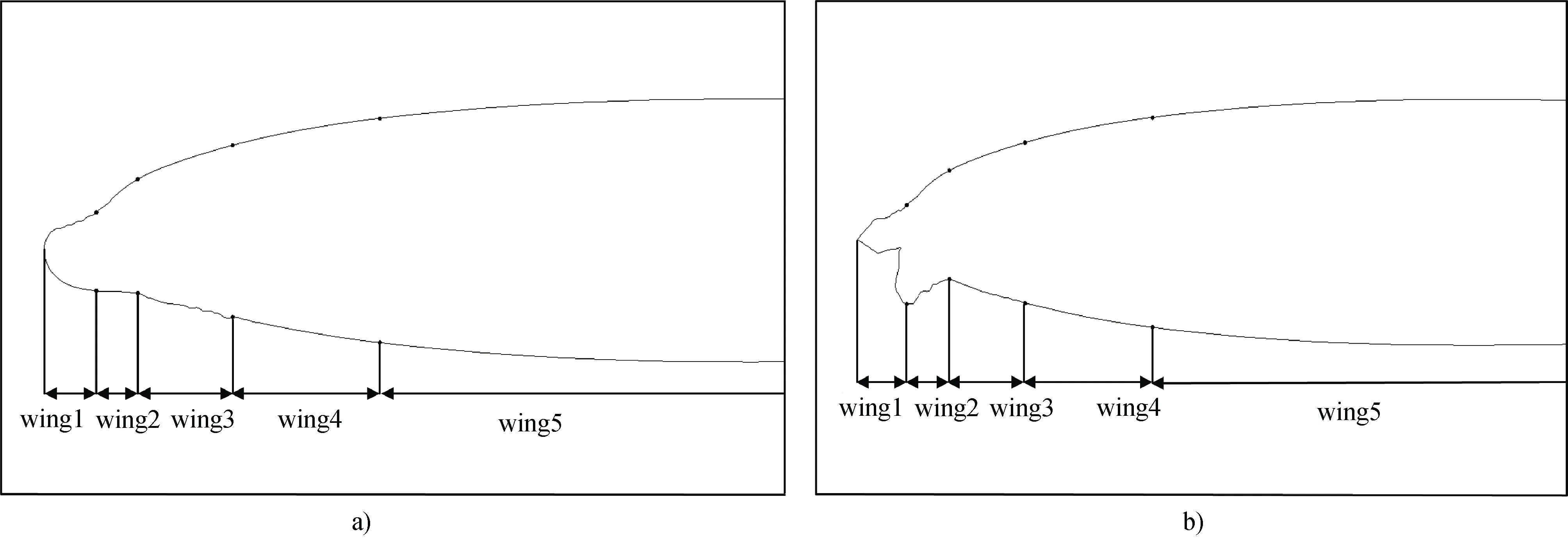
图12 结冰翼型覆冰粗糙度位置划分。a)霜冰; b)角状冰Fig.12. Location division of icing roughness for icing airfoils. a) rime ice; b) horn ice

3.5.1 覆冰粗糙度位置对霜冰翼型气动性能的影响

为研究NACA0012 及NACA23012 两种翼型在霜冰情况下不同位置布置粗糙度时的气动特性,选取6°攻角和12°攻角, 分析升力系数和阻力系数随覆冰粗糙度位置的变化曲线。

如图13 可知, 对NACA0012 及NACA23012两种霜冰翼型在前缘不同位置布置0.55 mm 高度的覆冰粗糙度时, 两种攻角下, 在wing2 位置处,两种结冰翼型升力系数增加, 阻力系数减小。这种情况可能是由于覆冰粗糙度在一定程度上改善了两种结冰翼型的气动外形, 空气动力学行为往往会增强; 在wing3 及wing4 位置处, 两种结冰翼型的升力系数缓慢降低, 且趋势接近, 阻力系数大幅增加, 且NACA23012 结冰翼型的阻力系数增加速度大于NACA0012 结冰翼型。可知, 当NACA0012 及NACA23012 两种霜冰翼型表面具有覆冰粗糙度时, 除冰形自身对于气动性能的影响外, 覆冰粗糙度带宽度越小, 对于覆冰翼型气动性能的影响越小。

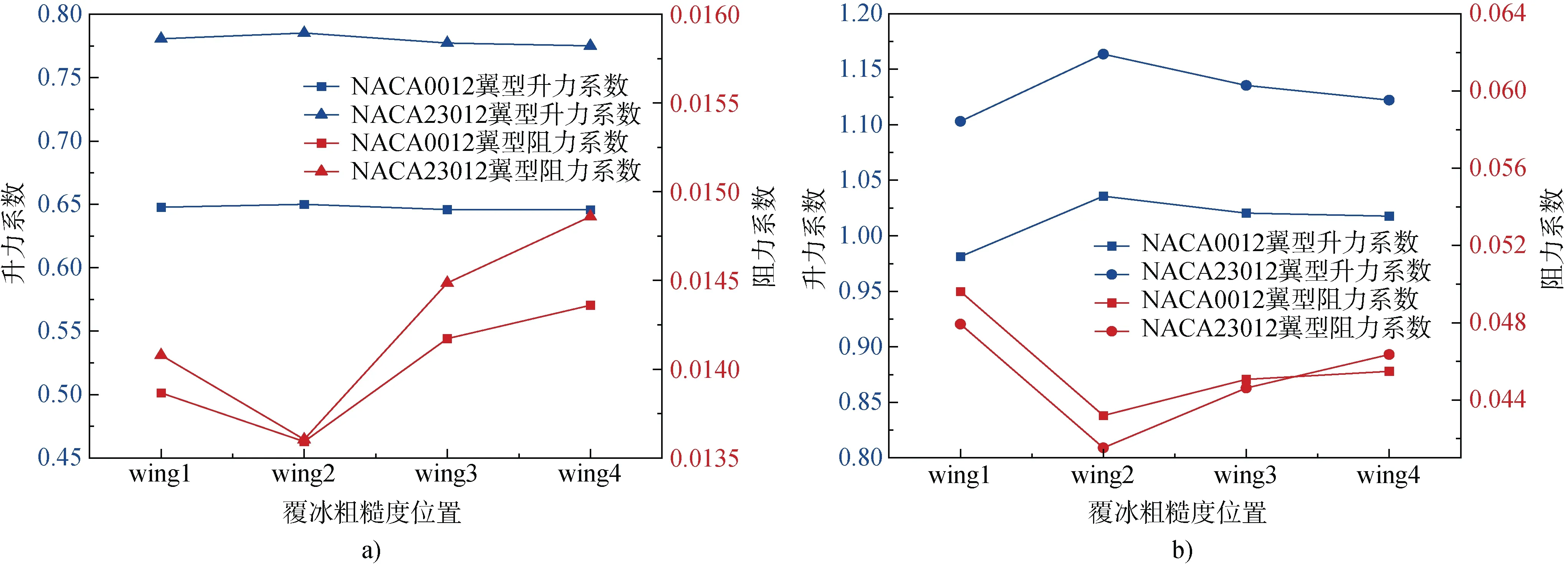
图13 两种霜冰翼型在不同覆冰粗糙度位置处的气动性能对比。a)6°攻角; b)12°攻角Fig.13. Comparison of aerodynamic performance of two rime ice airfoils at different ice roughness positions. a) attack angles of 6°; b) attack angles of 12°

3.5.2 覆冰粗糙度位置对角状冰翼型气动性能的影响

为研究NACA0012 及NACA23012 两种角状冰翼型在不同位置布置覆冰粗糙度时的气动特性,选取6°攻角和12°攻角, 分析两种结冰翼型的升力系数和阻力系数变化。

如图14 可知, 对NACA0012 及NACA23012两种角状冰翼型在前缘不同位置布置0.55 mm 高度的覆冰粗糙度时, 在小攻角下, wing1 处布置覆冰粗糙度, 两种结冰翼型升力系数降低, 阻力系数增加, wing2—wing4 位置布置粗糙度时, 升力系数缓慢降低, 阻力系数持续增加, 且NACA23012结冰翼型阻力系数的增加趋势较NACA0012 结冰翼型更为迅速; 大攻角下, NACA0012 结冰翼型在wing1—wing4 处, 升力系数持续降低, 阻力系数在 wing2 位置增大, 之后逐渐减小, 对于NACA23012 结冰翼型, 在wing1 及wing2 处升力系数增加, 随后在wing3 及wing4 处减小, 在wing1 及wing2 处阻力系数减小, 随后在wing3及wing4 处增加。此外, 12°攻角下, NACA0012结冰翼型在不同覆冰粗糙度位置处的阻力系数远高于NACA23012 翼型。

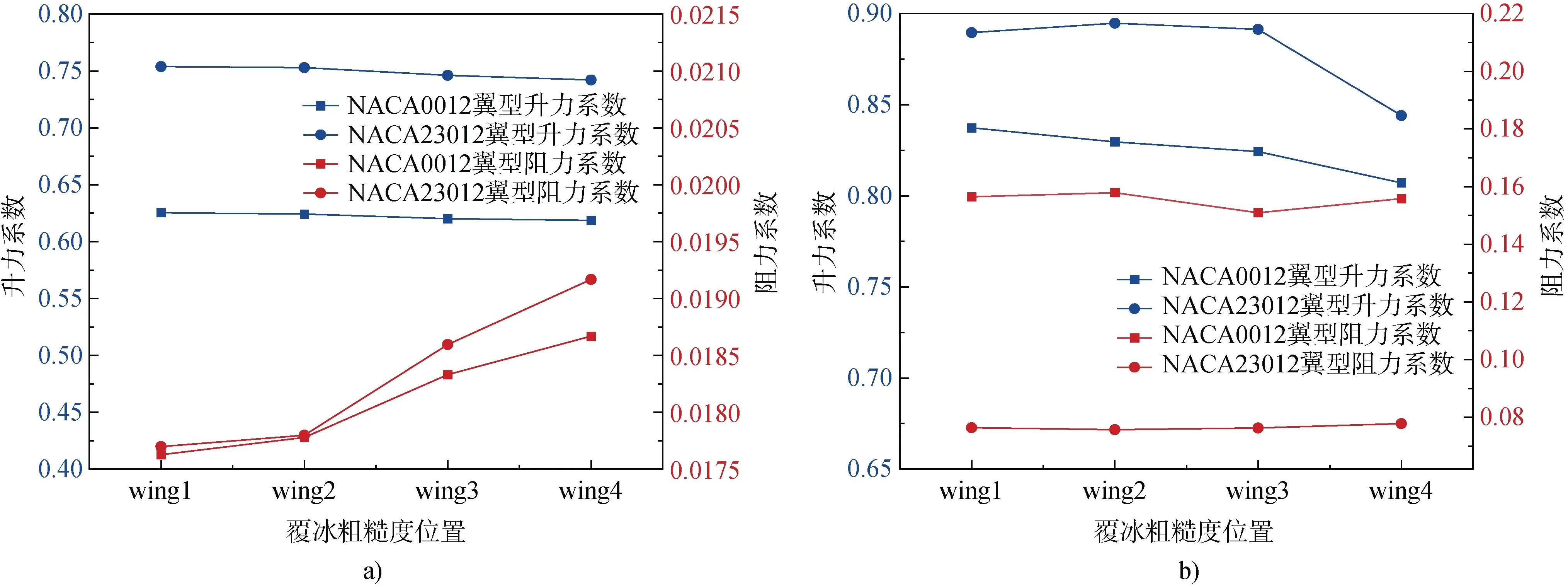
图14 两种角状冰翼型在不同覆冰粗糙度位置处的气动性能对比。a)6°攻角; b)12°攻角Fig.14. Comparison of aerodynamic performance of two horn ice airfoils at different ice roughness positions. a) attack angles of 6°; b) attack angles of 12°

由此可知, 当NACA0012 及NACA23012 两种角状冰翼型表面具有覆冰粗糙度时, wing2 处布置覆冰粗糙度, 可以改善冰形表面边界层的流动过渡, 降低对气动性能的不利影响。

4 结论

本文基于计算流体力学的数值计算方法, 对比研究了对称翼型(NACA0012)和非对称翼型(NACA23012)在相同结冰条件和粗糙度参数下的气动特性, 得出以下结论。

1. NACA0012 及NACA23012 两种翼型前缘生成霜冰时, 覆冰粗糙度对两种结冰翼型气动性能的影响显著, 使两种翼型背风面流动分离提前, 后缘分离涡结构变大; 当两种翼型前缘生成角状冰时,覆冰粗糙度对NACA23012 翼型气动性能的影响较小, 仅仅增加结冰翼型后缘分离涡的宽度; 对于NACA0012 翼型而言, 结冰翼型表面具有覆冰粗糙度时, 会延迟NACA0012 结冰翼型失速攻角。

2. 对于NACA0012 及NACA23012 两种结冰翼型而言, 在不同覆冰粗糙度高度及不同粗糙度位置时, NACA23012 霜冰翼型阻力系数增长速度均高于NACA0012 霜冰翼型, 而NACA0012 角状冰翼型在大攻角下, 在不同覆冰粗糙度高度及位置处, 阻力系数远高于NACA23012 翼型。

3. 当NACA0012 及NACA23012 两种霜冰翼型表面具有覆冰粗糙度时, 除冰形自身对于气动性能的影响外, 覆冰粗糙度位置宽度越小, 对于覆冰翼型气动性能的影响越小。

4. 当NACA0012 及NACA23012 两种角状冰翼型表面具有覆冰粗糙度时, 在冰角附近布置覆冰粗糙度, 可以使冰形表面趋于完整, 降低对气动性能的不利影响。

本文对对称翼型(NACA0012)和非对称翼型(NACA23012)在相同结冰条件和粗糙度参数下的气动特性进行对比分析, 可在一定程度上反映覆冰粗糙度对两种结冰翼型气动特性的作用规律。在冰形计算过程中, 结冰条件有一定的特殊性,可能对结果产生影响, 后续工作应进一步深入。针对结冰翼型覆冰粗糙度的研究, 能够为寒冷地区风力机叶片设计及机组性能评估提供一定的工程应用价值, 同时也能够为运行于南、北极地区的风力机叶片提供设计思路, 促进极地地区以风能发电为主的供电系统发展, 以推动极地考察与研究过程中对于清洁能源供电需求的应用。