基于补偿因子的模具型面补偿设计

乔 巍,江永恒

(中建材(上海)航空技术有限公司,上海 200120)

由于复合材料构件的刚度较大,即使较小的外形偏差,装配时往往也需要施加极大的强迫装配载荷,但这种带预应力的强迫装配行为在飞机装配规范中是明令禁止的,因此固化变形问题给复合材料构件的制造和装配带来了难题[1-2]。为了获得外形精度较高的复合材料构件,国内外复合材料结构件制造厂主要采用修整模具型面的方法,但由于缺乏复合材料固化变形的数值分析手段,因此目前主要依靠经验法估算模具型面的补偿量[3]。飞机结构通常都具有较复杂的外形,脱模后复合材料构件的变形不仅包括回弹变形、翘曲变形,甚至会产生扭曲变形,此时上述经验法就变得不可靠和具有高风险性[4]。

近年来,对固化变形控制方法的研究越来越受到重视,并取得了许多重要成果。在构件固化工艺参数优化方面,Teoh等[5]通过试验研究了真空辅助树脂传递模塑工艺,采用多级固化方法提高复合材料的固化均匀性,从而降低了L型构件的固化变形;Zhu等[6]针对L形构件的回弹变形问题,提出增加模具型面夹角的方法,模拟结果表明,回弹变形量减少了90%以上;Dong[7]针对非对称层合板的翘曲变形问题,提出了将变形量反向补偿模具型面的方法,算例结果表明,优化后的变形量减少了99%;李桂东[8]提出了一种基于型面节点变形的模具型面补偿算法,该方法首先利用数值模型预测了复合材料构件成型后的固化变形情况,并提取出固化后的构件外形,然后与理论型面进行对比,利用补偿算法和三维建模软件绘制出补偿模具型面点云数据,从而拟合得到补偿模具型面;毕凤阳等[9]建立了一种大幅面复合材料构件形状精度控制方法,该方法用模拟得到的变形量不断补偿初始模具型面来降低最终制件的变形,算例结果证明,该控制方法可以有效提高成型构件的精度。

为了获得具有高精度外形的复合材料结构件,本文提出一种基于补偿因子的模具型面补偿设计方法。以初始模具型面(理论外形)作为固化前复合材料构件的外形,通过固化变形有限元模型计算获得初始变形向量,然后将反向后的初始变形向量与补偿因子相乘,得到补偿向量,接着将补偿向量与初始模具型面叠加,从而获得补偿模具型面。建立以补偿因子为设计变量、以能够综合反映脱模后构件外形与理论外形偏差的无量纲参数(目标函数)为响应的代理模型,通过求解代理模型计算出最佳补偿因子,从而获得最优补偿模具型面。

1 复合材料结构件固化变形的数值模型

1.1 固化过程中的材料固化本构模型

在复合材料固化变形几十年的发展历程中,众多学者研究出了诸多固化本构模型[10-12]。其中Svanberg等[12]提出的Path-dependent模型获得了国内外众多学者的认可[13-14],是目前使用最广泛、最具代表性的固化本构模型。

Path-dependent本构模型中复合材料的刚度仅与材料状态有关,与温度、固化度及时间都无关,材料刚度在玻璃化转变点时发生阶跃式变化,并且在玻璃化转变点前、后的每个阶段内数值都是恒定的[13]。该模型的控制方程如下:

(1)

(2)

1.2 固化过程中的应变

(3)

(4)

式中:βj和γj分别为复合材料的热膨胀系数矩阵和化学收缩系数矩阵,ΔT和Δα分别为温度变化量和固化度变化量,α和αgel分别为固化度和凝胶固化度。

2 基于补偿因子的模具型面补偿设计

2.1 基本原理

对复合材料构件的理论外形、模具型面、固化前构件外形以及脱模后构件外形的状态进行说明和解释。模具工艺类型决定了复合材料构件的理论外形,以复合材料U型梁为例,采用阳模工艺时取U型梁三维理论模型的内形面作为理论外形,采用阴模工艺时取外形面作为理论外形,如图1所示。按照现有的制造工艺,模具型面通常以构件的理论外形为依据,因此模具型面与理论外形保持一致。固化前,将复合材料预浸料逐层铺放在模具表面,预浸料与模具型面贴合,因此固化前构件的外形与模具型面一致。由于固化过程中热收缩、化学收缩等因素的影响,导致脱模后构件的形状发生变化,因此脱模后构件的外形与模具型面不一致。模具型面和构件外形之间的关系如图1所示。

图1 理论外形、模具型面及脱模前后构件外形之间关系图

根据上述分析可知,如果直接以复合材料构件的理论外形作为模具型面,由于复合材料的固化变形,那么脱模后构件外形与理论外形之间存在外形偏差。为了提高脱模后构件的外形精度,本文提出一种基于补偿因子的模具型面补偿设计方法,目的是为了寻找到一个符合要求的目标外形,该目标外形预先考虑了固化变形的影响,使脱模后构件外形与理论外形之间的偏差量较小。

2.2 优化策略与步骤

本文提出了基于补偿因子的模具型面补偿设计优化策略,该优化策略的具体步骤如下。

第1步,计算初始状态下复合材料构件的固化变形。以初始模具型面S0(理论外形)作为固化前构件的外形,通过有限元分析(FEA)计算获得构件的初始变形向量D0,如图2所示。在有限元计算中,模具型面和构件的外形状态以全局坐标系下离散化节点坐标表示。将任一节点i在初始模具型面S0上的坐标表示为(xi,yi,zi),将初始变形向量D0表示为(Δxi,Δyi,Δzi)。选取几个重要节点作为对比点,其初始偏差位移Hk,0为:

(5)

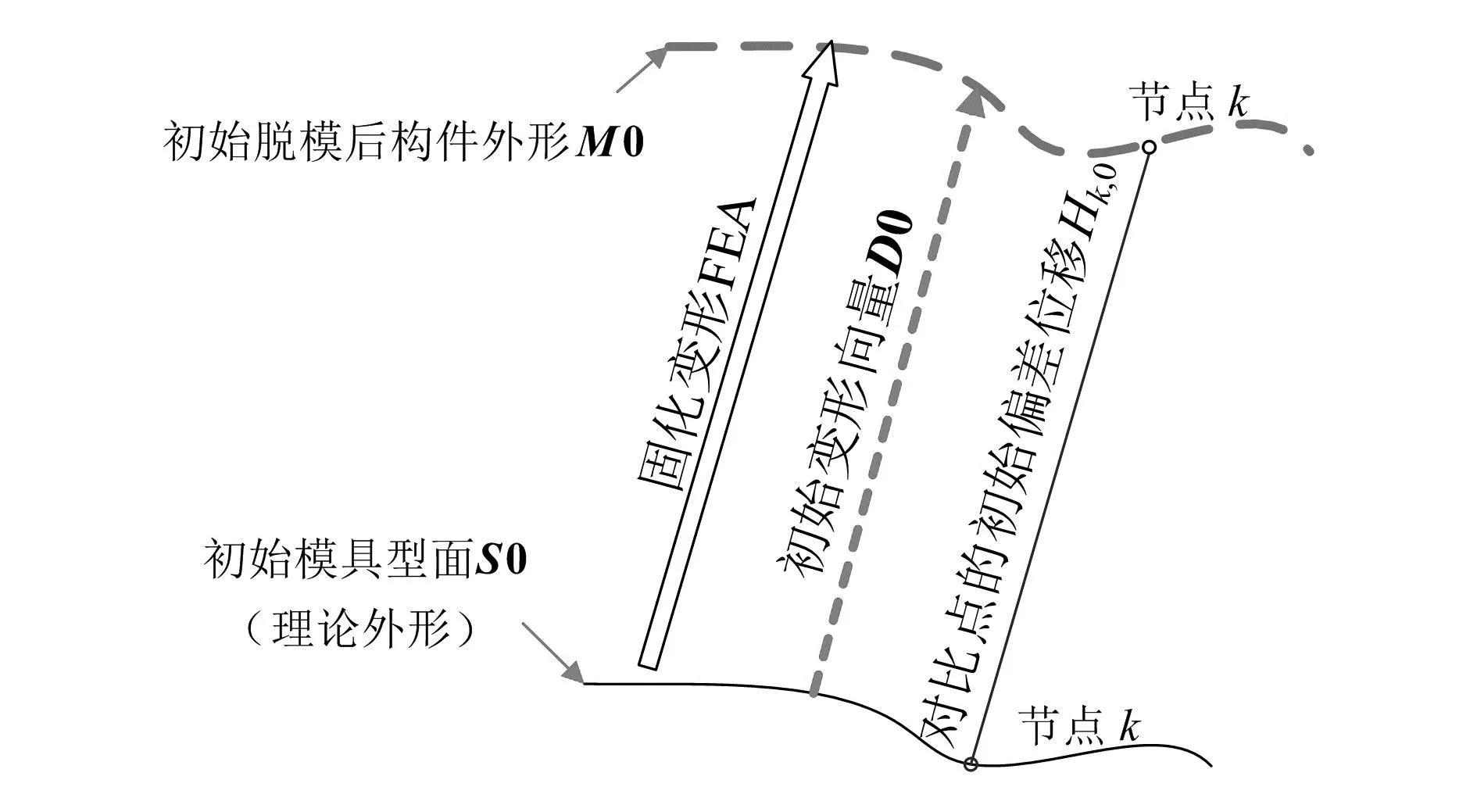
图2 初始状态下固化变形的计算流程图

式中:k为对比点的编号,Δxk、Δyk、Δzk为对比点k在3个主方向上的变形量。

第2步,建立以补偿因子为设计变量的代理模型。先对初始模具型面进行补偿设计,补偿向量D1的定义为:D1等于补偿因子μ与初始变形向量D0乘积的反向,即:

D1=-D0×μ

(6)

然后,将补偿向量D1与初始模具型面S0叠加,得到补偿后模具型面S1,如图3所示。得补偿后模具型面S1上节点i的坐标为:

(7)

图3 补偿状态下固化变形的计算流程图

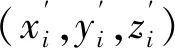
(8)

定义一个能够综合反映脱模后构件外形M1与理论外形偏差程度的无量纲参数Fobj:

(9)

式中:NH为对比点的数量。参数Fobj能够表征脱模后构件外形M1与理论外形T之间的外形偏差程度,当Fobj较小时,表明M1与T之间的偏差小;反之,则表明M1与T之间的偏差大。

由于补偿因子的取值决定了脱模后构件的外形精度,因此本文将模具型面补偿问题转化成以补偿因子μ为设计变量、以Fobj最小为目标的优化问题。该优化问题的数学模型如下:

(10)

为了提高求解效率,引入代理模型技术,建立补偿因子-目标函数代理模型。从补偿因子μ的设计空间内选取样本点集,然后依次进行固化变形有限元分析计算,从计算结果中获得目标函数Fobj的值。在实际使用中发现,采用二阶多项式建立的代理模型能够取得较好的拟合效果。本文构建的二次多项式如下:

Fobj=aμ2+bμ+c

(11)

式中:a、b、c为二次多项式的待定系数。求取二次多项式的极小值,即可求得最佳补偿因子。将最佳补偿因子代入式(7),可获得最佳补偿型面。

3 算例

3.1 材料与结构

以某飞机复合材料U型梁为例进行说明。复合材料U型梁的几何尺寸如图4所示,内侧曲率半径为1 500 mm,长度为1 600 mm,宽度为100 mm,高度为50 mm,铺层为[0/45/90/-45]2s。按照上述尺寸进行铺贴、封装及固化,完成固化并脱模后再根据真实尺寸切边、开孔等。所用复合材料的牌号为AS4/8552,具体材料性能见文献[14]。模具材料为合金钢,采用阴模手工铺贴预浸料,再经热压罐固化成型工艺制备。

图4 复合材料U型梁的几何参数

由于复合材料U型梁的厚度较小(为2 mm),固化过程中温度差很小,因此假设固化过程中U型梁内部温度与热压罐的固化温度一致。采用应力-变形分析模型计算时,固化本构模型采用改进的Path-dependent模型。根据结构和边界条件的对称性,在此取二分之一几何模型进行建模。

网格单元选择三维实体单元C3D8R,厚度方向上划分4层网格,缘条的长度方向和宽度方向分别划分28个网格和4个网格,腹板的宽度方向划分7个网格。U型梁有限元模型共3 680个单元,4 920个节点。检验网格的依赖性,结果证实更小尺寸的网格对计算结果的影响很小。在U型梁的中间和端面的内外缘条上分别选择4个节点,共8个对比点,如图5所示。

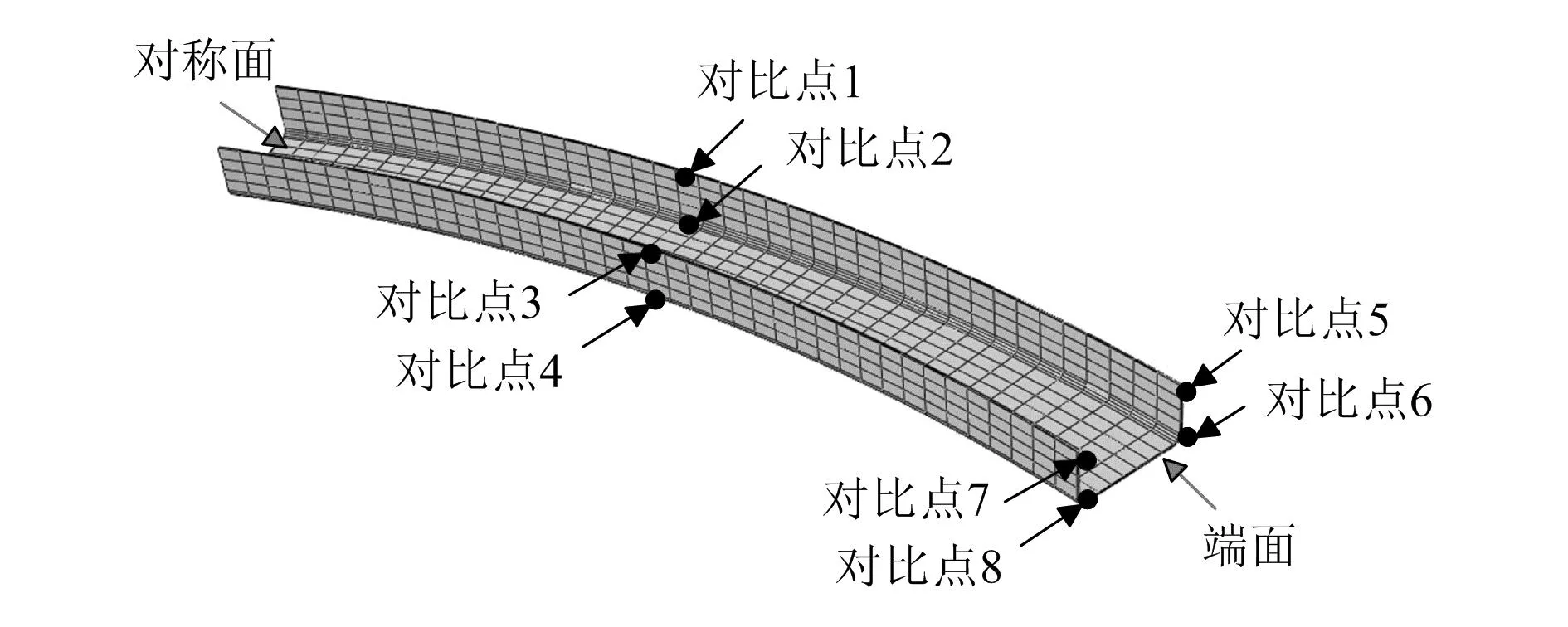
图5 对比点的选取

3.2 优化结果与讨论

首先,以初始模具型面(理论外形)作为复合材料U型梁的外形面,建立U型梁有限元模型并进行固化变形分析,获得脱模后固化变形,计算结果如图6所示。界面摩擦力对U型梁固化变形的影响很小,主要是因为U型梁抗弯刚度较好。从图中可以看出,U型梁内外缘条与腹板的夹角变小,这说明缘条处发生了回弹变形。端面处表现出非常复杂的翘曲和扭转变形,这是由于U型梁本体具有一定的曲率,梁发生了整体回弹变形,且缘条的回弹变形与梁的整体回弹变形进行耦合,因此呈现出非常复杂的变形。U型梁的最大变形量为9.896 mm,位于端面处内缘条的最上部。

图6 复合材料U型梁脱模后的变形云图(单位:m,变形放大系数:5)

在有限元软件中输出U型梁外形面上所有节点的坐标和变形量,输出计算结果的格式如图7所示。图中第2列～第4列为变形前的坐标,即初始模具型面S0的节点坐标;第5列～第7列为变形量。从图中提取出对比点的变形量,可计算出对比点的偏差位移。

图7 有限元软件结果报告的格式

建立目标函数-补偿因子代理模型。补偿因子μ的取值范围为0～1.5,均匀取16个点(间隔为0.1)。给定补偿因子μ的取值时,根据式(3)和图7中初始模具型面S0的节点坐标,可以计算出补偿后模具型面D1的节点坐标。采用MATLAB软件编写程序,完成补偿后模具型面节点坐标的计算。三维结构软件读取这些节点的坐标后,采用曲面重构方法生成补偿后的模具型面,如图8所示。将补偿后模具型面导入有限元软件,重建固化变形后的有限元模型,并计算出脱模后的构件外形。从计算结果中提取出对比点的变形量,计算出对比点相对于理论外形的偏差位移Hk,从而获得此时目标函数Fobj的值。

补偿因子和目标函数的计算结果如图9(a)所示,由图可以看出,当μ≤0.9或μ≥1.1时,Fobj与μ呈线性关系,可采用一次多项式拟合;当0.9<μ<1.1时,Fobj与μ呈非线性关系。在0.9～1.1新增2个样本点后,结果如图9(b)所示,由图可以看出,Fobj与μ之间的函数关系可采用二次多项式拟合,拟合式如式(12)所示。拟合优度R2接近于1,表明拟合效果良好。对式(12)取极值,计算出μ=0.985时目标函数值最小,此时补偿后模具型面即为最优模具型面。

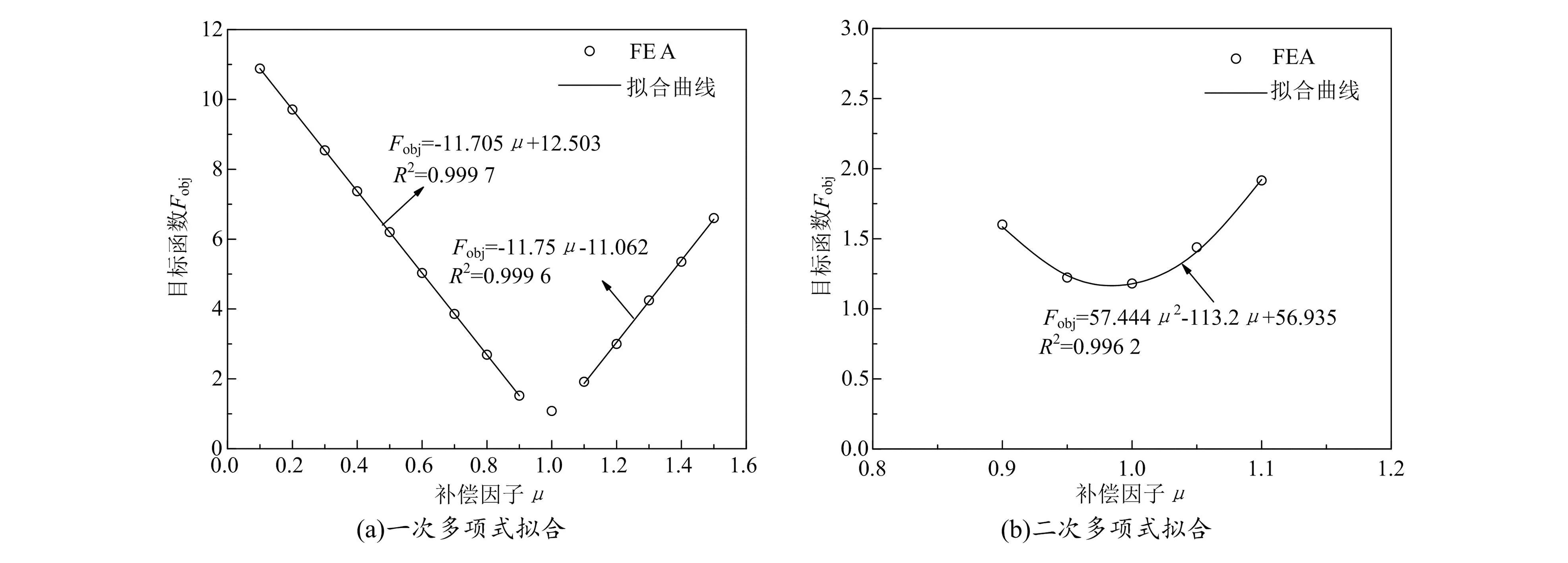
图9 建立补偿因子-目标函数的代理模型

Fobj=57.444μ2-113.2μ+56.935

(12)

补偿因子μ取值0.985,获得优化后的模具型面,如图10所示。表1给出了优化前、后对比点的偏差,由表可知,优化前的最大偏差为9.869 mm,优化后的最大偏差为0.660 mm,减少了93.33%。表中计算结果表明,除了对比点2,其他对比点的偏差均减少了90%以上,这证明本文的模具型面补偿设计方法具有显著的优化效果。

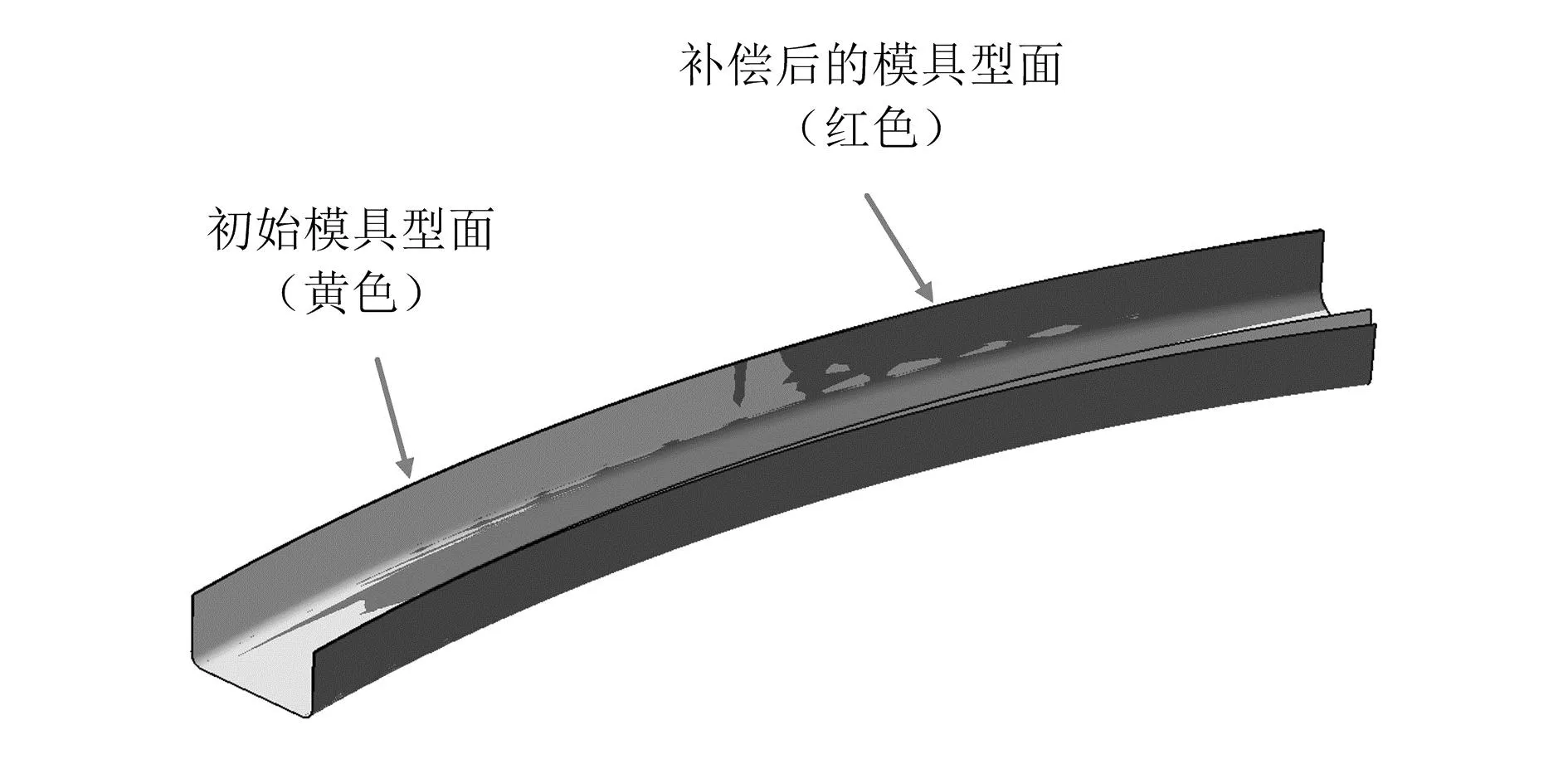
图10 优化后的模具型面(补偿因子:0.985)

4 结束语

本文对基于补偿因子的模具型面补偿设计方法进行了研究,定义了模具型面的补偿策略,将初始变形向量反向后与补偿因子相乘,得到补偿的向量与初始模具型面叠加,获得补偿后模具型面。将模具型面补偿问题转化成求解最优补偿因子的数学优化问题,为了提高求解效率,引入代理模型技术。以补偿因子为设计变量,以一个能够综合反映脱模后构件外形与理论外形偏差的无量纲参数(目标函数)为响应,建立了补偿因子-目标函数代理模型。U型梁算例结果表明,优化后构件外形的偏差位移减少了90%以上,证明本文所提优化方法获得了满意的优化结果。