基于微分同胚变换的智慧交通锥反步编队控制

张佳乐，焦生杰*,2，王玥琳，易小刚

（1.长安大学 公路养护装备国家工程研究中心，西安 710064，中国；2.江苏集萃道路工程技术与装备研究所有限公司，徐州 221004，中国）

交通锥作为道路养护作业中必不可少的工具之一，其在引导车流，保证正常道路养护作业方面有着重要作用。目前，市场上主要有2 种摆放方式[1-2]：一种是人工摆放交通锥，另一种是车辆收集放置交通锥。其中，人工摆放耗时耗力，增加了工人摆放过程中发生交通事故的风险。现有的交通锥放置设备无法实现交通锥斜线摆放以及曲率大的摆放要求，尤其在回收交通锥的过程对驾驶员有一定的技术要求。为了解决上述难题，智慧交通锥逐渐走入人们的视线中，其由一个标准的交通锥模型和一台Irobot Roomba 机器人组成，同时配备了各种传感器去收集周围环境的数据，可进一步解决当前交通锥有序摆放和回收问题。因此，针对交通锥编队摆放和回收问题展开研究具有理论和应用价值。

编队控制是智慧交通锥系统控制中的一个关键问题。多移动机器人编队控制出现了一些方法，如：行为法[3-4]、虚拟结构方法[5-6]、人工势场法[7-8]、领航跟随方法[9-11]。在行为方法中，将几个期望行为分配给每个机器人，得到的控制动作是所有可能行为的加权组合，但是无法保证系统的稳定性，难以用数学模型准确表达。在虚拟结构方法中，将整组机器人视为刚体，可以保证编队形状的准确性，但不适合在群体规模增加的情况。在人工势场法中，利用势函数的梯度进行控制设计，通过选择一个合适的势函数，可以达到期望的整体行为，但由于该控制器有可能出现局部极小值问题，不能保证全局渐近收敛到目标编队。在领航跟随法中，跟随机器人需要跟随(虚拟)领队，同时保持领队所需的相对位置和方向，由于其易于实现，已被广泛研究以解决编队问题。

近年来，多机器人编队控制问题在自动驾驶，消防救援以及无人机编队等领域得到了广泛的研究，包括传统比例- 微分- 积分(proportion integration differentiation，PID)[12]，神经网络[13-14]、滑模控制（sliding mode control，SMC)[15]、模型预测控制(model predictive control，MPC)[16-17]、反步法(backstepping technique)[18-23]等。

为提高自动驾驶车队的纵向编队控制器的鲁棒性，文献[12]提出了一种车辆执行器时延和车车通信时延因素的纵向控制方法。同时推导出了车队纵向编队PID控制器参数的边界条件，并利用Lyapunov 稳定性理论，验证了车队保持队列的稳定性。CHU Zhongchu 等人[13]提出了一种自适应模糊神经网络控制方案，通过阻抗学习来协调具有未知动力学和时变约束的多个机器人。针对无人机飞行过程中存在的参数和外界扰动不确定性导致编队系统不稳定问题，曹志斌等人[14]设计了一种多四旋翼分布式神经自适应动态协同编队控制方法。采用学习维数低、实时性强的最小参数神经网络观测器，实现对四旋翼位置回路和角度回路未知非线性干扰的快速平滑学习与补偿。CHWA Dongkyoung 等人[15]使用SMC 算法的编队控制方法可以处理较大的初始跟踪误差，但其过程复杂且计算量大。张平等人[16]研究了自动驾驶汽车在高速公路上超车过程中的轨迹规划和跟踪控制，采用集中式模型预测控制器，实现了超车过程的轨迹跟踪。针对多移动机器人编队系统存在的干扰问题，LIU Andong 等人[17]提出了一种基于扩展状态观测器(extended state observer，ESO)的分布式模型预测控制(distributed model predictive control，DMPC)方法。

反步技术适用于非线性系统，成为常用的方法之一。该技术采用逆向设计思路，使得控制器设计更为直观和便捷，减轻了复杂的数学运算和系统建模的负担，从而进一步简化了控制器的设计过程。

为提高编队性能，文献[18]设计了基于反馈线性化的反步控制器。针对多四旋翼无人机的编队保持和防碰撞及机间通信问题，杨明月等人[19]设计了一种基于虚拟结构和人工势场相结合的编队规划控制算法，同时利用反步法实现无人机对期望轨迹的跟踪功能。针对四旋翼无人飞行器(unmanned aerial vehicle，UAV)模型参数不确定和外部干扰情况下的精确轨迹跟踪问题，文献[20]提出了一种自适应积分反步控制策略。同时，文献[21]利用基于反步控制技术解决了欠压自动潜航器三维轨迹跟踪中与运动参数跳跃相关的问题。此外，为解决欠驱动自主潜水器(autonomous underwater vehicle，AUV)模型参数中的不确定性问题，文献[22]提出了一种轨迹跟踪算法。该算法结合了径向基函数(radial basis function，RBF)神经网络算法和反步控制方法，采用状态预测策略，并通过仿真结果验证了该方法的有效性和鲁棒性。针对轮式移动机器人在运动学模型下轨迹跟踪误差较大的实际应用问题，文献[23]采用反步法设计了控制器，实现了对移动机器人位置误差和角度误差的精确控制。众所周知，基于反步法设计的控制器会因为初始误差的原因导致不现实的速度跳变超过其电机的最大限制，从而影响编队的控制性能。

为解决道路养护过程中交通锥摆放和回收的问题，本研究基于相对位置的编队控制，即选择一个或多个智慧锥作为领队，其余智慧交通锥为跟随者。针对智慧锥质心与中心(即智慧交通锥驱动轮轴线的中心)未在同一位置的情况下，构建智慧锥的误差动态方程。将微分同胚思想首次引入到反步设计中，并设计了一种新的映射函数，有效解决控制输入限制问题。借助MATLAB 和机器人操作系统(robot operating system，ROS)实验平台对该控制方法进行了数值仿真和实验验证，以验证该算法有效性和实用性。

1 工况背景与问题描述

1.1 摆放与回收工况

本文的应用场景为四车道高速公路封闭外侧车道的养护作业区域，如图1 所示。智慧交通锥编队工况由3 个阶段组成：第1 阶段，起始位置(应急车道)；第2阶段，进入编队摆放区；第3 阶段，编队回收工作(返回至应急车道)。其中，编队摆放由1 个警告区、2 个缓冲区、1 个工作区和1 个终止区组成。

图1 智慧交通锥初始位置和工况示意

根据《道路交通标志和标线》 (GB5768)的相关规定，摆放智慧交通锥的顺序应从警告区开始，逐步向终止区域推进。在回收时，顺序与摆放相反进行，其中，摆放的智慧交通锥之间的布设间距不宜大于10 m，警告区、上游过渡区和工作区的布设间距不宜大于4 m。在编队摆放之前，工作人员首先会将智慧交通锥从卡车上取下并移动至初始位置(应急车道)，具体操作通过遥控完成；然后，根据养护作业区域的要求，预先设置智慧交通锥的摆放标准位置；最后，当智慧交通锥接收到移动指令，便开始运动，直至到达警告区的摆放目标停止，即形成警告区的斜线编队。这里的警戒区是安全事故发生最频繁的位置，在本研究中作为主要摆放目标，其他区域则使用普通交通锥进行摆放。

1.2 微分同胚变换

对于给定的2 个微分流形H和J，微分流形之间存在可逆映射W:H→J，其逆映射表示为W-1:J→H。当映射W和W-1都是连续可微的，则映射W就被称为微分同胚。从其定义，可以看出微分同胚是将系统的状态方程从一个坐标空间转换为另一个坐标空间。

根据微分同胚理论，选在一系列Wi以满足：

其中：t∈R为时间，x∈Rn为系统的位置，λ为常数，Wi是微分同胚Xi上的一个局部微分同胚。针对fi(x,t)，提出以下映射函数：

其中：qi是转换前的变量。

将式（2）改写为

可知，当qi∈(-∞, +∞)，fi∈(-λ, +λ)；即fi(x,t)满足不等式约束。

1.3 智慧交通锥单机模型

如图2 所示，假设智慧交通锥在平面上运动，全局坐标系固定到笛卡尔空间，局部坐标系固连到智慧交通锥平台上。其中，Eoi表示第i个智慧交通锥的几何中心(i=1, 2, 3)，Eci表示第i个智慧交通锥的质心坐标。

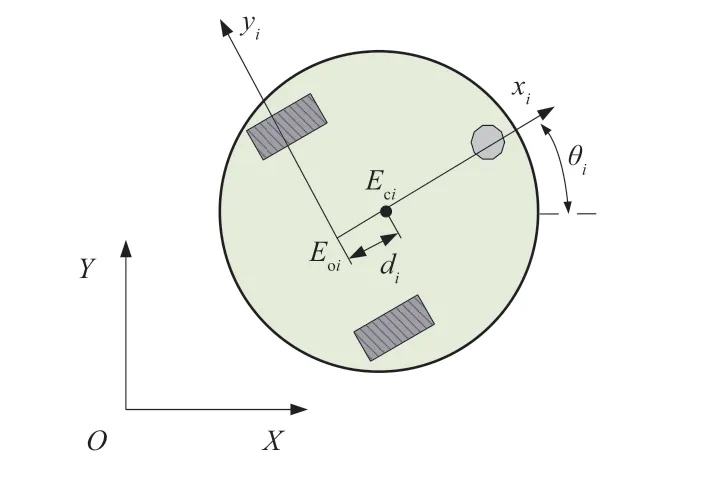
图2 智慧交通锥平面示意图

由于智慧交通锥的质心与几何中心不重合，可以得到Eo和Eci的关系，如下：

其中： (xi,yi) 为智慧交通锥的质心Eci的惯性坐标系OXY下的坐标位置；θi为方位角；(xoi,yoi)为智慧交通锥的几何中心在惯性坐标系OXY下的坐标位置；di表示Eoi与Eci之间的距离。

考虑智慧交通锥在纯滚动无滑动条件下运动，则运动学约束(非完整约束)为

根据运动学约束式(5)，可以得到智慧交通锥的运动学模型为

其中：vi和ωi分别表示智慧交通锥的线速度和角速度。

1.4 智慧交通锥编队模型

本文的智慧交通锥编队模型，其结构如图3 所示。

图3 智慧交通锥编队示意图

在全局坐标系下的跟踪误差定义[24]为：

其中：edx'i和edy'i分别为x方向和y方向的目标距离误差值。则本文的目标是对控制输入vi和ωi进行设计，以满足下面条件：

通过几何投影变换，可以得到全局和局部坐标系下的跟踪误差关系[25-26]。

结合方程（3）的结论，对式（11）求导可得

根据上述推导过程，可得到智慧交通锥系统的动态误差方程，

其中：vi-1和ωi-1分别为第i-1 个智慧交通锥的线速度和角速度。

2 基于微分同胚变换的反步法控制器设计

在本节中，由于在编队转弯时每个智慧交通锥的方位角不会一直保持一致，则在后面的控制器设计过程中忽略方位角的影响。将方程(14)改写为：

考虑镇定eyi，选择角速度ωi为：

根据式(19)，选择线速度为

可得

因此，系统是渐进稳定的。可得到本文的控制器如下：

其中：K1和K2是大于零的常数，vi和ωi不受限制，会因初始误差的原因超过其电机输入最大限制。

为了解决控制输入限制问题，结合电机本身的硬件要求，给出以下速度限制：

将变换(3)引入到控制输入限制中，则等式(22)改写为

若速度vi和wi∈ (-∞, +∞)，则u1i∈ (vmin,vmax)和u2i∈ (ωmin,ωmax)，符合实际要求。与直接对电机输入进行硬约束相比，采用微分同胚思想的方法可实现对控制输入的动态调整，使得系统响应更加平滑，避免了直接施加硬约束可能导致的过渡振荡和不稳定现象，有助于进一步提高控制系统的稳定性和控制性能。

3 数值仿真与实验

3.1 数值仿真

在本节中，通过MATLAB 数值仿真验证所提方法的优越性。考虑由3 个智慧锥所组成的编队系统，其通信拓扑结构如图4 所示。

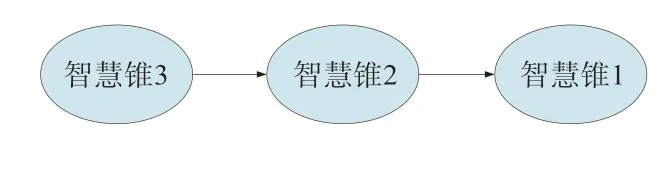
图4 控制器设计流程

从图4 中可以看出：智慧锥2 跟随智慧锥1 (领航者)，智慧锥3 跟随智慧锥2 (领航者)，以此类推，第i个智慧锥仅需要知道第i-1个智慧锥的位置信息，因此，根据不同工况的需求，可将智慧交通锥的编队扩展到更多数量的工况应用中。考虑2 种目标工况：

工况1：智慧锥从应急车道出发形成斜线编队并到达警告区，完成摆放任务。

工况2：在接收到回收命令时，智慧锥则需从摆放位置返回到紧急车道，结束编队任务(即，斜线队形变成直线队形)。

工况1：让智慧锥1 跟踪一个摆放目标(5, 0) m。

工况2：在工况1 的基础上，让智慧锥1 跟踪一个回收目标(10, 0) m。

其中：k1和k2是大于0 的常数。

初始位置分别设定如下：

工况1：x1= 0 m，y1= 0 m，θ1= 0°，x2= -1.1 m，y2= 0 m，θ2= 0°，x3= -1.9 m，y3= 0 m，θ3= 45°；

工况2：x1= 5 m，y1= 0 m，θ1= 0°，x2= 4 m，y2= -1 m，θ2= 0°，x3= 3 m，y3= -2 m，θ3= 0°。

给出智慧锥仿真参数，如表1 所示。图5 为智慧锥摆放工况的轨迹曲线图。由图5 可知：3 个智慧锥在本文所设计的控制器(式(25))作用下，依次从应急车道出发，保持相对稳定的目标编队到达摆放位置。

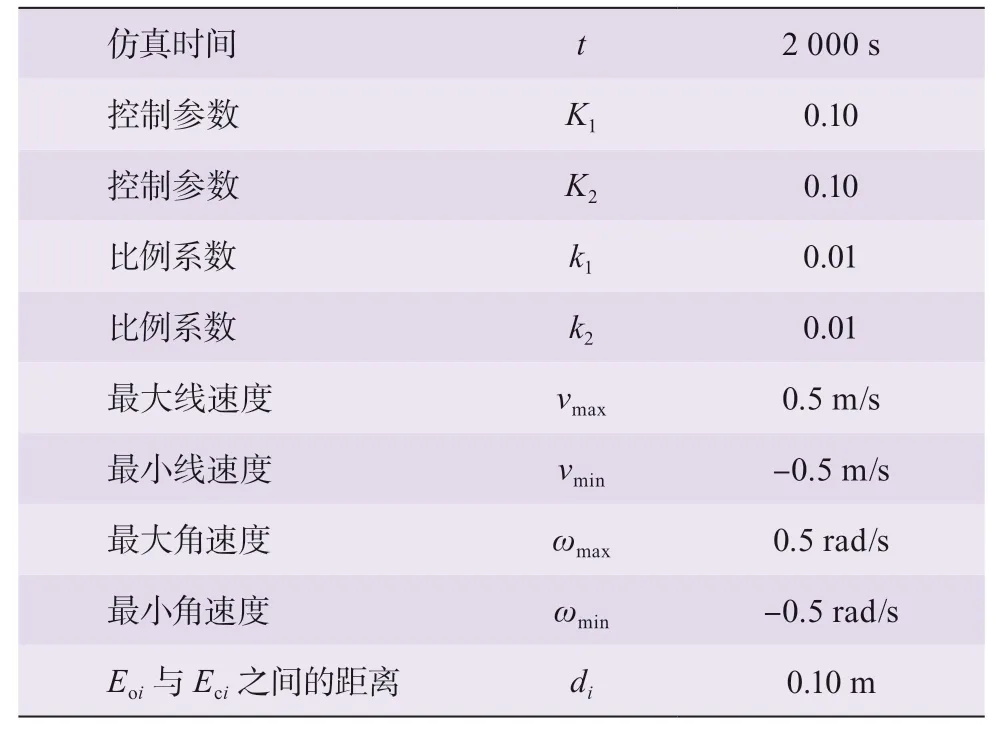
表1 智慧交通锥参数表

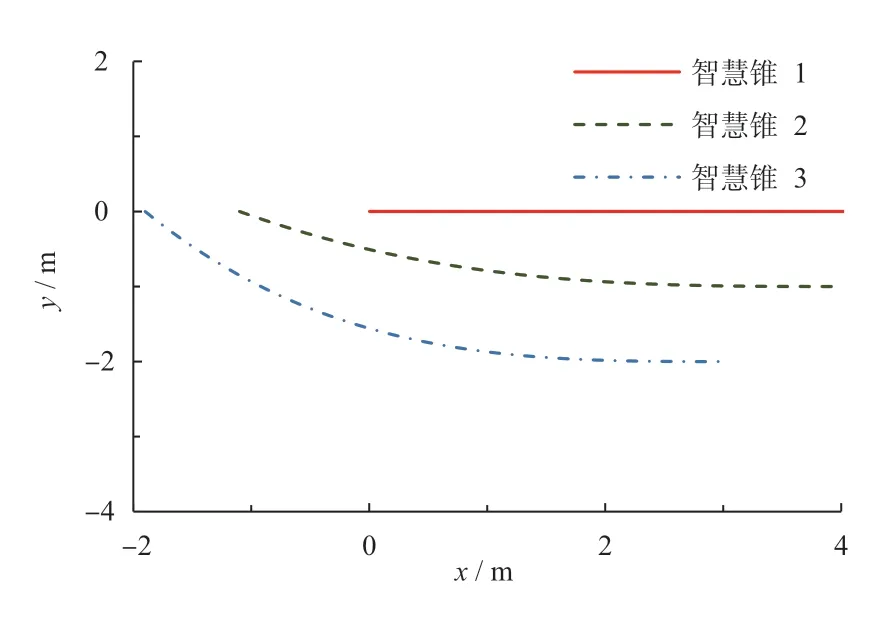
图5 智慧锥摆放工况轨迹

2 种工况仿真结果如图6-图12 所示。图6-图7为智慧锥摆放工况的速度、角速度曲线。图8 描述了3个智慧锥之间的距离随时间变化的曲线。

图6 智慧锥摆放工况线速度

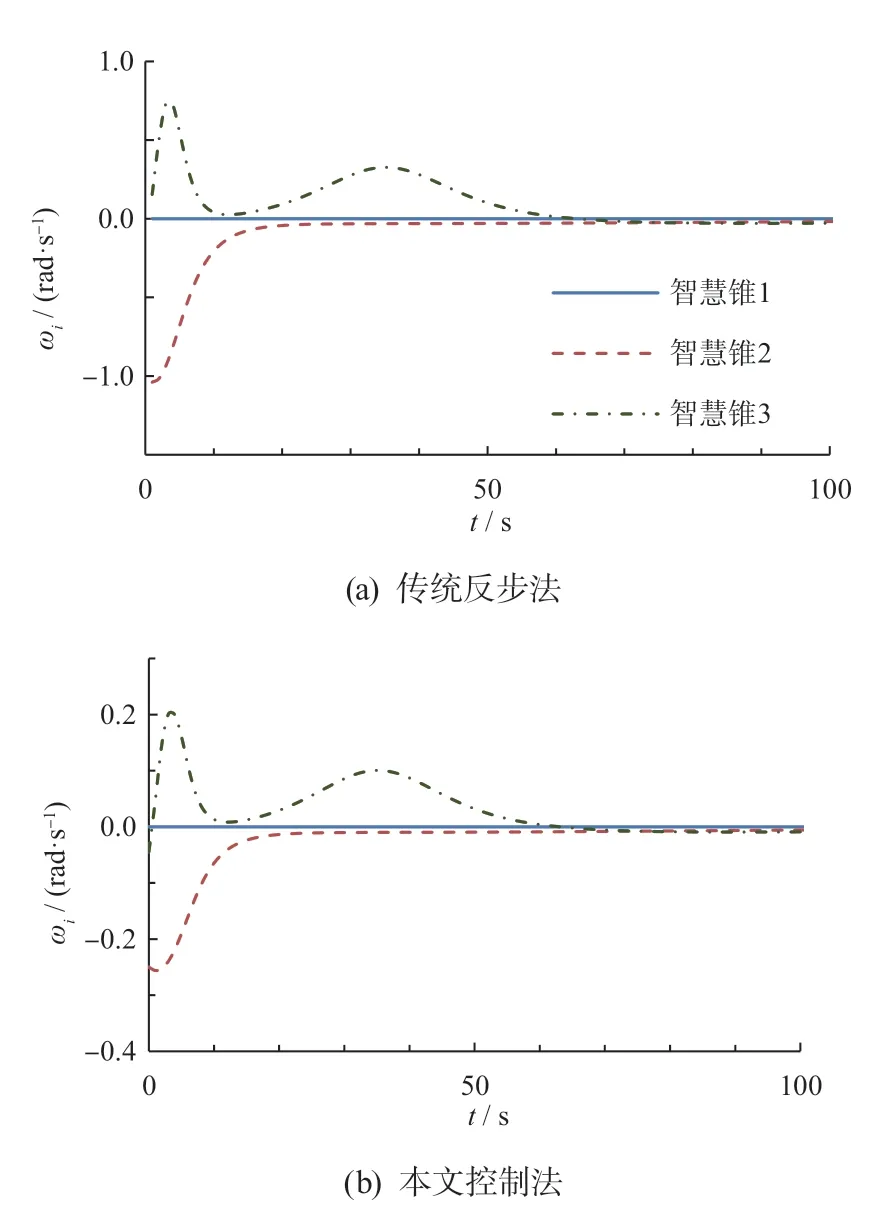
图7 智慧锥摆放工况角速度

图8 智慧锥摆放工况距离

由图7a 可知：由于初始位置误差的原因，角速度发生了明显的速度跳跃现象超过了其电机的最大值(ωi∈-0.5～0.5 rad/s)，这在实际应用中是不允许的。相比于传统的反步法，图7b 将微分同胚变换思想引入到编队设计中，可以将智慧锥的线速度和角速度控制在给定范围内，且变化平稳，这也体现了本文控制算法相比于传统算法的一个优势。由图8 可知：3 个智慧锥在x方向和y方向上的距离均在150 s 左右收敛于目标距离，即形成斜线的队形。

与工况1 一样， 图9-图11 分别为工况2 智慧锥的轨迹、速度、距离。

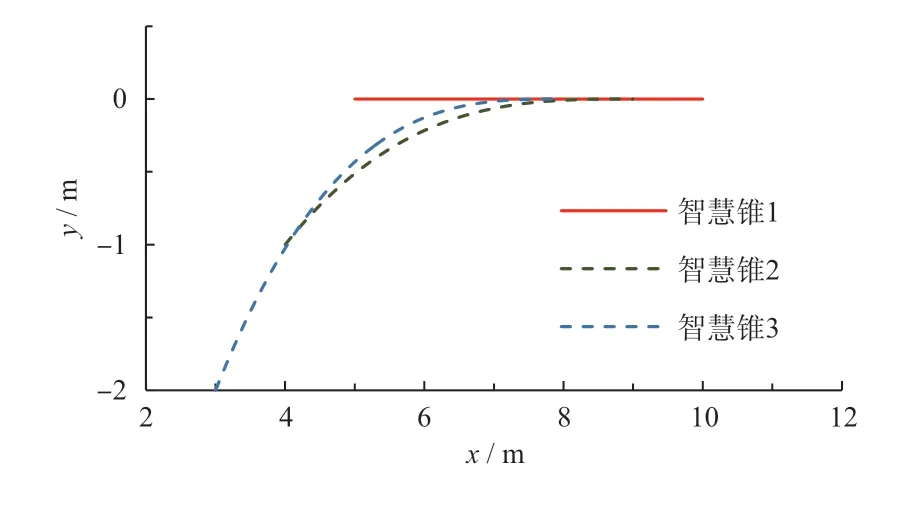
图9 智慧锥回收工况轨迹

从图10 可以看出：智慧锥在接收到回收指令后，依次从摆放位置返回至应急车道，整个过程依次有序，互不相交。从图11-图12 的结果可以看出智慧锥从警告区返回到应急车道位置的同时各个智慧锥之间的在x方向上的距离均收敛于期望距离1 m 和2 m，在y方向上均收敛于10 cm 以内。同时线速度、角速度分别收敛于0.1 m/s、0.1 rad/s 以内。综上所述,智慧锥系统在所设计的控制算法作用下，能够实现本文的工况要求，进一步验证了本文算法的有效性。

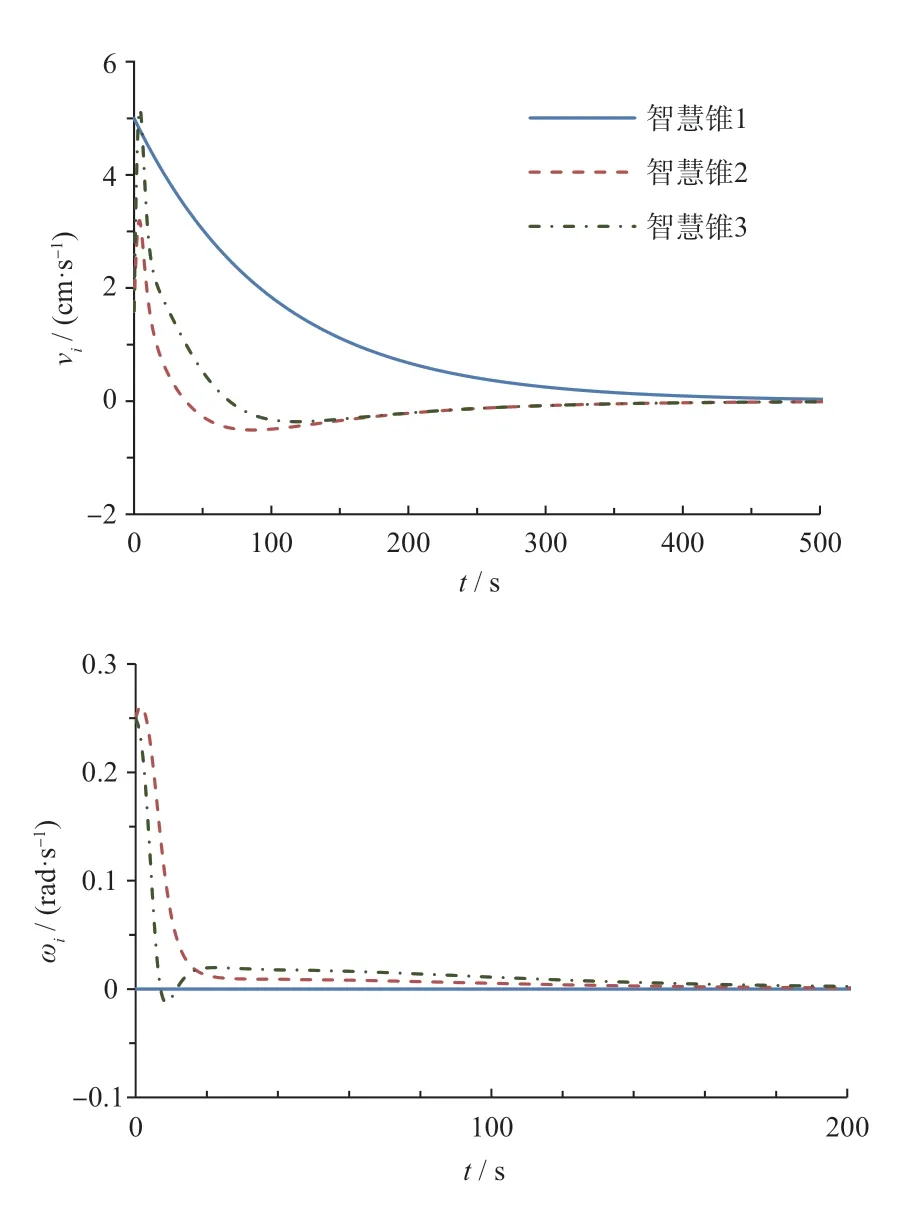
图10 智慧锥回收工况速度

图11 智慧锥回收工况距离

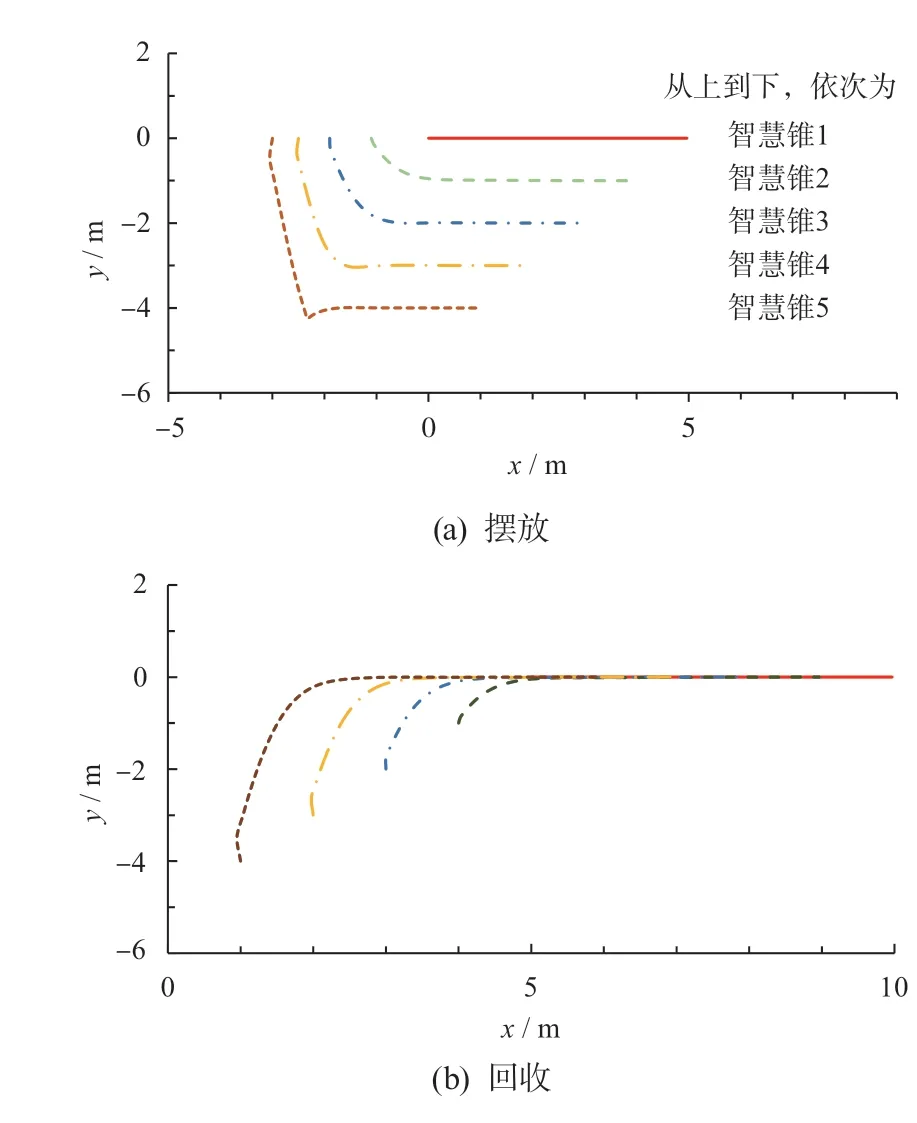
图12 5 台智慧锥摆放和回收工况轨迹

为了更好地体现算法在1.1 节中所述的典型场景的可拓展性，本文进一步补充了5 台智慧锥的仿真结果，如图12 所示。

从图12 可知：这5 台智慧锥的轨迹在任何时候都不会相交，并且在追踪摆放和回收固定目标的同时，保持了稳定的编队形态。实验结果表明，所设计的控制器对于更多的智慧锥仍然可行，具有良好的可拓展性。

3.2 ROS 实验与结果分析

采用3 台智慧交通锥进行实验。各智慧锥的初始参数与3.1 节相同。图13 为机器人实验平台框架图，包括移动机器人平台(Irobot)、控制器(Raspberry Pi)、传感器(Real-time kinematic(RTK) GPS)、电源和标准交通锥模型。上位机作为系统的监控层，通过WiFi 与树莓派进行交互。

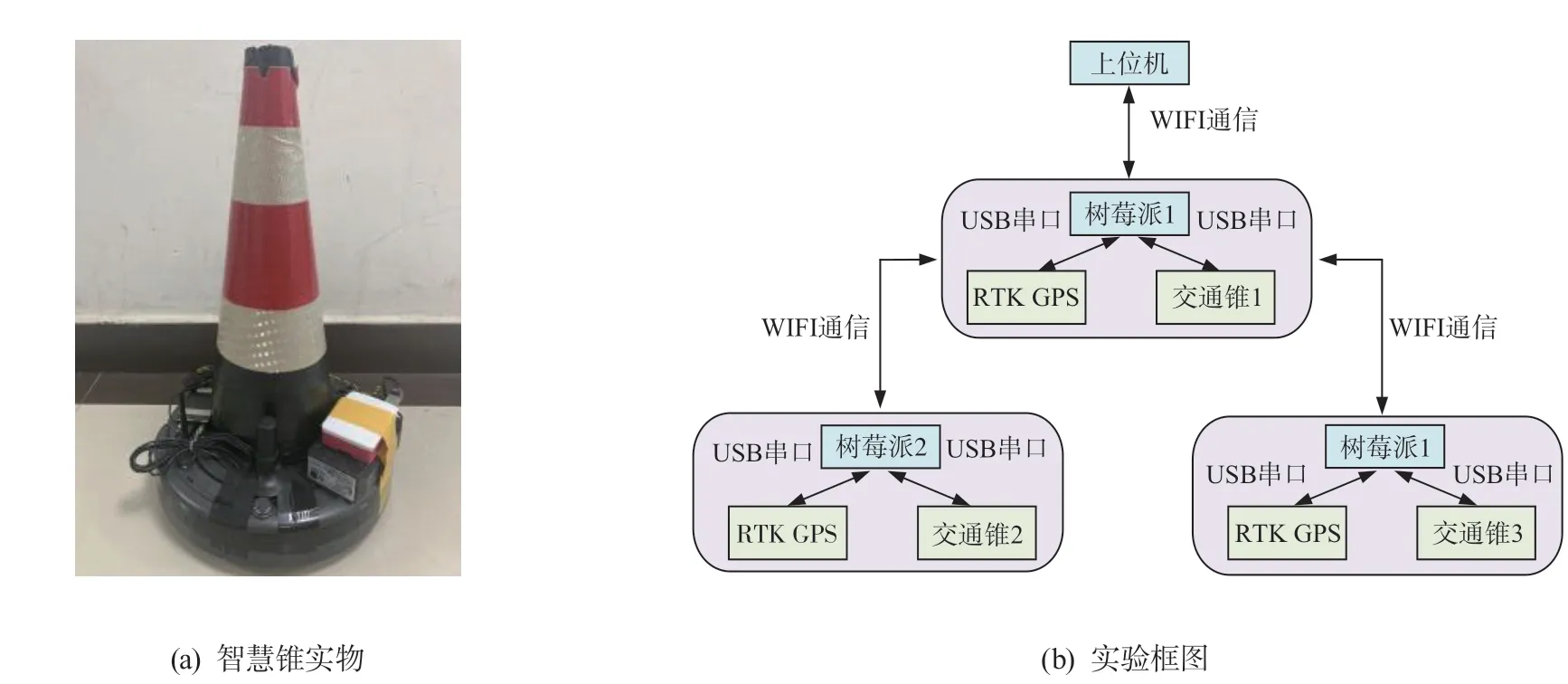
图13 智慧锥实验平台

树莓派通过USB(universal serial bus)串口与Irobot、RTK GPS(inertial measurement unit)传感器进行通信，其中，采用了RTK GPS 差分传感器来实时获取每台智慧交通锥的位置、航向和速度信息。同时，选择了KSXT 作为RTK GPS 报文的数据格式。根据KSXT报文信息，可以读取到智慧交通锥的经度、纬度信息以及方位角信息，然后根据经纬度信息，将智慧交通锥的位置转换到OXY平面坐标系中。在该坐标系中，原点的位置可以根据实际需求进行指定，其中X轴的正方向指向正东，Y轴的正方向指向正北。其具体的实验操作步骤如下：

1) 将树莓派与PC 机连接在同一局域网内，建立多机通讯网络。

2) 通过SSH 远程登陆服务，在PC 机上远程登陆树莓派，并启动各智慧交通锥。

3) 通过Launch 文件启动参数优化节点。

4) 启动RTK GPS 串口信息读取节点，并通过Launch 文件启动轨迹展示节点，将二者输出的经纬度、航向、速度等信息转换到OXY平面坐标系。

5) 启动智慧交通锥编队控制器。

6) 摆放(回收)作业完毕后，停止程序，保存智慧锥的轨迹信息。

本次实验在机器人操作系统(ROS)环境进行中，并利用Rosbag Record 命令进行编队数据记录，实验过程的控制参数与仿真参数保持一致。图14 分别给出了0、10、30、70 s 时摆放和回收工况下智慧锥的实验过程图。将数据进行可视化，如图15-图19 所示。

图14 智慧锥摆放工况实验场景

图15 智慧锥摆放和回收工况轨迹图

图15为智慧交通锥编队摆放和回收二维轨迹。图16为摆放工况下智慧交通锥之间的距离误差曲线。图17 为智慧锥速度曲线。与编队摆放工况一样，图18、图19分别为智慧交通锥的距离误差曲线图和速度曲线图。

图16 智慧锥摆放工况距离误差

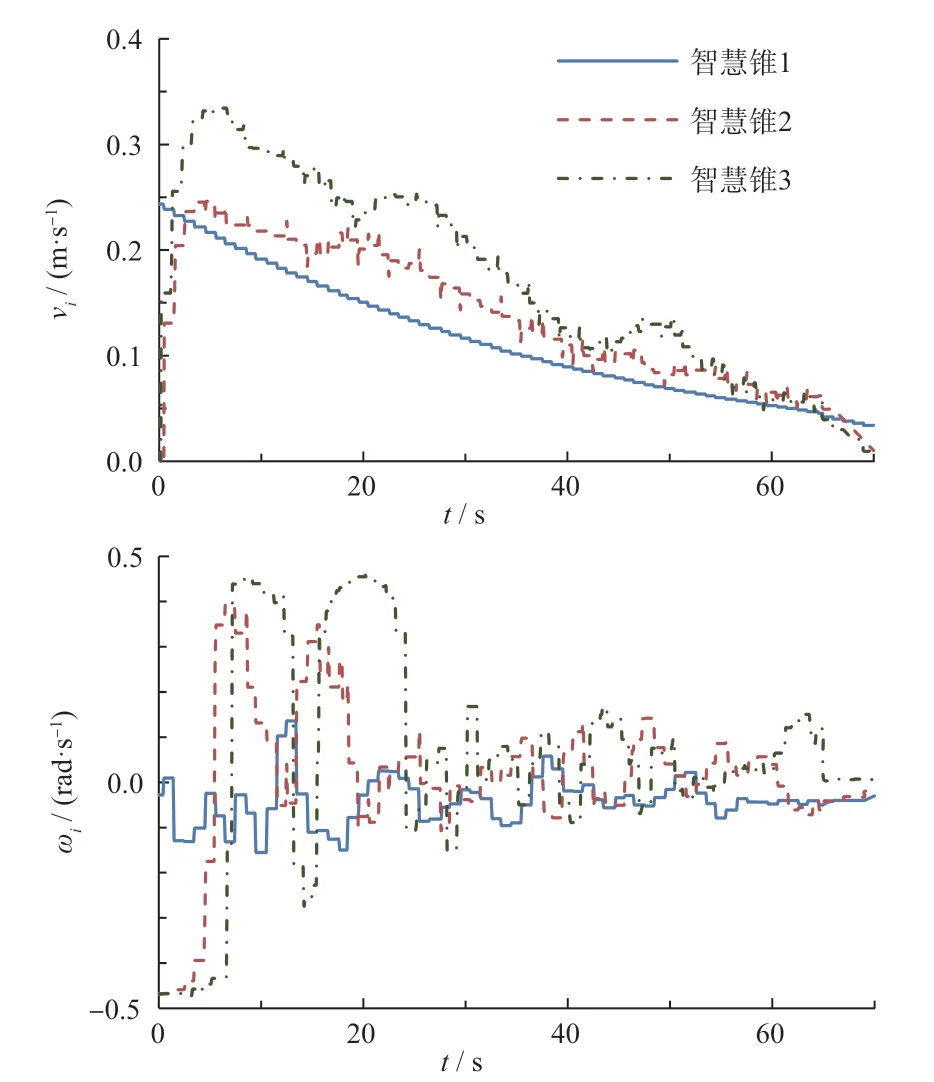
图17 智慧锥摆放工况速度、角速度

图18 智慧锥回收工况距离误差

图19 智慧锥回收工况速度

从图16 可知：所有跟随智慧锥的线速度和角速度均收敛于领航智慧锥的线速度和角速度。其中线速度和角速度均在电机所允许的范围内，即vi∈ (-0.5 m/s,+ 0.5 m/s)，ωi∈(-0.5 rad/s, + 0.5 rad/s)。

从图18 可知：由于外部环境的变化(例如：地面不平整、风速以及遮挡物等因素)，导致RTK GPS 传感器出现测量误差。这些误差导致智慧锥2 和智慧锥3之间的距离误差在40～60 s 之间突然增加。然而，在基于微分同胚变换的反步法控制器作用下，智慧锥能够在60 s 左右克服误差，使得彼此之间的距离误差ei均收敛到10 cm 左右。该结果表明控制器具有一定适应外部环境的能力。

由图19 可知：将基于微分同胚变换的反步控制算法运用在多智慧锥的回收控制中，速度均可以满足电机硬件需求，并收敛到期望队形返回至应急车道。

综上分析可知，实物实验结果与数值仿真结果一致，进一步验证了本文算法在实际场景中的可行性。

4 结 论

为了解决交通锥摆放和回收问题，本文将反步法设计理念应用至智慧交通锥动态误差方程中，阐述了该方法的设计原理与应用条件，并将单个智慧交通锥的轨迹跟踪问题拓展到了3 个智慧交通锥的编队控制问题中。根据系统的通信拓扑结构以及不同工况的需求，可将智慧交通锥的编队扩展到更多数量的工况应用中，具有较好的应用前景。此外，基于微分同胚变化的编队方法相比于传统的反步法，可以将智慧锥的线速度和角速度控制在给定范围内，且变化平稳。在所设计的控制算法作用下，整个智慧交通锥系统可保持目标编队到达摆放和前进回收位置。因此，该方法可为交通锥的摆放与回收问题提供一种新的控制方法。

考虑到智慧锥应用环境的复杂多变性以及对编队安全性能的高要求，在未来的研究中，如何在本文控制器的基础上消除环境中不确定性对系统稳定性的影响将成为一个重要的研究方向。