应用地基激光雷达三维点云数据构建长白落叶松树干削度方程1)
2024-01-12种雨丝何培张兹鹏姜立春
种雨丝 何培 张兹鹏 姜立春
(东北林业大学, 哈尔滨,150040)
立木材积的准确估计是森林有效管理和经营的重要环节之一。目前在国内外林业生产实践中,都使用削度方程估计立木材积和商品材积。通过伐倒木分段测量获取干形数据构建削度方程的方法耗时费力,具有破坏性,浪费木材资源[1]。随着测量技术的不断发展,采用非破坏性测量的地基激光雷达(TLS)技术获取干形数据[2-3],利用TLS技术调查森林资源,从确定单木位置、提取单木胸径和树高到预测树干直径、估算材积、监测森林的动态变化等获得高质量林木影像信息,提取林木丰富的水平和垂直信息[4-8]。
削度方程是以树木胸径、树高等单木特征因子作为自变量,以单木任意高度处直径作为因变量的函数[9]。削度方程在拟合时,通常使用非线性最小二乘法得到参数估计,该方法需要假定模型误差服从独立正态分布、非共线性和无自相关等[10],由于干形数据存在自相关性的问题,采用非线性回归需要消除自相关性,增加了模型参数估计的复杂程度。近年来,应用分位数回归和广义加性模型方法建立了树高-胸径模型、削度方程和枝下高模型等[11],由于分位数回归方法由多个分位点构建多个模型,灵活地反映林木数据的变化规律。广义加性模型以加性项组合的形式表达自变量与因变量之间的关系,在国内外林业生产研究领域得到广泛应用,并取得了较好的预测效果[12-14]。
长白落叶松(Larixolgensis)是我国东北林区的主要造林树种。以吉林省东丰县一面山林场和杨木林林场长白落叶松人工林为研究对象,使用TLS点云数据提取落叶松人工林单木干形数据。根据提取的数据,选取9个基础削度方程分别代表4种类型(简单、可变指数、三角函数和分段),利用非线性回归确定基础最优模型,构建分位数回归模型和广义加性模型,综合分析削度方程构建方法优劣,为落叶松干形精准预测提供技术支持。
1 研究方法
1.1 数据来源与处理
本研究落叶松干形数据采集地点为吉林省东丰县一面山林场和杨木林林场,地貌属于低山丘陵区,坡度平缓。该区域属于季风区中温带湿润气候,主要树种为落叶松、樟子松和红松等。于2021年7月在该区域内共选取了3块落叶松人工林样地,样地面积为0.04 hm2,样地内落叶松年龄为48~51 a,对样地进行每木检尺,测量胸径、树高、冠幅等单木特征因子。
TLS数据由FARO Focus 3D X 330扫描仪对样地进行扫描获得。依据各样地的坡度、郁闭度等环境因子调查情况,在各样地外围及内部分别布设5个站点,并在站点范围内设置5个靶球,保证每两个站点间可匹配到最少两对靶球,便于后期每个样地内不同站点的点云数据拼接。
用FARO SCENE软件完成同一样地不同站点之间的拼接处理,获得整个样地的点云数据,并以“.xyz”格式将点云数据导出。将FARO SCENE软件导出的数据(.xyz格式)加载到LiDAR360软件中,完成重采样、去噪、分离地面点,根据地面点归一化以及点云分割的数据预处理流程,获得样地和单木三维点云。对单木点云提取胸径、树高、冠幅以及相对树高(0、0.02、0.04、0.06、0.08、0.10、0.15、0.20、0.30、0.40、0.50、0.60、0.70、0.80、0.90)处的树木直径。
3块样地内共有落叶松75株,其中4株因树木冠层遮挡严重,提取树高与实际树高存在较大差距,因此本研究最终选用71株落叶松,共计1 065对树干相对高与直径干形数据。样木的胸径为12.8~28.4 cm,平均胸径为22.3 cm,标准差为4.2 cm;树高为16.4~24.5 m,平均树高为20.8 m,标准差为1.3 m。通过画散点图的方式剔除落叶松干形数据异常点(见图1)。
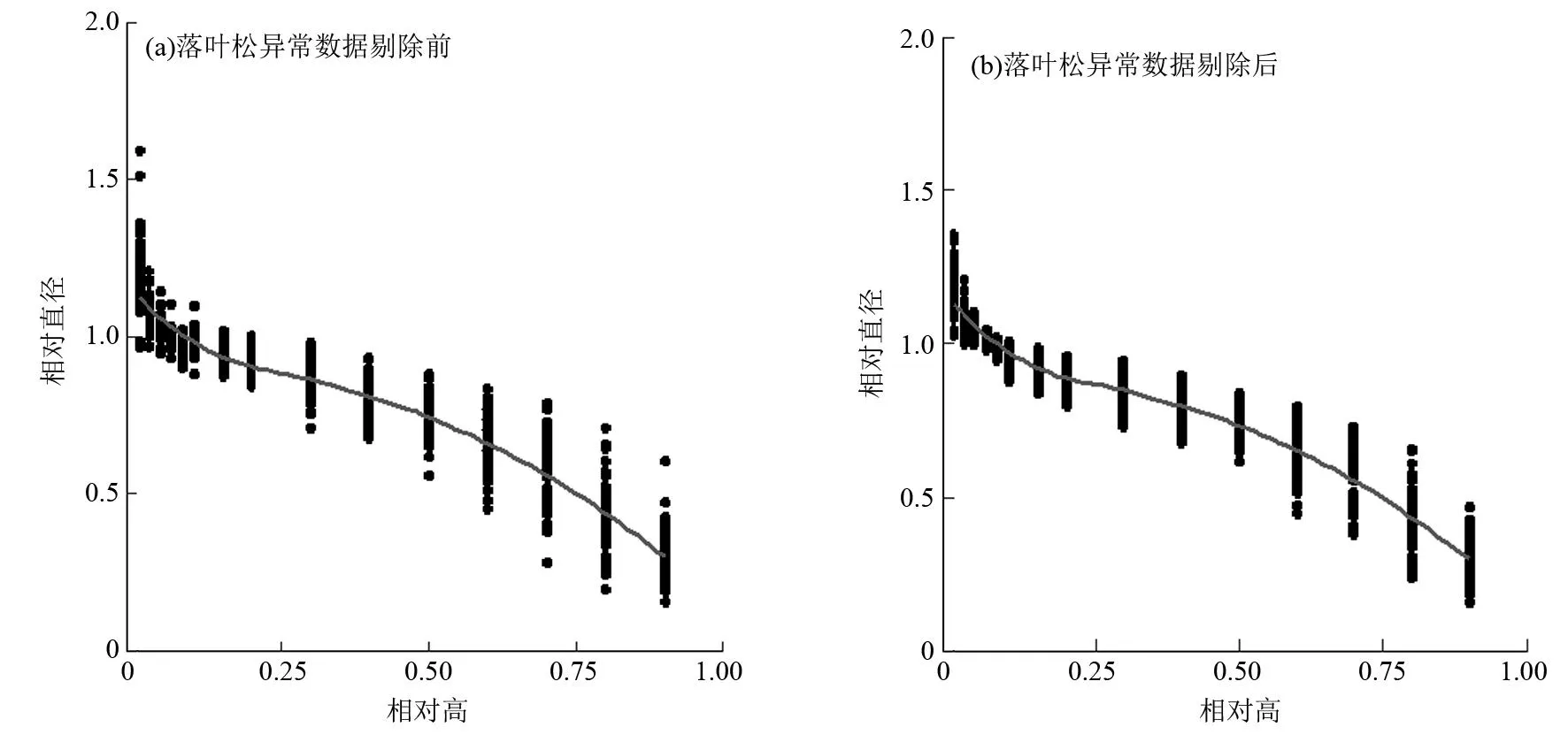
图1 数据处理前后相对高和相对直径散点图
1.2 基础削度方程选择
削度方程可大致分为简单模型、分段模型、三角函数和可变指数模型。简单模型通过使用基本初等函数模拟树干形状,模型容易构建,计算简便;分段模型借助拐点将树干划分不同的形状,相较于简单模型可提高干形预测精度;三角函数和可变指数模型则可通过变化的指数描述同一树干不同高度的树干干形变化[9]。本研究选用了Kozak(1969)、Lynch(2017)简单削度方程、Max-Burkhart(1976)分段削度方程(简称MB(1976))、Bi(2000)三角函数方程和5个可变指数削度方程作为本研究的基础方程[15-19],模型具体形式如下:
Kozak(1969)简单削度方程:
MB(1976)分段削度方程:
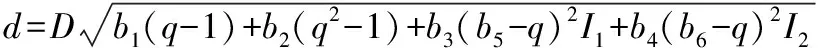
Kozak(1988)可变指数削度方程:
Kozak(1994)可变指数削度方程:
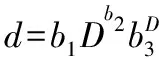
曾伟生(1997)可变指数削度方程:
Bi(2000)三角函数方程:
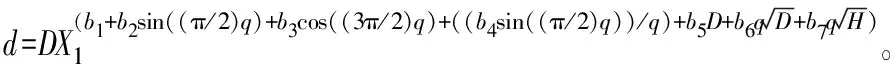
Kozak(2001)可变指数削度方程:
Kozak(2004)可变指数削度方程:
Lynch(2017)简单削度方程:
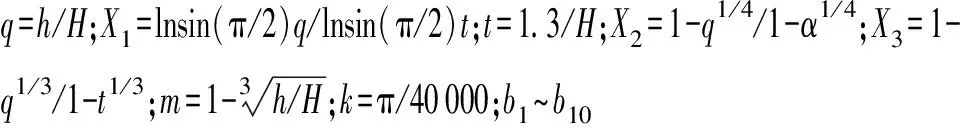
1.3 分位数回归
与传统回归法相比,分位数回归灵活性强,对数据分布没有要求。通过拟合任一分位点的数据,可估计不同分位点下的回归参数。主要研究不同分位点处自变量对因变量的变化趋势或研究不同分位点处哪些自变量是主要影响因素[20]。在树木干形预测方面,可以通过对比不同分位点回归模型对树干不同高度处直径的预测结果,分析不同分位点模型的干形预测精度。对分位数回归模型进行参数估计时,损失函数(Lmin)采用加权的最小二乘法,即通过最小化加权离差的绝对值之和获得方程参数。
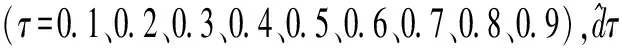
本研究采用quantreg包的nlrq()函数拟合各分位数模型。基础削度方程利用qnls()函数进行拟合,由于干形数据存在自相关特征,在基础削度方程拟合时引入CAR(l)函数来消除变量的自相关性[21]。
1.4 广义加性模型
广义加性模型是一种多元回归的非参数化平滑回归形式,用光滑函数代替线性函数,在建模之前不需要分析因变量与自变量之间的关系。广义加性模型由不同的光滑样条函数组成,模型中自变量和因变量之间可以为任意线性或非线性的关系,引入的光滑样条函数可增加对因变量预测的准确性,灵活地探测数据间的复杂关系,解释因变量随自变量变化规律。构建削度广义加性模型,可选取树干直径或树干相对直径作为因变量,选取胸径、树高和相对树高作为自变量,同时对自变量进行平方、根号等变换。广义加削度模型如下:
式中:dij表示第i株树第j位置处的直径;Di表示第i株树的胸径;dij/Di表示第i株树的相对直径;Hi表示第i株树的树高;hij表示第i株树第j位置处的高度;hij/Hi表示第i株树的相对高度;i=1、2、3、…、n,j=1、2、3、…、n。α表示截距;f(·)表示不同的光滑样条函数。
利用R软件mgcv包的gamm()函数对广义加模型进行拟合,对不同的加性项选择三次回归样条函数(CR)、B-样条函数(BS)、薄板回归样条函数(TP)、P-样条函数(PS)、Duchon样条函数(DS)和高斯过程平滑样条函数(GP)。
1.5 模型评价和检验的方法
模型评价指标包括确定系数(R2)、平均绝对误差(MAE)、相对误差(MPB)、均方根误差(RMSE)和多重共线性指标条件数(CN)。当CN<30时,模型自变量不存在多重共线性;当30

模型检验采用留一交叉验证法进行验证。该方法每次只选择一个样本数据作为验证数据,其余数据作为拟合数据,依此循环,直至每个样本数据都被作为一次验证数据结束,拟合和验证的次数等于样本数。
1.6 模型相对排序值的计算方法
当多个模型的评价指标不统一时,使用相对排序法计算各模型的相对排序值[23],计算方法如下:
式中:Ri为模型i的相对排序值(i=1、2、…、a),Ri值越小表示该模型的预测效果越好;a为参与排序的模型数;Si为模型i的评价指标值;Sx和Sn分别为Si的最大值和最小值。
在此排序方法中,最优模型排序值为1,最差模型的排序值为a,其余模型排序值为1~a。确定系数(R2)值越大,表示模型的拟合度越好,而平均绝对误差(MAE)、相对误差(MPB)和均方根误差(RMSE)越小模型精度越高。计算确定系数(R2)的相对排序值时,Sx和Sn分别表示R2的最小值和最大值。最终以确定系数(R2)、平均绝对误差(MAE)、相对误差(MPB)、均方根误差(RMSE)等4个指标的平均值作为该模型的相对排序值,排序值最小的模型即为最优模型。
2 结果与分析
2.1 基础模型的拟合结果
基于TLS落叶松提取的干形数据,利用R软件拟合9个基础削度方程,在拟合过程中,若模型中存在不显著的参数(P>0.05),就删除不显著参数后再次拟合,直至模型中所有参数显著。
由表1可知,MB(1976)模型的参数估计值(b5和b6)表明了影响落叶松干形变化的两个拐点分别位于相对高度0.73和0.07处。
由表2可知,Bi(2000)模型的拟合效果最好,其次是Kozak(1988)和Kozak(2004)模型,而Kozak(1969)模型的拟合效果相对较差。MB(1976)、Kozak(1988)、Kozak(1994)、曾伟生(1997)和Lynch(2017)模型的多重共线性指标条件数(CN)大于100,说明各模型自变量存在严重的多重共线性;Bi(2000)、Kozak(2001)和Kozak(2004)模型的CN值为30~100,各模型自变量多重共线性在可接受范围内;Kozak(1969)模型的CN值小于30,模型自变量不存在共线性。因此,基础削度方程中Bi(2000)模型的拟合效果最好,CN值也在可接受范围内。
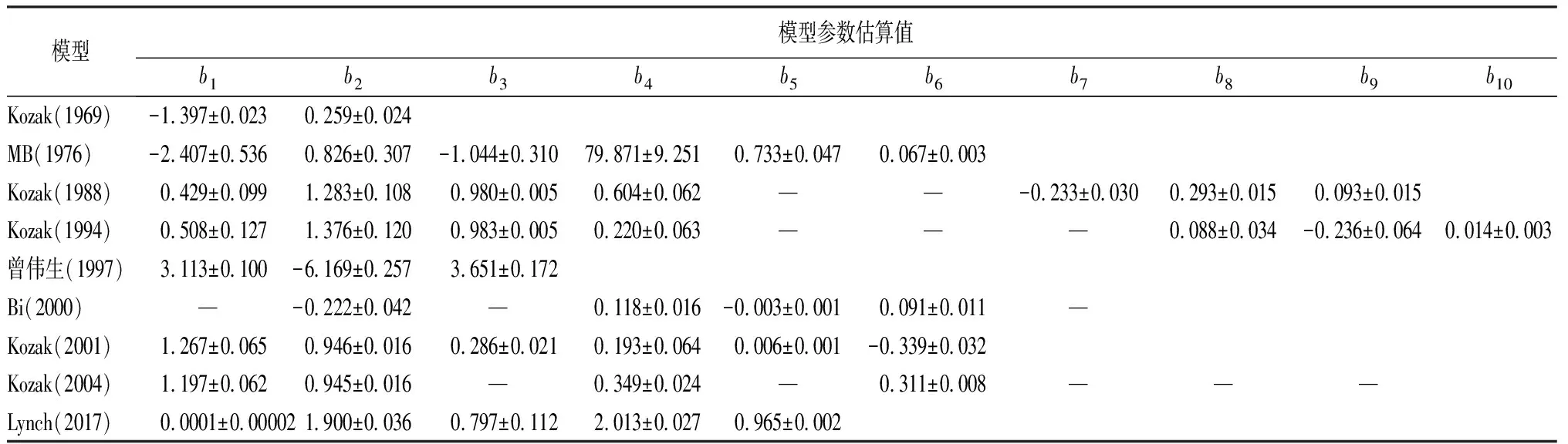
表1 落叶松削度方程的参数估计值
2.2 分位数模型的预测结果
根据拟合精度最高的Bi(2000)模型,构建9个分位数(τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9)削度方程形式如下:
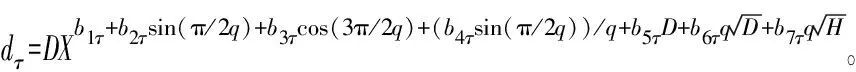
式中:dτ为各分位点处的直径,b1τ~b7τ为模型参数。
通过对分位数模型的9个分位点的拟合,9个分位点中,分位数τ=0.4、0.5、0.6分位点处的拟合精度较高。
由表3可知,不同分位点下模型的参数估计值均不相同,说明在不同分位点下,落叶松干形的拟合结果存在一定的差异。随着分位点数的增加,分位数模型的平均绝对误差、相对误差、均方根误差值呈现先减小后增加的特征,确定系数(R2)呈现先增加后减小的特征,在分位点τ=0.5处,模型拟合效果最好(平均绝对误差为0.847、相对误差为4.510、均方根误差为1.211、确定系数(R2)为0.963),且与非线性回归拟合效果基本相近。
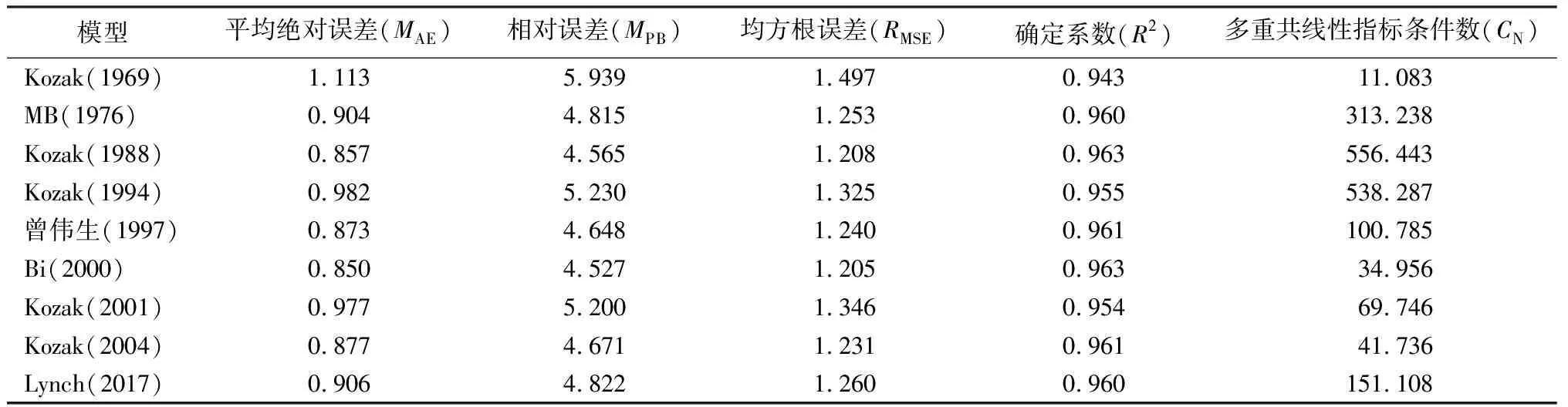
表2 落叶松削度模型拟合效果

表3 落叶松分位数回归模型参数估计值及拟合效果
2.3 广义加性模型的预测结果
对广义加性模型中的非参数平滑项f(·),使用6种样条函数(TP、CR、BS、PS、DS和GP)拟合。经对比分析各模型的拟合统计量,当不同加性项使用同一样条函数时,6个样条函数中,CR、TP和DS样条函数的拟合效果较好,分别记作模型1、模型2和模型3。
根据拟合精度最高的DS模型(模型3),胸径和树高所在加性项依然使用DS样条函数,相对树高所在加性项依次使用其余5个样条函数(TP、CR、BS、PS和GP)重新进行拟合。经比较分析,DS样条函数分别与CR、TP和GP样条函数组合后的模型拟合效果较好,分别记作模型4、模型5和模型6。
由表4可知,模型4的拟合精度优于模型1、模型3;模型5的拟合精度高于模型2,与模型3的拟合精度基本相同;模型6与模型3的拟合精度相同。各模型的拟合效果从高到低可排序为:模型4、模型5、模型3(模型6)、模型2、模型1。

表4 落叶松非参数模型拟合效果
2.4 模型预测精度的检验
根据3种建模方法(基础模型、分位数模型和广义加性模型)取得的最优模型,使用留一交叉验证法对Bi(2000)非线性模型、Bi(2000)分位数模型和广义加性模型进行检验。
由表5可知,根据分位数回归构建的Bi(2000)模型的预测精度略高于传统非线性回归模型,广义加性模型的平均绝对误差、相对误差、均方根误差、排序值均为最小,确定系数(R2)为最大,预测精度最高。
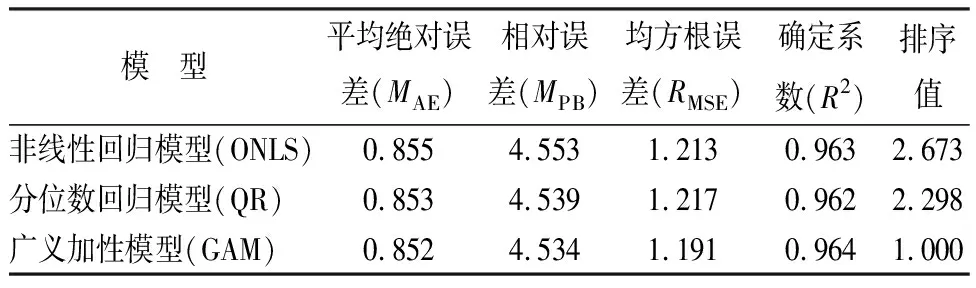
表5 落叶松削度方程检验结果
为进一步比较各模型(ONLS、QR和GAM)在树干不同高度处的预测能力,计算了各模型在9个相对树高处的平均绝对误差和均方根误差值。
由图2可知,根据平均绝对误差和均方根误差值随相对树高的变化情况,非线性回归模型和分位数回归模型在不同相对树高处的预测精度基本一致。在树干相对树高10%以下,广义加性模型的平均绝对误差值略大于非线性回归模型和分位数回归模型,均方根误差值与非线性回归模型和分位数回归模型基本相同;在相对树高10%~80%范围内,广义加性模型的平均绝对误差和均方根误差值均小于非线性回归模型和分位数回归模型;在相对树高80%~90%处,广义加性模型的平均绝对误差值处于非线性回归模型和分位数回归模型之间,均方根误差值小于非线性回归模型和分位数回归模型。因此,广义加性模型在树干大部分的预测精度都优于非线性回归模型和分位数回归模型。
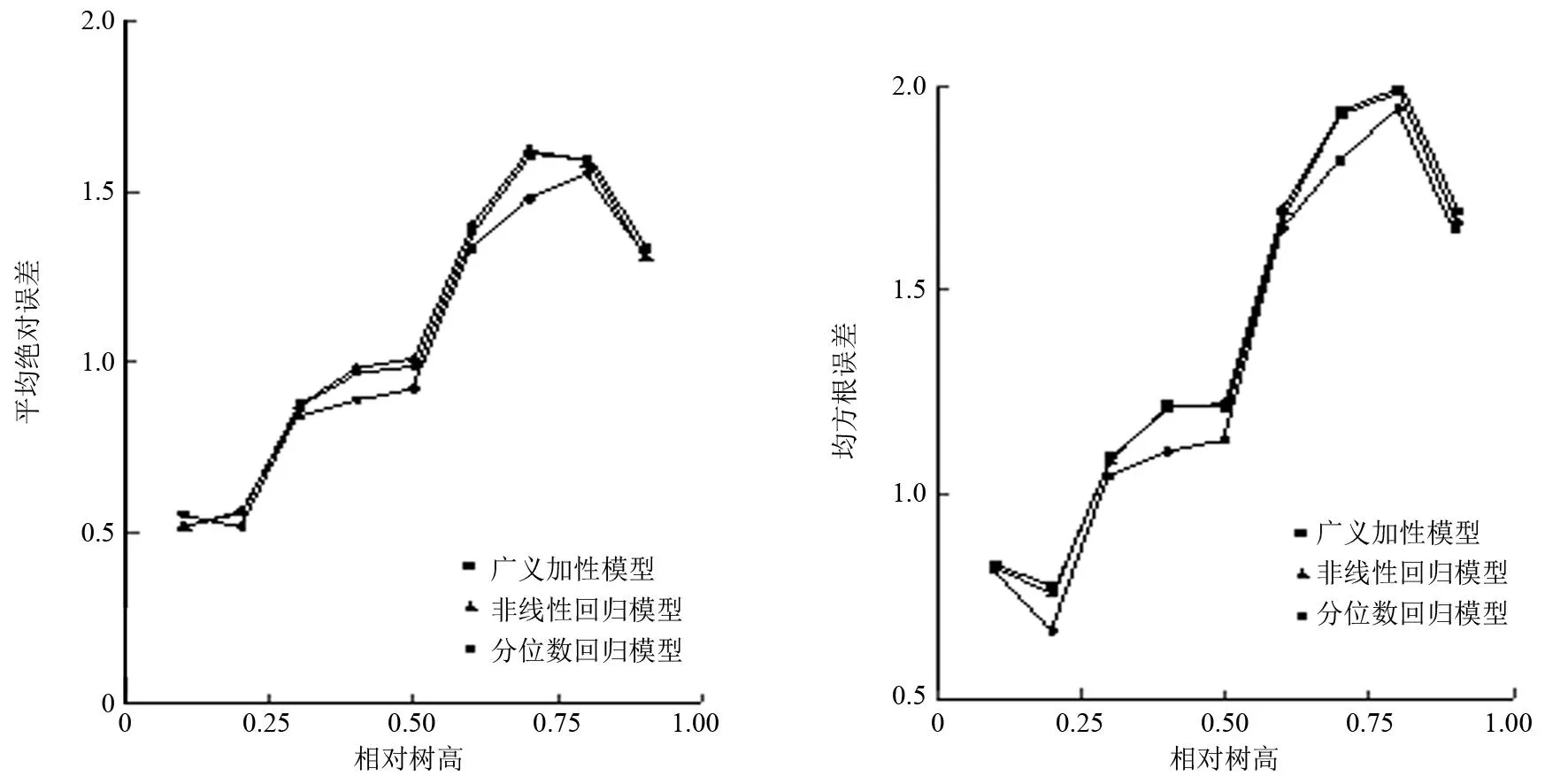
图2 落叶松削度方程在树干不同高度处的预测能力
3 讨论
选取了9个基础削度方程进行比较,这些方程分别代表简单、分段、三角函数和可变指数削度方程等4种类型。可变指数Bi(2000)模型的拟合效果最好,除Kozak(1969)模型外,其余7个模型的拟合统计量比较接近。但研究发现Kozak(1988)模型存在比较严重的多重共线性问题。邹茂胜等[24]研究认为Kozak(1988)模型优于Kozak(2004)模型和曾伟生(1997)模型。

在最优基础模型的基础上构建了9个分位点(τ=0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9)的分位数回归模型。中位数(τ=0.5)模型的拟合效果最好。通过比较2个模型的预测精度发现非线性模型和中位数模型都可以较好的描述干形变化,但中位数回归模型没有假设要求,建议使用分位数回归模型。但两个参数模型在树干大部分范围内的预测精度都略低于广义加性模型,因此,3种建模方法中,推荐使用广义加性模型预测树干直径。
地基激光雷达技术作为干形数据获取的一种手段,由于受林分密度和枝条生长状况等因素的影响,该技术也存在一定的局限性。对树冠体积较大的单木,在树干相对高80%以上,树干直径信息量低于中下部,需手动提取树干直径,提取精度相对较低,会对干形预测精度有影响。在设置多站点扫描的情况下,可通过多数据源融合的方法补充树干上部点云信息,提高树干直径提取精度,进而提高干形预测精度。
4 结论
本研究基于地基激光雷达技术获得了落叶松人工林样地的三维点云信息,提取了落叶松的树高、胸径和不同相对树高处的树干直径等单木信息,并对比分析了传统削度方程、分位数回归削度方程和广义加性削度方程的预测精度。广义加性模型的预测精度优于传统削度模型和分位数回归模型,其中以相对直径为因变量,以胸径的平方、树高和相对树高的平方根为自变量,使用组合样条函数的广义加性削度方程更适合描述该区域的落叶松干形变化。
