仿生树状分形薄壁结构的耐撞性研究

2024-01-12吴斌李伟伟张继鹏王玥

山东理工大学学报（自然科学版） 2024年2期

吴斌，李伟伟，张继鹏，王玥

(山东理工大学交通与车辆工程学院，山东淄博 255049)

随着汽车数量的增加,交通安全事故的发生率也越来越高,严重威胁着乘员的生命。因此,有必要对汽车的被动安全进行研究,以减少事故对乘员的伤害。为了提高汽车被动安全的耐撞性,最常用的方法之一是在汽车前部安装吸能装置。薄壁结构由于其质量轻、制造成本低、吸能效率高等优点,在航空航天、交通运输、民用和军事设施等许多领域被广泛用作能量吸收器[1]。其通过自身的压溃变形来缓冲吸能,从而达到保护乘员生命安全的作用。

近几十年来,国内外研究人员通过理论、数值和实验等不同方法对不同截面形状薄壁管的耐撞性进行了研究。1960年,Alexander[2]提出了金属薄壁结构轴向压溃变形的理论模型。Abramowicz等[3]深入研究了薄壁结构折叠角的变形原理,提出了超折叠单元模型,建立了其平均冲击力的理论预测公式。Abramowicz[4]对理论进行了扩展,进一步提出了有效压缩距离的概念。Chen等[5]提出了一种基于薄膜变形能和弯曲变形能的简化超折叠单元理论。徐少强[6]在超折叠单元理论的基础上,推导了多胞薄壁管的平均冲击力理论预测公式。

经过亿万年的进化和自然选择,生物早已具备了巧妙的结构和出色的性能来应对外界的极端环境。通过将材料布置在合适的位置,生物结构可以最少的材料成本来实现所需要的功能,这也为工程结构设计提供了重要的灵感来源。近年来,通过仿生学来设计能量吸收结构成为研究的热点。牛枞等[7]以雀尾螳螂虾螯为仿生原型,结合仿生学设计方法,设计了一种含正弦胞元的多胞薄壁管结构,在不同加载角度下进行了耐撞性分析。黄晗等[8]基于虾螯的微观结构,提出了一种含人字形的多胞薄壁管,并采用响应面法进行了结构优化。Xu等[9]以蜘蛛网结构作为仿生原型,设计并研究了具有层级自相似特性的薄壁管。基于樟子松的自相似层次结构特性,徐少强等[10-11]设计了角自相似和多边接头自相似两类层次自相似多胞薄壁结构,推导了薄壁结构的平均冲击力理论公式,分析了其耐撞性能并进行了优化。

本文以树状分形结构为灵感,结合当前薄壁管的研究提出了两种新颖的多胞薄壁结构,并结合理论分析和有限元仿真技术对薄壁管的耐撞性能进行了研究。

1 仿生树状分形薄壁管

1.1 仿生原理分析

受自然界树枝的分形启发,本文提出了两种仿生树状分形设计,其简化的分形过程如图1所示。

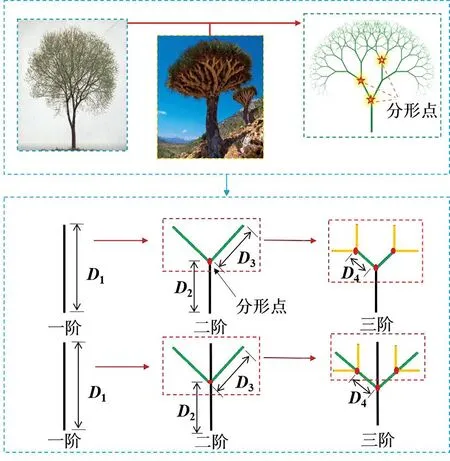
图1 树状分形图

第一种分形过程是在具有分形点的一阶结构开始,然后在分形点形成两个分支子结构以获得二阶分形结构;接着,在每个新的分支上设定一个新的分形点,再形成两个分支以获得三阶分形结构;重复以上过程就可以得到更高阶数的结构。第二种分形过程与第一种分形过程类似,但在分支过程中保留了上阶的原始结构。本文只考虑了两类分形过程形成的前三阶分形结构。

本文选取系数δ表示分形点的位置,公式表示为

(1)

式中：D1和D2分别表示一阶分形前后的结构长度,D3和D4分别表示二阶分形前后的分支长度。

1.2 仿生结构设计

本文依据上述分形设计,提出了两类基于传统方管的仿生设计。选择图2中所示的多胞薄壁管来执行树状分形设计,基于图1中的两类树状分形过程,提出了基于正方形截面的两类仿生多胞薄壁管。为方便起见,本文用图2中的英文标识来表示各个薄壁管。其中,缩写TFS(tree-liked fractal structure)表示树状分形结构,字母A和B分别表示第一类和第二类分形,数字1、2、3表示相应的阶数。同时,采用方形单胞管(SQUARE)作为基础结构进行对比研究。考虑实际的加工难度和成本控制,本文只扩展到三阶结构。

图2 TFS的横截面演变图

1.3 耐撞性评估

为了研究结构的耐撞性,选用以下5个评价指标：

1)能量吸收EA(energy absorption)表示碰撞过程中吸收的能量,即力对碰撞过程中位移的积分,表达式为

(2)

式中：d为有效压缩距离,x为碰撞距离,f(x)为冲击力。

2)比吸能SEA(specify energy absorption)表示单位质量的薄壁管吸收的能量,表达式为

(3)

式中m为薄壁管的总质量。

3)峰值冲击力Fp(peak crush force)为碰撞过程中瞬时的最大冲击力。

4)平均冲击力Fm(mean crush force)定义为吸收的能量总和与有效压缩距离的比值,表达式为

(4)

5)载荷效率CFE(crush force efficiency)用来描述变形过程中冲击力的稳定性,表达式为

(5)

当CFE值越接近于1时,峰值冲击力和平均冲击力之间的偏差越小,能量吸收过程中的效率越高。理想的吸能结构CFE值为1。

2 平均冲击力理论模型

理论分析预测是一种直接估计薄壁结构耗散能量的简便方法,精度高,计算成本低。因此,本文应用简化超折叠单元理论模型[12]来预测所提出仿生结构的平均冲击力。

在简化的超折叠理论中,假设每个折叠波长(2H)在多胞管的压缩过程中是恒定的。根据管内系统的能量平衡,压缩过程中的外功通过弯曲和薄膜的塑性变形消散,表达式为

Fm×2Hk=Eb+Em,

(6)

式中：k为有效压缩距离系数,Eb和Em分别为弯曲变形能和薄膜变形能。有效压缩系数k的引入是因为面板在压缩过程中没有完全压平,导致折叠的实际长度小于2H。根据研究,k的取值在0.7和0.8之间[13]。在本文理论模型中,k取值为0.7。

如图3所示,当面板折叠时,折叠的弯曲变形被简化为3个水平塑性铰线。假设发生完整折叠,即两条塑性铰线旋转90°,一条塑性铰线旋转180°。因此,弯曲能量耗散的表达式为

Eb=2πM0Lc,

(7)

式中：Lc是截面的总长度;M0=σ0t2/4为完全塑性弯矩,t表示薄壁管的壁厚,σ0表示材料塑性流动应力,可由下式计算得到

(8)

式中：σy为材料的屈服应力,σu为材料的极限应力,n是材料的应变硬化指数。

图3 弯曲塑性铰线

薄膜变形能取决于角单元的形状,是所有角单元的塑性折叠能量耗散的总和。图4显示了仿生薄壁管不同角元素的分布,可以分为三类,即二面板(2-panel)、三面板(3-panel)和四面板(4-panel)角单元。在一个折叠波长2H内2-panel能量耗散可以计算为[12]

(9)

(a)SQUARE (b)TFS-1 (c)TFS-A2

(d)TFS-A3 (e)TFS-B2 (f)TFS-B3图4 角元素示意图

根据三面板角单元的几何特征,又可分为四类：3-panel-1、3-panel-2、3-panel-3和3-panel-4。对于3-panel-1角单元,薄膜变形能计算公式为[12]

(10)

式中θ1如图4(b)所示,其值为45°,则

(11)

对于3-panel-2角单元,薄膜变形能计算公式与3-panel-1角单元相同,只有角度值不同,为90°,则

(12)

对于3-panel-3角单元,薄膜变形能计算公式为[12]

(13)

式中θ2如图4(c)所示,其值为90°,所以薄膜变形能为

(14)

对于3-panel-4角单元,薄膜变形能计算公式为[12]

(15)

式中θ3如图4(d)所示,其值为45°,所以薄膜变形能为

(16)

根据四面板角单元的几何特征,又可分为两类：4-panel-1和4-panel-2。对于4-panel-1,其薄膜变形为[14]

(17)

对于4-panel-2角单元,可以认为是一个3-panel-3角单元和一个附加面板单元合并而成。附加面板单元的薄膜变形能为[14]

(18)

式中θ4如图4(f)所示,其值为45°,则

(19)

多胞薄壁管的薄膜变形能由以上角单元组合得到,即

(20)

代入各角单元的薄膜变形能,得

(21)

式中：

(22)

将式(7)和式(21)代入式(6),得

(23)

在压溃的过程中,当薄壁管在最小的压溃载荷下发生理想变形时,利用稳态条件：

(24)

可得折叠半波长为

(25)

将式(25)代入式(23),可得平均冲击力的预测公式为

(26)

式(26)是在准静态轴向压缩的工况下得到的。为了得到在动态负载下的理论公式,需要引入动态系数λ。根据Langseth等[15]的研究,动态系数通常取1.3～1.6,本文选取λ=1.3。因此,仿生薄壁管在动载荷下的平均冲击力可表示为

(27)

各阶多胞薄壁管的各类角元素数量见表1,将角元素的数量代入式(27),可得到各个薄壁管平均冲击力的理论公式。

3 有限元数值模拟

3.1 有限元模型

根据图2所示的横截面几何特征,在HyperMesh中建立了两类薄壁结构的网格模型,并在LS-DYNA中设置了如图5所示的计算模型。计算模型由3个部分组成：薄壁管、移动刚性墙和固定底板。薄壁管的底端固定在四面受约束的底板上。同时,管的顶端被刚性墙以恒定速度10 m/s进行轴向冲击,冲击距离为管长的70%。

表1 各管角元素数量及平均冲击力预测公式

图5 计算模型示意图

本文初步选取薄壁管的边长为80 mm,管长为160 mm,壁厚为2 mm,分形系数δ=1∶2。薄壁管的材料为铝合金AA6060 T4,其材料的应力-应变曲线如图6所示。该材料具有以下特性：杨氏模量E=68.21 GPa,密度ρ=2 700 kg/m3,泊松比υ=0.3,屈服应力σy=80 MPa,极限应力σu=173 MPa,延展性为17.4%,幂指强化系数n=0.23。在有限元分析中,由于6系列铝合金对应变率不敏感[16],因此在模拟中未考虑应变率的影响。采用LS-DYNA中的123号模型(MAT_MODIFIED_PIECEWISE_LINEAR_PLASTICITY)来模拟铝合金材料,采用20号刚体材料(MAT_RIGID)来模拟刚性墙。

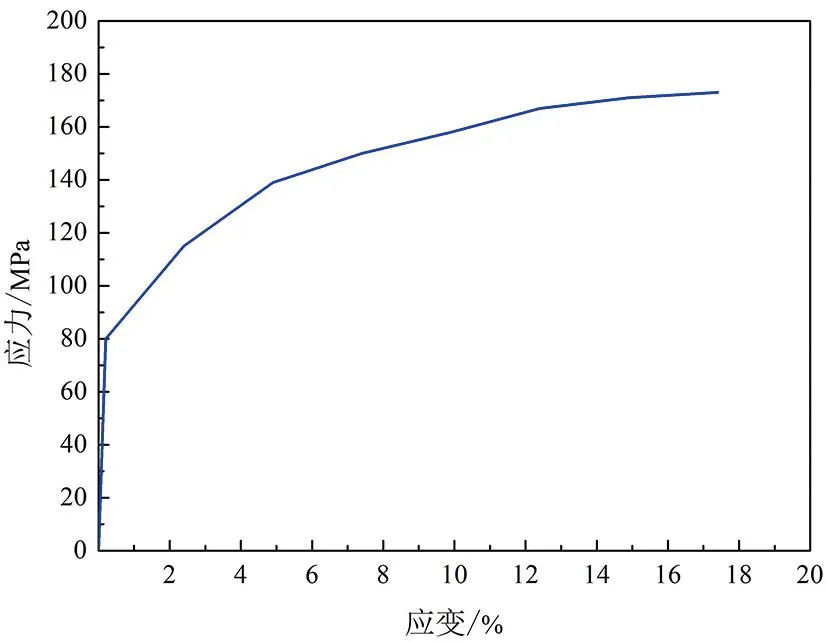
图6 AA6060 T4 铝合金单轴拉伸应力-应变曲线

薄壁管采用LS-DYNA中的Belytschko-Tsay四节点壳单元建模,沿厚度方向采用5个积分点,面内采用2个积分点。为防止管壁的穿透,管壁自身变形产生的接触采用摩擦系数为0.2的自动单面接触算法,管壁和刚性墙之间的接触则采用摩擦系数为0.2的自动点面接触算法[17]。

不同的网格尺寸对数值模拟结果有很大影响。本文选择方形单胞管(SQUARE)进行网格收敛性分析。网格分为5个不同的尺寸：3.0、2.5、2.0、1.5和1.0 mm,图7显示了模拟结果。如图7所示,在网格尺寸小于2.0 mm时,平均冲击力趋于收敛。为了节省计算资源,后续的数值模拟选择2.0 mm的四边形网格。

图7 网格收敛性分析

3.2 有限元模型验证

有限元模型的可靠性直接影响仿真结果的分析。为了验证模型的可靠性与准确性,需要保证整个冲击过程的能量守恒。采用LS-DYNA软件对上述两类模型进行求解计算。为了提高计算效率,采用了简化积分算法和质量缩放。薄壁管的沙漏能与质量增加比较见表2。

有限元分析时,沙漏能不超过内能的5%,质量增加不超过总质量的5%则认为不影响仿真精度。由表2中的结果可知,薄壁管的沙漏能占内能的比例与质量增加的百分比均小于1%, 表明本文计算模型具有较高的可靠性。

表2 各管沙漏能与质量增加比较

4 有限元模拟结果分析

图8显示了各管在轴向压缩下的变形状态。在相同的压缩时间下,随着分形阶数的增加,管壁褶皱的数目也随之增加,波长减小,变形模式也逐渐稳定。高阶比低阶具有更规则的折叠变形,高阶波长明显短于低阶。表明高阶结构在变形过程中形成更多的塑性铰,吸收更多的能量,因此高阶结构可以提高能量的耗散。

(a)4 ms (b)8 ms (c)11.2 ms图8 各管渐进压缩对比图

图9显示了薄壁管的冲击力-位移曲线,从图9可以看出,几类薄壁结构在轴向冲击的过程中力-位移曲线的变化趋势都是相似的。在碰撞开始时,冲击力迅速达到峰值后迅速回落,之后在平均冲击力附近上下震荡,这对应着薄壁管的逐层压溃。

图9 各管冲击力-位移曲线

为了验证推导出的理论模型的可靠性,使用预测公式计算了不同薄壁管的平均冲击力结果,并与数值模拟结果比较,结果见表3。由表3可知,误差均在10%以内,结果吻合较好,表明所推导的理论模型可以有效地预测薄壁管的能量吸收性能。

表3 各管平均冲击力理论预测与数值模拟比较

为了定量研究薄壁管的耐撞性,各管的能量吸收-位移曲线如图10所示。可以发现同种材料,相同壁厚的两类仿生薄壁管随着分形阶数的增加,高阶薄壁管相较于单胞结构能量吸收有了较大的提高。其中一阶结构TFS-1较单胞结构的能量吸收提高不明显,但二阶、三阶结构提高较明显。

图10 各管能量吸收-位移曲线

薄壁管的比吸能如图11所示。第一类分形薄壁结构TFS-A2、TFS-A3的比吸能分别是单胞结构SQUARE的2.51和2.96倍,第二类分形结构TFS-B2、TFS-B3的分别是单胞结构SQUARE的2.44和3.45倍。在阶数相同的情况下,二阶的TFS-B2和TFS-A2的比吸能相差接近,但三阶TFS-B3和TFS-A3的相差增大。TFS-B3的结构最复杂,吸能效果也最好。可以明显地看出高阶薄壁管比吸能有较大的提高,这意味着高阶结构每单位质量可以吸收更多的能量,表明高阶结构相对于低阶结构具有更好的能量吸收能力。由此可以看出,树状分形设计是提高薄壁结构吸能特性的一种有效设计。

对于载荷效率CFE来说,其比值越接近于1,碰撞过程中波动越平缓,可以避免冲击过程中产生较大的减速度,有助于提高乘员的安全性。从表4中可以看出,随着阶数的增加,两类结构的载荷效率都有明显提升,其中高阶薄壁结构TFS-B3达到了87.8%,说明在碰撞压溃过程中冲击力保持在较平稳状态,具有较高稳定性。TFS-A3和TFS-B3的CFE相对于SQUARE提升了84.5%和97.7%。因此,这表明树状分形设计在压缩稳定性上优于单胞结构。