基于电感特性的磁阻式球形电机无传感器位置检测*

嘉 奖，王群京，3，鞠鲁峰，3，许家紫

（1.安徽大学 电气工程与自动化学院，安徽 合肥 230601；2.高节能电机及其控制技术国家地方联合实验室 安徽大学，安徽 合肥 230601；3.工业节电与用电安全安徽省重点实验室 安徽大学，安徽 合肥 230601；4.工业节电与电能质量控制安徽省级协同创新中心 安徽大学，安徽 合肥 230601）

0 引 言

当前随着现代制造业逐渐向着自动化智能化的方向发展，对能够实现多自由度执行机构的要求也日益增加［1］。传统多自由度运动执行机构均为多个单自由度电机与传动机构耦合而成，其尚存结构复杂、抗干扰性差和控制困难等问题［2，3］。因此一种新的能够实现三自由度运动的磁阻式球形电机被提出，以解决上述问题［4］。

球形电机具有够实现三自由度运动的特点，因此不能以开环方式驱动，必须获得准确的转子姿态位置。目前各国学者在球型电机的位置检测和驱动控制方面进行了广泛的探索。文献［5］采用了霍尔传感器进行转子位置检测，对球形电机的磁场模型精度要求较高，且容易受到环境磁场干扰。文献［6］提出了基于微机电系统（MEMS）的位置检测方法，直接在球形电机输出轴上安装MEMS传感器来实现对转子偏转角度的测量，但存在零点漂移的问题。文献［7，8］采用了一种基于光电编码器的位置检测方法，利用3个增量式光电编码器组合测量的方式得到转子姿态角度，运算速度较快，但成本较高。文献［9，10］采用机器视觉的方法来实现球形电机位置检测，通过安装高速摄像头获取转子运动的画面，通过多目标算法处理计算姿态角，此方法的精度易受环境光强的影响。以上球形电机转子姿态检测方法的共同点是都需要在转子轴或定子壳上安装位置传感器来实现，这些传感器所占用的空间较大，为球形电机的实际安装和应用造成了负面影响。

为解决上述问题，本文提出了一种基于电感特性的磁阻式球形电机无传感器位置检测方法。根据采集转子在不同姿态角度下的电感特性，通过机器学习算法--极限学习机（extreme learning machine，ELM）来建立针对转子自旋角度的回归预测模型，实现磁阻式球形电机的无传感器位置检测。

1 磁阻式球形电机基本结构

本文研究对象为一台磁阻式球形电机，其结构如图1所示，主要结构参数如表1所示。

图1 新型磁阻式球形电机结构

该磁阻式球形电机主要结构由安装有铁心的定子球壳、冲片叠压方式制成的转子、集中绕组式定子线圈和输出转轴4 个部分组成。定子线圈被分为3 层，均匀地缠绕在定子球壳内部的铁心上，每一层有8 个线圈，整体共计有24个线圈。转子采用凸极式结构设计，用以提升输出转矩，转子齿共有6个，由硅钢片堆叠而成，外部采用球形的聚碳酸酯工程塑料将其固定。由于定子线圈位置的限制，定子坐标系下转子输出轴沿X轴和Y轴旋转的倾斜角度α和β范围为-30°～30°，沿Z轴的自旋角度γ为0～360°。

2 磁阻式球形电机电感特性分析

2.1 电感测量平台搭建

为了获得转子偏转角与线圈电感之间的数值关系，本文设计了一个测试实验平台，如图2 所示。它包括待测的磁阻球型电机、基于STM32F4 的数据采集与处理模块、功率放大电路、电感检测电路和角度检测仪等部分组成。

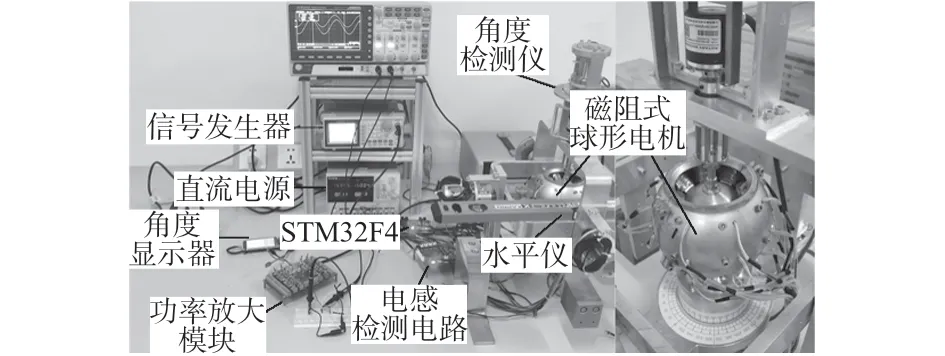
图2 磁阻式球形电机实验平台

其中，角度检测仪采用式光电编码器来记录转子实际偏转角度，以供后续进行预测模型搭建和精度校验。水平仪用于为角度检测仪校零。由于信号发生器的负载限制，添加了一个功率放大模块用于稳定检测信号幅值。STM32F4用于数据采集与处理，电感检测的基本原理如下：

为定子线圈串联一个标准电阻R，通过信号发生器产生固定频率的交流正弦波，经功率放大电路增大幅值并消除杂波干扰，为电感测量电路提供稳定的检测信号。利用示波器检测并记录此时的电路总输入电压与标准电阻分压。

由于电阻上的分压均为同相位，根据标准电阻分压，可以得到定子线圈电阻部分的分压

最后，根据阻抗公式

2.2 电感特性分析

磁阻式球形电机在运动过程中，12 组定子线圈上的电感均发生了不同的变化，因此需要对12 组线圈标定编号，以方便分析运动过程中不同线圈的电感特性。首先规定转子齿在未发生倾斜运动时与赤道线上某个定子线圈对齐时为起始位置，此定子线圈组为1＃线圈组，后续按照转子旋转方向，赤道线上剩余的3 组线圈被定为2＃，3＃，4＃线圈组。上下2层线圈也按照同样的方式标定，具体的编号如图3所示。

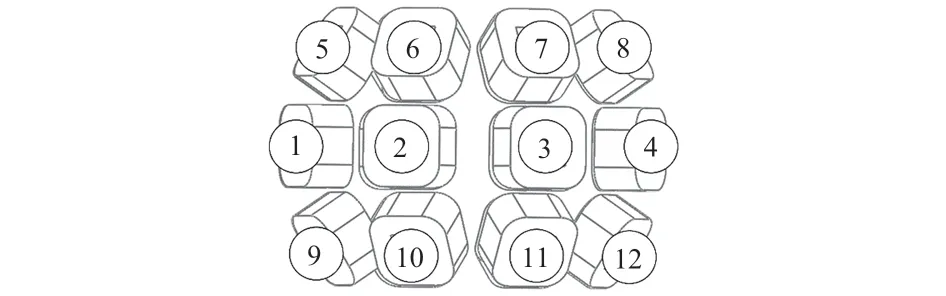
图3 磁阻式球形电机线圈组编号示意

2.2.1 中心点自旋运动

定子坐标系下，保持α与β为0°，γ从0°变化至360°，即转子在未倾斜的状态下自转1 周，得到的12 组线圈电感与自转角度的关系如图4所示。

图4 中心点自旋运动电感特性

2.2.2 轴向倾斜运动

定子坐标系下，保持γ 和β 为0°，α 从-30°变化至30°，得到的12组线圈电感与倾斜角度的关系如图5所示。

图5 轴向倾斜运动电感特性

2.2.3 给定倾斜角旋转运动

定子坐标系下，给定倾斜角度β 为15°，α 保持为0°，γ从0°变化至360°，即转子在倾斜15°的状态下自转1 周，此时转子输出轴的运动轨迹为一个圆环，得到的12 组线圈电感与旋转角度的关系如图6所示。

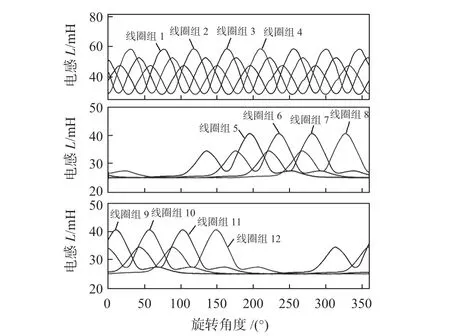
图6 给定倾斜角旋转运动电感特性

3 基于ELM的角度预测模型

3.1 预测模型搭建

通过分析磁阻式球形电机的电感特性可知，在不同运动方式下，磁阻式球形电机12组定子线圈上的电感与角度之间呈明显的线性关系。考虑到输入数据维度较高，本文选取了一种机器学习算法--ELM，来建立起12 组电感数据与角度之间的回归预测模型。

目前常见的单隐层前馈神经网络有反向传播（back propagation，BP）神经网络和支持向量机（support vector machine，SVM）等算法，其核心思想都是通过不断优化训练神经网络内部的权值和偏差值来实现对训练集数据的分类或回归，因此容易出现迭代训练过程较长与限于局部最优的问题。ELM与上述算法相比，其最大的优点在于隐含层参数是任意生成的，因此，可以做到先建立隐含层节点再输入训练集数据，其输出层的权重则是依靠逆矩阵计算得到，极大地提升了模型训练速度，但同时也降低了模型的稳定性［11，12］。

为了改善这个问题，可以引入正则化系数C 和径向基核函数ΩELM＝exp（-‖xi-xj‖2／2σ2），随后采用粒子群优化（particle swarm optimization，PSO）算法对这2 个参数进行优化，使得模型的均方根误差尽可能低，以此提升模型的整体精度。基于PSO算法优化的极限学习机整体建模过程如图7所示。

图7 基于PSO算法的ELM模型训练过程

3.2 验证结果

将样本库中的数据组分为训练集和测试集，将训练集中的12组定子线圈电感L1～L12作为输入，角度检测仪所测得的实际角度作为输出，分别建立默认参数下的ELM 回归预测模型和基于PSO 算法优化后的ELM 回归预测模型。其中PSO种群数量设置为50，最大迭代次数100，惯性因子w为0.9，加速常数c1和c2均为2。模型训练完成后，将测试集的12组定子线圈电感L1～L12作为输入，通过回归模型得到的预测角度与实际角度做对比，验证结果如图8所示。

可以看出，在不同运动方式下，经过PSO 优化后的ELM回归预测模型的预测效果均远好于默认参数下的ELM模型，其最大误差不超过1°，展现出了较好的位置检测能力。

4 结 论

本文提出了一种基于电感特性的磁阻式球形电机无传感器位置检测方法，并搭建实验平台验证了该方法的可靠性。该方法最大的优点在于无需在球形电机本体结构上安装位置传感器，极大地降低了球形电机的实际安装与应用所需的空间，增强了系统整体稳定性，同时还具有较高的精度，为磁阻式球形电机闭环追踪控制打下了坚实的基础。

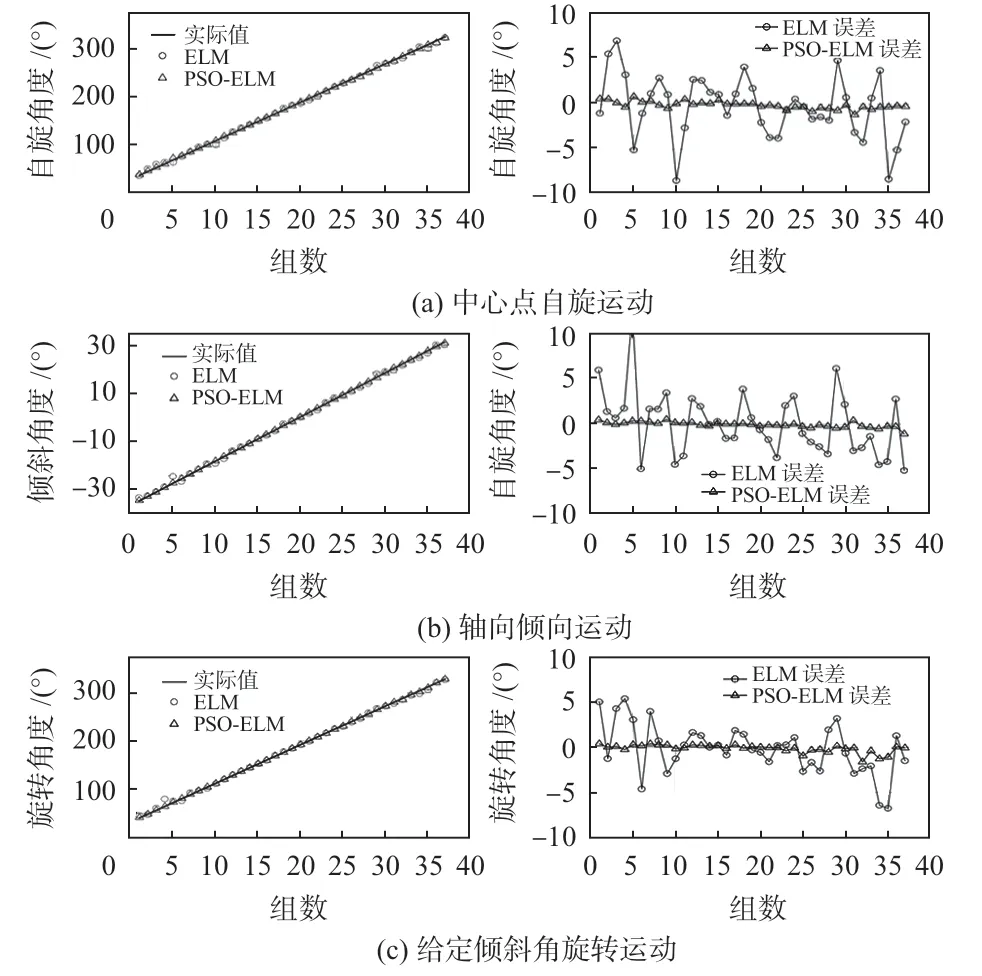
图8 不同运动方式下的预测结果与误差