基于管材扭转试验确定材料弹塑性本构的方法*
2024-01-12赵玉杰刘小涛马咪娜陈宏恩王姝丹孙军帅
赵玉杰,刘小涛,马咪娜,陈宏恩,王姝丹,孙军帅
(1.庆安集团有限公司,陕西 西安 710077; 2.西安交通大学,陕西 西安 710049)
0 引 言
在飞机传动系统中会大量使用扭力管传递扭矩,考虑维修性,扭力管和作动系统之间往往通过法兰盘连接。这类扭力管大部分是将法兰盘和等直段分别加工后通过铆钉或焊接连接,而这两种连接方式都会明显降低产品整体强度和疲劳性能。因此,如何避免TC4钛合金扭力管在一体成型工艺中的连接部位出现应力集中成为研究热点。而新工艺的塑性加工及热处理过程会使材料的力学性能发生变化[1-2],尤其是塑性阶段,因此,需要通过试验确定该工艺成型后材料的弹塑性本构。
真实应力应变曲线反映了材料受力变形的全过程,是确定结构真实破坏强度和抵抗变形能力的重要依据。完整准确的弹塑性本构可以直接提高设计和分析能力,有效避免设计强度不足或者过设计的问题。最常用的获取金属材料真实应力应变的方式是进行标准件(如棒材或管材等)拉伸试验[3],但塑性成型的金属管材往往表现为横观各向同性[4-5],其在横截面的切向和轴向拉伸的应力应变曲线有一定差异,不能反映扭转性能。文献[6]中介绍了一种通过实心圆轴扭转试验确定真实应力应变关系的方法,但对于管材,尤其是厚壁管材(一般指壁厚与半径之比大于1/10或1/5),由于塑性阶段截面内应力分布非线性且不可忽略,所以很难通过管材扭转试验获得屈服后的材料真实应力应变曲线。
笔者根据材料力学基本假设,推导出通过管材扭转试验获得材料弹塑性本构的计算公式,通过对应用此方法获得的材料属性进行数值仿真并与试验结果进行比较,验证了此方法的可行性和实用性,为类似特殊管材成型工艺对材料力学性能的影响研究提供支持。
1 管材扭转弹塑性本构计算方法
对于等直的圆环截面扭转试件,在加载至破坏或失稳之前,可以始终认为材料力学中的平面假设及小变形假设成立,即对图1所示的标距段内任一微段,在距中心ρ处,有以下公式:
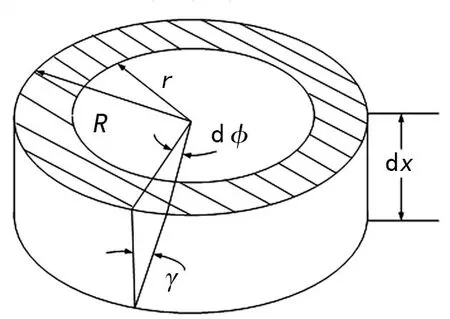
图1 试件微段示意图
(1)
式中:γ为该处的切应变;L0为标距段的长度;φ为标距段两端相对转角。
对于任意给定时刻,由于φ是与选点位置无关的固定值,因此对于试件横截面沿径向方向的切应变为线性分布,其切应力与材料的真实应力应变曲线的某一部分有相似分布,而整个加载过程的横截面应力分布变化是在式(1)前提下材料应力应变曲线的横轴压缩变换(这一性质以下简称分布相似性)。因此,可将整个加载过程分为三个阶段,即弹性阶段、部分屈服阶段和完全屈服阶段,如图2所示,同时记截面中心为点O,任选一径向与截面外侧交点为A,与截面内侧交点为B,R为管材外径,r为管材内径。
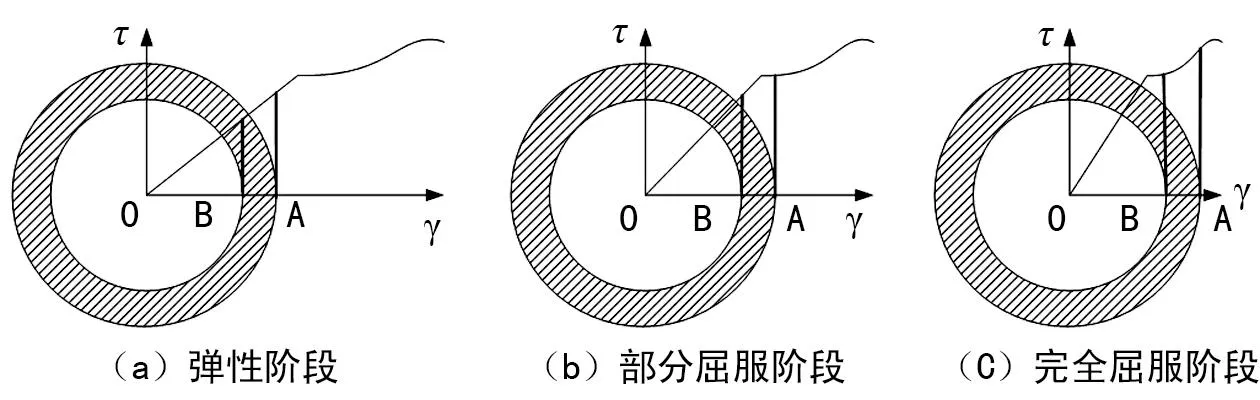
图2 加载三阶段示意图
对于弹性阶段,可直接根据国标[7]确定其剪切模量G、真实规定非比例扭转强度TpA及对应扭转角度φpA,并进一步计算得到材料的切应力屈服极限τp及对应的切应变γp。
设时刻1(见图3(a))扭转角为φ1,横截面总扭矩为M1,横截面上AB段内各点切应力分布为τ1=τ1(ρ)。因此有:

图3 部分屈服阶段切应力分布

(2)
同样的,时刻2(见图3(b))时扭转角增至φ2,横截面总扭矩增大至M2,横截面上AB段内各点切应力分布为τ2=τ2(ρ)。设k=φ2/φ1,同时在线段0A内另标记两点A′、B′,令OA′=R/k,OB′=r/k。则有:
M2=M2B′A′-M2B′B+M2A′A
(3)
根据分布相似性,有τ2(ρ)=τ1(kρ),因此对于B′A′段,令ρ′=kρ,有:
(4)
部分屈服阶段试件截面内侧仍处于弹性阶段,因此对B′B段,有:

(5)
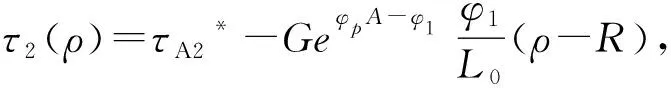
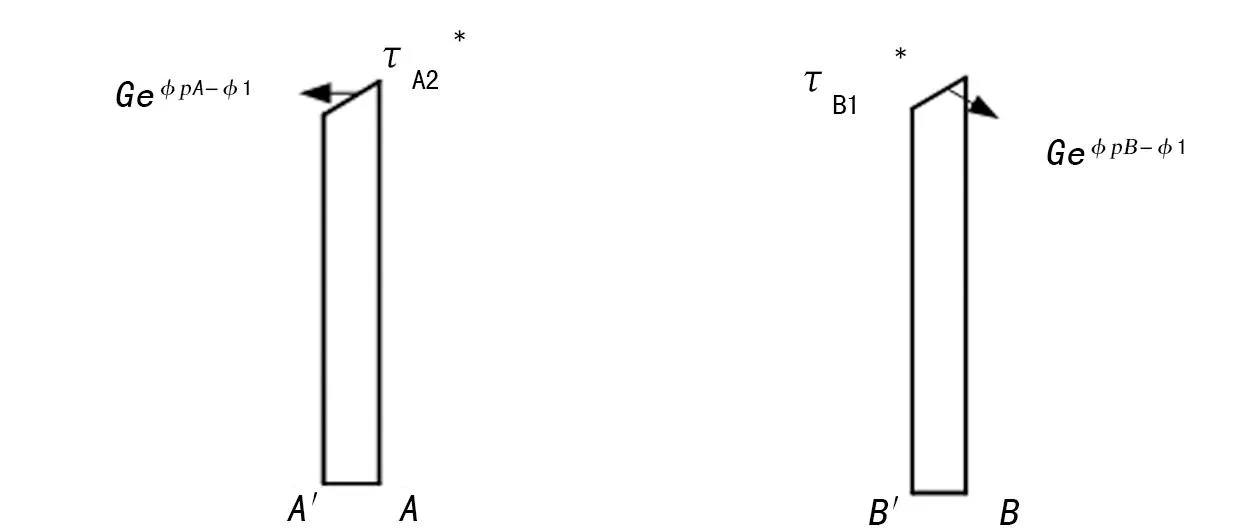
图4 部分屈服时刻A′A段内切应力 图5 完全屈服阶段B′B段内切应力
(6)
结合式(3)~(6),可知:
τA2*=
(7)

(8)
同样的,可知:
(9)
(10)
对于匀速加载和恒定采点频率的管材扭转试验,可得到一组扭矩-扭转角数据[Mi,φi]i=1,2…n,应用上述分析,可得到对应的切应力切应变曲线:
(11)
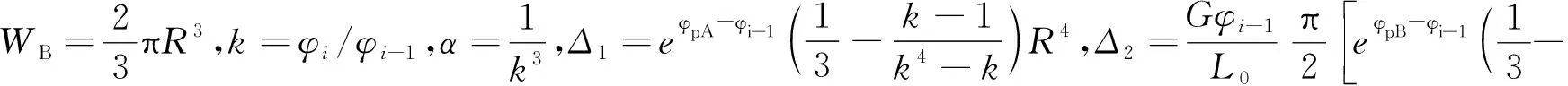
通过上述方法编辑程序对管材扭转试验结果进行处理,即可得到材料的真实弹塑性本构。需要注意的是,由于公式会放大试验中的力矩波动,尤其是力矩变化较小的后半段,直接处理得到的曲线可能会有较大的“毛刺”,可通过适当的选取k值并结合滑动平均法等对获得的真实应力应变曲线进行光滑处理。
2 管材扭转试验确定真实弹塑性本构
根据国标[7]制备TC4钛合金管材试件并进行扭转试验,试件结构及尺寸如图6所示。
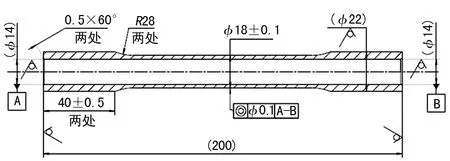
图6 管材试件形式及尺寸
试验时一端固定,另一端放开轴向平动自由度,以20°/min匀速加载,并以800次/min的频率采集并记录扭矩及扭转角。试验过程如图7所示,扭矩-扭转角数据如图8所示,根据上节分析内容编辑程序计算处理得到的真实弹塑性本构如图9所示。

图7 管材扭转试验
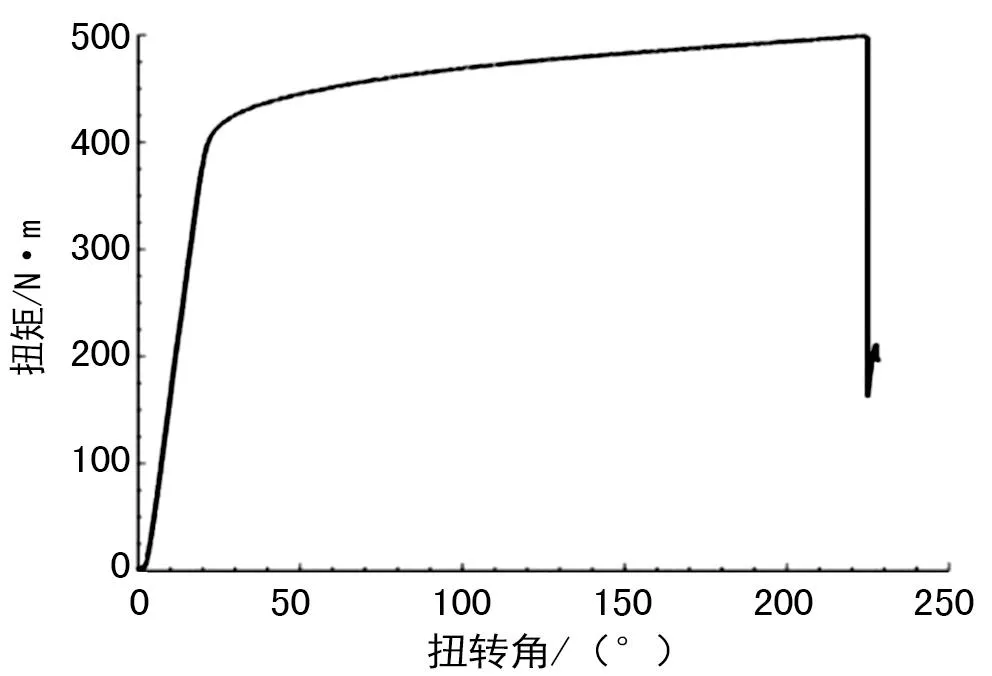
图8 试验结果
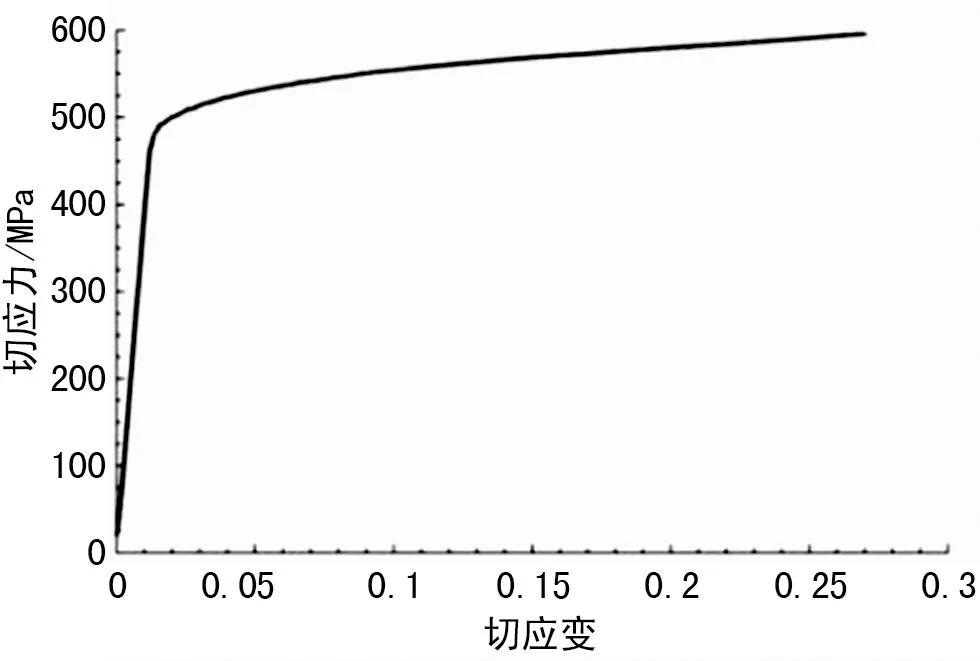
图9 真实切应力-切应变关系
3 材料弹塑性本构的验证
为了验证根据公式和试验数据获得的材料真实弹塑性本构,通过有限元仿真分析计算与试验结果对比,确定文中分析方法的准确性和合理性。
基于ANSYS仿真软件并根据试件尺寸建立相同的有限元模型,采用六面体实体单元划分网格,单元数45 878,节点数219 628,如图10所示。试件材料根据上节获得的弹塑性本构进行设置,将一端固定,另一端放开轴向平移自由度,同时施加轴向转动位移载荷,如图11所示,模拟试件的扭转试验过程。提取约束端反力矩,做出力矩-扭转角曲线与试验数据进行对比,如图12所示。
图10 有限元模型

图11 约束与加载
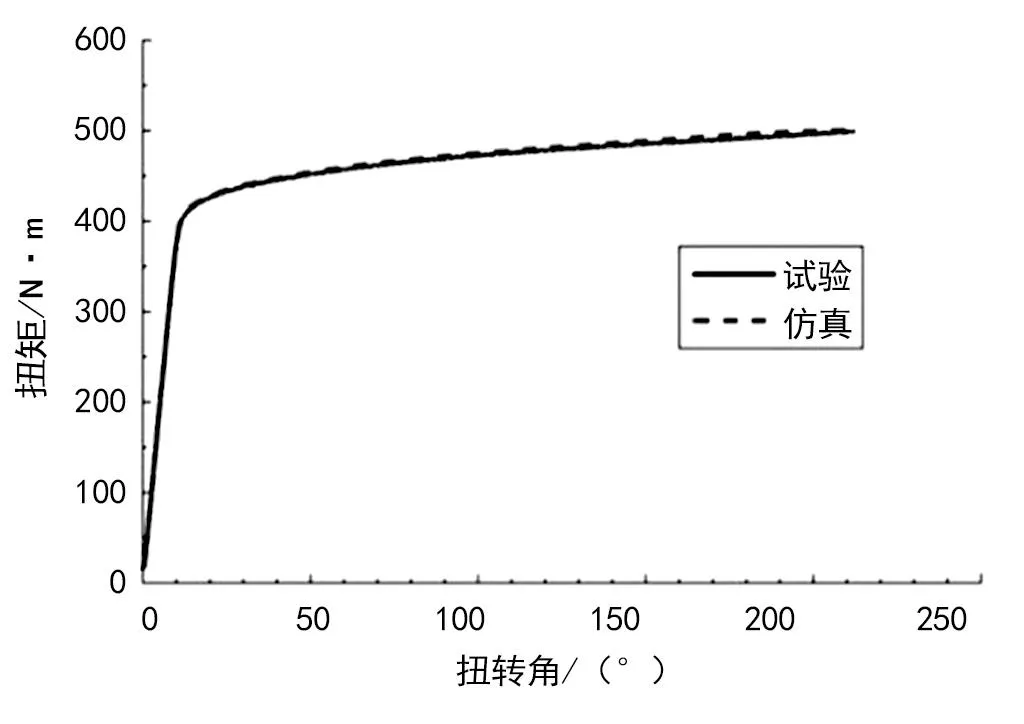
图12 仿真与试验结果对比
从图12可以看出,在整个加载过程中仿真结果与试验数据的力矩-位移曲线几乎重合,最大误差仅有约0.8%,证明该基于管材扭转试验中根据分布相似性确定真实弹塑性本构的方法是合理且准确的。
4 结 论
为分析管材成型工艺对材料力学性能的影响,文中基于扭转平面假设及分布相似性,推导出基于管材扭转试验确定材料真实弹塑性本构的计算方法,并通过编程实现。采用该方法对TC4钛合金管材扭转试验数据进行处理可获得材料的真实切应力-切应变曲线,通过对比有限元仿真分析结果与试验结果,得出以下结论。
(1) 对整个加载过程,仿真结果与试验结果基本一致,最大误差不超过0.8%,证明了该分析方法的准确性与工程实用性,为新工艺成型扭力管的精确设计及应用提供了有力支撑。
(2) 考虑到管材扭转试验在断裂前可能出现失稳屈曲,从而导致平面假设及分布相似性不再成立,因此文中所提方法对细长管材或薄壁管材在大变形阶段的应用有一定的局限性。
