基于载荷次序修正的连续损伤疲劳累积损伤模型*
2024-01-12薛齐文
刘 源,薛齐文
(大连交通大学 土木工程学院,辽宁 大连 116028)
0 引 言
机械设备工作运行期间不断承受着外部变幅循环载荷的作用,导致结构不断地发生损伤,疲劳损伤不断累积直至结构发生疲劳破坏,这种破坏与结构的材料性能有着密不可分的关系[1]。因此,众多学者针对结构的材料性能在变幅载荷作用下呈现出的规律展开了大量的研究,并提出了大量不同的数值模型,这些数值模型为结构的设计和运行提供了理论基础。但是现有的理论模型大多存在着物理参数过多的问题,且有些参数的值难以直接通过实验测定,不能应用于实际工程中去。
近些年来,国内外学者开始针对材料损伤本身展开研究,其中大部分研究方法都是针对线性理论。在线性理论中,应用最为广泛的是Miner损伤法则,该法则具有形式简易、原理和规则较为简单的优势,但该模型在计算时,载荷之间相互独立,未能考虑载荷相互作用,从而忽略了载荷加载的次序[2-3]。而交变载荷在循环中,大部分金属材料在描述损伤与循环载荷之间的关系时表现出了极高的非线性。因此,在线性理论提出之后,国内外众多学者开始提出了大量的非线性损伤模型[4]。这些非线性损伤模型从不同方面考虑到疲劳损伤受到来自内部和外部等因素的影响,其中比较典型的有Chaboche等[5]提出的连续损伤力学模型以及杨晓华等[6]将韧性耗散能与连续损伤理论结合得到的新模型等。这些方法可以从一定程度上考虑到材料自身的损伤特性以及累积损伤效应,且预测结果优于线性损伤模型,但它们仍忽略了多级载荷加载历程中相邻两级应力幅值间的相互影响,因此需要对此进行进一步探讨与优化。
基于以上分析,笔者对在交变载荷作用下连续损伤理论模型未考虑载荷次序的影响进行了修正,并利用载荷比的形式构建了载荷交互因子,并将构建的载荷交互因子引入原始模型中,提出新的修正模型。建立的新模型将会在二级变幅载荷下对不同结构材料的疲劳寿命进行预测,然后与疲劳试验数据对比,以进行可行性与有效性验证,并与原始模型等进行对比分析。
1 原始模型
结构发生疲劳损伤时,需要注意以下几点[7]:①结构存在着初始微小裂纹形核以及后续发生的扩展阶段;②二级或多级加载模式下疲劳的累积损伤效应;③疲劳极限在出现初始损伤后发生大幅减小的情况;④应力的平均值对结构疲劳极限应力及材料应力-寿命曲线的影响。
基于上述四点考虑,Chaboche提出了一种可以描述材料性能不断劣化过程的连续损伤理论模型,表达式如下:
dD=f(…)dN
(1)
式中:函数f中存在的变量包含应力、塑性应变、温度和结构损伤等,且加载的应力值与造成损伤的因素变量不可分离表达。当以应力的方式进行加载时,式(1)可以描述为:
(2)
式中:指数φ是关于σmax和σm的函数;σmax和σm分别为最大应力和平均应力。
根据文献[6]中的研究成果可知,需将材料的韧性耗散能与连续损伤理论结合并积分。积分边界为:循环次数n=0时,损伤D=0;当循环次数n=Nf时,损伤D达到极限1。由此得到连续损伤公式为:
(3)
式中:ni为i级载荷对应的循环次数;Nfi为对应等级下的疲劳寿命。结合等效损伤理论,可将其推广至二级应力加载下非线性疲劳累积损伤模型:
(4)
代入式(3)得:
(5)
式中:n2′为一级载荷循环次数n1等效下的二级循环次数。推导式(5)可得:
(6)
推导出在二级载荷加载下,剩余损伤表达式为:
(7)
由式(7)可知,基于连续损伤理论建立的非线性疲劳累积损伤模型形式简单,所含物理参数较少,具有颇高的工程实际应用价值。但是,它未能考虑到载荷之间的相互作用对疲劳寿命的影响,使得其对结构的剩余疲劳寿命预测精度受到一定的影响,因此需要对此模型进行相关的修正。
2 修正模型
针对上述模型未能考虑二级加载方式下变幅载荷应力幅值间的相互作用的问题,有学者提出了可用载荷比的形式来描述此相互作用。两级载荷间的差距大小决定了相互作用影响的程度[8,9],文中采用应力比的二次方形式对上述模型进行修正:
(8)
式中:αi为载荷相互作用因子。
在二级载荷作用下,由等效损伤原理可得前两级损伤之间的关系为:
(9)
式中:n2′是依据等效损伤原理将应力σ1下作用n1次等效为应力为σ2下作用的次数。
按照式(9)中推导可得二级载荷下等效损伤循环比:
(10)
则二级载荷下剩余疲劳寿命为:
(11)
式中:下标cp表示相应级别应力下模型的疲劳寿命预测值。
式(11)即为所提改进非线性疲劳损伤模型。模型中既包含了前后两级载荷比的交互因子,还包含了实时损伤函数,形式简单,没有引入多余的参数,这样既保证了载荷加载次序、载荷间相互作用的影响,又不需要引入额外其它参数,适用于实际工程中的疲劳寿命预测分析。
3 算例分析
为验证文章所提修正模型的可行性,将根据收集和整理文献中构件(45号钢、16Mn)的疲劳试验数据进行剩余寿命预测。为了更好地反映模型的预测精度,文中将修正模型的预测结果与Miner模型、原始模型的预测结果进行对比分析。
3.1 45号钢疲劳寿命预测结果对比分析
45号钢是车辆工程中的常见材料。根据文献[10]中45号钢的二级加载试验数据,将试验值与不同模型损伤预测结果进行比较,得到各个模型与试验数据实测值的误差,以此为依据进行对比分析,具体试验加载参数与疲劳寿命预测结果如表1所列。
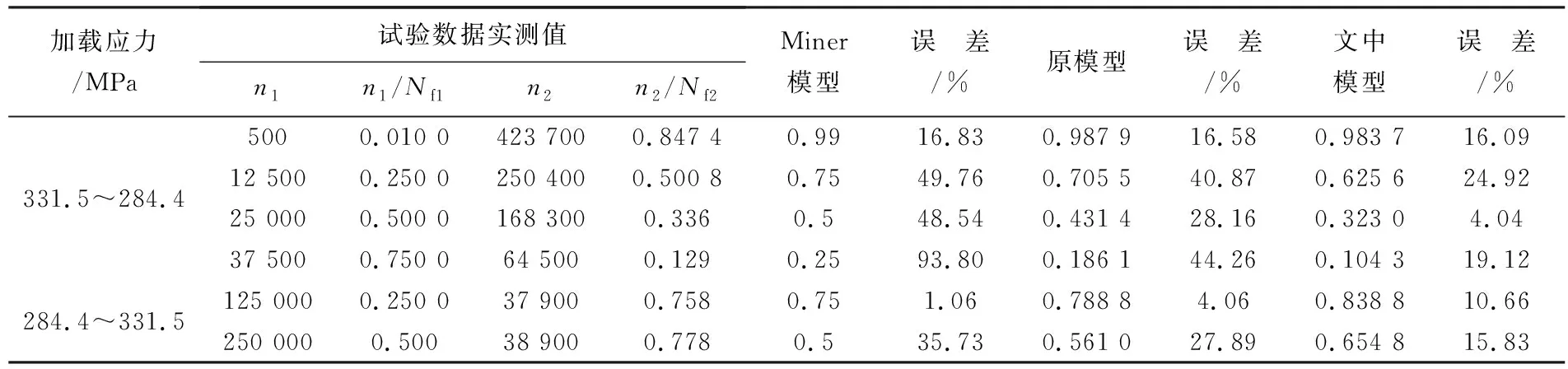
表1 45号钢试件两级加载下疲劳试验数据与各模型疲劳寿命预测值
3.2 16Mn疲劳寿命预测结果对比分析
16Mn是被广泛应用于建筑、汽车以及石化等领域的材料,因其具有高耐磨性,高强度和抗腐蚀等优点,常被用来制造精密零件。根据文献[11]中16Mn的二级加载试验数据,将试验值与不同模型的损伤预测结果进行比较分析,得到各个模型与试验数据实测值的误差,并以此为依据进行对比分析,具体试验加载参数与疲劳寿命预测结果如表2所列。
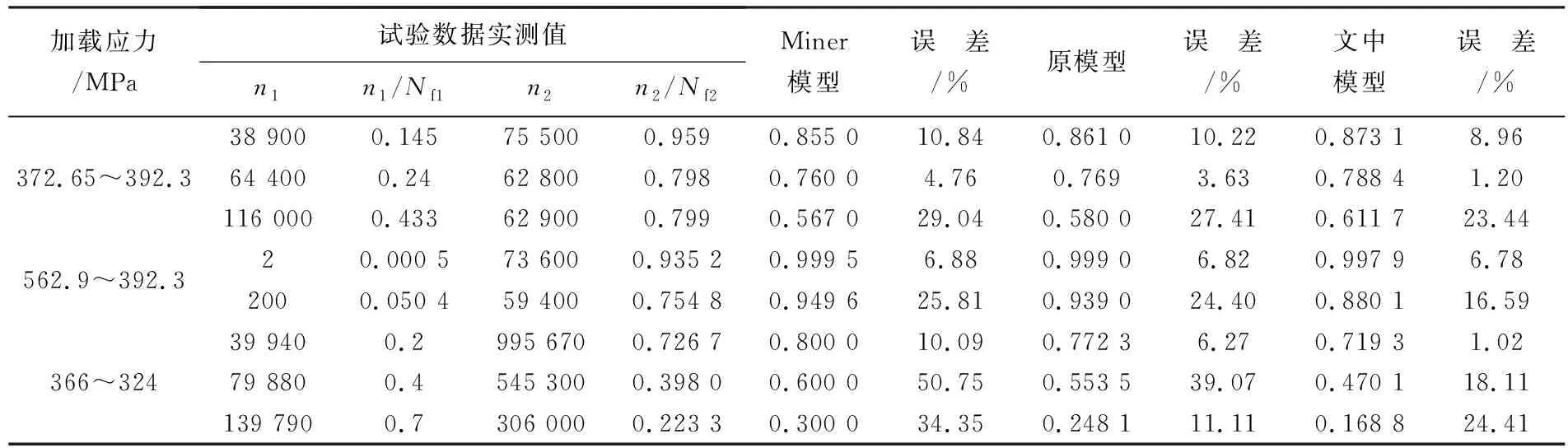
表2 16Mn试件两级加载下疲劳试验数据与各模型疲劳寿命预测值
根据上述两个算例,文章模型与Miner模型、Ye模型进行剩余疲劳寿命估算对比,分别计算各模型与试验数据实测值的误差,并把三种模型在高载荷-低载荷(H-L)加载顺序与低载荷-高载荷(L-H)加载顺序下不同材料的预测值与试验值的比较分析如图1、2所示。

图1 H-L载荷次序加载下疲劳寿命试验值和预测值比较
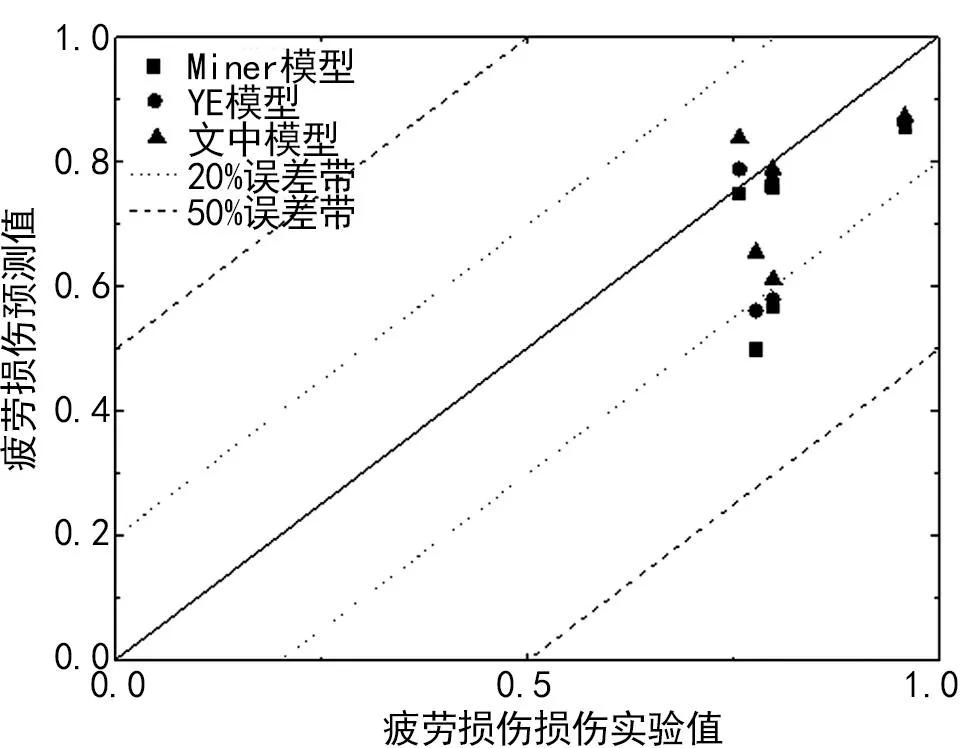
图2 L-H载荷次序加载下疲劳寿命试验值和预测值比较
通过分析表1~2可知,使用Miner模型的平均误差分别为40.95%、21.56%,使用Ye模型的平均误差分别为26.89%、16.12%,使用文章修正模型的平均误差分别为15.11%、12.56%。相比于Miner模型分别提升了25.84%、9.00%,相比于原始模型分别提升了11.78%、3.56%,因此,文中模型预测精度略有所提高,可以更为有效地进行疲劳寿命预测,具有一定的工程实用性。
4 结 语
文章利用相邻载荷比的二次方建立新的载荷相互作用因子,构建一种可行的连续损伤修正模型。所改进的预测模型可有效地处理变幅载荷间的相互作用对不同材料疲劳损伤累积的影响,且根据不同材料的疲劳寿命对比结果发现,在二级载荷的作用下,改进模型对疲劳寿命预测的能力有了一定提升,预测分析结果也比原始模型以及Miner法则更加接近于真实的试验结果。新的改进模型可以更好地表征疲劳损伤演变特征,适用于工程实际结构的疲劳寿命预测。
