高温超导滤波器在电磁抗干扰中的技术和应用

刘天康,刘海文

(1.国家无线电监测中心 乌鲁木齐监测站,乌鲁木齐 830000;2.西安交通大学 信息与通信工程学院,西安 710000)

0 引言

超导材料的发现,是现代物理学最伟大的发现之一。超导体的零电阻特性在电磁波传输控制方面发挥着极其重要的作用,特别是在高灵敏度微波滤波器件设计与应用方面,基本满足了军事、航空航天、射电天文、深空探测等应用场景[1-3],但随着电磁环境的不断恶化,对微波滤波器件的性能要求更加严苛。

射电天文科学观测是人类认识宇宙的基本途径,其完全基于接收源于宇宙的无线电波,从而对宇宙起源等科学问题开展研究。但无线电频谱是非常重要的战略资源,根据无线电国际主管组织国际电信联盟发布的全球无线电频率划分情况[4],目前未被人类使用的频率越来越少,并正在研究将未分配利用的275GHz以上的频谱资源进行分配使用。使用最活跃的地面公众移动通信频率已经从数百MHz的分米波跨越到了数十GHz的毫米波,目前正在研究数百GHz的太赫兹频段应用到未来的地面公众移动通信中。中国已在2023年6月最新的无线电频率划分规定中,在全球率先将6GHz频段划分给国际移动通信(international mobile telecommunications,IMT)使用[5]。随着5G、6G、低轨卫星星座等大量工作于新频段的无线电通信系统的应用,射电天文和深空探测等领域受干扰的情况将愈发严重,根据长期无线电环境监测显示,卫星导航频率和地面移动通信频率是射电望远镜最大的干扰源,如图1所示[6-7]。

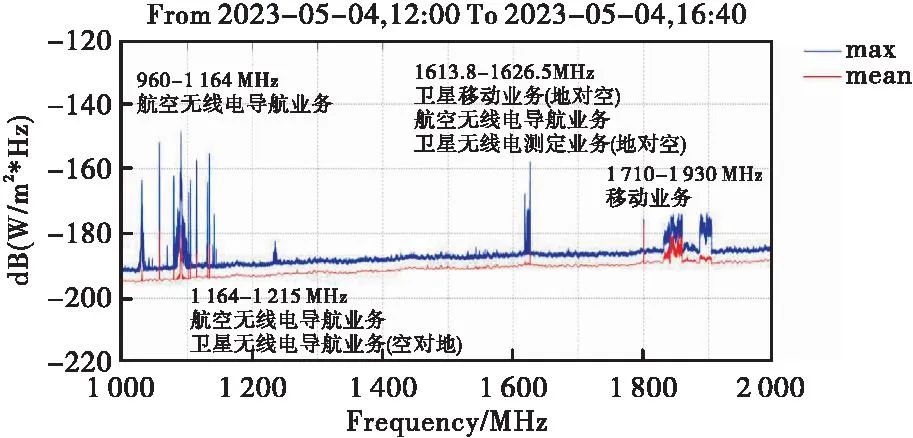
图1 某射电天文望远镜1GHz～2GHz电磁环境频谱图Fig.1 Electromagnetic environment spectrogram in 1GHz-2GHz for the radio astronomy telescope

由于大量无线电信号的干扰造成可观测频谱资源的日益减少,射电天文望远镜对于电磁抗干扰的需求越来越迫切,而采用高温超导材料设计的陷波滤波器既能满足射电信号高灵敏度的接收要求,也能满足电磁抗干扰的需求,是射电天文望远镜保持甚至是提升性能最佳的技术方案之一,在射电天文观测和深空探测方面具备极大的电磁抗干扰和高性能特性的应用潜力。因此,很多宽带或窄带陷波滤波器被设计出来以满足不同领域的抗干扰需求[8-11],文献[8]在馈线端采用交趾耦合线的技术抑制UWB频段内250MHz的宽带信号[8],文献[9]在主谐振器内部嵌入两个短路环形谐振器抑制UWB频段内600MHz的宽带信号[9],文献[10]在主谐振器上耦合一对四分之波长谐振器来产生陷波[10],文献[11]通过在低通滤波器中添加4组叉指电容环路谐振器实现了500MHz的宽带陷波[11],然而以上工作的设计技术并不太适用于射电天文这类需要对窄带干扰信号进行抑制的应用场景,同时打孔接地结构也不适用于超导滤波器的设计和制造。而公开发表的采用高温超导技术设计的陷波滤波器则非常少,文献[12]利用高温超导技术采用4个复合左右手零阶电路产生陷波,但实测响应的频率漂移现象较严重,达到了设计带宽的20%[12]。LIU H W等基于十余年高温超导滤波器领域的研究和设计成果[13-15],在电磁抗干扰方面做了一些工作,用于满足射电天文、深空探测等场景对高性能、抗干扰微波滤波器的迫切需求,取得了一些研究成果[2-3,16]。

本文选取本团队的部分工作,介绍高温超导滤波器在电磁抗干扰方面的研究情况,主要有基于多模谐振结构的高温超导单/双陷波宽带滤波器和基于双阶跃阻抗双模谐振结构的高温超导单陷波多通带滤波器的研究和设计。本团队研究工作的创新点在于,一是在L波段应用高温超导陷波滤波器技术服务于射电天文望远镜的抗干扰和观测性能提升场景,二是提出两款新型多模谐振电路用于宽带和多通带的设计,三是设计的滤波器的仿真和实测结果吻合度较高。

1 陷波滤波器设计原理

本文研究和介绍的高温超导陷波滤波器均为二端口微波器件,可以采用二端口微波网络的散射参数分析方法进行综合分析进而指导设计工作。对于谐振器可以采用经典的传输线理论和奇偶模分析方法对谐振模式开展分析工作,具体分析方法在后续谐振器分析中进行详细介绍。

滤波器的频率响应特性在通带内表现为传输而在阻带内表现为衰减,可以由散射参数中的S21来表示,如式(1)所列:其中,ε为波纹系数,Fn(Ω)为特征函数,Ω表示频率。

(1)

而滤波器在阻带内的衰减特性可以表示为式(2)所列:

(2)

公式(1)和公式(2)在滤波器设计中极为重要。设计陷波滤波器时,可将陷波作为衰减特性来设计。陷波滤波器的理想散射矩阵与带通滤波器的理想散射矩阵一致,如式(3)所列。

(3)

在设计滤波器时,根据设计指标,结合理论计算得到滤波器阶数、极点、零点和耦合矩阵,使用电磁仿真软件对设计的电路进行仿真,根据滤波器的理论响应来优化设计的电路版图。其中,要对滤波器的耦合系数和外部品质因子进行计算,以高效的得到符合设计要求的电路版图。谐振器间的间距由耦合系数来确定,馈线的布局由外部品质因子来确定。耦合系数Mij和外部品质因子Qex的计算公式分别为式(4)和式(5)。其中,fp1和fp2是两个谐振器在弱耦合下的耦合低频率和高频率,f0为S11响应的峰值频率,Δf±90°是S11相位曲线正负90度对应的频差。根据计算的Mij和Qex可以对滤波器的优化提供理论指导。

(4)

(5)

下面以传输线理论对陷波的形成开展分析。陷波单元谐振时会与多模谐振器的通带产生耦合作用,而与多模谐振器及其馈电网络组成新的滤波器系统。当陷波单元处于非谐振状态时,不参与滤波器的传输响应。仿真和实测结果也表明,陷波单元的加入对滤波器通带响应的影响并不明显。因此,为理解陷波单元的工作原理,将陷波单元视作带通滤波器的负载来分析,如图2所示。

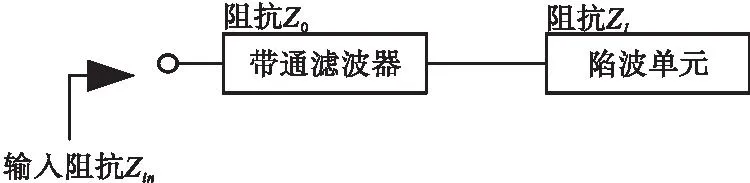
图2 陷波单元作为带通滤波器负载的拓扑图Fig.2 The diagram of notched resonator is regarded as load for bandpass filter

根据传输线理论可以得到输入阻抗Zin为式(6)所列:

(6)

式(6)中,Z0为带通滤波器传输响应时的特征阻抗,Zl为陷波单元的特征阻抗,θ表示频率的电长度。

当处于通带响应时,负载不参与滤波器传输响应,此时等效于没有负载,输入阻抗Zin为式(7)所列:

Zin=jZ0tanθ

(7)

当处于陷波响应时,负载为谐振状态,即Zl=∞,此时输入阻抗Zin为式(8)所列:

(8)

无论是陷波响应还是通带响应,多模谐振器均表征为谐振状态,对式(7-8)进行化简,即有式(9):

(9)

因此,只要将一个具备带内谐振特性的负载以一定的耦合关系加载到一个带通滤波器上,就可以在通带内产生陷波响应,这为陷波滤波器的设计提供了理论指导。本文介绍的高温超导陷波滤波器均是在该理论指导下开展的研究和设计。

2 多模谐振器设计与分析

高温超导滤波器工作环境对低温的要求非常苛刻,为了降低制造和维护成本,要求高温超导微波无源器件进行小型化设计以节约空间,其中采用多模谐振器是设计小型化滤波器的一种有效方法。本文介绍两款团队提出的多模谐振器,并对其谐振特性进行分析。

2.1 非对称双T型加载的多模谐振器

为了满足宽带和小型化需求,团队提出了非对称双T型枝节加载的多模谐振器,并采用经典的奇偶模分析方法对谐振器谐振特性进行分析,如图3所示,为了便于分析,将其中心对称线分别设置为电壁和磁壁,就分别得到了奇模电路和偶模电路,如图3(b)和图3(c)所示,其中W是宽度;L是长度。

图3 非对称双T型加载的多模谐振器和奇偶模电路Fig.3 Proposed multi-mode resonator loaded asymmetric double T-shaped stubs and equivalent circuit models

根据传输线理论,可得到奇模的输入导纳为:

Yin_odd=-jY1cotθ1

(10)

奇模在输入导纳为零时产生谐振,可以得到奇模谐振条件为式(11)所列:

cotθ1=0

(11)

根据式(11),奇模谐振频率完全由枝节L1进行控制。对于图3(c)所示的偶模,输入导纳为式(12)所列:

(12)

通过化简,并假设Y1=Y2,得到偶模谐振条件为式(13)所列:

tanθ1+tan(θ2+θ3)+tan(θ4+θ5)=0

(13)

根据式(11)和式(13),可设计具备三模特性的多模谐振器,谐振特性和电流分布如图4所示。谐振器偶模由加载枝节L3和L5控制,如图5所示。

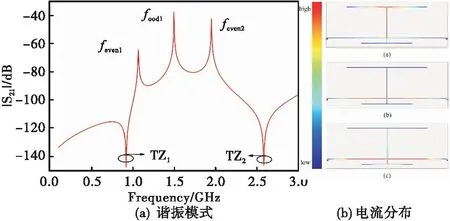
图4 多模谐振器的谐振模式和电流分布Fig.4 Resonant frequencies of the proposed multi-mode resonator and current distributions at resonant frequencies

图5 频率与枝节长度的关系Fig.5 Resonant frequencies with varied stub lengths

2.2 双阶跃阻抗多模谐振器

团队在经典发卡谐振器的基础上,通过不均匀阻抗分布技术和去耦合技术,提出了双阶跃阻抗双模谐振器[16]如图6所示,谐振模式电流分布图见图7。由于该谐振器为对称结构,为便于分析,将其中心对称线分别设置为电壁和磁壁,如图6(b)所示,就分别得到了奇模谐振电路和偶模谐振电路,如图6(c)和(e)所示。在奇模谐振电路中,根据谐振原理,(Z3,θ3)传输线对奇模谐振无影响,因此奇模谐振电路可化简为图6(d)。

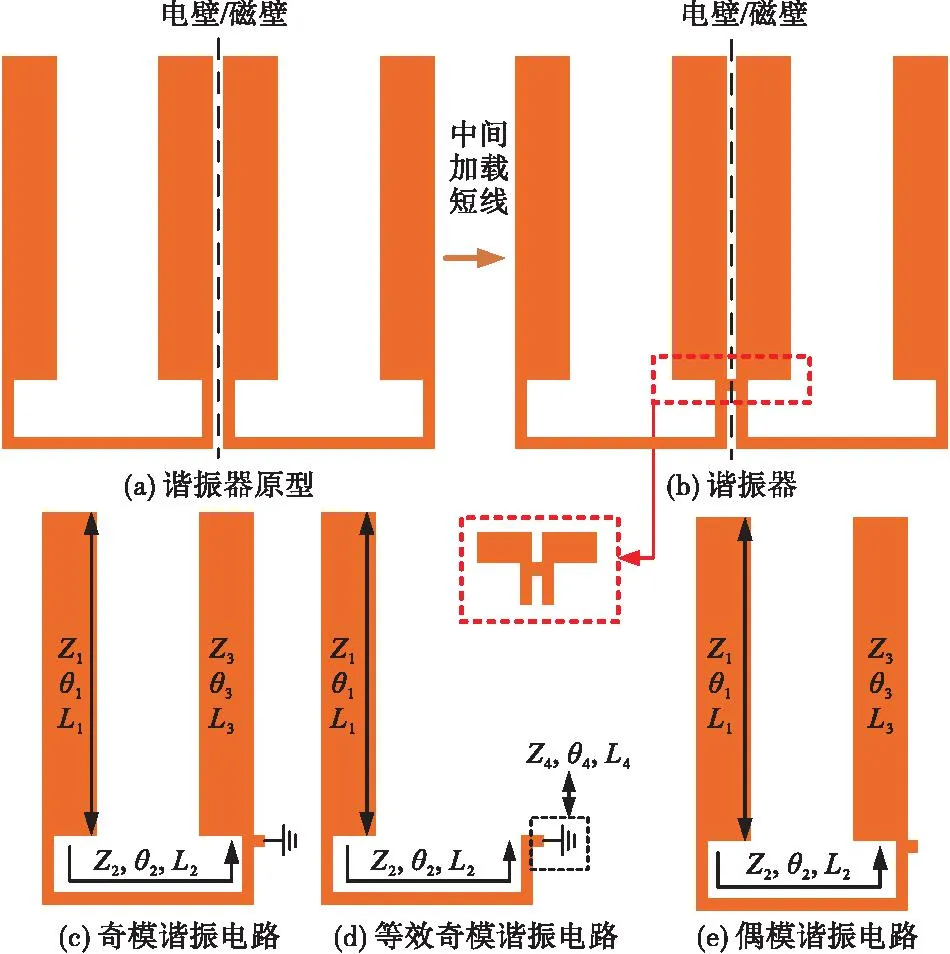
图6 团队提出的双阶跃阻抗谐振器Fig.6 Proposed double stepped-impedance resonator

图7 谐振模式电流图Fig.7 Current distributions at resonant frequencies

根据传输线理论和奇偶模理论,可以计算出谐振电路的奇模输入导纳Yin-odd和偶模输入导纳Yin-even分别为式(14)与式(15)所列:

(14)

(15)

根据谐振时的输入导纳为零的原则,并通过简化和计算,可以得到奇模谐振频率fin_odd和偶模谐振频率fin_even分别为式(16)与式(17)所列:

(16)

(17)

其中,εe1、εe2和εe3分别是(Z1,θ1),(Z2,θ2)和(Z3,θ3)传输线的有效介电常数。从式(16-17)可得偶模谐振频率可通过电长度θ3进行独立调控,而不改变奇模谐振频率。

3 高温超导陷波滤波器设计

新疆天文台的25米射电天文望远镜工作波段之一为L波段,但在该波段受到GPS信号和地面移动通信信号的严重干扰,影响了其性能和相关科学工作的开展。考虑到宽带特性、低温空间的小体积以及干扰信号的抑制,恢复已被干扰的射电天文望远镜的探测能力,团队基于宽带特性和小型化需求,提出一款新型非对称双T型枝节加载的多模谐振器,并在陷波形成的理论指导下,设计了两款高温超导单陷波宽带滤波器和一款高温超导双陷波宽带滤波器。设计的高温超导陷波宽带滤波器采用的介质基板均为氧化镁(MgO),介电常数为9.78,基板厚度为0.5mm,电路加工后均在77K低温条件下进行测试。团队设计的单陷波宽带滤波器在新疆天文台25米射电天文望远镜的干扰场景中进行了试用,结果显示,设计的陷波滤波器具备明显的电磁抗干扰能力。

本部分内容介绍的前两款滤波器均采用非对称双T型枝节加载的多模谐振器设计,合适的耦合产生了优异带内波纹的宽带响应,内嵌弯折陷波单元实现了窄带陷波响应,源负载耦合方式获得了零点响应以提高通带选择性。最后一款滤波器采用双阶跃阻抗谐振器设计,借助阶跃阻抗谐振器特性产生了宽阻带的响应,下面具体介绍。

3.1 单陷波宽带滤波器

该滤波器拓扑图和实物图见图8,尺寸大小为0.318λg×0.247λg。仿真和实测结果见图9,带宽为1GHz～2GHz,相对带宽为66.7%,插损优于0.2dB,回波损耗优于19dB。弯折馈线和耦合产生了一对传输零点提高了通带选择性,阻带抑制度为20dB。陷波位于1.805GHz,相对带宽为0.56%,抑制度为25dB[2]。团队将图8所示的滤波器进行了拓扑结构的改变,进而开展了尺寸小型化和稍宽陷波带宽的设计工作[3],此工作本文不再赘述。

图8 单陷波高温超导滤波器拓扑图和实物图Fig.8 Layout and photograph of the proposed wideband HTS filter with a narrow notched-band

图9 单陷波高温超导滤波器仿真与实测S参数响应Fig.9 Simulated and measured S-parameters responses of the fabricated wideband HTS BPF with a narrow notched-band

3.2 双陷波宽带滤波器

为了抑制L波段内的GPS L1频段和1.8GHz地面移动通信频段的干扰,团队在上述工作[2-3]的基础上开展了高温超导双陷波宽带滤波器的研究和设计。该滤波器拓扑图和实物图如图10所示,陷波频率可由枝节L15和L17分别调控。仿真和实测结果见图11,带宽范围为1GHz～2GHz,插损优于0.47dB,由于加工误差,仿真结果为22dB的回波损耗实测为14dB。由弯折馈线和耦合产生了五个传输零点(transmission zero,TZ),将阻带抑制度改善到20dB以上,通带矩形系数(BW-40dB/BW-3dB)为1.2,具备很好的通带选择性。陷波位于1.575GHz和1.82GHz,相对带宽为0.56%和0.54%,抑制度均达到了30dB,可以很好地对干扰信号进行抑制。

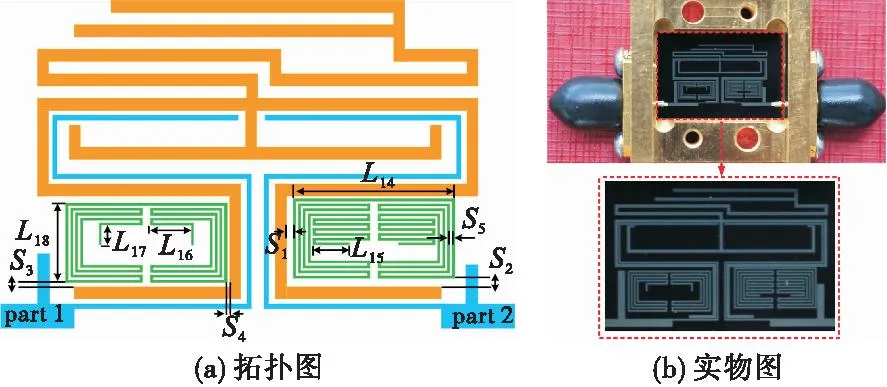
图10 提出的双陷波高温超导宽带滤波器拓扑图和实物图,Fig.10 The fabricated wideband HTS filter with two notched-band

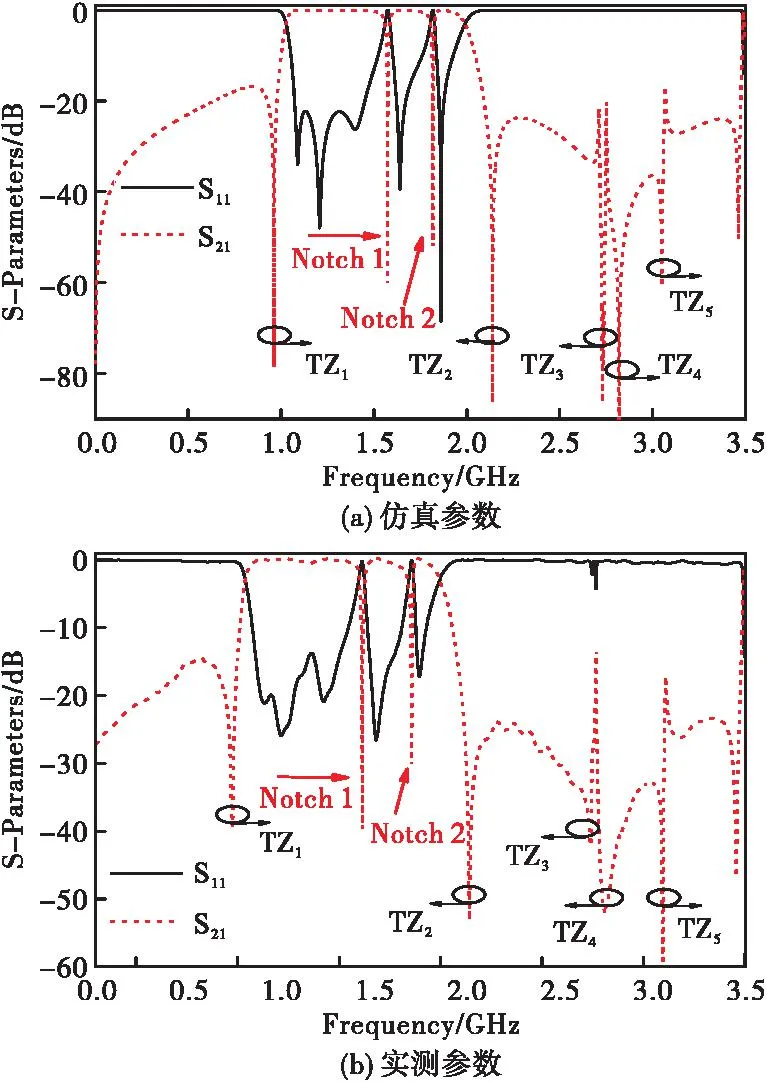
图11 双陷波高温超导滤波器的仿真和实测S参数Fig.11 Simulated and measured S-parameters responses of the fabricated wideband HTS BPF with two narrow notched-band

3.3 单陷波多通带滤波器

为满足射电天文望远镜同时对多个射电源信号的独立接收需求,并对通带内的1.8GHz地面移动通信信号干扰的抑制,团队基于双阶跃阻抗双模谐振器开展了高温超导单陷波多通带滤波器的研究和设计。

陷波单元的耦合强度可以调控陷波相对带宽,其电长度可以调控陷波频率。整个陷波滤波器的拓扑结构和S参数响应如图12和图13所示。

图12 高温超导单陷波多通带滤波器拓扑图Fig.12 Layout of the HTS filter with a narrow notched-band and multi-bandpass

图13 S参数响应Fig.13 S-parameters responses

陷波单元与主谐振器间的耦合关系产生了一对传输零点,获得了很好的陷波特性。同时,两个通带因耦合关系各产生了一个传输极点,这一特性不仅增强了陷波的衰减特性,同时增强了通带的选择特性。陷波滤波器三个通带的中心频率分别为1.775GHz、1.89GHz和2.45GHz,通带相对带宽分别为3.49%、3.09%和3.47%。陷波的中心频率为1.83GHz,相对带宽为3.06%,陷波抑制度达到27dB,阻带倍频程以抑制度为23dB延展至3.94fodd[16]。其宽阻带产生的机理为:阶跃阻抗谐振器由于其阻抗分布的不均匀性产生了有效介电常数改变的结果,根据谐振原理,进而其谐振器本身具备将高次谐波推高至离基模更远的频率处的能力,同时该滤波器设计的馈电方式对谐振器高次谐波的激励较弱,特别是偶模的二次和三次谐波没有被有效激励,使得设计的滤波器阻带较宽,可以延展至近4倍频处,获得了较好的宽阻带效果。

4 结论

本文介绍了研究团队近年在具备电磁抗干扰能力的高温超导陷波滤波器和射电天文应用方面的研究工作,介绍了基于非对称双T型枝节加载和双阶跃阻抗的多模谐振结构在宽频带和多频带小型化的陷波滤波器中的研究和设计。相较于普通材料,高温超导材料能够有效地减少插入损耗,进而提高射频前端的灵敏度,增强接收系统对微弱电磁信号的探测。同时,陷波的设计能够很好地抑制接收频段内的电磁干扰,提升系统的抗干扰能力。因此,本文的研究工作在电磁环境复杂恶化的现代和未来射电天文以及深空探测的电磁抗干扰和高灵敏度系统中具有一定的应用前景。下一步,随着科学研究需求和无线电通信系统的增多,基于宽带单/双陷波和多频带单陷波的工作,将开展多频带多陷波技术的研究和应用,以适应不断复杂变化的电磁环境和应用需求。