基于卷积神经网络的雷达辐射源稳健识别方法
2024-01-12郭林昱杨新权
郭林昱,杨新权,匡 银,文 伟
(中国空间技术研究院西安分院,西安 710000)
0 引言
雷达技术发展迅速.新的雷达信号调制技术不断涌现,新体制雷达逐渐取代了传统的常规脉冲雷达,更多的信号类别被投入使用[1],这一改变使雷达所处电磁环境愈加复杂,也提高了雷达信号识别难度[2]。当前多功能雷达普遍采用复杂调制类型,使得收到的信号具有“低-零”功率特点[3],接收信号信噪比低,因此如何在低信噪比下对雷达辐射源信号进行高效识别成为了亟待解决的问题。
雷达辐射源信号的识别问题从数学角度上分析可以看作是一个模式分类的问题[4],针对雷达信号识别问题,可以进一步的分为特征选择和分类器选择两大部分。传统的识别方法普遍依赖脉间参数,通过将其与数据库进行比对,从而得到相关雷达信息。随着雷达技术的发展,信号复杂程度以及电磁环境复杂程度日益增加,因此研究者们选择的特征已经从传统的脉间特征转向了脉内特征[5],而在分类器的选择问题上,鉴于深度神经网络对于大量数据具有更好的处理能力,各种神经网络逐渐取代了决策树等传统方法,这被广泛地运用于雷达信号的分类问题[6]。
目前针对雷达辐射源信号特征的提取方法主要包括时频分析法[7]、模糊函数法[8]、高阶统计量法[9]等,其中时频分析法运用最为普遍。黄智等[10]利用Choi-William分布得出信号时频特征图,并结合卷积神经网络(convolutional neural network,CNN)进行分类,得到了较好的识别准确率。全大英等[11]基于多重同步压缩变换(multis ynchrosqueezing transform,MSST)及方向梯度直方图(histogram of oriented gradient,HOG)特征提取,利用主成分分析法(principal component analysis,PCA)结合支持向量机的方法完成了识别任务,识别准确率较高。普运伟等[12]利用模糊函数主脊坐标变换结合卷积神经网络完成雷达辐射源信号识别,在识别准确率和鲁棒性上都有一定的提升,但以上基于时频变换的方法普遍存在预处理复杂、耗时长的问题。王学忠[13]通过小波变换结合CNN的方法,利用多特征融合完成了对于雷达信号的识别,该方法识别准确率较高且增强了识别系统的鲁棒性。李红光等[14]针对跳频信号的识别问题,提出了一种基于时频能量谱纹理特征的识别方法,利用支持向量机对特征集进行训练、分类和识别,得到了较好的识别准确率。
目前研究者们要获得所选用的特征,都需要对信号进行一些相对复杂的变换处理,而这样的处理在增加耗时的同时也可能会带来一些信息的丢失。
针对特征提取复杂耗时长且损失信息多的问题,考虑到雷达信号主要的调制方法是调频和调相,而这类调制信息均可以通过相位变化特性得到完整的体现,为避免复杂特征提取带来的时间资源消耗,本文选择相位作为特征。 其不仅包含几乎全部的调制信息,且提取较为简单,因此具有较强的可用性。
因相位特征对于噪声较为敏感[15],而PCA[16]具有降噪的特点,因此为保证低信噪比下的识别性能,针对相位特征,我们采用PCA作为降噪手段。与此同时,PCA的降维能力也大大缩短了耗时,提升了模型对噪声的稳健性。在分类器的选择上,鉴于CNN[17]利用局部连接和权值共享很大程度上减少了网络中参数个数,有效缓解了模型过拟合问题,因此本文选择结构较为简单且分类能力强的CNN网络作为分类器。
本文引言部分介绍了雷达辐射源信号识别的研究现状,第一章介绍了本文所采用的特征提取方法、PCA原理以及CNN结构,第二章给出了具体实验及参数设置,第三章对比分析了几种不同方法的实验结果,最后一章对本文提出方法进行总结并确定进一步的研究方向。
1 基于相位特征与PCA的雷达辐射源信号识别算法
本文所提出方法流程如图1所示。
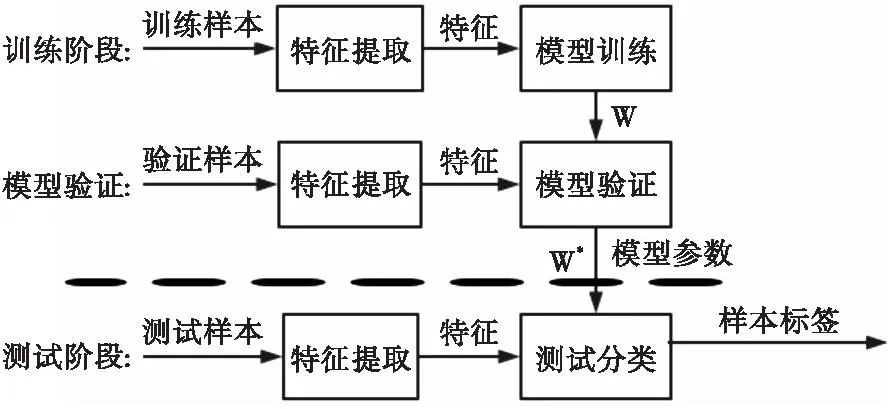
图1 本文所提出的方法流程图Fig.1 Method flow chart of this paper
本文所提出的方法处理流程可分为训练和测试两个阶段,其中训练阶段又包括训练和验证两部分。在3个部分里首先都需要对样本进行特征提取,在特征提取阶段,本文所提方法采用瞬时相位作为特征进行识别,更进一步地,为了降低噪声的影响,本文引入主成分分析法对噪声进行抑制;而后将处理过的相位特征送入卷积神经网络对模型进行训练。在训练阶段,训练好的模型首先需要利用验证集进行验证从而调整优化模型参数;最后在测试阶段利用训练好的模型进行分类,输出样本标签,即可得到分类结果。
1.1 特征提取
在特征提取上一般要遵循一些规则[18],尽可能选择区分度高的特征,传统的特征多选择以经典五参数为主的脉间特征,后改进为使用双谱、时频能量分布[19]、熵特征[20]等各种脉内特征。在特征提取上,因相位特征是脉内调制特性的直接反映,本文选择相位作为特征进行雷达辐射源信号的识别。
根据调制方式的不同,各类雷达信号表示如下[21]。
常规脉冲信号如式(1)所列。
(1)
式(1)中a为振幅编码序列,fc为载波频率,θ为相位,T为脉冲宽度。
其相位如式(2)所列。
θ(t)=2πf0t+φ
(2)
相位编码如式(3)所列。
(3)
式(2)式(3)中θ(t)为相位调制函数,u1(t)为矩形脉冲,T为脉宽,针对相位编码信号,此处采用了二项编码和四项编码两种信号。其中,二相编码的θ(t)取值为0或π,四相编码的θ(t)取值为0,π/2,π或3π/2。
线性调频如式(4)所列。
(4)
式(4)中,T为信号的脉冲宽度,K=B/T为调频斜率,f0为中心频率。
非线性调频如式(5)所列。
(5)
此处相位θ不同,则信号不同。
频率编码信号如式(6)所列。
(6)
式(6)中,fi∈{f1,f2,…,fM},M为频率数量,编码码元数量为N,码元宽度为Tp。
复杂调制:
此处采用的是调频和调相相结合的混合调制,因此考虑在式(6)的基础上对于相位部分进行调制,相位表示如式(7)所列。
(7)
基于不同类型信号的相位存在差异可知,相比于其他特征,相位特征具有如下优点:
(1)特征提取快速;
(2)相位信息是频率、相位的完整反应,无信息丢失。
1.2 主成分分析法
PCA作为一种数据分析技术被广泛运用,其核心思想是通过对复杂的高维数据进行投影,将其映射到低维空间,筛选出数据中的主要成分,而被舍弃的残余分量主要为噪声分量,因而其具有降维去噪的能力[22]。
(8)
样本方差如式(9)所列。
(9)
协方差矩阵如式(10)所列。
(10)
式(10)中的C是列方差沿着对角线排列的协方差矩阵,对其进行特征值分解得到如式(11)所列。
C=Q∑Q-1
(11)
式(11)中,Q是矩阵C的一组正交单位化后的特征向量,∑是一个对角阵,对角线上的元素即为C的特征值,如式(12)所列。
(12)
式(12)中,λ1≥…λi≥λi+1≥…≥λN,若所要求保留的维数为a,则选择其中前a个特征值对应的特征向量作为主成分。
1.3 卷积神经网络
CNN由输入层、卷积层、激活函数、池化层以及全连接层和输出层组成,CNN网络结构如图2所示。
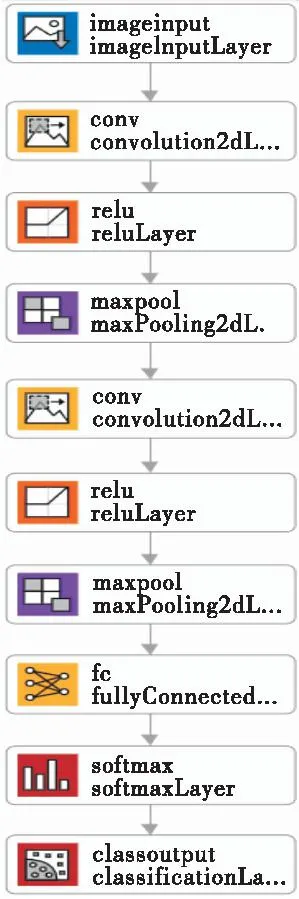
图2 CNN结构图Fig.2 The CNN structure
输入层和输出层用于数据的输入输出,而在卷积神经网络中,其核心是卷积层,卷积层本质上可以看作是一个特征提取器,用于自动提取输入信号的深层信息,如式(13)所列。
(13)
式(13)中,f(·)为激活函数,bj代表偏置值,ωij为卷积核,Yj为第j个神经元输入,l表示层数。
在激活函数的选择问题上,常用的激活函数包括sigmoid和tanh和Relu等等,而其中Relu是最为常用的激活函数,如式(14)所列。
f(x)=max(0,x)
(14)
池化层的作用是对激活函数输出的新特征量进行降维,从而减少运算复杂度,加快计算速度,具体如式(15)所列。
(15)
式(15)中,βj为乘性偏置,bj为加性偏置,d表示池化函数,在池化过程中,较为常用的池化方法是最大池化和平均池化。
全连接层被用于局部特征组合和特征分类,将每一个节点都与上一层的各个节点相连,从而将前边提取到的特征综合起来[23]。
2 仿真实验
本文仿真实验基于MATLAB2022b版本进行,计算机CPU主频为2.3GHz,选择常规脉冲信号,二相编码信号,线性调频信号,非线性调频信号,四相编码信号和频率编码信号6种典型信号以及线性调频结合相位调制的复杂调制信号共7种信号进行仿真。在-5dB~10dB的情况下以1dB为步长,在10dB~20dB区间以2dB为步长,在-5dB~20dB的信噪比下,各类信号分别产生350个样本信号和100个测试信号作为训练集和测试集,另有50个采样信号作为验证集,每一信号类型的每一样本包含400个采样点。对样本信号采用上述特征提取方法,先提取样本信号的相位,然后采用PCA对其进行降维,最后将数据输入卷积神经网络进行训练识别。
PCA维度的选择对识别性能有较大的影响,在选择特征维度时,通常以能量重构比例作为标准[24-25],选择特征维度为能量保留95%,其对应的特征维数为88维。本文构造一个10层的CNN网络作为分类器,其中包括1个输入层, 2个卷积层,2个池化层,2个非线性激活层, 1个全连接层,1个激活函数和1个输出层。其中,1个卷积层—relu—池化层结构可以看作是一个小的特征提取单元,通过将这样的小单元进行叠加可以提升网络性能,此处使用的网络大小包含两个这样的特征提取组合,卷积核个数分别是4和2,卷积核大小分别为1*5和1*3,池化层核大小均为1*3,步长均为2,池化方式为最大池化。
基于以上,为进一步对比分析本文所采用方法的性能,分别利用较为经典的小波变换[26]、能量谱密度[14]以及直接使用相位作为特征,结合卷积神经网络进行识别,其结果如图3所示。
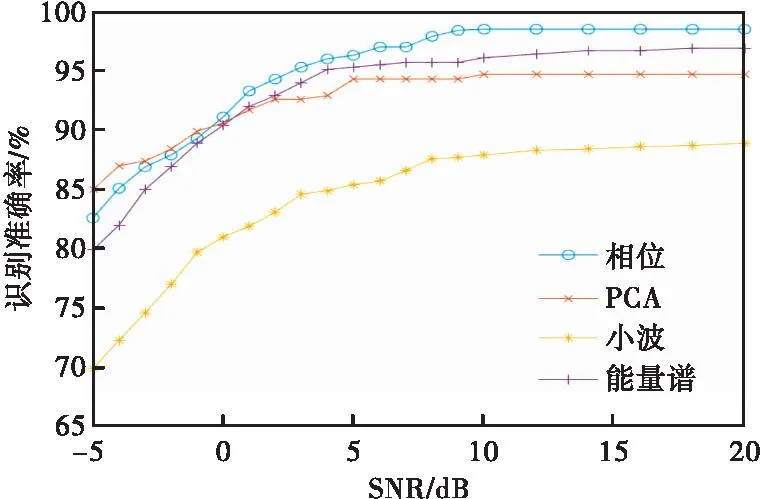
图3 不同信噪比下的各方法识别准确率对比图Fig.3 Comparison of recognize accuracy of different methods under different SNR
如表1所列为各方法的训练时长、预处理耗时和识别时间对比。

表1 各方法的耗时对比表Tab.1 Time comparison table of each method
3 实验结果分析
从图3中可以看出以上4种方法的识别准确率都随着信噪比的提升而提升。小波变换法在各个信噪比下的识别准确率明显低于其他3种方法,且预处理时间是本文所提出方法的数倍。而其他的3种方法性能较为相近,在0dB以下,基于能量谱密度的方法识别准确率低于基于相位的两种方法,而0dB以上能量谱密度作为特征的方法性能略高于本文提出方法,但是低于相位直接作为特征的方法,且数据预处理时间同样远超以相位作为特征的方法和本文提出的方法。
本文提出的方法是在基于相位特征法上的改进,因此我们首先针对没有引入PCA的3种方法进行对比,通过观察曲线图可以发现,基于相位特征的方法整体高于其他两种方法。在信噪比高于0dB时,基于相位特征的方法识别准确率即可保持在90%以上,在信噪比高于3dB时,即可保持在95%以上,可以证明相位特征在信号识别中的有效性。
进一步观察基于相位特征的两种方法,在0dB以上时,引入了PCA的方法相比于直接选择相位作为特征的方法识别性能有小幅度下降,但都保持在90%以上。而在0dB以下时,本文方法的识别准确率明显高于其他3种方法,保持在85%以上。这是因为在确定PCA的保留维度时,是以固定的能量比为标准,在低信噪比的情况下,PCA去除的分量主要是噪声,而在高信噪比下,噪声能量占比小,损失了部分信号能量,因而识别性能略有降低。
为保证实验结果的可靠性,本文进一步对所采用的CNN模型进行了消融实验以避免模型过拟合问题,将本文所用网络和进行网络缩减后的网络在各信噪比下的识别准确率进行对比,其结果如图4所示。
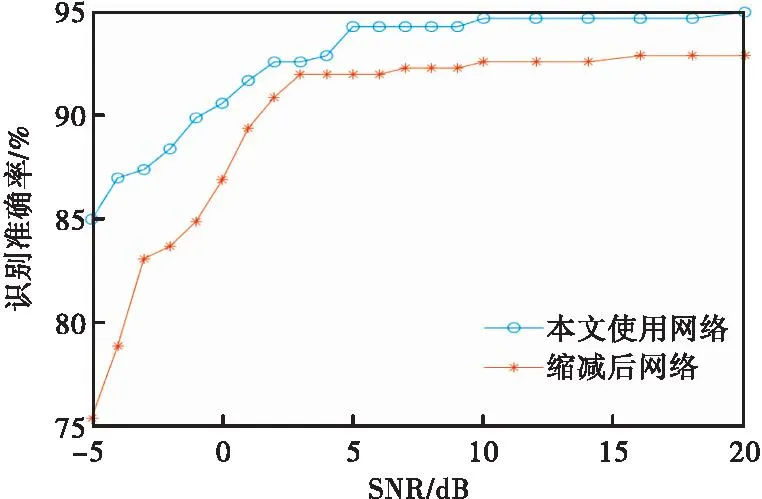
图4 不同信噪比下的当前网络和缩减后网络的识别准确率对比图Fig.4 Comparison of recognition accuracy of the current network and the reduced network under different SNR
在同样的数据输入情况下,缩小了网络规模,识别性能明显下降,且在当前网络下的验证集识别准确率和测试集识别准确率的结果基本一致,即可表明当前的网络并不存在过拟合问题。
本文提出的方法表现出随着信噪比降低性能损失较小的特点,因利用PCA可以达到降噪的效果,使得本文方法具有良好的噪声稳健性,同时PCA的降维作用使得训练时间和识别时间都明显缩短,并且网络的参数量和计算量也得到大大缩减,各方法参数量和计算量如表2所列。
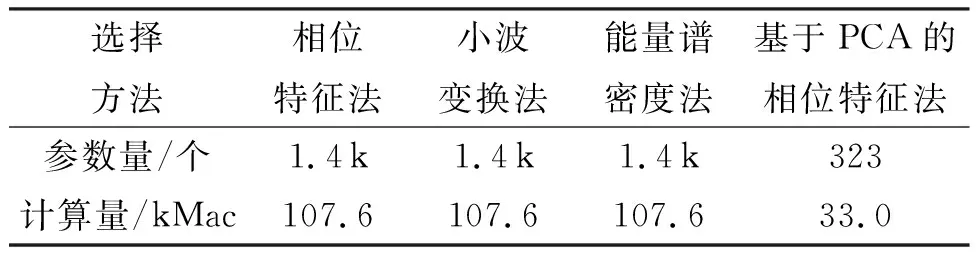
表2 各方法的参数量及计算量对比表Tab.2 Comparison table of parameters and calculation amount of each method
而在耗时和运算复杂度的问题上,本文从特征提取和降维两方面进行优化,避免了复杂的特征提取,降低了运算复杂度,缩减了耗时;另外通过PCA的降维,大幅度的缩减了所需要处理的数据规模。综合两点,本文所提方法在耗时和计算量上体现出来了较为明显的优势。
4 结论与展望
本文所提出的方法识别性能随着信噪比降低,性能损失较小,具有良好的噪声稳健性;大幅减少了运算复杂度,耗时较短;利于在星载平台等资源受限平台上部署,具有较好的工程应用前景。
在本文所提出的背景下,需要进一步的提高识别的准确率,后续对于当前使用的网络模型可以进行进一步研究,对卷积神经网络结构进行优化调整,提升网络对不同信号识别的适应能力和鲁棒性,使网络可以更加适应雷达辐射源信号分类问题。
