迁移深度神经网络的页岩总孔隙度预测

汪 敏 ，杨 桃，唐洪明，闫建平，廖纪佳

1.西南石油大学电气信息学院，四川 成都 610500 2.油气藏地质及开发工程全国重点实验室·西南石油大学 四川 成都 610500 3.西南石油大学地球科学与技术学院，四川 成都 610500

引言

页岩气的赋存方式与常规天然气有极大的差异，对于其赋存原理及勘探开发的研究是当下石油天然气工业的热点问题。孔隙度作为页岩储层评价的关键参数之一，对其定量研究十分必要。孔隙度的准确值只有通过岩芯分析得到，但是，岩芯的获取成本极高。而且，页岩孔隙一般以纳米为主[1-3]，常规的储层孔隙研究方法很难应用于页岩孔隙度的表征预测[4-6]。为了降低取芯的成本，亟需新的方法来达到这一目标。

针对这一问题，国内外众多学者进行了一系列研究。其中，Luffel 等[7]根据核磁共振测井资料计算得到孔隙度，但是在计算过程中，没有将储层含气状态考虑在内，含气饱和度必须以获得的地层真实孔隙度为基础计算得到。因此，用单一的核磁共振测井资料计算得到的孔隙度很难保证准确度[8]。钟光海等[9]直接利用测井曲线表征页岩孔隙度，通过多次实验，优选出声波、密度、铀含量和岩芯孔隙度，建立了孔隙度预测模型。该方法存在两方面的不足：一方面，这种方法需要很多数据进行拟合，模型参数与测井数据密切相关；另一方面，模型表征性能随井深而变化。近些年来，人工智能技术在各方面都取得了令人瞩目的成就，将人工智能应用于储层关键参数预测及其评价也已经成为石油和天然气工业的一大趋势，已经有诸多应用[10-13]。杨柳青等[14]利用密度、声波、自然伽马和泥质含量作为输入参数，利用深度学习技术训练卷积神经网络（Convolutional Neural Network，CNN）对储层孔隙度进行预测。该方法可以准确地预测储层孔隙度。但是，卷积神经网络需要大量的有标签测井数据，在实际工程中很难在每一口井上都获得足量可以很好地用于训练深度学习网络的测井数据，尤其是岩芯数据。对于地质的非均质性，存在两个问题：1）还没有一个定量的指标来对其进行衡量；2）在此情况下，用一口井的测井数据训练的深度神经网络模型可能不再适合邻井的储层情况。

针对上述的一系列问题，提出一种全新的机器学习理念 深度迁移学习，并基于该理念构建全新的页岩孔隙度预测模型。首先，使用皮尔逊相关系数法优选出适合深度神经网络的测井参数作为输入，训练得到可以很好地预测该井的深度神经网络模型。然后，提出最大均值差异（Maximum Mean Difference，MMD）衡量源井（有大量较好测井数据的井）和目标井（只有少量测井数据的井）测井数据分布的相似性，为后续迁移深度神经网络性能提供依据。最后，以源井的深度神经网络作为预训练网络，在目标井上用少量的数据加以微调，得到预测目标井储层孔隙度的迁移深度神经网络（Porosity Transfer Deep Neural Network，PTDNN）模型。通过测试对比，在B2 井上只使用了200 个（为预训练网络训练数据需求量的10%）测井数据和对应的岩芯孔隙度数据就训练得到了预测性能很好的迁移深度神经网络。

本文主要贡献为：1）建立全新孔隙度预测的迁移深度神经网络模型，充分利用历史测井数据，使用少量新的测井和岩芯数据实现较高精度的孔隙度预测。该方法克服了一般深度学习网络需要大量测井数据训练模型，尤其是对于岩芯数据的依赖。同时，也获得了深度学习优异的预测性能，达到了极大降低测井解释成本的效果。2）提出MMD 来定量衡量两口井之间的差异，为两井间地质差异提供了一种评价依据。

1 地质概况

长宁国家级页岩气开发示范区位于四川盆地南部的宜宾市和泸州市，东西横跨90 km，南北达40 km，其区块面积约为2 050 km2（图1）。目前，区域内已钻获页岩气井超过240 口，为国家页岩气开发研究提供了基础条件。

图1 研究区位图Fig.1 Research location map

四川盆地位于亚洲大陆东南，盆地呈NE—SW向走势，是多次构造运动的结果。背斜顶部为寒武系—志留系，其两翼为二叠系－三叠系。长宁地区继承了四川盆地地质演化特征，大部分为二叠系—三叠系—侏罗系，总体走向是NW—SE向[15]。该地区在大面积低能、缺氧及欠补偿沉积地质环境下形成了大量的低渗透率、低孔隙度及高有机质的页岩储层[16]。研究资料显示，长宁地区的主要储层为五峰组－龙马溪组，发育有大量黑色页岩，厚度为214.5～450.5 m。龙马溪组储层分布稳定，埋藏深度浅，一般在1 700～3 500 m，总有机碳含量低。

本文研究的A1、A2、B1、B2 的4 口井均位于长宁中奥顶构造南翼，都为3 500 m 以浅的测试井。其主力储层——龙马溪组由龙一段和五峰组组成，龙一段又由4 个小层（龙一1，龙一2，龙一3，龙一4）组成。

测井数据文件包含详尽的工程数据，例如，声波时差、井径、补偿中子、自然伽马、铀和光电吸收截面指数等众多的测井数据。并且这4 口井都进行了钻井取芯工作，由此，可以分析得到准确的页岩孔隙度值。

2 孔隙度预测的迁移深度神经网络模型构建

首先，提出迁移深度神经网络模型的理论基础；然后，在理论的基础上，以长宁地区4 口井的测井及岩芯孔隙度数据构建目标井的孔隙度预测迁移深度神经网络模型。

2.1 迁移深度神经网络模型理论

迁移深度神经网络（Transfer Deep Neural Network，TDNN）的构建过程，由初始训练模型以及在此基础之上再训练得到的迁移网络两步组成。

2.1.1 初始训练模型

深度神经网络（Deep Neural Network，DNN）是由一层层神经元组成的，神经网络一般包括输入层、隐藏层和输出层（图2）[17]。深度神经网络是指层数超过3 层的神经网络，其强大的非线性拟合能力使得其成为解决各种复杂非线性映射问题的首选方法，成为深度学习的基础。

图2 神经网络的结构Fig.2 The structure of the neural network

神经网络的训练过程由两个过程组成，分别为前向传播和反向传播。前向传播过程中，给定权值和偏置矩阵，通过各神经元节点运算处理得到输出的预测值。在反向传播过程中，通过损失函数对权重系数ω 和偏置系数b求导而不断更新这两者的值，从而使得网络不断地减小预测值与实际值的误差，直至找到最合适的权值和偏置让损失函数收敛。

1）前向传播过程

对于第j层第l个神经元节点输入值

写为向量形式

式中：ω—权重系数；

b—偏置系数；

k－前一层（j-1）神经元节点数目；

a－输入向量；

b－偏置系数向量；

z—激活函数ReLU 的输入向量；

σ()—ReLU 激活函数，其形式为

2）反向传播过程

反向传播考察的是权重和偏置如何影响代价函数，其具体的含义为：计算，从而不断修正权重和偏置使得损失（代价）函数c不断减小直至收敛。

通过链式法则求导，最终得到

优化器决定反向传播过程中参数更新的方式，对于模型的性能有着决定性影响。在本文中选用RMSprop 作为模型优化器。RMSprop 是一种自适应优化器，它会对累积平方梯度添加一个衰减系数，尽可能地避免梯度陷入局部极小值。

对于回归（预测）类问题，常选择均方误差（Mean Square Error，MSE）作为损失（代价）函数，均方误差指的是参数估计值与参数真实值yi之差平方的期望值，它的形式为

式中：L1均方误差；

n－数据个数。

2.1.2 迁移深度神经网络模型

深度学习有卓越的预测和分类能力。但是，其优异性能基于大量的有标签数据。然而，现实中难以获得足量并且高质量标注的数据，例如，岩芯数据。这一瓶颈严重制约深度学习的应用[18-20]，迁移学习可以成功地解决这一问题。将迁移学习应用于孔隙度预测构建迁移深度神经网络就可以用少量数据达到优异的性能。

但是，迁移学习的性能和源域数据与目标域数据分布的相似性密切相关。源域数据与目标域数据分布越相似，迁移学习所得的模型在目标域上表现越好，相反，源域数据与目标域数据分布差距过大，则会出现负迁移。因此，定量地衡量源域数据与目标域数据间的分布相似性是一项十分必要的工作。

源域有大量有标签数据Ds={(x1,l1),(x2,l2),···,(xn,ln)}，而目标域上只有少量数据有标签或者全部无标签Dt={(xt1,lt1),(xt2,lt2),···,(xt(n-1)),(xtn)}。在本文中，源域就是有大量测井数据的井，而目标域是只有少量测井数据的井。

使用最大均值差异来衡量源域数据与目标域数据分布的相似性。迄今为止，还没有一个定量的指标衡量井间的非均质性差异，这一概念可以很好地解决这个问题。在统计学中，当两个数据分布不同时，应该用使两个分布之间差距最大的那个距离来作为度量两个分布的衡量。MMD 正是来源于这一思想，假设存在两个分布p和q，利用核函数将两分布映射到无穷维的高维空间，然后再求两者的期望差值，当在某映射关系下两者期望差值取得最大值时，此时就是最大均值差异，用于衡量两个分布的相似性。最大均值差异为

式中：D－最大均值差异；

F原始数据映射到再生核希尔伯特空间的函数集合；

f—F中的一个映射函数；

Ep,Eq—求取均值的函数。

在实际应用中，常用最大均值差异的经验估计值进行计算，设源域和目标域对应p,q，两数据分布映射到再生核希尔伯特空间为`p,`q，各自含有m和n个数据，则最大均值差异的经验估计值D′为

最大均值差异衡量源域与目标域分布相似性，可以为迁移学习性能差异提供解释。同时，最大均值差异可以定量衡量源井和目标井间的非均质性差异大小。在计算源域和目标域间最大均值差异后，就可以在预训练网络的基础上构建迁移深度神经网络。

深度迁移学习利用源域大量有标签数据训练得到预训练网络，预训练网络获得的权重和偏置已经很好地适应源域情况。当目标域数据与源域数据的分布相近时，就可以在源域预训练网络的基础上，将预训练网络的前层冻结，不参与反向传播；只是训练最后的几层，让最后的几层连接参数更新，即微调，就可以达到较好效果。

由此可以看出，迁移学习的主要优点：数据量需求少，源域预训练模型已经具备了大量的参数，只需要少量的目标数据来训练最后一层或者几层网络，以使模型可以很好地适应目标域的情况。这就很好地契合了在目标井上用少量测井及岩芯数据准确预测孔隙度的需求。

2.2 基于TDNN 孔隙度预测模型的建立

2.2.1 PTDNN 预训练模型构建

1）实验数据处理

由于测井工况和仪器工作状态或者其他因素的影响，测井数据中常常存在缺失值和异常值。这些异常值和缺失值会直接影响孔隙度预测模型的性能。

对于缺失值，有两种处理策略：1）整个测井属性值全部缺失或者超过50% 缺失的情形下，删除整个测井属性；2）测井属性缺失少量值，据熊中敏等[21]和陈娟等[22]的方法，采用该属性的均值填补。对于异常值，直接剔除。

为了使神经网络的泛化能力提高，可以适应不同地质层参数情况，从而准确预测不同地质层的孔隙度，将用于训练的测井数据按行随机打乱，对应深度的岩芯孔隙度作为标签。初步处理后的部分测井数据及对应孔隙度如表1 所示。

表1 初步处理后的部分A1 井测井数据及对应孔隙度Tab.1 Part of well logging data and corresponding porosity of Well A1 after preliminary processing

经过上述一系列处理后，所得数据已经可以用于初步分析。但对于深度神经网络的训练来说，还需要归一化处理，即把数据归一化为[0，1]。由于各种测井属性数据的量纲不同，从而不同属性数值差距较大，会导致神经网络在训练过程中对数值较大的属性产生严重依赖，数值较小的属性被忽略的现象。进而严重影响模型的预测性能。为此，使用式（9）对数据进行归一化处理

式中：

xs—归一化后标准数据；

x—原始数据；

xmin—某一测井属性原始值的最小值；

xmax—某一测井属性原始值的最大值。

2）网络输入测井属性的选择

测井工程数据包含众多的测井属性数据，需要根据不同的目标对其优选。对于本文所研究的孔隙度，根据文献[23-24]选择常用的一些测井属性，如声波时差（AC）、电阻率（RT）、密度（DEN）、自然伽马（GR）、光电截面积指数（PE）、井径（CAL）、补偿中子（CNL）、泊松比（POIS）和其他相关的测井属性。

由于深度神经网络是反映输入与输出之间的非线性关系，因此，必须保证输入的测井属性两两之间是非线性关系[25]。但是部分测井数据之间可能存在着高度的相关性，需要用一定指标衡量测井属性之间的相关性加以筛选。

使用皮尔逊相关系数法来计算A1 井、B1 井各测井属性之间的相关系数。皮尔逊相关系数的计算模型为

式中：

r(X,Y)－两变量间的相关系数；

Var()－变量的标准差；

cov(X,Y)－两变量间的协方差。

一般认为，|r(X,Y)| ≥0.8 两变量间的相关性很高，0.3 ≤|r(X,Y)| ＜0.8 两变量间的相关性较弱，|r(X,Y)|＜0.3 两变量间没有相关性。

计算A1 井和B1 井测井数据间相关系数如表2和表3 所示，据此，优选出A1 井的AC、RT、DEN 及GR 共4 个测井属性作为深度神经网络的输入，B1 井的AC、DEN、DTC、GR 及PE 共5 个测井属性作为深度神经网络的输入。

表2 A1 井各测井属性的相关系数Tab.2 Correlation coefficients of each logging attribute of Well A1

表3 B1 井各测井属性的相关系数Tab.3 Correlation coefficients of each logging attribute of Well B1

3）源井预训练网络的搭建

用于源井A1 井和B1 井的孔隙度预测网络训练和测试数据量的情况如表4 所示。

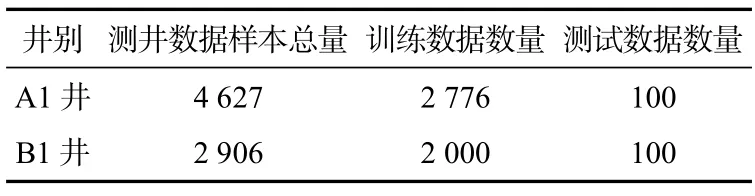
表4 各井训练数据情况Tab.4 Training data of each well

A1 井有4 个输入属性，因此，输入层设置节点为4。考虑到A1 井用于训练的数据样本数为2 776，根据张勇等[26]提出的方法，隐藏层节点数目nN等于输入层节点数目nF2 倍加1（nN=2nF+1），决定设置第一隐藏层神经元节点数目为9。经过多次实验，对比网络的预测精度发现，后续的网络结构设置效果最佳：第一、第二和第三隐藏层神经元节点分别为9、9 及4，输出层神经元节点数为1。

B1 井有5 个属性，按照A1 井同样的方法设置网络。输入层节点数为5，第一、第二和第三隐藏层设置节点为11、11 及5，输出层为1。构建的A1 井和B1 井预训练深度神经网络如图3 所示。

图3 源井孔隙度预测深度神经网络的结构Fig.3 The structure of the source well porosity prediction depth neural network

2.2.2 PTDNN 模型构建

在孔隙度预测深度神经网络初始训练模型建立好的基础上，构建目的井的孔隙度预测迁移深度神经网络。

在测井过程中，由于部分储层厚度较小或者其他原因，使得某些层组的测井数据稀少，在此情形下，就难以训练得到性能优异的深度学习模型。再者，岩芯的获得和完整地开发一口新测试井的成本都极其高昂。深度迁移学习可以充分应用同一区块相邻的其他测试井的历史测井数据，只需要少量新井的测井和岩芯数据，从而可以大大降低勘探成本并且发挥出深度学习高精度的优势。

1）两组源井与目标井井间MMD

由2.1.2 节知，迁移学习的性能和源域与目标域数据分布相似性有很大关系，在本文中也就是有大量测井数据的源井与只有少量测井数据的目标井的测井数据分布相似性。因此，需要计算A1 井与A2井和B1 井与B2 井间的最大均值差异，为了计算简便，使用更为常见的线性核作为最大均值差异的核函数。计算所得最大均值差异如表5 所示。

表5 B1 井与B2 井和A1 井与A2 井间的最大均值差异Tab.5 MMD between Wells B1 and B2 vs Wells A1 and A2

2）两目标井的PTDNN 模型

将在B1 井上训练得到的深度神经网络作为预训练模型在B2 井上微调，即以B1 井（源井）为源域，B2 井（目标井）为目标域。将B1 井上训练得到的神经网络输入层，第一和第二隐藏层参数冻结，第三隐藏层和输出层参数进行训练，使得其参数更新而适合B2 井的地质情况。

A2 井迁移网络训练策略同B2 井一致，将A1井上训练得到的神经网络输入层，第一和第二隐层冻结，第三隐层和输出层用200 个A2 井测井数据进行再训练。最终构建的用于A2 井总孔隙度预测PTDNN 如图4 所示，由于B2 井的迁移网络结构也类似，故展示出A2 井PTDNN 结构图（图4）。

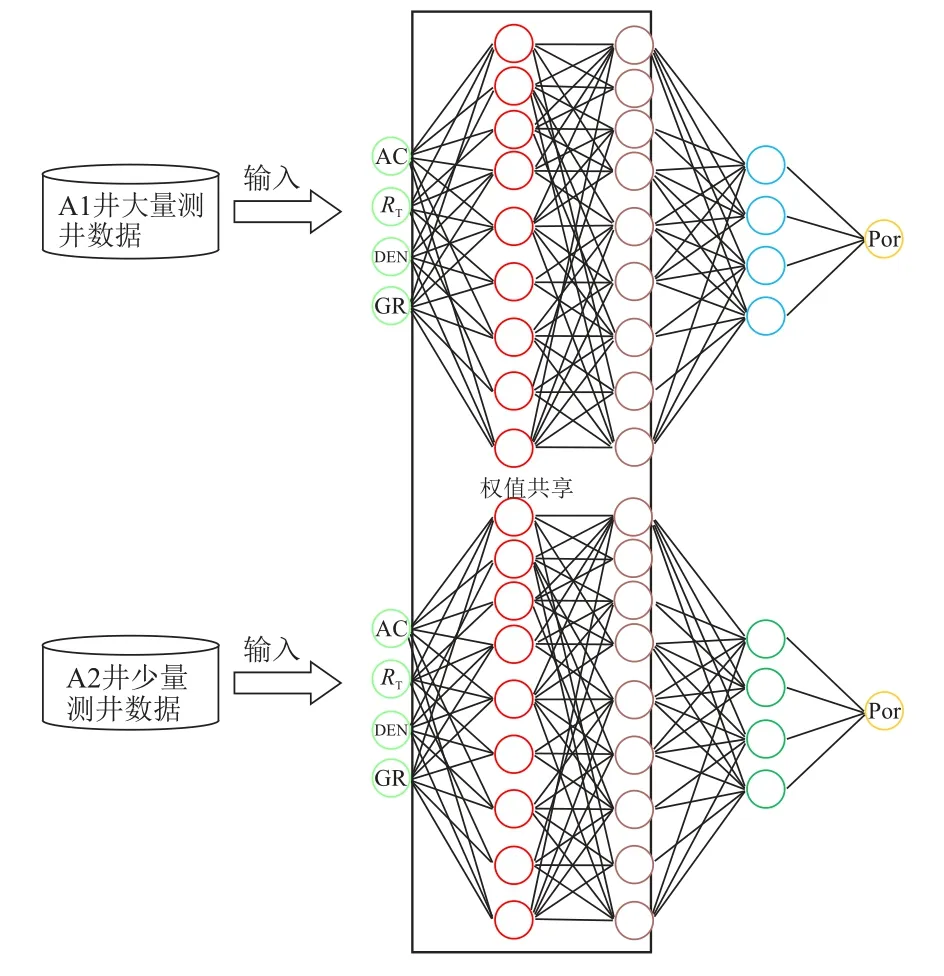
图4 A2 井PTDNN 结构图Fig.4 The structure of PTDNN of Well A2

3 PTDNN 孔隙度预测性能分析评价

对使用200 个测井数据（仅为初始训练模型数据需求量的10%）以及对应的岩芯孔隙度构建的PTDNN 性能进行评价分析。首先，分析输入数据组成结构对PTDNN 性能的影响，训练得到孔隙度预测性能最佳的PTDNN 的模型参数，分析PTDNN在两口目标井上的性能差异及其原因；其次，分析PTDNN 与DNN 和随机森林回归（Random Forest Regressor，RFR）的性能对比。

用绝对均值误差（Mean Absolute Error，MAE）、MSE 和决定系数R2衡量模型在测试数据上的孔隙度预测性能。MAE 反映模型预测整体误差的大小，R2反映模型预测孔隙度曲线趋势和岩芯分析孔隙度趋势的拟合优度。从量和趋势两方面可以更为精确地衡量模型的预测性能。其计算模型如式（11）和式（12）所示

式中：L2—绝对均值误差；

li,—岩芯孔隙度真实值和模型孔隙度预测值；

l—li组成的向量形式。

MAE 越小，R2越大，模型预测孔隙度性能越好。

3.1 输入数据对PTDNN 孔隙度预测性能的影响

为探究目标井训练数据的组成情况对于PTDNN 性能的影响，将B1 井（源井）测井数据抽样加入到B2 井（目标井）共同组成B2 井的训练集数据，保持其他参数不变。将B1 井和B2 井训练数据比设置为0：200，1：1 和1：2，即，B1 井和B2 井测井数据集数据量分别为0 和200、100 和100、60和140 共3 种情况。其MAE 如表6 所示。

表6 B2 井训练集数据组成情况对于网络性能的影响Tab.6 The impact of the data composition of the B2 training set on the network performance

通过表6 可以看出，在同样量的训练数据的情况下，训练数据的组成情况对于神经网络的性能会产生影响。迁移深度神经网络训练数据全部使用目标井数据相较于目标井和源井各1/2 的情况，MAE低0.054 8。PTDNN 使用目的井的测井和岩芯孔隙度作为训练数据更好。

对于这一现象可以理解为：在预训练网络的再训练过程中，前面的层已经冻结了，网络参数不再更新，只是后面的一两层参与训练。此时，目的井训练数据占比越大，所更新的参数，更适合新情况下的属性与标签间的映射关系。

3.2 PTDNN 在目标井上的孔隙度预测性能

通过3.1 节可知，全部使用目标井可以使得PTDNN 获得最佳预测性能。由此，选用200 个目标井的测井及岩芯孔隙度数据，多次调整PTDNN 的超参数训练过程中的损失变化情况，得到在目标井B2 井和A2 井上的最佳孔隙度预测性能如图5 和图6所示。

图5 PTDNN 在目的井训练过程中损失曲线Fig.5 PTDNN′s loss cure on target wells

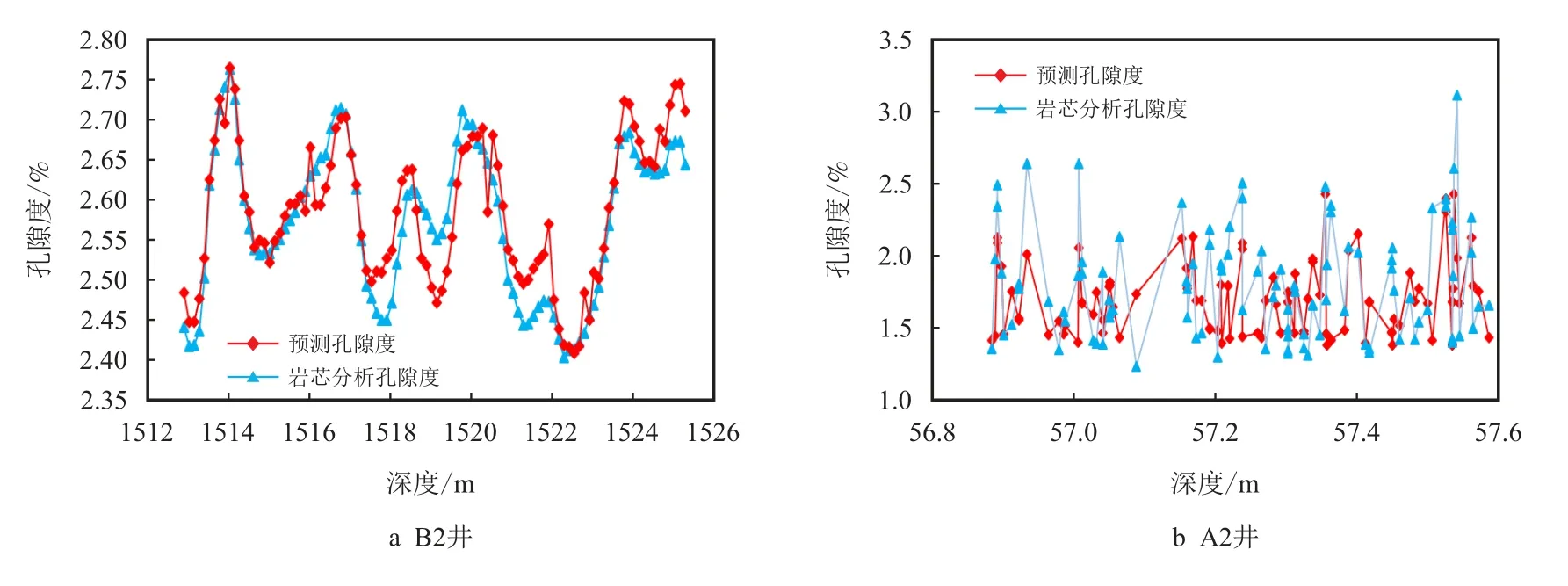
图6 PTDNN 在目的井上的孔隙度预测效果图Fig.6 PTDNN′s porosity prediction performance on target wells

计算得到PTDNN 在两井上的量化指标MAE、MSE 和R2如表7 所示。

表7 PTDNN 在目标井上的孔隙度预测性能指标Tab.7 PTDNN′s porosity prediction performance index on target wells

图6 和表7 展示了PTDNN 在两目标井的孔隙度预测性能。在B2 井上，其MAE 仅为0.032 9，R2达到了0.814 6。PTDNN 预测值与岩芯分析孔隙度误差很小，并且预测曲线与孔隙度实际值曲线相关性很高。在B2 井上训练得到的PTDNN 可以有效地预测储层孔隙度，可以从图6a 中得到直观的体现。

同时，表7 和图6 也表明，PTDNN 在B2 井和A2 井上预测性能存在较大差异，在A2 井上的MAE高于B2 井0.265 0，R2比B2 井低0.803 2，其性能远低于B2 井。从图6b 也可以看出，在A2 井上PTDNN 预测值都不能跟踪岩芯孔隙度。

造成这一现象的原因是：B1 井与B2 井和A1井与A2 井间的MMD 存在较大的差异，表5 的计算结果显示：A1 井与A2 井间MMD 是B1 井与B2井的4 倍，也就是说，B1 与B2 井间非均质性差异远小于A1 井与A2 井。

3.3 PTDNN 与DNN 和RFR 孔隙度预测性能对比

为比较PTDNN 与其他模型的孔隙度预测性能，用同等数据量训练了DNN 和RFR 模型作为对比。

随机森林回归是一种非深度学习的机器学习算法，由多个不同的回归决策树组成。多个回归决策树作为基回归器，增强了模型的鲁棒性及准确率。

通过多次训练两模型的参数，得到DNN 和RFR 最佳孔隙度预测性能如图7 所示。

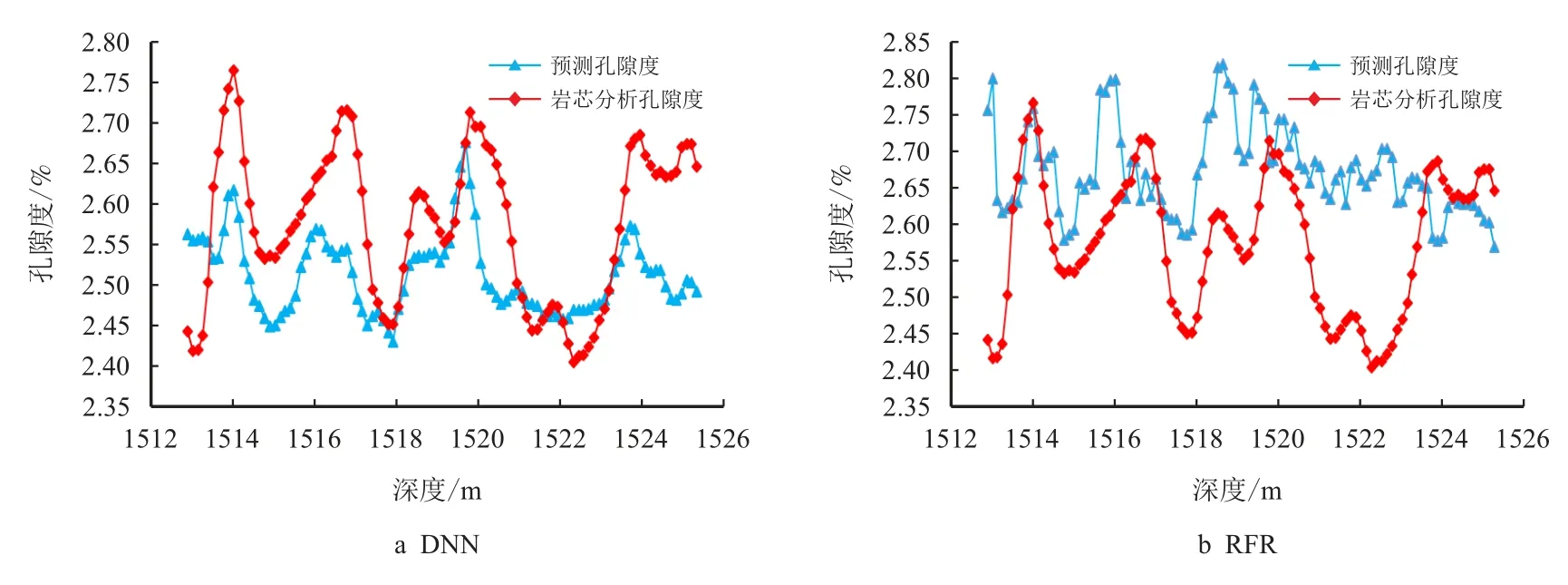
图7 DNN 和RFR 在B2 井上的孔隙度预测性能Fig.7 DNN and RFR′s porosity prediction performance on Well B2

计算得到不同模型在B2 井上的量化指标MSE、MAE 和R2如表8 所示。

表8 不同模型在B2 井上的孔隙度预测性能指标Tab.8 Porosity prediction performance indexes of different models on Well B2 MAE,MSE,R2

图7 及表8 表明，在预测误差方面，DNN 和RFR 都大于PTDNN，RFR 的孔隙度预测误差甚至接近PTDNN 的4 倍；在预测曲线和岩芯孔隙度曲线相关性方面，DNN 的R2为0.516 7，DNN 预测值还可以跟踪岩芯孔隙度变化的趋势。但是，RFR 的R2为-1.103 0，基本上不存在相关性了，已经不能跟踪岩芯孔隙度变化的趋势。

以上两种模型与PTDNN 的对比表明，深度学习网络比非深度的机器学习方法，其预测孔隙度的性能更好；PTDNN 由于有了预训练的过程，使用少量新井的测井及岩芯数据训练PTDNN 就可以比其他方法更准确地预测储层的孔隙度。B2 井的PTDNN 相较于预训练模型，数据需求量降低了90%。

因此，只要找到与待确定参数的目标井测井数据分布相似的有大量测井数据的其他井，就可以应用深度迁移学习的方法来很好地预测目标井的其他关键储层参数，例如，渗透率和含气量等。

4 结论

1）针对页岩孔隙度难以用常规油气储层的规律进行表征预测的问题，创新性地提出迁移深度神经网络模型用于孔隙度预测，用少量数据实现页岩孔隙度的准确预测。借助于神经网络强大的非线性拟合能力，有效地避免了复杂的物理数学建模过程，从而极大减小孔隙度预测误差。

2）实验证明，提出的MMD 衡量两井地质差异性的有效性。并且，迁移深度神经网络PTDNN 的性能与源井和目标井的测井数据分布相似性密切相关，只要相似性在一定的阈值之内，就能实现有效的迁移。通过实验的对比，做到了井间的有效迁移学习，达到了充分利用历史测井数据来预测新井的目的；在同样大小测井数据量作为训练数据的情况下，PTDNN 的孔隙度预测性能优于DNN 和RFR，都充分表明了提出的迁移学习方法的优势。降低了新井对于大量测井数据，尤其是成本高昂的岩芯数据依赖，可以极大地降低企业的勘探成本。

3）当下，深层页岩气的开发也已成为石油天然气工业的紧要任务，但是其地质工程参数与浅层页岩存在着较大差异，迁移学习方法充分利用相似的历史测井数据这一特性，同样也可以为深层页岩气的重要地质参数的预测提供一种重要手段。