表征视角下的数形结合思想方法引导探究
2024-01-12李成蔡庆有
李成 蔡庆有



【摘 要】 问题表征是解决问题的一种有力工具,而数学表征能力是学生数学核心能力之一的体现.中学数学的主要研究对象就是以数量关系与空间形式所表征出现的问题,“数”与“形”的各自表征体现出严谨的逻辑思维和直觉的感知思维,研究“数”与“形”的结合方法在一定程度上也拓宽了这两种思维的培养路径.
【关键词】 高中数学;表征;数形结合
1 概念综述
1.1 数学表征
在心理学中表征一词概念为“信息在大脑中的呈现就称为表征”.徐斌艳对于数学表征站在变换能力的角度定义为:“用某种形式,例如书面符号、图形(表)、情景、操作性模型、文字(包括口头文字)等,表达要学习或处理的数学概念或关系,以便最终解决问题”[1].从数学表现形式上将数学概念或问题划分为符号(文字)表征和图示表征.例如集合的表示法中的描述法就是用符号语言来下定义集合概念的,而图示法(维恩图法)就是用几何图形重叠的区域表示集合的一种方法,两种方法都是对集合概念的描述方法.符号表征具有历时性,是对数学概念的信息的抽象化数字表征.图示表征具有共时性,是对数学知识的内涵的直观化的形象表征.问题解决表征呈现形式不同,采取的解决路径也是大相径庭.
1.2 数形结合
数与形是数学学习的两大主题.从毕达哥拉斯的“万物皆数”到笛卡尔解析几何的建立都是“数形结合”在历史长河中的痕迹[2].将一个代数问题转化为一种特定形式的几何问题,便可直观化地分析出问题中要素关系以及其解法;将一个几何问题代数化后,便可抽象化精准化地测量出几何要素的位置关系[3].数形结合的实质就是通过对数与形在符号形式与空间形式上的对应转换,使得数量关系与空间形式在某种机制下相得益彰、水乳交融[4].
2 表征视角下的数形结合思想方法引导探究
数形结合的思想方法在高考中的考查属于重点和难点,考查学生的代数运算能力和图形空间想象能力.作为一种解题技巧,无非就是两种情况(形化为数和数化为形),但是从高中数学知识的表征形态来看,以知识层面对数形结合思想的运用分类为三种表征对象:①方程、不等式、代数式最值;②平面几何和立体几何;③代数和几何的桥梁者(函数和向量).这些都是独立的知识体系,数形结合的考查要点就是对这几种知识体系的转换.根据不同知识点的不同表征形态划分转化,使得数形结合解题思路清晰有章可循.已有的成固定思维的数形结合本文不再探究,例如方程的根与函数图象零点问题、用建系法解决平面或立体几何中位置关系等问题.高级段的数形结合应是跨度大但有深层联系的不同知识板块的数形结合,这也是近年来高考的难点和学生思维的障碍点.
2.1 平面几何表征解决方程问题
.
思路 方程组中后两式与余弦定理可联系,余弦定理与三角形有密切联系,此题的方程表征就转换到三角形几何表征了.
评价 本题的突破点在于方程能否转化为余弦定理公式,其次根据余弦定理与几何图形(三角形)的联系性,运用等积法解决.
2.2 立体几何表征解决不等式问题
观察变化后不等式,发现左边类似于勾股定理,那么我们就能进一步联想为在长方体中各边构造关系来解决问题.
评价 本题的突破点在于利用勾股定理把问题引入到几何表征中,值得强调的是,勾股定理多在平面几何中出现,能联想到立体几何空间中去构造长方体是此题突破点.
2.3 函数表征解决代数式最值问题
评价 采用整体视角去发现代数式中两点间距离公式是本题的解答关键所在,之后的构建函数利用图象来找最值就迎刃而解了.
2.4 等式表征解决平面几何“长度”问题
思路 从题的表征形式上看,这是一道几何求线段长的問题,那么其中的各条几何线段必存在某种数量的联系,这就会让学生联想到用以三角形为工具展开的“勾股定理”或“三角函数”来解决此问题了.
评价 此题的转化角度在于要明察到线段长度背后的代数关系,这里的表征突破点在于几何图形里的直角三角形勾股定理的运用,因为从代数的角度看,勾股定理就是平面几何中线段长度的关系桥梁,当然了,还有三角函数.
2.5 向量表征解决平面几何“角度”问题
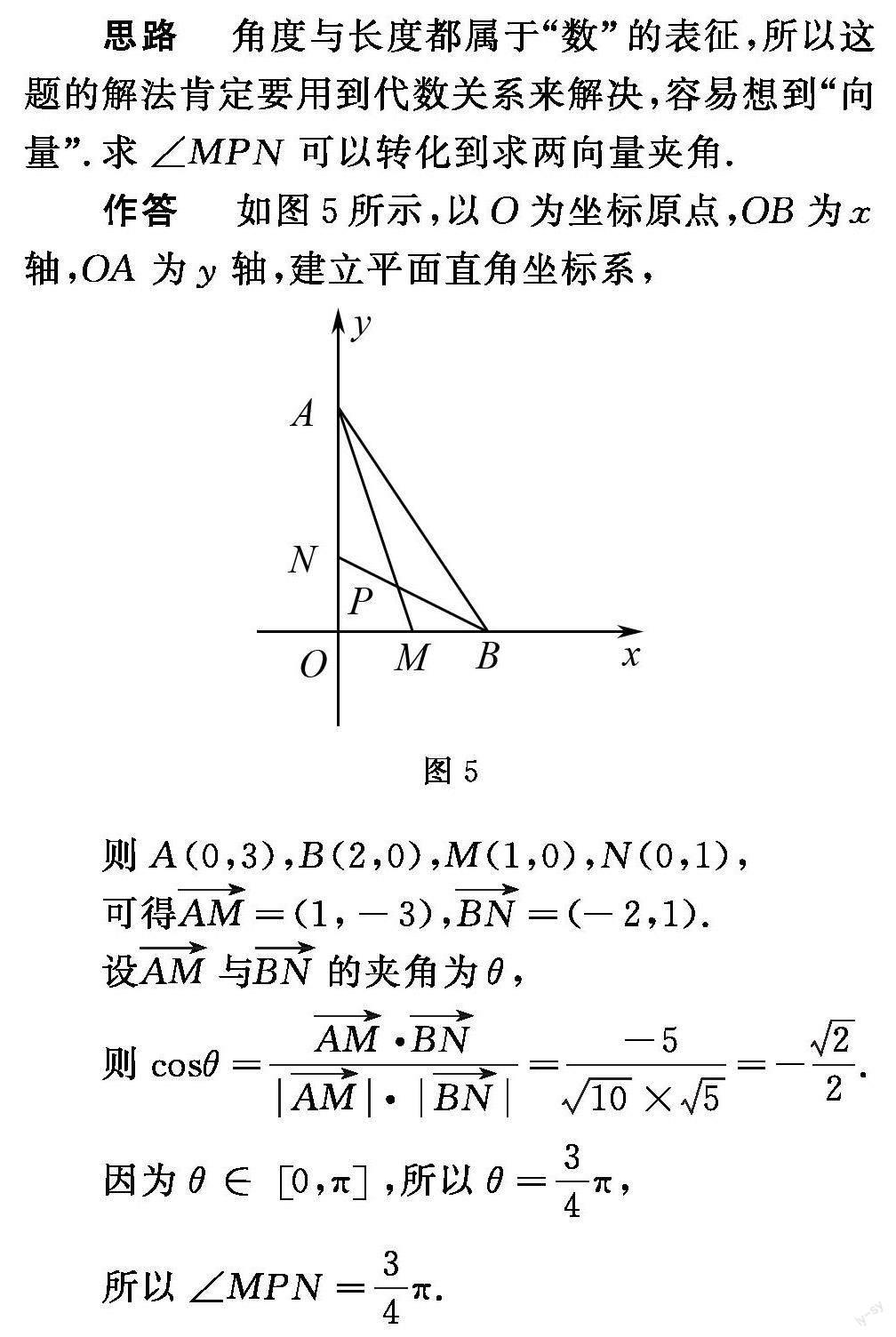
思路 角度与长度都属于“数”的表征,所以这题的解法肯定要用到代数关系来解决,我们就容易想到“向量”.求∠MPN可以转化到求两向量夹角.
评价 几何题中求解角度的问题从实质性上讲就是代数问题,但是需要在无序的图形中搭建适宜的坐标系以及找准对应的向量关系,这样后续的代数运算才能事半功倍.
3 结语
数形结合思想方法作为高中数学的必备解题思想策略之一,也渗透了转化、类比、分类等重要数学思想,值得强调的是数形结合的运用要具体情况具体分析,切记不可生搬硬套.学生要深入研究高中知识板块,明了哪些板块之间可以运用“数形结合”思想搭建起沟通桥梁,以便解题思路的清晰和过程的简便.
参考文献:
[1]徐斌艳.数学学科核心能力研究[J].全球教育展望,2013,42(06):67-74+95.
[2]魏芳.数形结合,让数学学习更有意义[J].教学与管理,2012(32):33-34.
[3]李巧文. 数形结合的心理机制[D].西安:陕西师范大学,2008.
[4]刘星红.例谈“数形结合”应用的四个误区[J].数学通报,2007(11):48-49.
