探究如何利用谐振电路准确测量电容和电感

鲁 润

(永宁县第二中学 宁夏 银川 750100)

在电感、电容和电阻三者串联或并联组成的简单电学振动系统中,当正弦波信号源的输出达到某一频率时,RLC电路的电流达到最大值,即产生谐振现象．发生谐振现象时,电路中的电流、电压、阻抗、容抗、感抗等相关参数均处于某种特殊状态,因而在实际中有着重要的应用,如在放大器、振荡器、滤波器电路中常用作选频电路．那么能不能利用谐振电路的这一特性测量电容和电感呢?笔者利用RLC电路谐振时电路参数之间关系,采用控制变量法,推导出测量电容和电感的理论基础;通过设计实验,多次测量探究,并对相关数据深入分析,发现利用RLC串联谐振电路测量电容和电感是切实可行的,但要想准确测量电容或电感是有条件的;最后还探究了电阻的改变对实验结果影响．

1 实验原理

1.1 利用RLC串联谐振电路测量电容和电感

在RLC串联电路中,若接入一个电压幅度一定,频率f连续可调的正弦交流信号源(图1),则电路参数都将随着信号源频率的变化而变化．

图1 RLC串联谐振电路

电路总阻抗

图2 RLC串联谐振电路I随ω的变化曲线

谐振时,通常用品质因数Q来反映谐振电路的固有性质,有

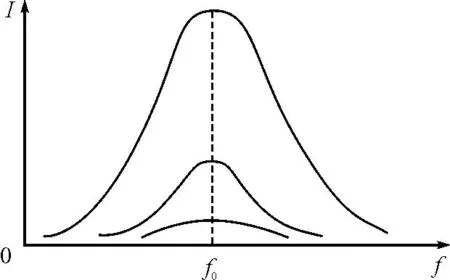
图3 I-f关系图

在谐振时,UR=Ui,UL=UC=QUi,所以电感和电容上的电压达到信号源电压的Q倍,故串联谐振电路又称为电压谐振电路．

在RLC串联电路中,当调节电源频率,使其满足XC=XL时,则电路中的电流和电源电压同相位,电路的阻抗Z0为最小,Z0为谐振阻抗,且Z0=R,而电路中的电流为最大,也就是R两端的电压最大,所以调节信号发生器的输出频率与毫伏电压表上的读数变化趋势如图4所示．

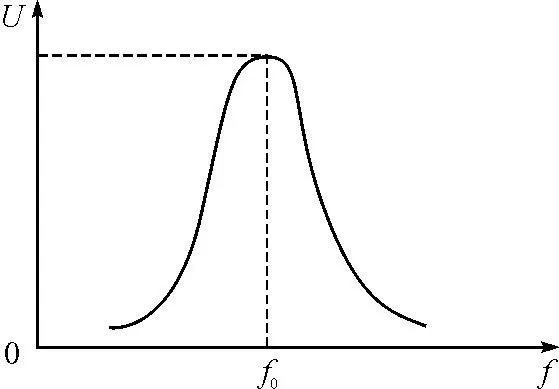
图4 电压表读数变化趋势图

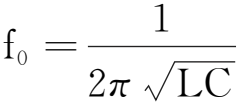
根据谐振特点,当信号源端输出电压相同的情况下,观察电阻R两端电压U是否达最大值来判断电路何时发生谐振[1]．只要记下电路在最大电压UR时对应的输出频率,即为谐振频率f0,就可以计算出电感L,因为此时谐振频率为

则线圈电感

所以在RLC串联电路中,如果已知电容,就可以求出电感．

反之,已知电感,就可以求出电容．

1.2 利用RLC并联谐振电路测量电容和电感

并联谐振是指在电阻、电容、电感并联电路中,出现电路端电压和总电流同相位的现象．

我们知道,电路在并联谐振时的谐振频率为

一般情况下,线圈的电阻远小于线圈感抗,即RL=XL,若忽略线圈电阻RL,则有

确定谐振频率后,由公式即可计算出线圈电感L的大小,反之,若已知电感,就可以求出电容．在并联谐振电路中,回路的总电流I为最小,谐振回路的总阻抗为最大,所以U的波形幅值为最大．因此,并联谐振也叫电流谐振．

2 实验仪器与装置

实验装置如图5所示．YB2172型交流毫伏表, DH4503型RLC电路实验仪．

图5 实验装置图

3 实验方法

检查实验仪器,按照图6所示实验线路图连接线路．L和C之值为实验仪器的标称值,根据电感和电容的选取,选择一个适当的R值,本实验中R=30 Ω．当S与“2”接通,调节US的电压输出幅度,保证各种频率测量时的有效输出电压值都是1.0 V．

图6 实验线路图

3.1 利用谐振电路测量电感

(1)当开关S拨向“1”时,交流毫伏表测量的是电阻R两端电压UR．假定已知电容C,保持信号源的输出幅度恒定为1.0 V．

(2)改变信号源频率,用交流毫伏表测出相应频率下UR的大小．

(3)找出电阻R两端电压UR最大值,对应的频率f0即为谐振频率[2]．

注意：因为信号源不是恒压源,它有固定的内阻,而外电路是随频率变化而变化的阻抗,因而信号源的输出幅度也必然随频率改变而变化．这就给测量UR的最大值带来了麻烦,必须反复多次调节输出电压US,保证各种频率测量时的有效输出电压值都是1.0 V,以提高实验准确性．

(4)改变电容C,重复以上三步,进行多次实验．

(5)将实验数据代入,计算可得电路中的电感．

3.2 利用谐振电路测量电容

(1)当开关S拨向“1”时,交流毫伏表测量的是电阻R两端电压UR．假定已知电感L,改变信号发生器的频率,观察记录各次频率变化和交流毫伏表变化情况(幅频特性),确定UR的最大值以及此时的谐振频率f0．

(2)按照以上3.1(1)到3.1(3)实验操作方法,确定电容变化时,对应的谐振频率f0．

(3)将实验数据代入,计算可得电路中的电容．

3.3 电阻对电路的影响

(1)调节实验仪器使U=1.0 V,C=0.04 μF,L=110 mH,改变信号发生器的输出频率f,分别记录当电阻R=30 Ω时和R=300 Ω时的实验数据．

(2)按照上述步骤,可再次调节实验仪器使U=1.0 V,R=30 Ω,C=0.5 μF,L=10 mH,改变信号发生器的输出频率f,分别记录当电阻R=30 Ω时和R=5 kΩ时的实验数据．

(3)多次测量,对实验数据进行分析处理,得出结论．

4 实验数据及处理

4.1 利用串联谐振电路测量电感可行性研究

实验中U=1.0 V,R=30 Ω,改变信号发生器的频率f,其他实验数据见表1～4.

表1 C=0.5 μF时实验数据

对表1数据进行处理:标准电感L=10 mH,将数据代入,则有

实验相对误差

表2 C=0.6 μF时实验数据

同理对表2数据处理,标准电感L=10 mH,则有

L′=1.018 4×10-2H

实验相对误差

ε=1.84%

表3 C=0.05 μF时实验数据

同理对表3数据处理,标准电感L=10 mH,则有

L′=1.010 1×10-2H

实验相对误差

ε=1.01%

表4 C=0.06 μF时实验数据

同理对表4数据处理,标准电感L=10 mH,则有

L′=1.004 8×10-2H

实验相对误差ε=0.48%

由表1到表4数据分析、处理,可以看出:利用RLC串联谐振电路测量电感是切实可行且误差较小的．

4.2 利用谐振电路测量电容可行性研究

实验中U=1.0 V,R=30 Ω,其他实验数据见表5～8．

表5 L=50 mH时实验数据

对表5数据处理:

标准电容C=0.5 μF,将数据代入,则有

5.015 8×10-7F

实验相对误差

表6 L=60 mH时实验数据

同理对表6数据处理,标准电容C=0.5 μF,则有

C′=5.098 1×10-7F

实验相对误差

ε=1.96%

同理对表7数据处理,标准电容C=0.5 μF,则有

C′=4.991 1×10-7F

实验相对误差

ε=0.18%

表8 L=3 mH时实验数据

同理对表8数据处理,标准电容C=0.5 μF,则有

C′=5.000 9×10-7F

实验相对误差ε=0.018%

由表5到表8数据分析,可以看出:利用RLC串联谐振电路测量电容是可行且误差较小的．

4.3 利用RLC串联谐振电路准确测量电感的研究

实验时U=1.0 V,R=30 Ω,标准电感为110 mH,其他实验数据见表9.

表9 改变电容实验数据及处理

续表9

说明：σL为实验相对误差．

通过表9实验数据分析,可以看出:利用RLC串联谐振电路准确测量电容,是有条件的．当电感一定,电容比较小时,测得的电感相对误差比较大．经过多次实验,得出若电容C大于3.9×10-9F时,利用DH4503型RLC电路实验仪能够较准确地测量电感,可以将相对误差控制在5%以内．

综上所述,在电容已知的情况下,如果电容较大,可以利用RLC串联谐振电路较准确测量电感．

4.4 利用RLC串联谐振电路准确测量电容的研究

实验中U=1.0 V,R=30 Ω,标准电容为1.1 μF,其他实验数据见表10．

表10 改变电感实验数据及处理

说明：在使用的DH4503型RLC电路实验仪中,电感的变化范围是有限的．只能在1～110 mH之间变化,所以本实验所得出的结论可能具有局限性．σC为实验相对误差．

通过表10实验数据分析,可以得出:在实验的误差范围内,无论电感值是大是小,都可以利用RLC串联谐振电路较准确地测量出电路中的电容．

综上,在电感已知的情况下,可以利用该仪器较准确地测量电容,而不受电感值大小的影响．

4.5 探究电路中电阻对实验的影响

(1)实验中U=1.0 V,C=0.04 μF,L=110 mH,改变电阻,实验数据见表11和表12．

表11 R=30 Ω时实验数据

表12 R=300 Ω时实验数据

对表11和表12数据进行对比分析,可以看出:改变电阻,在实验误差范围内,对实验结果基本没有影响．

(2)实验中U=1.0 V,C=0.5 μF,L=10 mH,改变电阻,实验数据见表13和表14．

表13 R=30 Ω时实验数据

表14 R=5 kΩ时实验数据

从表13和表14可以看出,当电阻较大(实验中R=5 kΩ)时,调节信号发生器的频率f,发现R两端的电压只在0.980～1.00 V之间变化,变化幅度非常小,难以准确读数,这给确定RLC串联谐振电路的谐振频率f0带来很大困难,所以在这种情况下,利用谐振电路是无法准确测量电感和电容的．

这种现象的本质原因分析:

(1)由于实验采用通过改变输入信号的频率,观察电阻R上的最大输出电压,来获取谐振频率f0的方法,如果电阻R比较大,就会造成谐振品质因数Q值太低,谐振强度不够,谐振频率附近电阻R两端电压变化不灵敏,所以电压的变化范围必定很小．

(2)在串联谐振时由于电感与电容两端的电压降大小相等方向相反,在电路中他们的作用是彼此抵消的,所以外加电压相当于完全被电阻R所消耗,即U=UR=IR,显然此时电路中的电流值就只取决于电阻R,而与电感L和电容C无关,也就是说无法进行测量．

综上所述,虽然理论上电阻的改变并不影响结果,但是为了提高测量的准确度,在实际测量过程中,建议应选取阻值较小的电阻进行实验．

5 讨论

通过多次实验探究,发现利用RLC串联谐振电路测量电容和电感是切实可行的,但要想准确测量电容或电感是有条件的．

(1)在电容已知的情况下,当电感一定,电容比较小时,测得的电感相对误差比较大．当电容C大于3.9×10-9F时,利用DH4503型RLC电路实验仪能够较准确地测量电感,可以将相对误差控制在5%以内.

(2)在电感已知的情况下(电感量只能在1～110 mH之间变化),可以利用RLC串联谐振电路较准确地测量电容,但应注意控制电阻R为较小值．

注意在本实验中笔者使用的是毫伏电压表判断电路何时发生谐振,所以必须保证在端电压输出相同的前提下比较测量值UR,至于我们能否在确定谐振频率时引入示波器?示波器是不是测量更为直观、准确?可以作为另一个设计性实验进行研究．实验过程中还应注意不能长时间持续实验,不然会造成谐振电路的LC总内阻发生变化、谐振频率不稳定、谐振品质因数低、电路损耗较大、一些特性不稳定等等[3]．