丢勒的几何学

周施廷

摘要丢勒将几何理论具象化为图像知识，以此改造德意志传统艺术，使其焕发出一种以精确性为特征的新艺术风格。作为德意志的科学和印刷中心，丢勒的家乡纽伦堡汇集了一批优秀的学者和工匠。在数学家雷格蒙塔努斯的影响下，丢勒对几何学产生兴趣并认识到结构之于图像的关键作用。在前往威尼斯学习之后，丢勒对几何学进行了文字、装置和图像三个层面的处理，将数学变为一种可视化知识，从而解决了几何理论难以理解和应用的实践问题。丢勒的创造性改革不仅让数学内化为德意志艺术设计的知识体系，同时也激发出德意志工匠的创作热情，他们纷纷执笔著述，完成从工匠到作者的身份转变，而丢勒本人的著作也在16世纪中期被广泛译介至法国、意大利和尼德兰等地。

数学可以让艺术作品获得精妙细腻的美感，从而克服德意志传统作品的刻板问题。对丢勒而言，这种以精微、精湛为主要特点的新艺术风格建立在数学的基础之上。他通过对几何原理进行具象化处理，将形象思维和抽象思维相结合，以想象力考察数学和艺术之间的微妙关系。在欧洲大陆上，数学和艺术的融合始于15世纪的意大利。亚平宁半岛上蓬勃的贸易活动使得人们对艺术品的需求大增，这既提高了画家的社会地位，也带来行会-学徒制的衰退，画家与人文主义者实现了特殊的联合。据阿诺德·豪泽尔（Arnold Hauser） 的分析，这种现象与艺术家渴望得到人文主义者的友谊有关：他们希望向具有人文主义思想的上层阶级证明自己通过绘画赢得经济地位的努力是正确的，以此摆脱“工匠”的身份印记；此外，画家也想要得到人文主义者在科学方面的建议，因为“在创作畅销的神话和历史题材作品时需要他们的帮助”①。

在几何原理内化为艺术结构之后，意大利文艺复兴时期的作品迸发出前所未有的璀璨光芒，这种情况也引发了丢勒对德意志艺术发展的深切忧虑，因为相比同时代富有创新精神的意大利人，德意志工匠在行会的束缚下长期从事机械性劳动。丢勒从第二次威尼斯之旅返回家乡纽伦堡后，便开始思考如何融合“自由七艺”（artes liberales）和“手工七艺”（artes mechanicae），并在1525年撰写出著作《圆规直尺测量法》②，成功将几何原理应用于艺术创作，为近代早期德意志绘画方法的变革奠定了重要的科学基础。近年来，欧美学界开始关注丢勒作品中的数学元素，但主要以整理图像信息为主，比如埃伯哈德·施罗德（Eberhard Schr?der） 的《丢勒：艺术和几何学》③一书梳理了丢勒运用几何原理绘制的图像；斯蒂芬·吕克金（Stephen Luecking） 和亚历山大·马尔（Alexander Marr） 聚焦于丢勒运用几何原理绘制的天体图的具体内容④。

本文认为，丢勒以视觉语言为桥梁搭建起科学理论与工艺实践交融的平台，从而改变了传统艺术的创作理路：一方面，细微精湛的新艺术风格的诞生昭示着德意志艺术与科学融合的开始；另一方面，人们完成了从工匠到作者的身份转变，拉开了艺术写作的帷幕。丢勒在其著作中展示了运用几何原理绘制图像的测量方法，工匠们在其影响下出版了简单实用的“艺术小手册”（Kunstbüchlein） ⑤，使数学与艺术的融合变得更加多元和广泛。丢勒的方法论和美学观以印刷品为载体，从德意志传播到法国、意大利和尼德兰等地，不仅改变了各地工匠对知识的看法，也对工艺品的艺术性和科学性提出了更高要求。

一、纽伦堡的工匠传统与科学研究

16世纪的科学革命为新测量体系的诞生奠定了基础，科学和传统的碰撞暴露出固有思维的缺点，同时也能推进新体系的建立。出身于纽伦堡工匠家庭的丢勒深知德意志传统工艺技术的优势，但也了解德意志艺术作品缺乏视觉表现力的劣势。如何将理论法则和实践技艺相结合，从科学的角度扭转德意志艺术的落后局面，这成为丢勒早年思考的主要问题。相较于德意志人固守陈规的僵化状态，意大利人文主义者在14世纪早期便注意到几何学与透视法之间的关系。但丁在《飨宴》中说过：“几何学是最洁白的，因为它没有错误的污点，它本身也是最确定的，其侍女被称为透视。”⑥乔托和洛伦泽蒂等文艺复兴早期画家已经能够在画作中巧妙营造出透视效果，但对美学理论和艺术技艺的讨论要到15世纪才有了突破性进展，其中最为关键的人物是阿尔伯蒂，他把《论绘画》第一卷视为数学作品，并在献词中表示“第一卷纯粹是数学著作，展示了这门高贵而美丽的艺术如何源于大自然本身”⑦。阿尔伯蒂借助几何学和修辞学充实了绘画艺术的理性内涵，从而将理论和实践更加紧密地结合在一起，同时也证明了数学方法在解决艺术问题时的特殊价值。

阿尔伯蒂的数学立场与当时画家的社会身份困境密切相关，绘画直到15世纪早期都被认为是机械性的活动，无法得到人们的普遍认可。为了提高画家的地位，人文主义者开始在古典著作中寻找古代作家关于绘画的观点，譬如阿尔伯蒂提及的昆体良对光影的讨论。瓦拉也在《拉丁语的优雅》中表示过对绘画的支持：“与七艺关系最为密切的艺术是绘画、雕刻和建筑，在过去很长一段时间里它们严重衰退，几乎与知识一起消失不见了。在这个时代，它们被唤醒并重新焕发生机。”⑧然而，绘画和雕塑仍然被排除在七艺之外。到了15世纪晚期，绘画在理论著作中已经普遍被视为一项依赖于数学及其他知识的活动，并由此获得了更为稳定的基础，因为数学隶属于七艺的范畴⑨。正如达·芬奇所言：“实践必须建立在合理的理论基础之上，而透视法则是指南和通道。沒有这些，就不可能做好任何绘画工作。”⑩

在意大利画家走上理性自由的创作道路的时候，德意志的工艺发展却始终受囿于帝国的政治状况。由于国内长期处于分裂状态，德意志的手工业作坊大多建立在帝国城市。德意志的手工业组织在1100年左右开始在文献中出现，行会则形成于13世纪中期。为了提高城市的竞争力，创造更有利的出口条件，纽伦堡在14世纪率先打破行会模式，禁止成立行会。在1348至1349年间，当地曾经爆发过一场工匠起义，德意志国王查理四世（Karl IV.） 在1349年6月13日颁令禁止纽伦堡“师傅”（Meister） 组织行会，市政府延续了这项规定，贸易的管理权也从此转移到市政府手中，由市政委员会统一管理工匠。这一改革无疑有助于提升作品的质量，而纽伦堡工匠向来以技艺精湛和人数众多闻名欧洲。在15至16世纪，纽伦堡市民的数量从3万增长至4万，其中工匠群体的人数几乎占到一半。蓬勃的手工业市场吸引了来自欧洲各地的工匠和商人，仅意大利商家就多达18家。工匠按其性质又分为“宣誓工艺”（geschworene Handwerk） 和“自由艺术”（freie Künste） 两类，这种分类主要是出于经济利益考虑。“宣誓工艺”包括纽伦堡最具经济价值的八种手工业，其贸易管理权掌握在市政府的五位委员手中，他们在从业者中挑选出八位师傅作为代表，让他们负责控制产品的质量及价格、工匠的工资、贸易合约等细则；“自由艺术”则不在其列，原因是它们产生的经济效益较低，从业者可以直接向市政府汇报，在教育、训练和工作方面也拥有更高的自由度，画工（Maler） 和雕版工（Bildhauer） 即属于此类。据约翰·诺伊德费尔（JohannNeud?rffer） 在《工匠传》中的记载，纽伦堡共有37种工匠，分工非常细致，其中绘制图像的工匠可分为画工、插画工（Illuminist） 和彩绘玻璃画工（Glasmaler）；在人数方面，诺伊德费尔列出的画工有7位、插画工有4位、彩绘玻璃画工有3位、雕版工有4位，而丢勒在画工中排在第四位。

纽伦堡工匠的作品广销外地，其客户群中还包括皇帝、国王、选帝侯和贵族，诺伊德费尔特别注明丢勒是为神圣罗马帝国皇帝马克西米利安一世（Maximilian I） 服务的画家。沃尔夫冈·施密德（Wolfgang Schmid） 提到丢勒时期的纽伦堡有一个显著特点，即来自欧洲各地的皇帝、国王和诸侯在游览城市时会参观工匠的作坊，亲自委托他们创作各种类型的作品。自由蓬勃的商业气氛使纽伦堡能吸引各地的优秀学者和工匠，他们在本地寻找富裕的赞助人，凭借出色的知识和技术获得市政委员会的认可，以取得“市民身份”（Bürgerrecht），而市民身份在纽伦堡是购买房屋和建立作坊的必备条件。然而，工匠获取知识的渠道相当有限，他们主要通过家庭教育来学习技术，制作时依据的是经验而不是理论。工匠通常子承父业，大部分出身于手工业家庭，少数人在接受学徒制教育的同时进入正规的拉丁文法学校读书。对15、16世纪的工匠而言，他们的知识水平与其未来发展密切相关。在意大利文艺复兴的成果传播到德意志之后，理论知识和古典语言都对工匠的文化程度提出了更高要求，加上德意志在15世纪下半叶迎来了社会和经济层面的剧烈变化，城市化进程不断加速，使得手工业扩张和人员流动都进入了一个全新的局面，著名学者雷格蒙塔努斯（Regiomontanus） 便在纽伦堡引发了一场科学革命。雷格蒙塔努斯是享誉欧洲的数学家和天文学家，曾为匈牙利国王马加什一世（Matthias Corvinus） 服务。马加什一世在布达（Buda） 建有一所藏书极为丰富的王家图书馆，收集了来自雅典和君士坦丁堡的科学文献，据说书籍的数量多达五万册。雷格蒙塔努斯还在1454年跟随贝萨里翁（Bessarion） 学习过希腊语，所以他能够阅读古希腊科学文献。身为宫廷的天文学家，他需要为国王制造天文仪器，从其留下的手稿可知他制造过的观测仪器有星盘、日晷和天体仪。匈牙利与波西米亚爆发战争后，雷格蒙塔努斯携带大量天文学和数学手稿，于1471年前往纽伦堡发展自己的科学事业。

在随后的四年间，雷格蒙塔努斯为纽伦堡的科学研究打下了坚实的基础。欧文·金格里奇（Owen Gingerich） 指出：“雷格蒙塔努斯在印刷术刚兴起时，便敏锐地察觉到印刷书籍在科学革命中的潜在角色，他酝酿了一个包括制造仪器、观测、翻译和写作在内的多面计划。”雷格蒙塔努斯在纽伦堡建立了一个专门出版科学著作的印刷作坊，这也是世界上第一个科学印刷作坊。他在1471年7月4日写给朋友的信件里表示，纽伦堡为他提供了与其他学者进行思想交流的机会，他打算在自己的印刷作坊里出版所有数学著作，这样才能杜绝因抄写不当造成的文本错误。此时纽伦堡的商行以生产和经营金属制品及精密仪器为主，雷格蒙塔努斯所拥有的技术知识正好切合城市的经济需要，譬如天文学知识可以用来指导日晷和天体仪等航海仪器的生产。同时，他也带去了阿尔伯蒂《论绘画》的抄本，阿尔伯蒂的直线透视法以及书中对阿基米德和欧几里得的介绍一并传播到了纽伦堡，丢勒即通过雷格蒙塔努斯接触到了这部作品。

印刷革命不仅改变了人们的知识结构，也引发了书籍形式的变革。在纽伦堡，木刻版画作为书籍插图的历史可以追溯至1493年。同年，哈特曼·舍德尔（HartmannSchedel） 的《纽伦堡编年史》在纽伦堡出版，印刷商安东·科贝格（Anton Koberger）委托画家米歇尔·沃尔格穆特（Michael Wolgemut） 和威廉·普莱登伍尔夫（WilhelmPleydenwurff） 为该书绘制插图，书中的地图和关于人物、物品、事件等的图片多达1809幅，在介绍国家、城市、皇帝、教宗和主教之余，还加入了天文学家、数学家和医学家，比如阿拉托斯（Aratus）、托勒密、坎帕努斯（Campanus）、拉齐的著作和生平等内容，充分体现出作者对科学的关注程度。这本书也成为15世纪最畅销的插图书之一，图文混排的形式和肖像画的风格被同时代的画家大量借鉴。此后，德意志的印刷书中开始出现整版的插图，譬如丢勒在1498年的《启示录》一书中也尝试过绘制整版的图像。从早期的书籍插图可以看到，它们大多是复制的或通用的刻板图像，无法描述现实中的主题，线条和结构比较简单，形象不够生动，缺乏解剖和透视，丢勒早期的木刻版画中也存在同样的问题。

1504年，丢勒为天文学家马沙阿拉·伊本·阿塔里（Mashāallāh Ibn Atharī） 的《論星球运动的科学》（De scientia motus or?bis） 一书绘制了22幅插图，作品的第一页是他为马沙阿拉设计的单页肖像木刻版画（图1）：一位戴帽子的长须长者坐在画面左侧，左手扶天体仪，右手持圆规，球体表面以辅助线画出基本轮廓，右上方有一个空白天体，代表马沙阿拉的天文学家身份，这应该是丢勒第一次在书籍中绘制圆规和几何图像。可以看出，丢勒已经注意到圆规和球体的必然联系，他绘制球体的技巧已相当成熟，但还不够了解明暗交界线的虚实画法，这说明他尚未完全把握结构、透视和空间的关系。实际上，丢勒的早期画作中普遍存在这个问题。马沙阿拉的形象与丢勒另一幅书籍插图（图2） 中的哲罗姆非常相似，丢勒试图通过衣褶的处理和手臂的动作来加强人物的立体感，但中轴线、肩臀线和重心线都显然缺乏合理的设计，导致手臂与手掌的关系无法成立，前臂和上臂的比例不正常，连带着画中的动物、植物和物件都存在比例失衡、纵深感及层次感匮乏的问题。以上情况表明此时的丢勒对人体结构不够了解，也尚未掌握透视法的基本要领，这些问题在德意志画家的作品中普遍存在，丢勒认为原因在于画家缺乏几何学教育和拉丁文知识，导致他们无法阅读古典作品中有关艺术和艺术家的内容。克里斯托弗·S. 沃德（Christopher S. Wood）指出，16世纪德意志艺术家出版的作品里都提到了方法、技术和透视法的问题，但“即使是丢勒，在前往威尼斯之前也无法摆脱作坊的心态”。

二、从抽象到具象：丢勒的几何学与测量法

德意志人对几何学和测量法有着浓厚的兴趣，原因是当时的人们普遍相信《智慧书》中所说的上帝是伟大的几何学家：“他用测量、数字和重量创造了所有事物。”这种信念在15世纪伴随新柏拉图主义的复兴而再次得到加强。此外，纽伦堡作为德意志最大的科学工具生产中心，几何学也是工匠制造机械钟和航海工具的必备知识。身为画工，圆规是丢勒测量时使用的主要工具，版画《忧郁I》中大天使的右手持有一把圆规，在《圆规直尺测量法》的第47页上有一把巨大的四臂圆规。据迈克尔·J. 索特（Michael J. Sauter） 考察，丟勒的天使形象可以追溯到14世纪的《道德圣经》（Biblemoralisée） 一书，在该书的插图中，上帝一只手托着宇宙，另一只手拿着圆规，因为《箴言》中记载着上帝用圆规创造了圆球体的宇宙：“他在海面上用圆规划出渊面。因此，圆规在丢勒眼里既象征着科学的测量方法，也蕴含了神圣的创造法则，正如他在自己的笔记中所言：“我会把我的理解建立在测量、数字和重量之上。”丢勒在作品中对几何学进行了具象化改造，赋予数学以文字、装置和图像这三种不同的认知形态。

在意大利文艺复兴艺术的诸多特点中，最引起丢勒关注的是意大利艺术品的精确度及其所使用的工具和方法。从青年时代开始，丢勒便注重学习数学知识，两次意大利之旅更是引发他在艺术创作上的重大转折。他尝试将古典原则融入北方绘画，同时也投入木刻版画的制作之中。帕梅拉·H. 史密斯（Pamela H. Smith） 认为，丢勒看到威尼斯画家雅各布·德巴尔巴里（Jacopo deBarbari） 使用几何学方法画出的两个男女裸体画像后大受震撼，激发了他学习透视法和研究人体比例的想法。丢勒于1506年重返意大利学习透视法，同时也注意收集数学著作和相关信息。在1506年10月13日写给朋友维利巴德·皮尔克海默（Willibald Pirckheimer） 的一封信里，丢勒表示自己“即将前往博洛尼亚去见一个人，那个人同意教给我透视法的秘密”。关于这位老师的身份，目前学界主要有两种推测。第一种推测是希皮奥内·德尔·费罗（Scipione delFerro） 或卢卡·帕乔利（Luca Pacioli），他们都是意大利数学家。费罗在1496至1526年间担任博洛尼亚大学数学教授，帕乔利则曾与达·芬奇合作完成了一部名为《神圣比例》（De divina proportione） 的著作，文字部分由帕乔利负责，插图由达·芬奇绘制。莫里茨·陶辛（Moritz Thausing） 率先指出，丢勒的《圆规直尺测量法》与《神圣比例》非常相似。《神圣比例》于1498年完成、1509年出版，因此丢勒很可能于1506年在意大利逗留期间与这位经常在意大利四处教授数学的帕乔利接触过，进而看过这部著作。

第二种推测是皮耶罗·德拉·弗朗切斯卡（Piero della Francesca）。潘诺夫斯基指出，丢勒曾经摹仿弗朗切斯卡的“箱子法”以钻研几何关系，同时他也创作了与弗朗切斯卡画作非常相似的几何练习图。弗朗切斯卡的著作《绘画透视法》（De ProspectivaPingendi） 在15至16世纪以抄本的形式流传，而丢勒的《人体比例四书》中出现了大量与此书相似的内容，说明丢勒应持有该书的抄本。《神圣比例》和《绘画透视法》都是在欧几里得《几何原本》的基础上写成的。《几何原本》在文艺复兴时期的再发现让意大利画家率先认识到几何学之于绘画的重要性，从而引发了创作观念的转变，正如保罗·劳伦斯·罗斯（Paul Lawrence Rose） 所言：“几乎不可能把数学的文艺复兴与普遍的文艺复兴切割开来，数学和几何的知识将会影响到每一个领域。”此后，视觉艺术不再是对现实的单纯摹仿或个人想象，而是在复兴古代知识的基础上寻找新的艺术理论。丢勒在意大利游历时不仅摹仿意大利画家的绘画风格和色彩笔触，更把学习重点放在透视法和方法论上，希望从几何学中习得适用于测量的数学知识。所以，丢勒的几何学不是数学家的几何学而是工匠的几何学，他的画作中出现了一种不同于意大利艺术的特殊风格，其构图形式和艺术语言都带有深刻的德意志烙印。

返回纽伦堡时，丢勒带回了一本在威尼斯购得的1505年欧几里得《几何原理》拉丁语印刷本。他在书本的封面底部画了自己的徽章，并写下“于1507年用一个达克特（ducat） 在威尼斯购得此书。阿尔布莱希特·丢勒”。丢勒不断丰富他的数学藏书，后来更是购入了雷格蒙塔努斯留下的部分书本。雷格蒙塔努斯逝世后，其藏书由学生伯恩哈德·瓦尔特（Bernhard Walther） 和纽伦堡市政府相继持有。1523年，纽伦堡市政府为了筹措资金建立慈善机构，决定将部分书籍出售，档案馆的记录显示：“在13日，我们以10个古尔登（gulden） 将一些瓦尔特的书本卖给了阿尔布莱希特·丢勒，这个价格是由维利巴德·皮尔克海默估算的。”据杰弗里·奇普斯·史密斯（JeffreyChipps Smith） 推测，丢勒拥有两本欧几里得的著作，一本是上文提及的1505年印刷本《几何原理》，另一本是从雷格蒙塔努斯藏书中获得的《几何原理》抄本，其他藏书包括阿尔伯蒂《论绘画》抄本、弗朗切斯卡《绘画透视法》抄本和维特鲁威《建筑十书》。马克斯·斯特克（Max Steck） 表示丢勒还拥有三本在纽伦堡出版的数学著作，分别是金匠汉斯·施穆特迈尔（Hans Schmuttermayer） 的《尖顶之书》（1490）、马特乌斯·罗伊泽尔（Matth?us Roriczer） 的《德语几何学》（1497） 和建筑师洛伦茨·拉切尔（Lorenz Lacher） 的《说明书》（1516），这三本书都与建筑学有关，包含一些几何学内容。

在掌握了一定的数学知识之后，丢勒于1525年撰写了他的第一部著作《圆规直尺测量法》。在前言中，丢勒把德意志青年画家比作在无知中肆意生长的大树，虽然富有天赋、饶有技艺，但是他们没有接受过基础的理论教育，完全凭借直觉和个人喜好进行创作，每当知识渊博的画家和真正的艺术家看到这些毫无计划的作品时，都会为他们的无知而失笑，所以丢勒把读者范围扩大到“画家、金匠、雕刻匠、石匠和木匠，以及所有想要了解几何学的人”。书名中的“圆规”（zirckel，现代德语是Zirkel） 和“直尺”（richtscheyt，现代德语是Richtscheit） 是纽伦堡工匠常用的工具。全书分为四卷：第一卷关于线条，介绍了线条的定义和组成；第二卷关于平面，讨论了多边形的构造、瓷砖图案和勾股定理；第三卷关于应用数学，包括柱子和纪念碑的设计和建造、日晷和字母的几何构造；第四卷关于柏拉图和阿基米德多面体，最后提到了如何用圆规和直尺解决著名的提洛难题。从内容可知，丢勒结合古希腊的数学知识，撰写了一部适合德意志工匠实际需要的作品。他在第一卷的标题里提到了欧几里得：“这本书对已经熟知欧几里得的几何学的人来说没有用处。因为这是一本只写给年轻人看的书，那些从来没有得到过正确指导的人。”尹相淑（Rangsook Yoon） 指出：“对于丢勒而言，几何学或者说测量的艺术，已经是用来构建形状的绘画工具，更重要的是，它是一种理性的认知工具，揭示出自然的秩序。”为了帮助工匠理解抽象的数学概念，丢勒以一种具象化的方式来改造几何学，让他们能在直观的意义上“看懂”数学。

长期以来，德语中严重缺乏专业的数学词汇，大部分数学著作都以拉丁语写成。丢勒在《圆规直尺测量法》的书名中使用“测量”（Messung） 一词时，实际上他的意思是“几何”（Geometria），后者在当时的德语中是一个相当陌生的词汇，人们熟悉的词语是“测量的艺术”（Messkunst） 或者“测量的知识”（Messkunde），他便以“测量”代替“几何”，Geometria仅出现在第一卷的标题之中。在翻译内容时，丢勒也注意到翻译不仅是词义的传递，也需要兼顾不同文化背景下的生活习俗，所以他会使用人们熟知的事物来进行具体解释，譬如“抛物线”（brenlini） 结合了“燃烧”（brennen） 和“线条”（linie），“双曲线”（gabellini） 则由“叉子”（gabel） 和“线条”组成。他也会使用工匠熟悉的工具或物品来取名，譬如“圆规线”（zirckel lini） 即“圆形”，“野猪的牙齿”（Eberz?hne） 表示圆弧所形成的角度。丢勒对艺术语言的影响是十分深远的，威廉·S. 赫克歇尔（William S. Heckscher） 说：“丢勒不得不创造出各种短语，并发明一种拥有大量词汇的技术性语言，以便用前路德时期的高地德语来表达拉丁语或意大利语中的观点。”

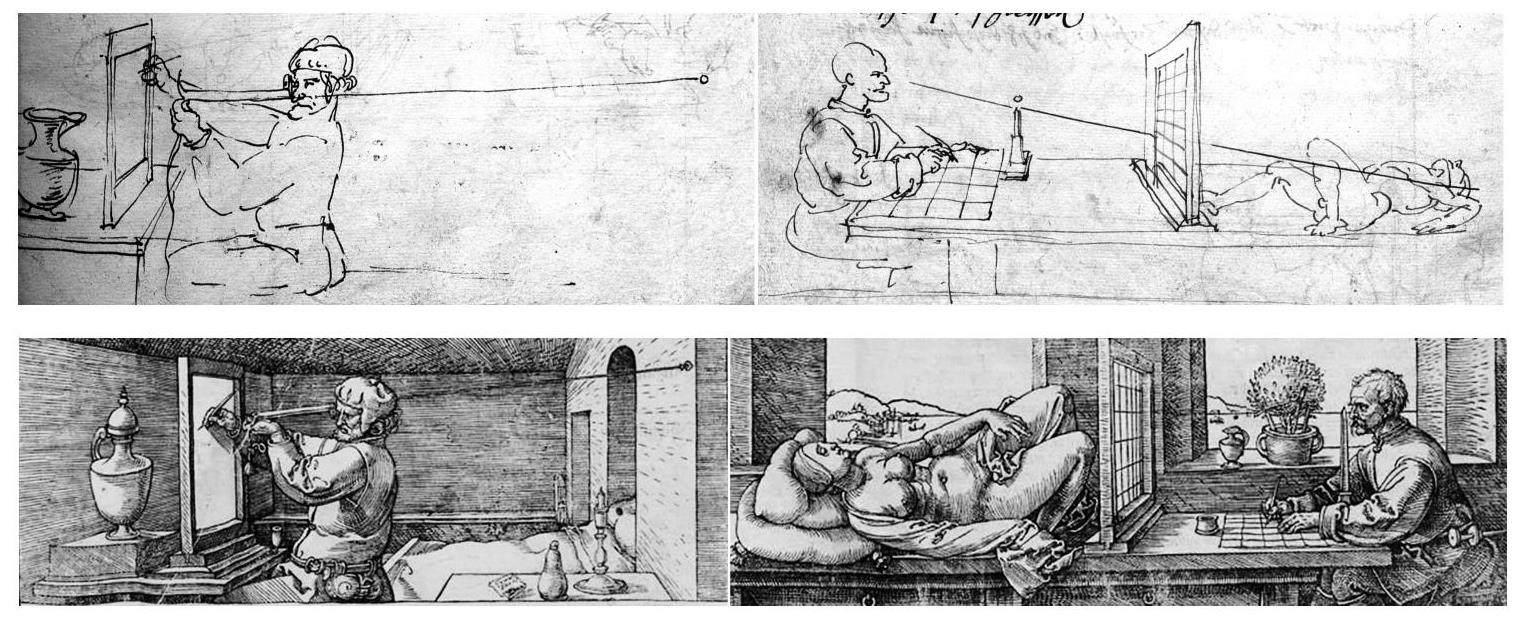
丢勒对数学的具象化处理还表现在透视法测量装置的设计上，他在自己持有的1525年初版《圆规直尺测量法》中留下了设计新装置的笔记。该书中有两个测量装置插图，分别为“男子测量图”和“鲁特琴测量图”，在后者的页面空白处，丢勒加上了“花瓶测量图”和“女子测量图”这两个设计草图（图3），二者与1538年修订版《圆规直尺测量法》中的装置十分相似（图4）。以“女子观测图”（图4右） 为例，丢勒的测量装置主要由五个部分构成：模特、阿尔伯蒂方格窗、观测器、观察者和方格纸。模特躺在枕头上，阿尔伯蒂方格窗上穿插表示X轴和Y轴的十字线，观察者通过观测器定位，然后在面前的方格纸上作画。弗里德里希·A. 基特勒（Friedrich A. Kittler） 认为，丢勒的透视法装置与布鲁内莱斯基的“小孔透视法”（camera obscura） 不同，更接近阿尔伯蒂在《论绘画》中提出的方格作画法，即在画家与对象之间放置一个绘有平面网格的玻璃板，将对象转换成确切的数字点，标记在同样绘有网格的画布之上。需要指出的是，阿尔伯蒂在描绘方格作画法的时候仅在文字里提到了这个方法，并没有将它以图像的方式表现出来，所以丢勒应该是第一位具象化方格作画法的画家。

与丢勒著作同时代的意大利透视法作品有帕乔利的《神圣比例》。帕乔利对透视法的看法主要有两点：一是应该把透视法纳入“四艺”（quadrivium） 之中，因为其研究的是比例问题，可以与几何、算术和天文学并列；二是把透视法视为理性的愉悦来源，认为“如果音乐满足的是自然感官之一的听觉，那么透视法满足的则是视觉，因为视觉是通向智慧的第一扇门，因此更加尊贵”。帕乔利还指出透视法不仅包含线性透视，也包含结构和颜色，因为“适当的距离和丰富的颜色会让人感到十分愉快”。丢勒在《圆规直尺测量法》第四卷的最后也介绍了透视法，他沿用了文艺复兴时期的艺术理念，即透视法基本等同于光学科学，是视觉、艺术和科学的结合，“我还会讲到光和影，以及如何把它们联系起來使用”。在给出数理化的测量方案之后，丢勒介绍了计算投影的更为简便的方案。如果将丢勒和帕乔利进行比较的话，可以发现丢勒对帕乔利的作品非常熟悉，同时又倾向于在帕乔利的基础上推进，直接回归古典时代去解答艺术测量中的疑难问题。

提洛问题是古希腊几何学的三大难题之一，也是使用圆规和直尺作图时必然会面临的数学问题，而丢勒在第四卷中介绍了该问题的起源，并给出了三个解决方案。他以切割立方体为引子，让工匠对立方体形态形成初步印象，然后道出提洛问题的起源。雅典人在遭遇瘟疫时向阿波罗求助，后者给他们出了一个数学难题，如果他们能在保持祭坛形状不变的情况下将祭坛的体积增加一倍，瘟疫便会消失。人们因无法解答该题而向柏拉图请教，柏拉图教导他们如何找到与两条不等长的给定线段成比例的两条直线，这样便可以成倍数放大立方体。丢勒表示这个方法可以用于木桶、盒子、轮子、箱子、图画等任何想要放大的东西，同时他也宣称从来没有人用德语解释过这个方法，而帕乔利在《神圣比例》中也没有言及提洛问题。

不同于帕乔利对“神圣比例”（即“黄金比例”） 的追求，丢勒在他的著作中没有提到“神圣比例”一词，显然他寻找的不是完美或神圣的比例。数学理论使他看到“美”是一个拥有多种形式的相对概念，数学方法让他掌握了更多图案样式和绘画技巧，他在人力所及范围内以纯粹的测量为基础，寻求艺术作品的新的可能性。丢勒从文字、装置和图像三个层面展开对几何学的具象化处理，将数学理论清晰、准确地呈现在德意志人面前，从而解决数学知识中难以理解的问题。他的作品也成为一种互动的绘画教学工具，激发和提高了工匠的抽象思维能力，不仅让他们能够快速掌握几何学的结构与应用，也使数学内化为德意志艺术设计的知识体系。此外，丢勒也拓宽了数学的应用范围，随后的艺术作品中开始大量出现多面体和几何符号图案，这些图案成为一种创新精神和形式美感的代表，深受大众喜爱。丢勒的美学观不仅影响了德意志人，也在16世纪中期逐渐传播至欧洲其他地区。

三、丢勒美学观的接受和影响

潘诺夫斯基指出，丢勒的艺术理论建立在“知识”和“实践”的基础之上。对丢勒而言，画家既要掌握自由七艺中的理论和科学知识，也要具备在作坊里操作的实践能力。此外，他也是最早认识到自己身处重要历史时刻的人，早在1523年的手稿中，丢勒便以“再生”（widererwaxsung）一词来描述当时文艺开始复兴的现象。他在1525年再次表示：“古代的书籍显示出希腊人和罗马人对艺术的尊崇和敬意，尽管它们后来失传或被隐藏了一千年，直到最近两百年，这些艺术才被意大利人重新发现。”

丢勒美学观有两个特点：一是正确的尺度，二是多样的文化。对丢勒而言，“艺术的尺度”也是“道德的尺度”，他希望通过提出正确的尺度，在艺术和道德上树立一个全新的标准，因为正确的测量会带来好的形式，这不仅体现在绘画上，也体现在所有事物上。在丢勒的笔记中有这样一段话：“我听说希腊七贤教导人们，测量存在于所有事物之中，无论是物质的还是道德的，它都是最好的。而且最高的神如此看重它，使用数字、重量和测量来创造所有被造物，毫无疑问，最接近测量的艺术和方法自然是最高贵和最可敬的。”同时，地理大发现让丢勒意识到人类文化的多样性。文化的多样性让画家难以用一种比例、一种标准来概括所有人类，虽然丢勒在《人体比例四书》中没有在面部轮廓图像上标注国籍或种族等词语，但他为不同类型的体态和面孔分别提供了测量方法，既有丰腴的、瘦削的，也有宽脸型、窄脸型，这体现出文艺复兴时期面相学研究的特性：不仅通过各种测量方法找到理想化、理论化的符号和范式，更要透过表象辨别出人类最深层的自我本质。在《人体比例四书》第三卷中，丢勒写道：“在人类种族中，我们会发现各种类型的人，根据肤色的不同，可以塑造出各种不同的形象。”丢勒的美学观在德意志、法国、意大利和尼德兰等地都得到广泛继承，正确的尺度和多样的文化成为衡量艺术作品价值的两个维度，譬如意大利人文主义者巴尔巴罗在写于16世纪下半叶的《透视法的实践》一书中没有提到帕乔利的“神圣比例”，而是采纳了丢勒的观点：“他为不同外貌专门设计了其他的测量方法，我这样说是为了避免人们以为这些方法是一成不变的。因此，我请学者们去阅读他的著作。”

丢勒美学的多样性不仅体现在文化上，在思想和方法上也有所创新，其解释体系融入了丰富的心理学元素，形象化的数学语言能够提高艺术概念的留存深度，难易程度不一的指导方案也能有效顾及不同人群的需要。一方面，从阿尔伯蒂到弗朗切斯卡，意大利人文主义者追求的是以正确的方法让人的眼睛看到物体的实际模样，这是几何学对艺术的贡献的一层含义。另一方面，几何学也赋予了艺术更为多元的结构和形式，人们的观察对象从物到人再到抽象概念，这不仅拓展了艺术的研究范畴，抽象结构本身也发展为一种新的艺术符号，让不可感知和不可触摸的事物拥有了现实的存在。如果将欧几里得、帕乔利、丢勒书中的图像进行对比的话，我们会发现《几何原理》的内容是纯粹解释性的数学图形，《神圣比例》在前者的基础上加入了柏拉图立方体、人脸侧面像和字母设计插图，让著作更富有绘画教学的实用意义，丢勒则让几何图像在视觉力量和美学价值上实现了新的突破。譬如在圆规的帮助下，丢勒的阿基米德螺线拥有多种变体，数学逻辑使几何图像获得了平衡且精确的细腻美感（图5），从而成为艺术研究的重要对象。

在16世纪，丢勒参与制作或独立完成的印刷书籍共19部，涉及数学、天文学、文学和宗教等多种题材，其中出版次数最多的是《圆规直尺测量法》，共10个版次。他的美学观对德意志图像艺术产生了深远影响，从16世纪30年代开始便有工匠在他的指导下运用几何原理撰写工艺类作品，这类作品一般被称为“艺术小手册”。如果对这个时期的艺术书籍加以分析的话，我们会发现至少有10部作品明显受到了丢勒的影响，其中8部为德意志作品：希罗尼穆斯·罗德勒《一本关于用圆规、直尺或尺子测量的艺术的精美实用的小册子和指南》（1531）、艾哈德·舍纳《模型比例和位置的指导》（1538）、奥古斯丁·希尔施福格尔《对几何学的真正和全面的指导》（1543）、赛巴德·贝哈姆《艺术和训练小册子》（1552）、海因里希·劳滕扎克《关于正确使用圆规和直尺，以及透视法，人和马匹比例的简短而全面的指导》（1564）、洛伦茨·斯特尔《几何学与透视法》（1567）、文策尔·雅姆尼策《正多面体透视图》（1568）、汉斯·伦克尔《透视法》（1571），这些著作在书名、内容和图像上都带有丢勒作品的印记。

丢勒的科学用语同样获得广泛应用，由于他使用“测量”来指代“几何”，“测量”也在很长一段时间里成为德语著作中的一个常用词语，尤其是描述借助工具进行测量这一步骤的时候，人们会像丢勒那样把透视法称为“测量的艺术”（Kunst des Messens）。丢勒的测量方法在德语作品中被反复提及，工匠试图在他的基礎上加以改良，譬如罗德勒的书中便出现了类似的观测装置。

从16世纪30年代开始，丢勒的著作被陆续翻译成拉丁语、法语和意大利语。《圆规直尺测量法》首先有的是拉丁语译本，译者约阿希姆·卡梅拉里乌斯（Joachim Camer?arius） 曾在维滕贝格大学跟随宗教改革家菲利普·梅兰希通（Philipp Melanchthon） 学习希腊语，后来前往纽伦堡新成立的阿吉迪恩文法学校（?gidien gymnasium） 担任希腊语和拉丁语教师。他翻译时重新把“几何”放进了书名，将这部拉丁语译本命名为“几何学原理”（institutionum geometricarum），此书于1532年在巴黎出版。卡梅拉里乌斯的翻译具有重要意义，拉丁语译作的出现使丢勒的读者群从德意志人扩展到各地的学者和数学家。在法语译本方面，丢勒的《人体比例四书》于1557年在巴黎出版，他的透视法装置也随之传播到了法国，萨洛蒙·得·高斯（Salomon de Caus） 在自己的著作中再现了丢勒的绳索测量法装置。在意大利语译本方面，柯西莫·巴尔托利（Cosimo Bartoli） 于1537年将卡梅拉里乌斯的拉丁语译本翻译成意大利语，但这份手稿没有正式出版。一般认为在欧洲最具影响力的意大利语译本是乔凡尼·保罗·加卢奇（Giovanni Paolo Gallucci） 1591年的译本，这本书曾两次在威尼斯出版，一直到巴洛克时期都持续发挥着重要影响。

在意大利，巴尔巴罗在传播丢勒艺术观的过程中起到了重要的推动作用。他在《透视法的实践》中多次提到丢勒，譬如该书的第六章来自《圆规直尺测量法》，第八章来自《人体比例四书》。他在举例阴影的投射时直接说明“我会用阿尔布莱希特·丢勒的例子结束这一部分”，使用的插图也来自《圆规直尺测量法》第四卷。在《透视法的实践》的全书插图中，有五幅来自《圆规直尺测量法》，三幅来自《人体比例四书》。此外，巴尔巴罗也会指出丢勒的不足之处，他认为丢勒在测量人体时过于细致，建议采用一种满足当前需要的中间方法，即按照人测量身体各部分的方法来计算。巴尔巴罗对丢勒作品的直接使用说明后者的著作在意大利地区已经具有深广影响，《透视法的实践》在威尼斯的两次出版（1568年和1569年） 也扩大了丢勒美学观的传播范围。进入17世纪后，丢勒的艺术观在尼德兰地区受到广泛关注，尼德兰在出版数量方面也成为仅次于德意志的丢勒作品出版地。从1603到1640年，在阿纳姆和阿姆斯特丹出版的丢勒书籍数量多达19部，他的作品全部被介绍到尼德兰，包括《圆规直尺测量法》《城镇、城堡和地面内的防御工事》和《人体比例四书》。第一本在尼德兰出版的丢勒著作是《圆规直尺测量法》（1603），次年便出版了《阿尔布莱希特·丢勒全集》，印刷商扬·扬森（Jan Jansen） 还为该书加上了一个新封面，注明“富有艺术才华的纽伦堡著名数学家、画家阿尔布莱希特·丢勒的所有作品”。扬森对书稿进行了重新排版，全书多达569页。从内容上来看，他选用的是丢勒作品的最新版本，譬如《圆规直尺测量法》的1538年修订版。汉斯·弗雷德曼在其著作《透视法》的前言中也表示：“阿尔布莱希特·丢勒是这些人中最受尊敬的，在我看来，他对自然界的本质研究得最为透彻，并在他的作品中把它表现得最为淋漓尽致……没有一个尼德兰人能做到这一点。”

人们在继承丢勒美学观的同时也会对他的写作提出异议，譬如罗德勒宣称丢勒的书籍“过于理论性和难以理解，只有特别有学问的人才能够使用它们”。近代早期的“艺术小手册”不仅接受了丢勒的观点，也在不同程度上对其加以改造，这主要反映在书籍尺寸和测量方法这两个方面。在书籍尺寸上，丢勒《圆规直尺测量法》（1538） 的大小是31.9×21.5×4.6厘米，而舍纳《模型比例和位置的指导》仅为17.7×13.7×1厘米，后者便于携带、价格便宜、易于存储、无需辅助性解释，可以直接为不同类型的艺术创作提供指导。在测量方法上，丢勒的人体比例图包含大量比例符号和数字，舍纳在自己的比例图中不仅简化了这些内容，也把结构线转移到人体外部的空间来讲解比例，可见前者注重的是测量的精确性，后者则更看重方法的实用性。“艺术小手册”出现后广受欢迎，舍纳和贝哈姆的作品在16世纪都曾四次再版，数学和艺术的结合也因此变得更加紧密。几何原理成为青年人提高绘画技艺的必备知识，也反映出近代早期欧洲以“自学”为导向的技术文献的兴起。

结语

从布鲁内莱斯基在圣母百花大教堂门旁举起镜子的那一刻起，数学规则便成为艺术的基础，艺术也被视为知识和科学的一种形式。在《人体比例四书》第三卷的最后，作为16世纪德意志画家代表人物的丢勒发出了他对美学的追问：“当我们问，如何才能创造出美丽的形象时，有人会说：跟随大众的口味。没有真正的知识，谁能给我们一个可靠的标准？”在丢勒看来，真正的知识是难以获取的，因为他认为一般的知识容易被削弱，真正的知识隐藏在自然之中，而数学是探索自然的最有效手段，也是终极真理的表述方式。因此，“如果通过几何学来验证我们的工作，并證明基本真理，那么全世界都会相信我们……能够做到这一点的人，理应被视为是拥有上帝赐予的天赋的大师”。

经过丢勒对几何学的具象化处理，数学成为一门适用于艺术创作的知识，而他本人也成为德意志融合艺术与科学的先行者。欧几里得在14世纪中期的复兴赋予了人们更多想象“空间”的能力，他们也继而要求在书籍、艺术作品和其他物质文化作品中展现出“空间”的存在。几何学作为一种媒介可以在个人空间和抽象空间之间搭建桥梁，把外部世界拆分为几何步骤进而定格在平面之上。正如约瑟夫·马谢克（JosephMasheck） 所言，阿尔伯蒂在提到方格作画法时仅将其视为一个虚构的、诗意的想象，丢勒却能够把它化为现实，这或许就是他捕捉空间的独特能力。

① Arnold Hauser，The Social History of Art， Vol. 2， New York and London： Routledge， 1990， pp. 54-55.

② Vgl. Albrecht Dürer，Underweysung der messung mit dem zirckel und richtscheyt， Nürnberg： Hieronymus Andreae，1525.

③ Vgl. Eberhard Schr?der，Dürer： Kunst und Geometrie， Basel： Springer， 1980.

④ Cf. Stephen Luecking，“Albrecht Dürers Celestial Geometry”，Math Horizons， Vol. 25， Issue 3 （2018）： 5-7; Al?exander Marr，“Ingenuity in Nuremberg： Dürer and Stabiuss Instrument Prints”，The Art Bulletin， Vol. 100， Is?sue 3 （2018）： 48-79.

⑤ “艺术小手册”自16世纪上半叶开始在德意志出现，书中包含大量富有装饰性的图片，读者可以摹仿图中的样式制造物品。Vgl. Julius von Schlosser，Die Kunstliteratur： Ein Handbuch zur Quellenkunde der neueren Kun?stgeschichte， Wien： A. Schroll， 1924， S. 243-245.

⑥ Dante Alighieri，Convivio， trans. William W. Jackson， Oxford： Clarendon Press， 1909， p. 111.

⑦ Leon Battista Alberti，On Painting， trans. Cecil Grayson， New York： Penguin Books， 2004， p. 35.

⑧ Lorenzo Valla，“The Glory of the Latin Language”， in James Bruce Ross and Mary Martin McLaughlin （eds.），The Portable Renaissance Reader， New York： Viking Press， 1953， p. 134.

⑨ Anthony Blunt，Artistic Theory in Italy， 1450-1600， Oxford： Oxford University Press， 1975， pp. 48-49.

⑩ Leonardo da Vinci，The Literary Works of Leonardo da Vinci， Vol. 1， ed. Jean Paul Richter， London： S. Low， Mar?ston， Searle & Rivington， 1883， p. 18.

Eberhard Isenmann，Die deutsche Stadt im Mittelalter 1150-1550： Stadtgestalt， Recht， Verfassung， Stadtregiment， Kirche，Gesellschaft， Wirtschaft， K?ln： B?hlau Verlag， 2014， S. 826-829.

Eugen Kusch，Nürnberg： Lebensbild einer Stadt， Nürnberg： Nürnberger Presse， 1951， S. 170.

Ernst Mummenhoff，“Freie Kunst und Handwerk in Nürnberg”， in Gesamtverein der Deutschen Geschichts ?und Altertumsvereine （Hrsg.），Korrespondenzblatt des Gesamtvereins der deutschen Geschichts ? und Altertumsvereine，Darmstadt： A. Klingelh?ffer， 1906， S. 105-120.

Johann Neud?rffer，Eine kurtze Verzaignus der Werckleute undt Künstler， Merkel Hs 4° 533， S. 23r， 23v， 24r， S.28r-v.

Wolfgang Schmid，Dürer als Unternehmer： Kunst， Humanismus und ?konomie in Nürnberg um 1500， Trier： Porta Al?ba Verlag， 2003， S. 7.

Lothar Schmitt，“Education and Learning among Sixteenth?Century German Artists”，Studies in the History of Art，Vol. 60 （2001）： 75.

Ernst Zinner，Regiomontanus： His Life and Work， trans. E. Brown， Amsterdam： North?Holland， 1990， pp. 82， 98，100.

See Owen Gingerich，“Copernicus and the Impact of Printing”，Vistas in Astronomy， Vol. 17 （1975）： 202.

Wolfgang von Stromor，“Hec opera fient in oppido Nuremberga Germanie ductu Ioannis de Moneregio： Regio?montanus und Nürnberg 1471-1475”， in Günther Hamann （Hrsg.），Regiomontanus?Studien， Wien： Verlag der ?ster?reichischen Akademie der Wissenschaften， 1980， S. 268.

阿尔伯蒂《论绘画》的印刷版直到1540年才在巴塞尔由纽伦堡数学家托马斯·費纳托尔（Thomas Vena?torius） 出版，后者是与丢勒共同阅读雷格蒙塔努斯《论绘画》抄本的成员之一。See Richard L. Kremer，“Text to Trophy： Shifting Representations of Regiomontanuss Library”， in James Raven （ed.），Lost Libraries：The Destruction of Great Book Collections since Antiquity， New York： Palgrave Macmillan， 2004， p. 81.

Hartmann Schedel，Liber chronicarum， Nürnberg： Anton Koberger， 1493， S. 70r， 113r， 189v， 193r.

Harry G. Aldis，“Book Illustrations”， in Paul A. Winckler （ed.），Reader in the History of Books and Printing， Engle?wood： Greenwood Publishing Group， 1983， p. 115， pp. 114-115.

丢勒在1505年之前为三部书籍绘制过插图，分别是《启示录》（1498）、《瑞典的毕哲的启示录》（1502）和《论星球运动的科学》（1504），前两部的图像皆以叙事人物为主题，第三部应该是丢勒第一次绘制带有科学性质的插图。

Klaus Robering，“Engineering and Mathematical Logic. Another‘Zilsel Casefrom the History of Computing”，in Donata Romizi， Monika Wulz and Elisabeth Nemeth （eds.），Edgar Zilsel： Philosopher， Historian， Sociologist， Ber?lin： Springer， 2022， p. 307.

See Christopher S. Wood，Albrecht Altdorfer and the Origins of Landscape， London： Reaktion Books， 2014， p. 285.

“Book of Wisdom 11：21”，The Second Tome of the Holie Bible Faithfully Translated into English， out of the AuthenticalLatin， Doway： Laurence Kellam， 1610， p. 358.“Proverbs 8：27”，The Second Tome of the Holie Bible Faithfully Translated into English， out of the Authentical Latin， p.279.

Albrecht Dürer，Dürers schriftlicher Nachlass： Auf Grund der Originalhandschriften und theilweise neu entdeckter al?ter Abschriften， Halle： Max Niemeyer， 1893， S. 316， S. 41， S. 297， S. 285.

Pamela H. Smith，The Body of the Artisan： Art and Experience in the Scientific Revolution， Chicago： The University ofChicago Press， 2004， p. 69.

Andrew Morrall，“Dürer and Venice”， in Larry Silver and Jeffrey Chipps Smith （eds.），The Essential Dürer， Phil?adelphia： University of Pennsylvania Press， 2010， p. 114， p. 114.

Moritz Thausing，Dürer： Geschichte seines Lebens und seiner Kunst， Leipzig： E. A. Seemann， 1876， S. 503.

Erwin Panofsky，“Die Perspektive als‘symbolische Form”， in Hariolf Oberer und Egon Verhezen （Hrsg.），Aufs?tze zu Grundfragen der Kunstwissenschaft， Berlin： Verlag Volker Spiess， 1980， S. 123.

Vgl. Albrecht Dürer，Hierinn sind begriffen vier bücher von menschlicher proportion zu nutz allen denen so zu diser kunst li?eb tragen， Nürnberg： Hieronymus Andreae， 1528.

See Paul Lawrence Rose，The Italian Renaissance of Mathematics： Studies on Humanists and Mathematicians from Pe?trarch to Galileo， Geneva： Librairie Droz， 1975， p. 2.

Cf.Euclidis Megarensis philosophi acutissimi Mathematici elementorum libri XV ex traditione Theonis， Bartholomeo Zamber?to Veneto Interprete， Venetiis： Tacuini， 1505. Wolfenbüttel， Herzog August Bibliothek， Rara， 22.5 Geom 2， http：//diglib.hab.de/drucke/22?5?geom?2f/start.htm？image=00003.

Rudolf Mett，Regiomontanus： Wegbereiter des neuen Weltbildes， Leipzig： B. G. Teubner， 1996， S. 136.

Verein für Geschichte der Stadt Nürnberg，Albrecht Dürers Umwelt： Festschrift zum 500， Nürnberg： M. Edelmann，1971， S. 85.

Jeffrey Chipps Smith，“The 2010 Josephine Waters Bennett Lecture： Albrecht Dürer as Collector”，RenaissanceQuarterly， Vol. 64， No. 1 （2011）： 13-15.

Max Steck，Dürers Gestaltlehre der Mathematik und der Bildenden Künste， Halle： Max Niemeyer， 1948， S. 124.

Albrecht Dürer，Underweysung der messung mit dem zirckel und richtscheyt， S. 8， S. 180-181， S. 199-200，S. 168， S. 159.

Michael Friedman，A History of Folding in Mathematics： Mathematizing the Margins， Berlin： Birkh?user， 2018， pp. 33， 38.

Vgl. Albrecht Dürer，Underweysung der messung mit dem zirckel und richtscheyt， S. 9， S. 8.

Rangsook Yoon，“DürersUnderweysung der Messung and the Geometric Construction of Alphabets”， in IngridAlexander?Skipnes （ed.），Visual Culture and Mathematics in the Early Modern Period， New York and London： Rout?ledge， 2017， p. 78.

有学者认为丢勒在写作过程中可能向好友皮尔克海默请教过翻译问题，因为他的教育程度不足以让他独立完成专业术语的转化。皮尔克海默曾前往意大利学习，返回纽伦堡后不仅建立了德意志最大的私人图书馆，还把托勒密的《地理学》翻译成德语。Vgl. Helmut Neuhaus，Nürnberg： Eine europ?ische Stadt in Mittel?alter und Neuzeit， Nürnberg： Selbstverlag des Vereins für Geschichte der Stadt Nürnberg， 2000， S. 146.

See Andrea Bubenik，“The Shape of Things to Come： Dürers Polyhedron”， in Andrea Bubenik （ed.），The Persis?tence of Melancholia in Arts and Culture， New York and London： Routledge， 2019， p. 90.

诺姆·安德鲁斯首次研究了丢勒本人持有的《圆规直尺测量法》1525年版，并将丢勒在该书上留下的笔记与1538年版进行了详细的对比分析。Cf. Noam Andrews，“Albrecht Dürers personalUnderweysung der Mes?sung”，Word &Image， Vol. 32， Issue 4 （2016）： 409-429.

Friedrich A. Kittler，“Perspective and the Book”， trans. Sara Ogger，Grey Room， No. 5 （2001）： 45-47.

Reinhold Martin，“Points of Departure： Notes Toward a Reversible History of Architectural Visualization”， inSabine Ammon and Remei Capdevila?Werning （eds.），The Active Image： Architecture and Engineering in the Age ofModeling， Berlin： Springer， 2017， pp. 6-7.

Luca Pacioli，Divina proportione， die Lehre vom goldenen Schnitt， Wien： C. Graeser， 1896， S. 40， S. 40.

Erwin Panofsky，The Life and Art of Albrecht Dürer， Princeton： Princeton University Press， 1955， p. 242.

Berthold Hinz，Albrecht Dürer： Supplement zur‘Menschlichen Proportion.Die Dresdner Handschrift （1523）， Berlin： DeGruyter， 2016， p. 136.

Albrecht Dürer，Hierinn sind begriffen vier bücher von menschlicher proportion zu nutz allen denen so zu diser kunst lieb tra?gen， S. 219.

Daniele Barbaro，Daniele BarbarosPerspective of 1568， trans. Kim Williams and Cosimo Monteleone， Cham：Birkh?user， 2021， p. 362， pp. 337， 357， p. 358.

数据来自“VD 16”数据库，http：//www.vd16.de。

Verzeichnis der im deutschen Sprachbereich erschienenen Drucke des 16. Jahrhunderts （VD 16）， www.vd16.de.

Kirsti Anderson，The Geometry of an Art： The History of the Mathematical Theory of Perspective from Alberti to Monge，New York： Springer， 2007， p. 224.

Hieronymous Rodler，Eyn sch?n nützlich büchlin und underweisung der kunst des Messens， mit dem Zirckel， Richtscheidtoder Lineal， Simmern： Hieronymus Rodler， 1531， S. 55.

Matthias Asche，“Die Universit?t Marburg?Institutionen und Strukturen einer typischen frühneuzeitlichen Lande?suniversit?”， in Wolf?Friedrich Sch?ufele （Hrsg.），Reformation der Kirche?Reform der Bildung： Die Universit?t Marburgund der reformatorische Bildungsauftrag， Münster： Waxmann Verlag， 2020， S. 153.

Cf. Albrecht Dürer，Pictoribus， fabris erariis ac lignariis quatuor his suarum institutionum geometricarum libris， lineas， superfi?cies et solida corpora tractavit， trans. Joachim Camerarius， Paris： Chrestien Wechel， 1532.

Cf. Albrecht Dürer，Les quatre livres de la proportion， des parties et pourtraicts des corps humains， trans. Louis Meigret，Paris： Charles Périer， 1557.

Salomon de Caus，La Perspective， London： R. Barker， 1611， pp. 61， 105.

Judith Bryce，Cosimo Bartoli （1503-1572）： The Career of a Florentine Polymath， Geneva： Librairie Droz， 1983， pp.177-178.

Cf. Albrecht Dürer，Della simmetria dei corpi humani， libri quattro， trans. Giovanni Paolo Gallucci， Venezia： Domeni?co Nicolini da Sabbio， 1591.

数据来自“通用短标题目录”（Universal Short Title Catalogue） 数据库，https：//www.ustc.ac.uk/。

Cf. Jan Jansen，Opera Alberti Dureri. Das ist， Alle Bücher des weitberühmbten und Künstreichen Mathematici und MahlersAlbrechten Durers von Nürenberg， Arnhem： Jan Jansz， 1604.

See Hans Vredeman，Perspective， Leiden： Hendrik Hondius， 1605， p. 11.

Vgl. Hieronymous Rodler，Eyn sch?n nützlich büchlin vnd vnderweisung der kunst des Messens， mit dem Zirckel， Richts?cheidt oder Lineal， Simmern： Hieronymus Rodler， 1531， S. aiir.

Erhard Sch?n，Unterweisung der proportion und stellung der possen， Nürnberg： Christoph Zell， 1542， S. 26.

Jaya Remond，“Artful Instruction： Pictorializing and Printing Artistic Knowledge in Early Modern Germany”，Word &Image， Vol. 36， Issue 2 （2020）： 101-104.

Vgl. Albrecht Dürer，Dürers schriftlicher Nachlass： Auf Grund der Originalhandschriften und theilweise neu entdeckter al?ter Abschriften， S. 222， S. 222.

Michael J. Sauter，The Spatial Reformation： Euclid Between Man， Cosmos， and God， Philadelphia： University of Penn?sylvania Press， 2019， p. 26.

Joseph Masheck，Modernities： Art?matters in the Present， University Park： Pennsylvania State University Press， 1993，p. 17.

作者单位中国人民大学历史学院

责任编辑吴青青