基于离散元的GFRP筋-水泥土界面黏结特性分析*
2024-01-11张根宝何仕林陈昌富徐长节毛凤山
张根宝 何仕林 陈昌富 徐长节 毛凤山
(①湖南城市学院土木工程学院,益阳 413000,中国)(②湖南大学建筑安全与节能教育部重点实验室,长沙 410082,中国)(③湖南大学土木工程学院,长沙 410082,中国)(④城市地下基础设施结构安全与防灾湖南省工程研究中心,益阳 413000,中国)(⑤江西省地下空间技术开发工程研究中心,南昌 330013,中国)
0 引 言
加筋水泥土桩锚结构在软土地基加固和建筑基坑支护等领域应用逐渐增多,应用效果获得了业界的认可(孙超等,2018; 王炳等,2019)。工程中通常用钢筋作为加筋水泥土结构的加筋体,由于水泥土适用地层的土体常具有一定的腐蚀性,导致钢筋锈蚀,从而影响结构的使用寿命。相比于钢筋,GFRP(玻璃纤维增强塑料)筋具有抗腐蚀性能好、抗拉强度高、抗磁性能好、重量轻等优点(朱鸿鹄等,2012),将GFRP筋替代钢筋作为加筋体具有重要的应用前景。
实际工程中,锚固系统失效通常是由岩土体与锚固体界面产生的滑移破坏导致的(尤春安等,2009),加筋水泥土结构的承载性能主要取决于水泥土与加筋体的界面黏结性能。由于缺少关于水泥土与GFRP筋界面黏结性能的设计准则,将GFRP筋作为加筋体的加筋水泥土结构还未在实际工程中得到应用。因此,开展GFRP筋-水泥土界面黏结性能的研究具有重要的理论意义和应用价值。
目前,大部分学者都是通过现场及室内拉拔试验来研究筋体-岩土体界面的黏结性能。洪成雨等(2017)通过现场拉拔试验指出土钉表面粗糙度、灌浆压力及上覆土压力是影响界面摩阻力的关键参数,叶新宇等(2021)通过室内模型试验指出注浆压密效应是影响土钉抗拔性能的重要因素。张冠军等(2002),于宁等(2004),Chen et al.(2018)通过室内拉拔试验对筋体-水泥土界面的黏结性能进行了研究,指出水泥土的抗压强度、掺入比、龄期以及筋体的表面形态对筋体-水泥土界面的黏结性能有重要影响。关于GFRP筋在不同黏结介质中的黏结性能研究主要集中在混凝土、风化岩(白晓宇等,2018,2020)以及砂浆(薛伟辰,2005; 张景科等,2014)等方面,着重考虑了GFRP筋的直径、肋距等表面形态特征对界面黏结强度的影响(郝庆多等,2008; 罗小勇等,2015),并基于回归分析建立了界面黏结滑移模型(陆新征等,2005; Chen et al.,2020)。关于GFRP筋在水泥土介质中黏结性能的研究报道较少,主要通过水泥土中GFRP筋拉拔试验得到界面黏结滑移曲线,并基于拉拔破坏后筋体附着水泥土的形态特征对筋体-水泥土界面承载过程进行初步分析(陈昌富等,2019; Chen et al.,2020)。
上述研究的关注点侧重于筋体-岩土体界面的黏结强度发展规律,对于界面黏结强度发挥机制,即界面黏结滑移过程中黏结体应力变形和剪切带演化等,未做深入分析。GFRP筋-水泥土界面的黏结性能涉及到水泥土与GFRP筋两种材料之间的复杂相互作用,通过室内或现场的拉拔试验仅能在宏观上获得GFRP筋-水泥土的界面黏结滑移曲线,无法从细观上获取GFRP筋-水泥土黏结滑移过程中筋体与土体共同受力变形的特征。数值仿真方法可以从内部揭示材料相互作用机制,能够为试验研究提供有效补充。因此,已有学者采用数值模型对结构体-岩土体界面承载机理进行了研究,主要包括桩-土界面(钱建固等,2015)、加筋体-混凝土界面(王海龙等,2011)以及岩石锚杆界面(车纳等,2018; 方威等,2018)等。大部分数值模拟是采用有限元法、有限差分法等方法,无法准确描述界面的接触关系以及变形破坏的细观机理。离散元法能有效地模拟材料的宏细观力学响应及变形破坏过程(Potyondy et al.,2004),但单元数量受到计算效率的限制。国产离散元软件MatDEM依靠图形处理器在平衡单元数量和计算效率方面性能优良,成为岩土和地质工程领域离散元模拟的重要工具(刘春等,2020)。然而,有关GFRP筋-水泥土界面黏结特性方面的数值仿真研究,目前尚未见文献报道。
为此,本文采用离散元数值模拟方法,对GFRP筋在水泥土中的拉拔试验和界面黏结滑移响应进行了全过程数值仿真,重点考察了界面黏结滑移过程中界面位移场演化、剪切带发展规律以及胶结破坏演化等在室内试验中无法获取的关键特征和信息,从细观上揭示了GFRP筋-水泥土界面黏结滑移破坏机制,并通过参数分析研究了筋体形态特征对界面黏结特性的影响规律。
1 水泥土中GFRP筋拉拔试验离散元模拟
1.1 离散元模型建立
为深入分析GFRP筋-水泥土界面黏结滑移特性,采用国产矩阵离散元软件MatDEM对陈昌富等(2019)开展的水泥土中GFRP筋单元体拉拔试验进行数值模拟。单元体试验(陈昌富,2019)中所制备的单元体试样如图1所示,基于单元体试样的对称性,建立了其二维离散元模型,如图2所示。

图1 单元体试样
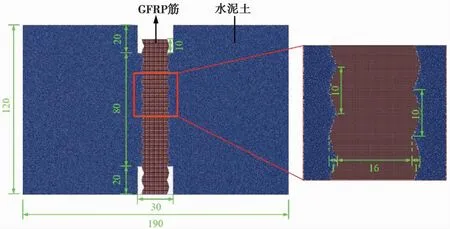
图2 水泥土中GFRP筋拉拔试验离散元模型(单位:mm)
模型中间部分为带肋GFRP筋,筋体直径为16mm,肋间距与肋高分别为10mm及1mm,筋体周围为水泥土,水泥土试样直径为190mm,高为120mm,GFRP筋与水泥土的黏结长度为80mm。采用MatDEM中的Toolcut函数切割堆积模型来实现筋体肋的外轮廓模拟。颗粒间采用线弹性接触模型,单元平均粒径为1.5mm(颗粒粒径介于1.23~1.77mm),总数为323617个,其中:水泥土单元数为262472个,GFRP筋单元数为40356个,边界单元数为20789个。
1.2 材料设置
本文离散元模型的力学性质主要受单元的接触模型和宏细观力学参数控制。在MatDEM中,模型材料参数的输入值为5个宏观力学参数,包括杨氏模量E、泊松比v、抗压强度Cu、抗拉强度Tu和内摩擦系数μi。对于线弹性接触模型,单元的5个细观力学参数(法向刚度Kn、切向刚度Ks、断裂位移Xb、初始抗剪力Fs0和摩擦系数μp)可由5个宏观力学参数以及单元直径d通过(Liu et al.,2017)给出的转换公式计算得到。转换公式如下:
(1)
(2)
(3)
(4)
(5)
由于随机堆积模型的力学性质通常会比设定值小,因此,为获得力学性质更准确的材料,需要对材料参数进行自动训练。材料训练的过程为:先用设定的材料参数来建立随机堆积模型; 然后对堆积模型进行单轴压缩、抗拉强度、抗压强度测试,获得堆积模型的实际弹性模量和强度; 再通过实测值和设定值的比率反复调整细观参数,直至各材料力学性质收敛于设定值。
参考本课题组已开展的水泥土中GFRP筋拉拔试验所采用实际材料的物理力学性质(陈昌富等,2019),本文数值建模过程中设置的水泥土与GFRP筋的宏观力学参数如表1所示,通过材料训练及转换公式得到的水泥土与GFRP筋的细观力学参数见表2。

表1 水泥土与GFRP筋的宏观力学参数

表2 水泥土与GFRP筋的细观力学参数
1.3 模型平衡及荷载施加
对模型赋予材料参数后,模型中各单元间受力会发生急剧变化。为了防止模型由于骤然增加的单元间应力而炸裂,需要对模型进行强胶结平衡,将单元间赋予足够大的抗拉力和初始抗剪力,随后再进行标准平衡,将系统的能量迅速耗散。对模型不断进行胶结与平衡,直至单元运动达到稳定状态,从而获得稳定的数值模型来满足高精度的模拟。
模型加载方案与试验(陈昌富等,2019)保持一致。采用位移控制的准静态加载方式,对GFRP筋顶部施加缓慢速度来模拟位移荷载的施加,拉拔速度为0.01mm/时间步,直至筋体拔出长度为20mm时停止模拟,为满足较高精度的数值模拟,需要进行足够多的迭代计算,本文模型中设置迭代计算次数为10万次。
2 模拟结果与分析
2.1 荷载-位移曲线
图3为GFRP筋-水泥土拉拔试验荷载-位移曲线的数值模拟结果与试验(陈昌富等,2019)结果对比,两者变化趋势基本一致,拉拔荷载先随着位移的增加而增大,达到峰值点后呈现波动式衰减。离散元模拟的荷载-位移曲线显示的峰值点荷载与试验记录的峰值点荷载非常接近,都处于8~10kN之间。然而,峰值点后波动式衰减段的荷载值却略高于试验值,这可能是由于离散元模型中的水泥土颗粒单元与实际土颗粒在力学行为与形状上存在差异性所导致的,比如试验中筋体周围存在部分土颗粒被剪碎的情况,但数值模型中模拟水泥土的颗粒单元无法破碎。
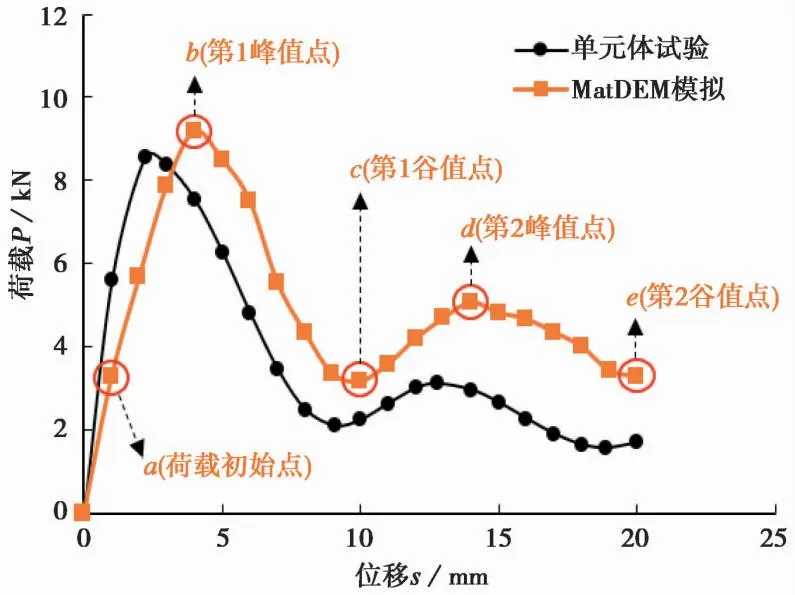
图3 荷载-位移曲线
另一方面,从图3中可观察到荷载-位移曲线上存在5个荷载特征点a、b、c、d、e,可依次定义为荷载初始点、第1峰值点、第1谷值点、第2峰值点以及第2谷值点,分别对应GFRP筋拔出位移为1mm、4mm、10mm(一个肋间距)、14mm、20mm(两个肋间距)时的筋体端部荷载。
2.2 界面位移场演化分析
图4为GFRP筋-水泥土拉拔试验模拟结束后(s=20mm)的模型位移云图。从图中可以看出,筋体拔出对周围水泥土的位移影响范围主要发生在两者界面处,靠近筋体上部的水泥土位移影响范围呈现出一个倒锥形喇叭口,这与试验(陈昌富等,2019)观察一致。

图4 拉拔结束后水泥土位移云图
为了进一步从细观上研究GFRP筋-水泥土的界面黏结滑移破坏机制,对研究区域进行聚焦,选取图4中黄色矩形框对应的界面处3个肋距长度范围来进行研究,提取荷载-位移曲线上不同拉拔位移下的GFRP筋-水泥土界面位移场演化情况,如图5所示。
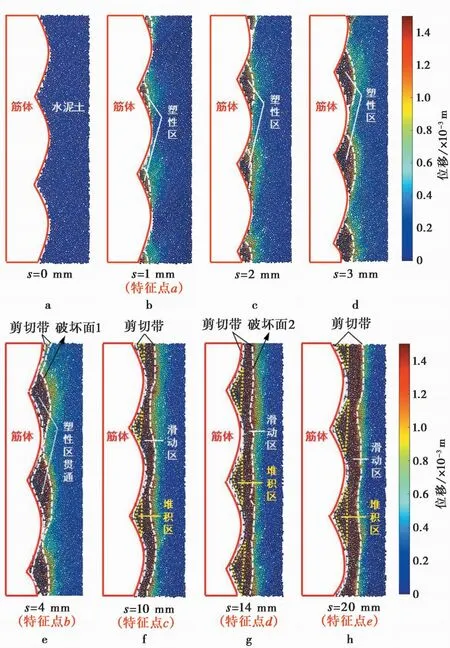
图5 不同拉拔位移下界面附近水泥土位移场演化过程
图5a~图5e是水泥土凸起部分的塑性区由初步形成发展至贯通的过程,当筋体拔出至s=1mm时,此时筋体与水泥土近似处于弹性平衡状态,筋体受拉时肋凸起部分对周围水泥土有挤压作用,在水泥土凸起部分开始形成塑性区(图5b); 随着筋体继续拔出,水泥土凸起部分的塑性区不断扩大,直到筋体拔出至s=4mm时,塑性区贯通整个水泥土凸起部分,界面处开始发生剪切破坏形成破坏面1(图5e),在云图中表现为位移量达到1.5mm的紫色区域和位移量不足1mm的黄绿色区域分界线,此时曲线上荷载达到最大值。图5e~图5h为水泥土凸起部分的塑性区贯通后进入塑性变形阶段并与筋体发生相对滑移的过程,当s>4mm时,筋体与水泥土开始发生相对滑移,界面处滑动的水泥土颗粒形成滑动区并沿着破坏面1移动,并填充在筋体相邻肋间区域伴随筋体向上移动,并由于滑动产生挤压导致部分堆积水泥土再次附着在筋体肋间表面形成堆积区(图5f黄色虚线区域)。堆积区水泥土颗粒的增加导致界面处的摩阻力及机械咬合力减弱,从而使得筋体与水泥土的黏结作用持续减弱,直至筋体拔出至s=10mm时,曲线上荷载降低至第1谷值点; 当拉拔位移s=14mm时,界面处发生第2次剪切破坏形成破坏面2(图5g),此时曲线上荷载上升至第2峰值点。需要注意的是,与第1次剪切破坏相比,第2次剪切破坏形成的塑性区及剪切破坏面较小,所以曲线上拉拔荷载第2次上升的幅度要小于第1次; 当s>14mm时,滑动区沿着破坏面2移动,直至筋体拔出至20mm时,由于肋前堆积区土颗粒的增加(图5h),筋体与水泥土的黏结作用再次减弱,曲线上荷载下降至第2谷值点。
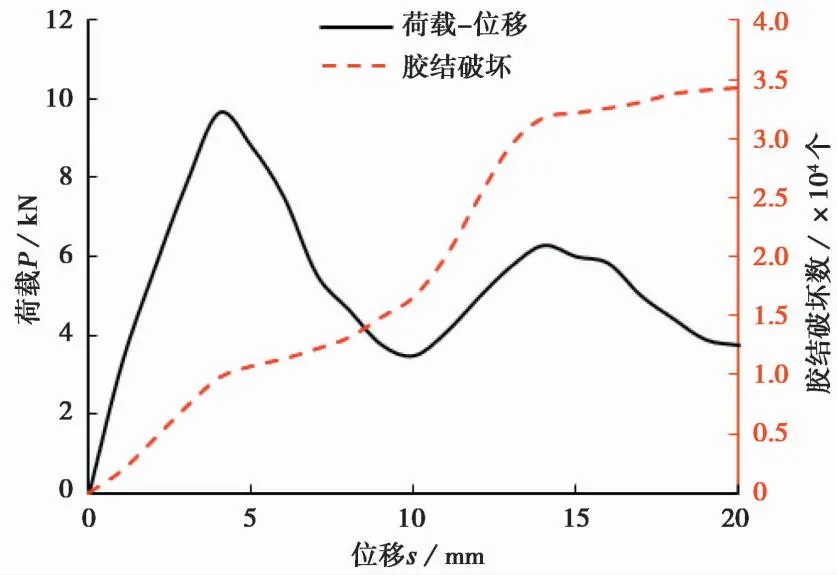
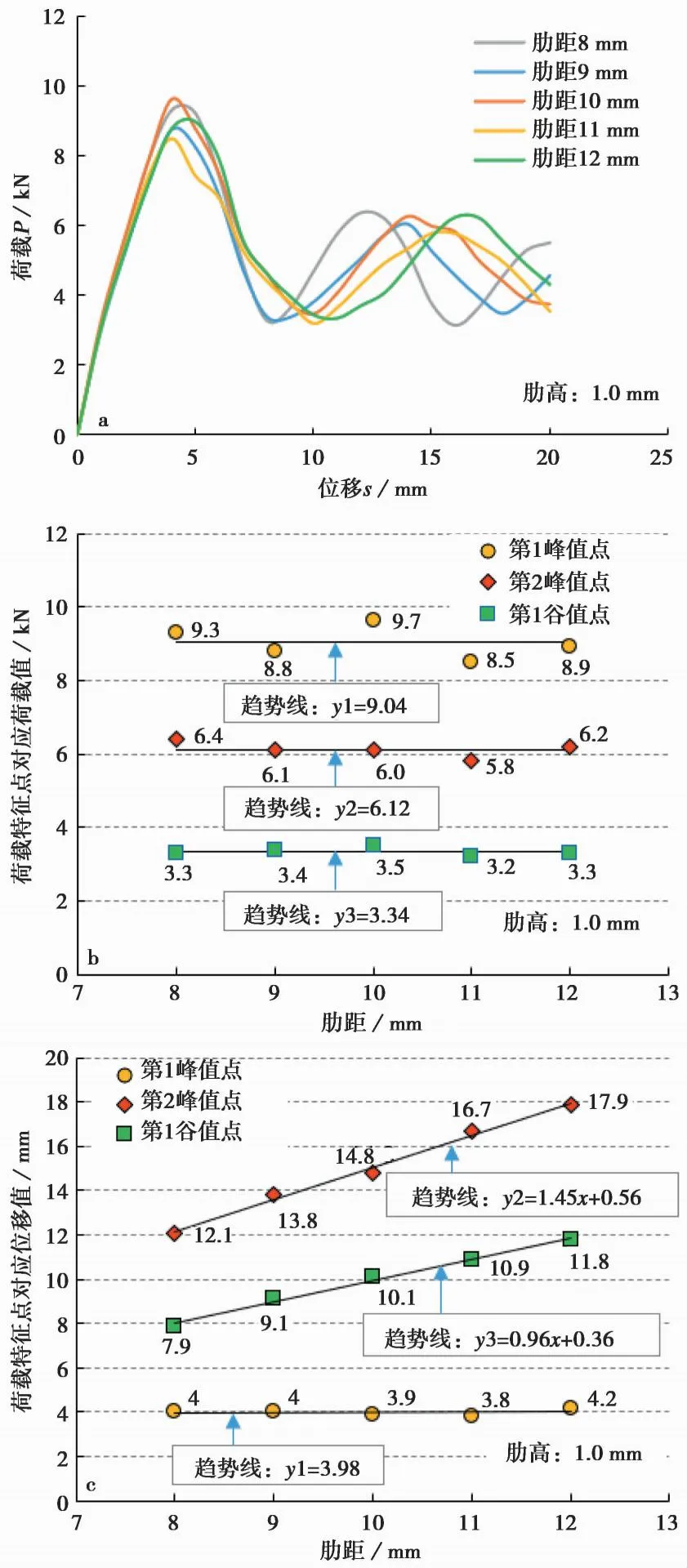
由上述分析可知,在界面黏结滑移过程中筋体附近水泥土发生了两次剪切破坏,水泥土内剪切带演化过程可以通过剪切颗粒数变化来刻画,如图6所示。从图中可以发现,剪切颗粒数随拉拔位移的增加总体呈上升趋势,在拉拔初期(0mm 图6 不同拉拔位移下剪切颗粒数的变化 本文数值模型中水泥土颗粒间是通过胶结作用连接的,由以上位移场演化分析可知,随着筋体的拔出会引起周围水泥土颗粒的滑移,同时,相邻的水泥土颗粒间会发生相对位移。当单元间法向相对位移超过断裂位移Xb时,相互胶结的颗粒单元间将发生胶结破坏并生成裂隙。 GFRP筋体附近水泥土变形破坏的发展过程可以通过离散元模型中颗粒胶结破坏情况反映。MatDEM中记录了拉拔过程模型中胶结破坏的变化情况,如图7所示。 图7 不同拉拔位移下胶结破坏演化 从图中可以看出,胶结破坏区域随着拉拔位移的增加逐渐从GFRP筋-水泥土界面处沿径向朝两侧土体扩展; 胶结破坏区域在拉拔端一直往斜上方向发展,在自由端则逐渐呈斜上转斜下的趋势。 图8为拉拔荷载和胶结破坏数随拉拔位移的变化关系。结合图7和图8可以发现,胶结破坏曲线与荷载-位移曲线都存在分段现象,且两者之间存在对应关系:在拉拔初期(s=1mm),水泥土与筋体开始产生挤压作用,在界面处有零散的胶结破坏特征; 随着拉拔位移的增加,荷载位移曲线基本呈线性关系,胶结破坏数增加也较快; 当拉拔荷载上升至第1峰值时(s=4mm),零散的胶结破坏点逐渐在界面处扩展成连续的破坏面并形成裂纹,随后拉拔荷载逐渐降低,胶结破坏数增长减慢; 当s>10mm时,胶结破坏由界面处逐渐向两侧土体扩展,拉拔荷载再一次上升; 直至s=14mm时,扩展至水泥土中的胶结破坏数上升幅度不再明显,拉拔荷载再次降低,此时胶结破坏曲线趋于水平。 图8 拉拔荷载和胶结破坏数随拉拔位移的变化关系 为了进一步分析GFRP筋体形态特征对筋土界面承载特性的影响,基于试验所用的GFRP筋的形态参数,结合实际GFRP筋产品参数可选范围,分别在10mm肋距和1mm肋高情形下,变化筋体肋高和肋距,考察GFRP筋体与水泥土界面黏结滑移响应的演化规律。 筋体肋高为1mm,不同肋距下GFRP筋体单元在水泥土中拉拔荷载-位移曲线变化,如图9所示。由图9a可知,肋距变化对荷载位移曲线的影响主要体现在残余段,特别是残余段荷载峰值点和谷值点对应的拉拔位移,而对荷载峰值和谷值的影响则并不明显。图9b为不同肋距下荷载特征点对应荷载值的变化趋势。可以看到,肋距对特征点荷载值影响很小,荷载值随肋距变化趋势近似为水平线,荷载第1峰值点都在9.04kN上下,荷载第2峰值点荷载都在6.12kN附近,荷载第1谷值点都在3.34kN附近。图9c为荷载峰值点和谷值点对应拉拔位移随肋距变化趋势图。可以发现,荷载特征点对应位移值均与肋距成线性增长关系,荷载第1峰值对应位移增长率为0,荷载第1谷值对应位移增长率为0.96,荷载第2峰值对应增长率为1.45。 图9 肋距对界面黏结特性的影响 结合前文界面位移场演化分析,不难发现产生上述肋距影响的主要原因在于,筋体肋距只影响界面附近塑性区的发展速率,而对塑性区的发展规模影响较小,具体表现为图5e中塑性区贯通区域并未完全调动肋间土体,图5g中滑动区只涉及筋体长度,两者均未受到肋距的直接影响。 图10为肋距为10mm时不同肋高下GFRP筋体单元在水泥土中拉拔荷载-位移曲线对比。从图10a可以看出,肋高变化主要对荷载特征点对应荷载值影响显著,对荷载特征点对应位移值影响很小。值得说明的是,如图10b所示,荷载峰值随着肋高增加而增大,当肋高为2.0mm时达到最大(荷载第1和第2峰值分别为11.6kN和9.2kN),继续增大肋高,则会引起荷载峰值降低。荷载谷值也有类似变化趋势。说明在恒定肋距下,存在最优肋高,可以最大程度调动界面黏结强度。从图10c可知,荷载特征点对应位移对肋高变化不敏感,均分别保持在4mm、1倍肋距、1.5倍肋距和2倍肋距附近。 图10 肋高对界面黏结特性的影响 肋高所产生的影响依旧可从界面附近塑性区发展规模的角度分析,肋高直接决定了图5e中土体贯通塑性区的高度和图5g中堆积区土楔的体积,前者表现为胶结破坏颗粒数量大小,后者则表现为拉拔随动土体质量大小。 本文通过建立GFRP筋-水泥土拉拔试验的二维离散元数值模型,对GFRP筋-水泥土界面黏结滑移破坏全过程进行数值模拟,结合荷载-位移曲线、界面位移场演化、剪切带发展及胶结破坏演化和参数分析,深入研究了GFRP筋-水泥土界面黏结滑移破坏机制。得到以下结论: (1)数值模拟得到的荷载-位移曲线可分为上升段、下降段、残余上升段、残余下降段4个阶段,拉拔荷载先随着位移的增加而增大,达到峰值点后呈现波动式衰减,与试验结果基本一致,验证了本文数值模型的可靠性。 (2)GFRP筋-水泥土界面黏结滑移全过程会发生两次剪切破坏,当拉拔位移为4mm时生成破坏面1,随后发生第1次剪切破坏,当拉拔位移至10mm(一个肋间距)时生成破坏面2,随后发生第2次剪切破坏,这也造成了拉拔荷载经历两次上升与下降。 (3)剪切带内剪切颗粒数随拉拔位移的增加总体呈上升趋势,在拉拔初期上升趋势相对明显,随着滑动区的发展上升趋势逐渐减缓。 (4)胶结破坏点初次形成于GFRP筋-水泥土界面处,随着拉拔位移的增加逐渐从界面处沿径向往两侧水泥土扩展,胶结破坏曲线与荷载-位移曲线都存在分段现象,且两者之间存在对应关系。 (5)GFRP筋体肋距主要影响荷载特征点对应位移值,对荷载峰值和谷值影响很小; 筋体肋高对荷载峰值和谷值影响显著,且在恒定肋距下,存在最优肋高可最大程度调动界面黏结强度。 本文研究尚存在一定局限性,一方面,试验中GFRP筋体的肋是呈三维螺旋状上升的,其引起的非对称效应影响需要进行三维数值仿真研究; 另一方面,GFRP筋-水泥土界面黏结性能受到多种因素影响,如围压、筋体直径以及水泥土配比和龄期等,对应的影响机制拟在后续工作中进一步研究。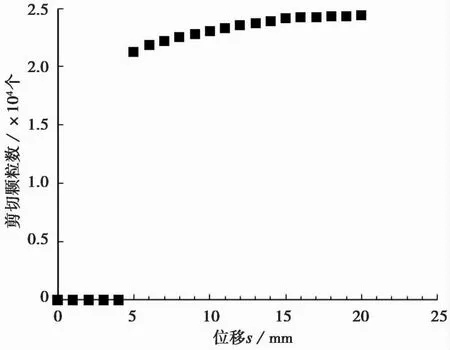
2.3 胶结破坏演化分析

3 界面黏结滑移特性参数分析
3.1 肋距的影响
3.2 肋高的影响

4 结 论
