电机法向力对两种磁浮车辆动力学的影响
2024-01-11李梦雪张敏马卫华罗世辉
李梦雪,张敏,马卫华,罗世辉
电机法向力对两种磁浮车辆动力学的影响
李梦雪,张敏,马卫华*,罗世辉
(西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
中低速磁浮列车采用直线感应电机进行牵引,电机在产生牵引力的同时也会产生法向力,电机法向吸力会对悬浮模块产生垂向激扰,增加悬浮系统的负担。本文利用有限元法对比分析不同气隙下电机牵引力、法向力随速度的变化;建立两种中低速磁浮车辆-轨道耦合动力学模型,分析忽略电机法向力及车体和悬浮架分别在1 kN、3 kN、5 kN冲击力下两种磁浮车辆-轨道耦合系统的垂向动力学响应。结果表明:磁浮车辆在运行速度5 km/h时车辆-轨道耦合共振严重;在法向冲击力小于5 kN时,桥梁动力学响应均符合要求,车体平稳性均为优秀,但当法向冲击力越大时,控制电流越大,因此为减轻悬浮系统负担、提高中低速磁浮车辆-轨道耦合系统的动力学性能,电机法向力应尽可能小。
中低速磁浮;悬浮架;车轨耦合;电机法向力;有限元
中低速磁浮作为一种新型城市轨道交通制式,具有转弯半径小、爬坡能力强、无噪声等优点,符合现代人出行需求,受到专家学者的广泛关注[1-5]。直线感应电机因其结构简单、控制方便、爬坡能力强等优点,常用于中低速磁浮交通实现列车牵引,同时应用电磁铁实现吸力悬浮[6-8]。中低速磁浮列车的牵引依靠直线电机产生的牵引力,但由于直线电机在产生牵引力的同时会产生法向力,因此直线电机还会对磁浮列车动力学性能产生影响[9]。随着中低速磁浮交通在国内外的发展和应用,磁浮车轨耦合振动的问题急需解决[10-11]。为降低中低速磁浮车辆与轨道梁的动力学作用响应,罗世辉[12]发明了一种空簧中置式悬浮架,相比于端置式悬浮架,其具有更好的机械解耦性能[13],但目前直线电机法向力对这两种悬浮架的中低速磁浮车辆-轨道耦合振动动力学响应的影响分析还不够全面。
为研究中低速磁浮车轨耦合振动现象的影响因素,国内外专家学者通过建立越来越细化的磁浮车辆-轨道耦合系统动力学模型,分析不同结构参数、控制系统、悬浮系统参数等对中低速磁浮车辆-轨道耦合系统动力学响应的影响,抑制磁浮车轨耦合振动现象[14-18]。JUN- SEOK LEE等[19]通过研究车辆和导轨的结构参数、运行速度等对低速和中速磁浮车辆动态响应的影响,开发了用于主动控制磁悬浮车辆和柔性导轨结构动态作用分析的数学模型,表明车辆的气隙受车速、路面粗糙度和导轨偏转比的影响很大。胡帛茹[20]分析两种中低速磁浮车辆在混凝土梁上和曲线线路上的动力学响应,指出空簧中置式悬浮架结构有利于减弱车轨耦合共振。张敏等[21]指出中低速磁浮悬浮系统受电机法向力干扰较大,同时通过变滑差频率控制策略降低法向力对中置式中低速磁浮车辆悬浮系统的影响。纪后继等[22-24]研究了电机中置式中速磁浮列车的动力学特性,指出中置电机可提高牵引、制动效率,同时减小轨道不平顺的扰动效果。姚代祯等[25]建立了直线电机车辆系统的机电动力学模型,分析了车辆系统机械及电磁部件的相互作用规律。
为探究电机法向力对两种中低速磁浮车辆-轨道耦合系统动力学性能的影响,本文利用解析法和有限元法对比分析不同气隙下电机牵引力、法向力随速度的变化;建立了两种中低速磁浮车辆-轨道耦合系统动力学模型,分析不同电机法向力激扰对两种磁浮车辆-轨道耦合系统动力学性能的影响。
1 直线电机计算模型
1.1 中低速磁浮直线电机模型
空簧中置式、端置式悬浮架如图1所示。中低速磁浮车辆每个悬浮架包含左、右两个悬浮模块,特殊的模块化结构实现了相对的机械解耦,直线电机、悬浮电磁铁共同安装在悬浮模块上。
直线电机结构如图2所示,通常为单边短定子结构,包含初级和次级。初级安装在悬浮架上随车体一起运动,次级为安装在F轨背面4 mm厚的铝板轨道。直线电机和悬浮电磁铁作用于一个悬浮模块,同时由于直线电机法向力的产生,直线电机和悬浮电磁铁会相互干扰。尤其当法向力表现为吸力时会加重悬浮系统的负担,从而对磁浮车辆-轨道耦合系统动力学性能产生影响。
1.2 直线电机的有限元模型
电机在全速度域包括两个阶段。第一阶段为恒力区,初级电压和电源频率随速度增大而增大,电流不随速度变化,维持在390 A的恒定值;第二阶段为恒功区,电压增大到最大值时保持不变,电源频率继续增大,但电流随速度的增大逐渐减小。相关计算为[13]:


图1 悬浮模块中的直线电机

图2 直线电机结构示意图
利用有限元法在ANSYS/Maxwell仿真软件中对直线电机进行二维磁场仿真分析。由图3(a)可知,初级绕组为双层绕组,共12极116槽,半填充槽前后各9个,基本参数如表1所示。由图3(b)、(c)可知,初级和次级间的磁力线通过气隙闭合,且存在少部分漏磁;出口端磁力线相较于入口端更密集,表明出口端磁感应强度比入口端强,这是直线电机边端效应的一种表现形式。

表1 直线电机参数
1.3 力特性与气隙的关系
电磁气隙是直线电机重要的结构参数,电磁气隙会随着磁浮列车的运行而改变,牵引力和法向力随之改变。根据CJ/T 458-2014[26],中低速磁浮在运行时,悬浮间隙的变化范围为±4 mm,直线电机安装在悬浮模块上,可以认为直线电机气隙变化范围也为±4 mm,则直线电机气隙的变化范围为7~15 mm。

图3 直线电机求解模型及磁力线分布
通过仿真得到不同速度下电机牵引力和法向力随气隙变化的关系,如图4所示。

图4 牵引力和法向力与气隙的关系
电机牵引力和法向力随气隙的增大而减小,第一阶段为恒力区,初级电流保持在390 A,则此阶段电机的牵引力和法向力变化较小;第二阶段包括恒功区,电流逐渐减小,则此阶段电机牵引力和法向力衰减较快,牵引力最大值约4 kN,法向力最大值约5.1 kN。
2 中低速磁浮车轨耦合垂向动力学
2.1 车轨耦合系统动力学模型
本文桥梁模型采用25 m跨距简支梁,利用有限元软件Hypermesh进行网格划分,同时设置相关材料属性,生成.cdb文件导入ANSYS中添加边界条件进行模态分析,自振特性如表2所示。

表2 轨道梁自振频率
建立空簧中置式和空簧端置式两种悬浮架的三悬浮架中低速磁浮车辆模型,主要构件包括车体、空气弹簧、悬浮架、固定滑台、移动滑台、吊杆、横向拉杆、牵引拉杆等,车辆动力学模型的主要参数如表3所示。
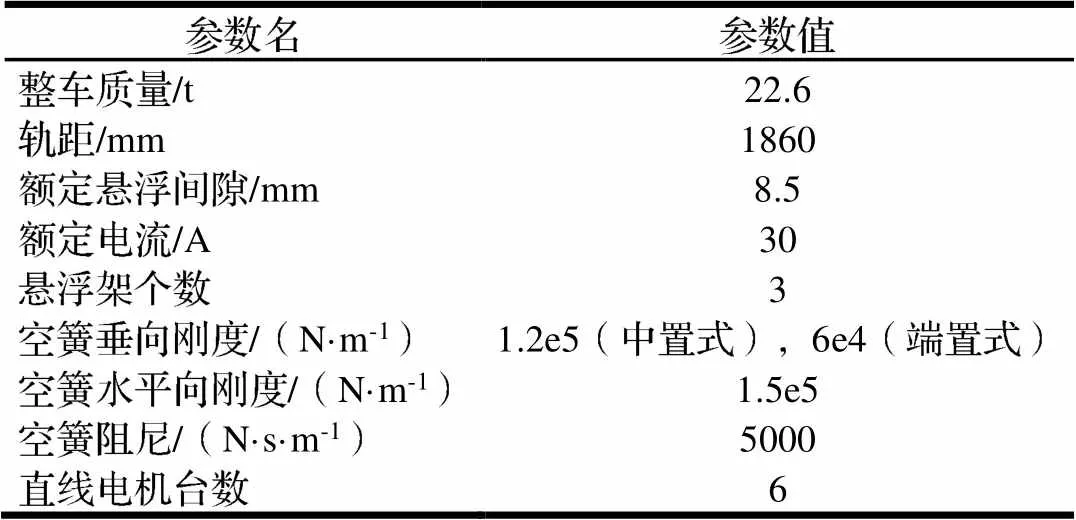
表3 车辆动力学模型主要参数
本文采用UM-ANSYS联合仿真,首先在UM中建立中低速磁浮多刚体模型。在ANSYS中对有限元模型进行模态分析,生成UM可识别的.fss文件,将柔性梁导入UM中,并施加轨道不平顺作为外部激励。空簧中置式悬浮架磁浮车辆-轨道梁耦合系统动力学模型如图5所示。
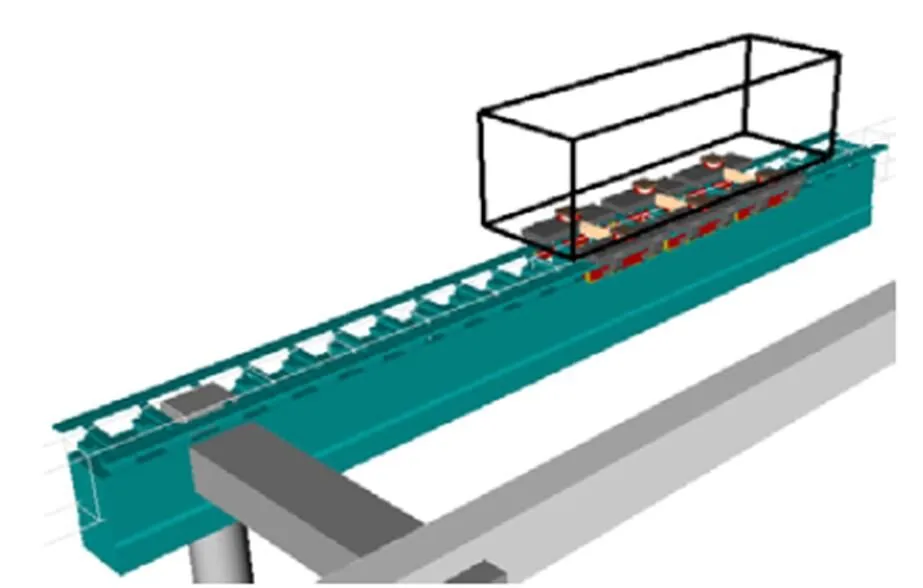
图5 磁浮车辆-轨道梁耦合系统动力学模型
2.2 两种磁浮车辆耦合振动响应分析
2.2.1 桥梁动力学响应
由图6所示,两种磁浮车辆-轨道耦合系统的桥梁跨中垂向动力学响应趋势基本一致,桥梁跨中垂向动位移和垂向加速度总体呈现随速度增大而增大的趋势,两种模型的轨道位移和加速度响应均符合要求,端置式磁浮车辆-轨道耦合系统桥梁的动力学响应略大于中置式磁浮车辆-轨道耦合系统桥梁的动力学响应。

(a)桥梁跨中垂向动位移 (b)图(a)A处放大

(c)桥梁跨中垂向加速度 (d)图(c)A处放大

(e)5 km/h时桥梁跨中垂向加速度振幅 (f)60 km/h时桥梁跨中垂向加速度振幅
图6 桥梁跨中垂向动力学响应及频响
当车辆运行速度为5 km/h和60 km/h时,桥梁跨中动力学响应较大。由图6(e)(f)可知,5 km/h和60 km/h速度时桥梁跨中垂向加速度主频分别为8.89 Hz和8.93 Hz,与桥梁一阶垂弯频率8.92 Hz相近,引起共振。当速度为5 km/h时,速度较小,振动激发更充分,因此速度为5 km/h时桥梁跨中垂向加速度和垂向动位移较大;当速度为60 km/h时,桥梁跨中垂向动位移和垂向加速度小于速度为160 km/h时的桥梁跨中垂向动位移和垂向加速度。
2.2.2 车体动力学响应
由图7可知,两种磁浮车辆的悬浮架垂向加速度、车辆垂向加速度及车体平稳性指标都呈现出随速度增大而增大的趋势,且端置式磁浮车辆的悬浮架垂向加速度、车辆垂向加速度以及车体平稳性均小于中置式磁浮车辆;根据T/CAMET 08003-2018[27]中动力学平稳性要求,两种磁浮车辆的平稳性指标均小于2.5,处于优秀等级。

(a)悬浮架垂向加速度 (b)车体垂向加速度

(c)悬浮模块垂向动位移 (d)车体垂向平稳性指标
图7 悬浮模块及车体动力学响应
3 法向力对两种磁浮车辆耦合动力学的影响
由前述知,电机法向力最大值约为5.1 kN。为探究电机法向力对两种磁浮车辆-轨道耦合系统动力学的影响,引入1 kN、3 kN、5 kN的冲击力。在车辆运行速度为160 km/h时,如图8所示,桥梁跨中垂向动位移和垂向加速度都随冲击力的增大而增大,不同载荷作用下桥梁跨中最大垂向动位移约为1.46 mm,挠跨比小于CJJ/T 262-2017[28]规定的/3800(为桥梁跨度);中置式磁浮车辆-轨道耦合系统桥梁跨中最大垂向加速度约为0.94 m/s2,略高于端置式磁浮车辆桥梁跨中垂向加速度0.90 m/s2,中置式磁浮车辆受法向冲击力的影响略高于端置式磁浮车辆。
由图9、图10、表4可知,悬浮模块垂向加速度、车辆垂向加速度、车辆平稳性指标都随法向力的增大而增大,但总体受电机法向力的影响较小;中置式磁浮车辆的悬浮架垂向加速度、车辆垂向加速度、车辆平稳性指标均大于端置式磁浮车辆。

(a)中置式桥梁垂向动位移 (b)端置式桥梁垂向动位移

(c)中置式桥梁垂向加速度 (d)端置式桥梁垂向加速度
图8 桥梁跨中垂向动力学响应

(a)中置式悬浮架垂向加速度 (b)端置式悬浮架垂向加速度
图9 悬浮模块动力学响应

(a)中置式车体垂向加速度 (b)端置式车体垂向加速度
图10 车体动力学响应

表4 磁浮车辆平稳性指标
注:平稳性指标≤2.5为优秀等级。
当磁浮车辆受到外界激扰时,悬浮控制器通过改变电磁铁线圈中的电流调节悬浮力的大小,使磁浮车辆在额定悬浮间隙附近运行。由图11可知,冲击力越大,悬浮系统就需要越大的控制电流使车辆稳定运行,5 kN冲击力下,中置式磁浮车辆所需的电流约为58 A,端置式磁浮车辆约为56 A,当电流越大时线圈发热越严重,因此为减轻悬浮系统负担,电机法向力应尽可能小。
由前述可知,电机法向力对桥梁动力学响应影响较大,当磁浮车辆低速运行时,车辆发生共振,因此需要探究电机法向力在磁浮车辆5 km/h运行速度时,磁浮车辆-轨道耦合系统的动力学响应。磁浮车辆运行速度为5 km/h时,桥梁的动力学响应如表5所示,可以看出,中置式磁浮车辆跨中垂向动位移和垂向加速度略小于端置式磁浮车辆,挠跨比均小于规范规定的/3800[28]。

(a)中置式 (b)端置式
图11 控制器电流变化曲线
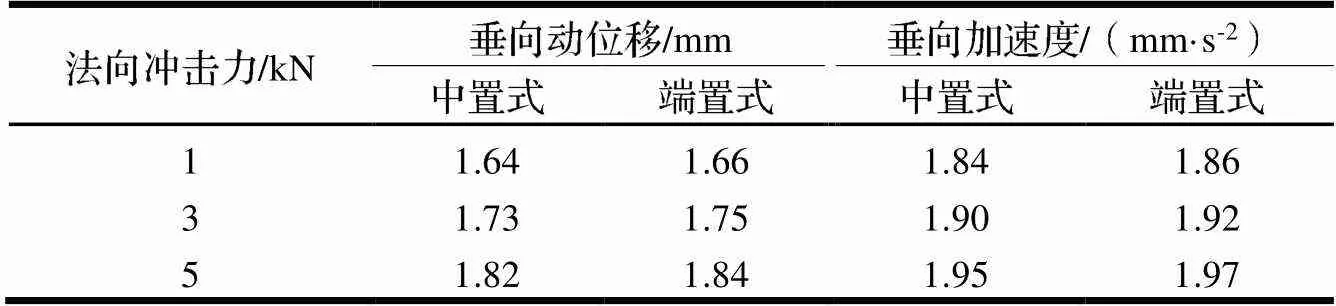
表5 磁浮车辆桥梁跨中垂向动力学响应
4 结语
本文建立直线电机的理论模型和有限元模型,分析不同气隙下电机牵引力和法向力随速度的变化关系;建立两种磁浮车辆-轨道耦合系统,研究法向力对车轨耦合垂向动力学的影响,得到如下结论:
(1)直线电机牵引力和法向力随气隙的减小而增大,总体受气隙变化的影响较小,当速度较高时,电机牵引力和法向力衰减越快。
(2)在运行速度为5 km/h、60 km/h时,磁浮车辆发生共振,忽略法向力冲击时,两种磁浮车辆的桥梁跨中垂向动力学响应随速度的变化趋势基本一致,端置式磁浮车辆-轨道耦合系统的车体动力学响应小于中置式磁浮车辆-轨道耦合系统。
(3)电机法向力表现为斥力时,会加重悬浮系统的负担,冲击越大,悬浮模块、车辆、桥梁跨中垂向动位移和垂向加速度越大,同时所需控制电流越大,因此为降低悬浮系统负担、提高中低速磁浮车辆-轨道耦合系统的动力学性能,电机法向力应尽可能小。
[1]翟婉明,赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报,2016,51(2):209-226.
[2]LEE H W,KIM K C,LEE J. Review of maglev train technologies[J]. IEEE Transactions on Magnetics,2006,42(7):1917-1925.
[3]YAN Lu-guang. Progress of the Maglev Transportation in China[J]. IEEE Transactions on Applied Superconductivity: A Publication of the IEEE Superconductivity Committee,2006,16(2):1138-1141.
[4]马卫华,罗世辉,张敏,等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报,2021,21(1):199-216.
[5]PARK D Y,SHIN B C,HAN H. Korea's urban maglev program[J]. Proceedings of the IEEE,2009,97(11):1886-1891.
[6]范瑜,李文球,杨中平,等. 国外直线电机轮轨交通[M]. 北京:中国科学技术出版社,2010:21-75.
[7]邓仁燕. 中低速磁浮直线感应电机牵引控制系统研究[D]. 成都:西南交通大学,2015.
[8]于加兴. 磁悬浮列车用直线同步电机控制系统的研究[D]. 成都:西南交通大学,2007.
[9]LV GANG,LIU ZHIMING,SUN SHOUGUANG. Analysis of forces in single-side linear induction motor with lateral displacement for linear metro[J]. IET electric power applications,2016,10(1):1-8.
[10]WANG D X,LI X Z,LIANG L,et al. Influence of the track structure on the vertical dynamic interaction analysis of the low-to-medium-speed maglev train-bridge system[J]. Advances in Structural Engineering,2019,22(14):2937-2950.
[11]WANG X H,YANG J W,DU Y P,et al. Risk identification method for high-speed railway track based on track quality index and time-optimal degree[J]. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems,Part A: Civil Engineering,2022,8(2):04022001
[12]罗世辉. 空气弹簧中置的中低速磁悬浮列车走行机构:200710049936.3[P]. 2007-09-05.
[13]张敏. 时速160公里常导磁浮列车直线电机和电磁铁效能提升研究[D]. 成都:西南交通大学,2020.
[14]赵春发,翟婉明,蔡成标. 磁浮列车/高架桥垂向耦合动力学研究[J]. 铁道学报,2001,23 (5):27-33.
[15]李云钢,常文森,龙志强. EMS磁浮列车的轨道共振和悬浮控制系统设计[J]. 国防科技大学学报,1999,21(2):93-96.
[16]时瑾,魏庆朝,吴范玉. 高速磁浮铁路轨道梁振动分析及控制研究[J]. 中国安全科学学报,2003,13(10):76-80.
[17]Yau J D. Vibration control of maglev vehicles traveling over a flexible guideway[J]. Journal of Sound and Vibration,2009,32(1):184-200.
[18]LEE J S,KWON S D,KIM M Y,et al. A parametric study on the dynamics of urban transit maglev vehicle running on flexible guideway bridges[J]. Journal of Sound and Vibration,2009,328(3):301-317.
[19]JUN-SEOK LEE,SOON-DUCK KWON,MOON-YOUNG KIM,et al. A parametric study on the dynamics of urban transit maglev vehicle running on flexible guideway bridges[J]. Journal of Sound and Vibration,2009,328(3):301-317.
[20]胡帛茹. 两种中低速EMS磁浮车辆动力学性能的对比分析[D]. 成都:西南交通大学,2021.
[21]张敏,范屹立,马卫华,等. 滑差频率对磁浮车辆运行性能的影响[J]. 交通运输工程学报,2019,19(5):64-73.
[22]纪后继,刘耀宗,谢新立. 电机中置式中速磁悬浮列车单悬浮架动力学建模及特性研究[J]. 铁道学报,2020,42(9):33-38.
[23]谢新立. 电机中置中速磁浮列车走行机构动力学优化研究[D]. 长沙:国防科学技术大学,2019.
[24]纪后继. 电机中置式中速磁浮列车整车动力学建模分析与测试[D]. 长沙:国防科学技术大学,2018.
[25]姚代祯,闫军,李炳震. 直线电机车辆机电动力学模型的构建与分析[J]. 高技术通讯,2021,31(6):666-670.
[26]中华人民共和国住房和城乡建设部. 中低速磁浮交通车辆悬浮控制系统技术条件:CJ/T 458-2014[S]. 北京:中国标准出版社,2014.
[27]中国城市轨道交通协会. 中低速磁浮交通车辆悬浮架通用技术条件:T/CAMET 08003-2018[S]. 北京:中国铁道出版社,2018.
[28]中华人民共和国住房和城乡建设部. 中低速磁浮交通设计规范:CJJ/T 262-2017[S]. 北京:中国建筑工业出版社,2017.
Influence of Linear Induction Motor Normal Force on Dynamics of Two Types of Maglev Vehicles
LI Mengxue,ZHANG Min,MA Weihua,LUO Shihui
( State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China )
The linear induction motor (LIM) is used for traction of low-to-medium speed maglev train. The LIM will generate normal force while generating traction force, and the normal suction of the LIM will generate vertical excitation to the suspension module, increasing the burden of the suspension system. In this paper, the analytical method and finite element method are used to compare and analyze the changes of traction force and normal force with speed under different air gaps. The vehicle-guideway coupling dynamics models of two types of maglev vehicles at low-to-medium speed are established to analyze the vertical dynamic responses of the vehicle-guideway coupling systems of the two maglev vehicles when ignoring the normal force of the LIM and when the impact force of the vehicle body and levitation frame is 1 kN, 3 kN and 5 kN respectively. The results show that the vehicle-guideway coupling resonance is serious when the speed of the maglev vehicle is 5 km/h. When the normal impact force is less than 5 kN, the bridge dynamic response meets the requirements and the vehicle body stability is excellent. However, the larger the normal impact force is, the larger the control current is. Therefore, in order to reduce the burden of the levitation system and improve the dynamic performance of the low-to-medium speed maglev vehicle-guideway coupling system, the motor normal force should be as small as possible.
low-to-medium speed maglev;levitation frame;vehicle-guideway coupling;linear induction motor normal force;finite element method
U237
A
10.3969/j.issn.1006-0316.2023.12.005
1006-0316 (2023) 12-0025-09
2023-03-01
国家自然科学基金(52102442);中央高校科技创新项目(2682022CX060);中国国家铁路集团有限公司科技研究开发计划(N2021J033);中国铁道科学研究院集团有限公司基金项目(2021YJ026)
李梦雪(1996-),女,河南睢县人,硕士研究生,主要研究方向为磁浮车辆系统动力学,E-mail:2214743409@qq.com。
通讯作者:马卫华(1979-),男,山东滕州人,博士,研究员,主要研究方向为车辆系统动力学,E-mail:mwh@swjtu.edu.cn。
