采用Midas软件的土石坝动力非线性有限元分析

孙海瑞

（新疆云沣水利设计咨询有限公司，乌鲁木齐 830002）

水库大坝在强震作用下易遭受破坏， 尤其是松散土石坝，在地震作用下易出现陷落、坍塌等现象，结构稳定和安全运行受到威胁， 因此开展土石坝地震动力响应分析具有重要的现实意义［1］。本文基于土石料等价线性黏弹性模型和动力平衡计算公式［2］，建立有限元模型， 并以乌斯通沟水库沥青混凝土心墙砂砾石坝为例，进行动力分析计算，旨在为土石坝的设计、施工及运行安全提供依据。

1 工程概况

乌斯通沟水库是一座具有综合效益的水库枢纽工程，主要任务是灌溉和工业供水，遏制灌区地下水超采，水库总库容1440 万m2，工程等别为Ⅲ等，工程规模为中型。

大坝为沥青混凝土心墙砂砾石坝， 最大坝高为73.0 m ，为2 级建筑物。坝顶长度为261.90 m，大坝坝顶宽9.0 m，上游坝坡1∶2.25、1∶2.2，上游坝坡采用250 mm 厚的现浇混凝土板护坡； 下游坝坡1∶2.0、1∶1.8，下游坝坡采用300 mm 厚的干砌石+混凝土网格梁护坡。坝体防渗采用沥青混凝土心墙，左、右岸坝下基岩采用帷幕灌浆防渗；河床段采用混凝土防渗墙+帷幕灌浆防渗；左坝头防渗线延长段长度47.0 m，右坝头防渗线延长段长度49.1 m，大坝防渗线总长363.0 m。

工程区地震动峰值加速度为0.22 g，地震动反应谱特征周期为0.40 s， 对应的地震基本烈度为Ⅷ度，所以，本工程地震设防烈度按Ⅷ度设防，大坝采用乙类抗震设防。

本文按照规范的标准和方法， 利用Midas 有限元分析软件，对该大坝进行动力计算，计算地震工况下的坝体动力反应及地震永久变形， 验证结构设计的合理性和工程的安全可靠性。

2 计算参数及方法

2.1 计算参数

2.1.1 静力参数

动力计算是在静力计算分析的基础上进行，初始静应力对土石坝地震荷载作用下的动力反应存在较大影响，静力分析时，坝体坝基材料采用邓肯等人提出的非线性弹性的双曲线E～V 模型。

该土石坝材料静力计算参数如表1［3］。

2.1.2 动力参数

El Infiernillo、Takimi、碧口、紫坪铺等已建大坝遭受的实际地震灾害表明： 现代重型振动碾压土石坝在地震过程中主要表现为振缩特性， 这一方面使大坝震后更为密实，抵御地震破坏的能力得到加强，同时密实的坝体地震反应更为剧烈， 大坝特别是坝顶的加速度反应更大，鞭梢效应更强，大坝局部抗震设计措施必须得到加强。

坝体动力反应计算采用国内外广泛使用的等价线性黏弹性模型， 地震永久变形采用等价节点力法进行计算。

根据地勘试验资料， 该土石坝动力分析计算的各项参数如表2。

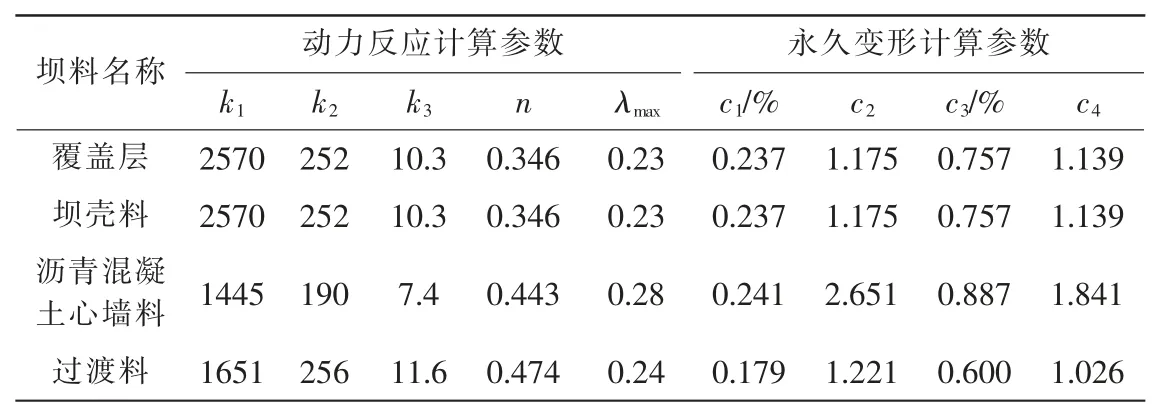
表2 动力计算参数

2.2 计算公式

2.2.1 动力平衡计算公式

由相关研究成果，动水压力对建于基岩上的100 m级土石坝影响较小［4］，本文忽略动水压力的影响，动力平衡计算公式如下：

其中：

故

式中 [M ]为整体质量矩阵； [K ]为整体劲度矩阵；[C ]为整体阻尼矩阵； {δ¨g}为地震加速度列阵； {δ¨}为相对加速度列阵； {δ˙}为相对速度列阵；{δ }为相对位移列阵；[G ]为地震加速度3 个分量到n 个自由度体系的n 维空间的转换矩阵。

动力计算采用Wilson-θ 法， 将整个地震运动过程按每时段1～2 s 划分成多个时段，进行时程逐步数值积分， 求解动力平衡方程式。迭代精度控制条件要求为：

式中 Gi和λi分别为单元第i 次迭代计算时的动剪模量和阻尼比；ε 值在10%左右。

2.2.2 坝体震后永久变形计算公式

粗粒料的动力性质研究成果比较丰富， 一般采用振动硬化模型， 该模型可反映粗粒料振动硬化对大坝抗震的不利影响［5］。

通过动力非线性有限元分析计算坝体各单元在地震过程中的残余应变，计算公式如下：

式中Δεγp为残余剪切应变；Δενp为残余体积应变；Pa为大气压力，为平均有效主应力；k1，k2，k3，nGM，n1为试验参数。

依据Prandtl-Reuss 流动法则，根据式（8）将残余应变换算成直角坐标系下的应变：

式中p 为平均主应力，q 为广义剪应力。

计算出直角坐标下的残余应变增量后， 可得等效结点力为：

式中 [B ]为应变转换矩阵；[D ]为弹性矩阵； {Δ εp}为直角坐标系下的残余应变增量。

将所求的等效结点力加载于大坝结构， 再按照静力非线性有限元计算， 得到的坝体变形结果就是动力计算的地震永久变形。

3 有限元模型

3.1 坝体有限元计算网络剖分

本次计算采用Midas 软件， 以河床典型剖面为基准， 沿坝轴线方向将大坝分为43 个计算剖面，计算坐标系X 轴为河道下游指向上游，Y 轴为垂直地面方向以向上为正，向下为负；坝轴线方向设为Z 轴方向，以向右岸为正，向左岸为负。

整个计算模型共划分得到总结点数10792 个，总单元数10367个， 其中包括75个防渗墙单元和728 个心墙单元，网格划分图如图1［6］。

图1 大坝剖分网格立视图

3.2 坝体填筑及蓄水加载过程模拟

根据拟定施工顺序和大坝结构单元划分情况，将整个大坝施工（包含地基覆盖层）和蓄水过程共分为23 级荷载进行加载，由此动态模拟大坝的填筑过程及蓄水过程，为了较好地模拟加载，每一级荷载级均采用一次性加载方式， 动力计算工况为设计规范波地震，计算水位为正常蓄水位905.00 m 高程。

4 坝体动力非线性有限元计算成果分析

4.1 坝址基岩地震动输入

土石坝抗震计算分析中， 基岩地震动输入规范反应谱地震波（以下简称规范波）地震动加速度时程曲线进行大坝动力计算［4］。

查阅《中国地震动参数区划图》，可确定乌斯通沟工程场地特征周期Tg=0.40 s，根据《水电工程水工建筑物抗震设计规范》，标准设计反应谱平台最大值βmax=1.60，最小值βmin=0.478，大于βmax的20%，满足规范要求。查阅《中国地震动参数区划图》,可确定乌斯通沟地震峰值加速度为0.20 g，因此本文计算过程中以0.20 g 的地震峰值加速度作为设计规范波地震。

动力分析需确定该地区的地震加速度时程曲线,采用SIMQKE_GR 程序生成规范谱地震波，水平向（顺河向和坝轴向）地震动加速度时程曲线的生成结果如图2。 其中设计地震规范波水平向地震动峰值加速度为2.0 m/s2，竖向地震动加速度取水平向地震动加速度的2/3，峰值加速度为1.33 m/s2。

图2 规范谱地震波合成（水平向）

4.2 计算成果与分析

4.2.1 坝体绝对加速度反应

大坝在设计地震规范波作用下顺河向的绝对加速度反应极值分布如图3（a）。由图可知，在河床0+137 坝段附近的坝顶部位出现顺河向地震加速度反应极值，放大倍数为2.61 倍，最大反应为522 gal。

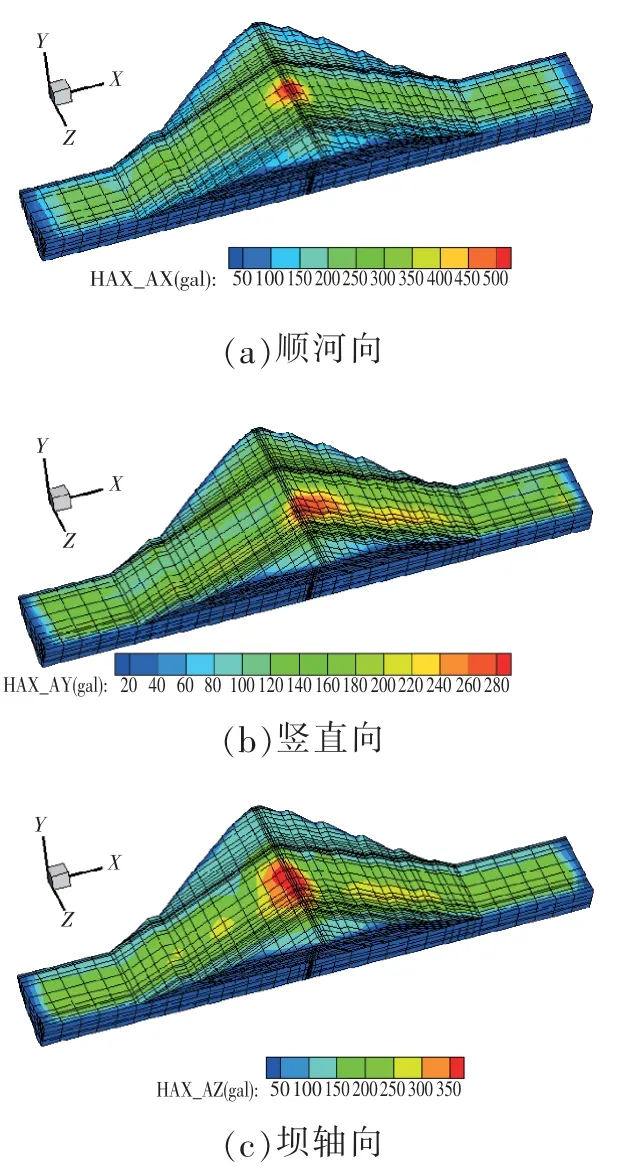
图3 设计地震规范波作用下坝体加速度反应极值分布 单位：gal

大坝在设计地震规范波作用下竖直向的绝对加速度反应极值分布如图3（b），竖直向地震加速度反应极值出现在河床0+159 坝段附近的坝顶部位，放大倍数为1.47 倍，最大反应为293 gal。

大坝在设计地震规范波作用下坝轴向的绝对加速度反应极值分布如图3（c），同顺河向类似，在河床0+137 坝段附近的坝顶部位出现坝轴向地震加速度反应极值，放大倍数为1.94 倍，最大反应为387 gal。

由图3 可知， 大坝3 个方向的加速度反应极值最大值均发生在坝顶部位，且几乎保持对称分布，符合实际规律。

4.2.2 坝体最大振幅

大坝在设计地震规范波作用下坝体的最大振幅分布如图4，图中数据为3 个方向的合位移。由图4 可知，坝体最大振幅出现在坝顶，最大达5.4 cm。

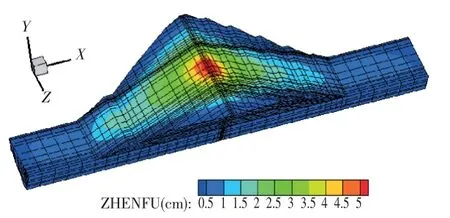
图4 设计地震规范波作用下坝体最大振幅 单位：cm

4.2.3 动剪应力极值

大坝在设计地震规范波作用下坝体最大横剖面的动剪应力极值分布如图5。Txy方向的动剪应力在坝体心墙与反滤料相接区约850.00 m 高程出现较大值， 最大动剪应力为144 kPa； 在心墙与反滤料相接区域，Txz方向的动剪应力较大， 最大动剪应力为122 kPa；Tyz方向的动剪应力极值主要存在于心墙与基座相接部位，最大动剪应力为75 kPa。

图5 设计地震规范波作用下坝体动剪应力极值分布 单位：kPa

4.2.4 地震永久变形

大坝在设计地震规范波作用下坝体的顺河向、竖直向和坝轴向的永久变形分布如图6。 由图6 可知，坝体顺河向的永久变形基本指向下游，最大值为4.3 cm，出现在0+137 剖面；竖直向永久变形最大值为12.4 cm， 位于0+137 剖面的坝顶；坝轴向永久变形为两岸向河谷内发展，基本成对称趋势分布，最大值左岸指向右岸为3.5 cm，右岸指向左岸为3.5 cm。

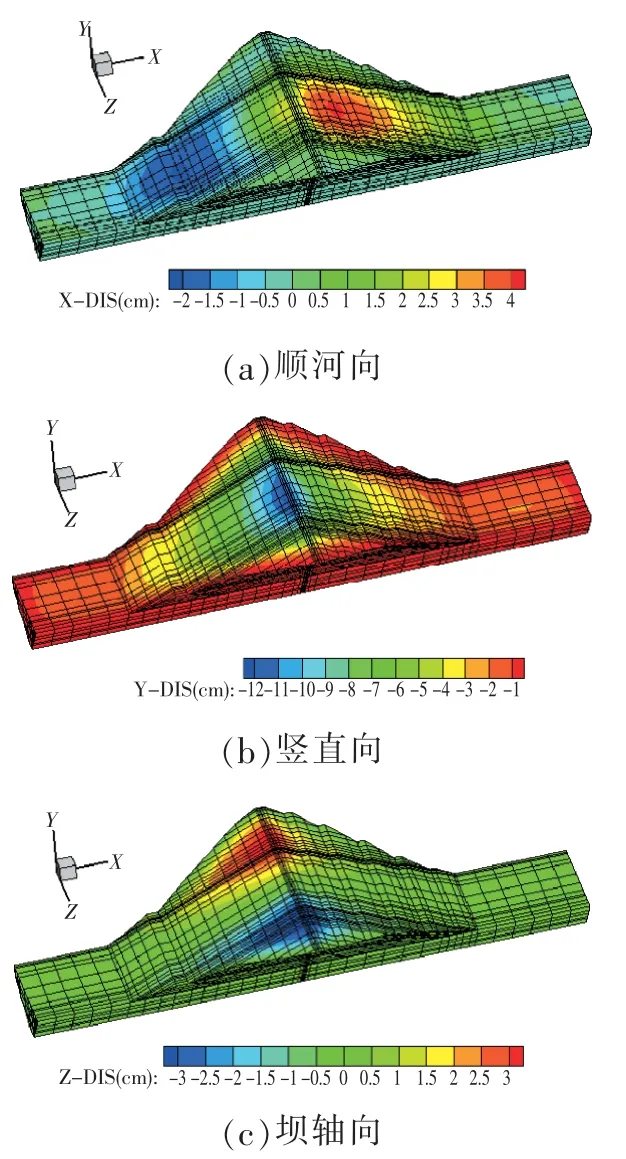
图6 设计地震规范波作用下坝体震后永久变形 单位：cm

5 结语

（1）大坝在设计地震规范波作用下3 个方向的绝对加速度反应极值基本出现在坝顶部位，最大加速度反应的放大倍数约2.6 倍，存在“鞭梢效应”。

（2）坝体动剪应力峰值主要分布在心墙与反滤料相接的两侧区域，最大值为144 kPa；坝体最大振幅出现在坝顶，最大达5.4 cm。

（3）计算竖直方向地震永久变形最大值为12.4cm，位于0+137 剖面的坝顶偏上游区域。

（4）综上所述，最大加速度反应、最大永久变形都位于坝顶，其分布规律合理，乌斯通沟沥青混凝土心墙坝设计方案合理，采取一定抗震措施后，能满足抗震要求。