改进RRT 算法的四旋翼无人机路径规划方法

冯迎宾，赵子君，晏佳华

(沈阳理工大学自动化与电气工程学院，沈阳 110159)

由于四旋翼无人机具有灵活轻便、机动性好、动力强等特点，被广泛应用在多个领域。 当无人机在执行灾害救援、军事侦察等实际应用任务时，飞行路径上可能存在多种障碍物，为保证无人机安全，四旋翼无人机应具备自主避障能力。 实时的路径规划是四旋翼无人机实现自主避障的关键技术，其目的是在一定范围内规划出一条从起点到终点避开障碍物并适合无人机飞行的路径。

目前，学者提出的路径规划方法主要分为两类:基于采样的路径规划和基于搜索的路径规划[1]。 快速扩展随机树(rapidly-exploring random tree，RRT)[2]算法为基于采样的路径规划方法的代表性算法之一，已经被广泛应用于工程实践中，例如机械臂运动规划[3]、机器人路径规划[4-6]以及无人机航迹规划[7-9]。 RRT 算法无需对空间进行预处理即可进行随机采样，通过对采样点进行处理，最终得到一条无碰撞的路径。 RRT 算法具有概率完备性、搜索范围广等优点，但其生成的路径并不是最优的。 针对这一问题，文献[10]提出了RRT*算法，通过对扩展节点周边一定范围内的节点进行选择，找到合适的父节点，从而规划出渐进最优的路径。 文献[11]提出了RRT-connect方法，在起始点和终点同时生成两棵扩展随机树进行路径的寻找，加快了路径寻找速度。 文献[12]在RRT 扩展过程中通过调节采样区范围提高算法效率。

由此可见，改进的RRT 算法主要是对搜索策略和采样区域选择进行优化。 本文提出一种从预生成路径本身出发，通过构建重规划起止点进行RRT 规划的方法。 在RRT 算法中通过缩小采样区域，从而减少采样次数，并且引入目标偏向寻优策略，使得采样点具有向目标点偏转的概率。 在平滑度优化策略中，去除冗余初始航迹点的同时与四旋翼无人机性能约束相结合，利用B 样条曲线对航迹点处理，从而获得更加符合四旋翼无人机特性的可行路径。

1 基本RRT 算法

在路径规划过程中，将四旋翼无人机视为质点，RRT 算法从起始点出发，在空间中随机生成采样点，当采样到目标点或其附近区域时停止，即生成一颗同时包含起始点和目标点的随机树，在树中可以找到一条从起始点出发由树的节点构成最终到达目标点的路径。

路径搜索过程如图1 所示，图中Kstart表示起始点，Kgoal表示目标点，正方形和圆形表示障碍物。 起始点Kstart可作为随机树的根节点，RRT 算法首先在非障碍物区域内随机生成一个采样点Krand作为目标点，在找到距离Krand最近的树扩展节点Knear，以Knear为基准点在其与Krand的连线上朝着Krand方向按照预定步长S生成新的节点Knew，如果在预定步长内与障碍物发生碰撞则放弃Knew再重新生成Krand，如果在预定步长内无障碍物碰撞则保留Knew。 重复上述步骤，经过多次迭代，当Knew在目标点Kgoal附近区域时则完成随机树的构建，即找到了一条由起始点抵达目标点的可行路径。

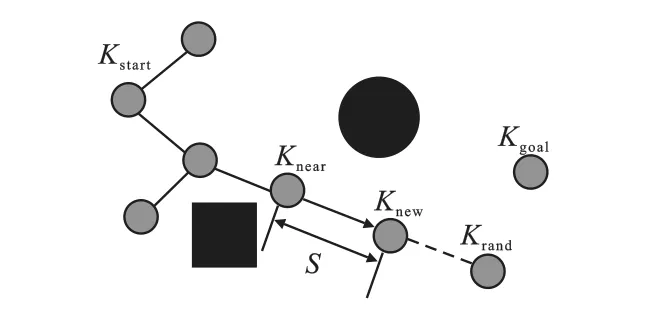
图1 路径搜索过程Fig.1 The path search process

2 改进RRT 算法的路径搜寻方法

2.1 配置空间等效问题

四旋翼无人机在飞行过程中可能存在不同类型的障碍物，例如电线杆、树木、指示牌等，但障碍物的细节对无人机的路径规划意义不大，因此在配置空间中需要对不同类型的障碍物进行统一等效处理。

假设对于任何障碍物，均可找到一个质量分布均匀的长方体将其完整包围[13]。 本文对于空中障碍物将其等效为圆球，假设圆球的圆心为长方体质心，圆球半径Rq由公式(1)求得。 对于地面障碍物，本文将其等效为圆柱，假设圆柱体底面圆心为长方体底面中心点，底面半径Rc和圆柱高度Zc由公式(2)求得。 图2 为本文障碍物等效示意图。

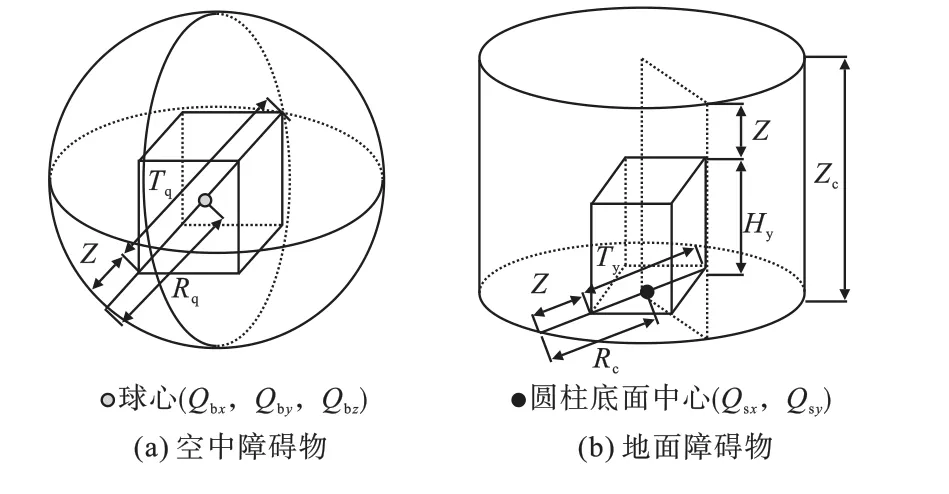
图2 障碍物等效示意图Fig.2 Equivalent schematic diagram of obstacles

式中:Z为四旋翼无人机轴距；Tq为长方体对角线长度；Ty为长方体底面对角线长度；Hy为长方体的高。

2.2 四旋翼无人机性能约束

在空中飞行的四旋翼无人机不仅受到环境因素影响，还需考虑其自身性能约束，避免无人机发生剧烈运动，导致失控。 因此，在路径规划时需综合考虑航迹距离、偏航角和俯仰角等性能约束条件。

2.2.1 最远航迹约束条件

四旋翼无人机在飞行过程中由于受到自身动力限制并不能无限制距离飞行，因此在轨迹规划时应该加入航迹约束。 无人机最远飞行航迹由无人机搭载的电源和通信能力决定，路径重规划得出的轨迹由n个航迹点组成，其轨迹长度总和应小于最远飞行航迹距离。 航迹约束条件可表示为

式中:i＝2，3，…，n；Dis(ki-1，ki)为相邻航迹点之间的欧几里得距离；Smax为无人机最远飞行航迹距离。

2.2.2 最短航迹约束条件

四旋翼无人机在飞行时要尽量以匀速状态保持直线飞行或者以恒定的航向角完成转弯动作，频繁的姿态调整对无人机控制系统有着较高的要求，电机需要不断调整旋转速度，会造成动力源消耗过多。 因此需要进行最短航迹约束，即路径重规划的过程中期望每个航迹点之间的距离大于预设的最短航迹距离Smin，如果产生n个航迹点，则最短航迹约束可以表示为

2.2.3 最大偏航角约束

偏航角为无人机实际航向与计划航向之间的夹角，如果在飞行过程中偏航角过大可能会造成无人机远离预设航向，导致飞行任务失败，甚至失控，因此，需要在路径规划过程中设定最大偏航角限制。 在配置空间中，假设生成n个航迹点，对于除第n点外的其他航迹点ki(i＝2，3，…，n-1)为原点建立三维坐标系，在此坐标系中标定下一个航迹点ki+1的位置，这两个航迹点之间的连线在xkiy平面的投影线段与x轴之间的夹角ρ应比设定的四旋翼无人机最大偏航角ρmax小，如图3 所示，ki与ki+1为相邻航迹点，最大偏航角约束可表示为

图3 偏航角示意图Fig.3 Schematic diagram of yaw angle

式中x、y为航迹点坐标值。

2.2.4 最大俯仰角约束

俯仰角为无人机机头方向的机体轴与水平面之间的夹角，俯仰角过大会极大降低飞行过程中的稳定性，甚至造成无人机失控，因此需要设定最大俯仰角对其进行约束。 最大俯仰角限制与最大偏航角类似，如图4 所示，在xkiz平面的投影线段与x轴之间的夹角γ应比设定的四旋翼无人机最大俯仰角γmax小，最大俯仰角约束可表示为

图4 俯仰角示意图Fig.4 Schematic diagram of pitch angle

式中x、z为航迹点坐标值。

2.3 路径重规划策略

2.3.1 构建重规划起止点

在配置空间中，设置起始点为Ka(xa，ya，za)，目标点为Kb(xb，yb，zb)，先从xa指向xb预生成一条忽略障碍物的直线路径，然后对于这条直线进行离散化处理，生成一组相邻数组为单位步长的三列矩阵。 在路径规划过程生成的点属于直角坐标系，为了确定配置空间中点、线之间的关系以及各种夹角的角度，这时需要将其转换为球坐标系。 已知直角坐标系下Ka和Kb的坐标点，需要根据公式(7)将其转换为球坐标系，坐标系示意图如图5 所示，图中以Ka为原点建立三维坐标系，并在坐标系中标定Kb的位置，本文中其他需要进行坐标系转换的坐标点均按此方法建立坐标系。

图5 坐标系示意图Fig.5 Schematic diagram of coordinate system

式中:l为Ka(xa，ya，za)和Kb(xb，yb，zb)之间的欧几里得距离；θ为Ka和Kb的连线与z轴夹角；ρ为Ka和Kb的连线与x轴夹角。

式中:i＝1，2，3，…，k；x1、y1、z1为需要离散化处理线段的起始点坐标值。

依次对矩阵Γ每一行按照公式(9)计算欧几里得距离进行检测以判断是否在障碍物内，并将包含在障碍物内的元素存入3 列矩阵Λ。

式中:j＝1，2，3，…，k；Γj1，Γj2，Γj3分别为矩阵Γ每行的元素。

以矩阵Λ中间行数元素λmid为起点，平行于配置空间中的底面，做的垂线γ，并对γ根据公式(8)以单位步长进行离散化，根据公式(9)找到包含在障碍物内的元素，分别找到最贴近障碍物两侧边界的元素Qr与。 根据公式(10)计算与矩阵Λ中间维数元素Λmid的欧几里得距离，比较两者长度，将距离近的边界元素保存为Q。 以Λmid为起点，以Q为方向，在γ离散化后得到的点中找到远离障碍物并在10 ～30 倍单位步长中的一个元素保存为Qmid。

矩阵Λ的首尾元素也存在于矩阵Γ，矩阵Γ相邻元素距离为单位步长，以矩阵Λ首尾元素为起点向矩阵Γ首行和尾行两个方向进行扩展，找到远离障碍物并在20 到30 倍单位步长之间的两个元素，距离起始点Ka近的元素保存为重规划起点Qstart，另一个元素保存为重规划终止点Qgoal，如图6 所示。

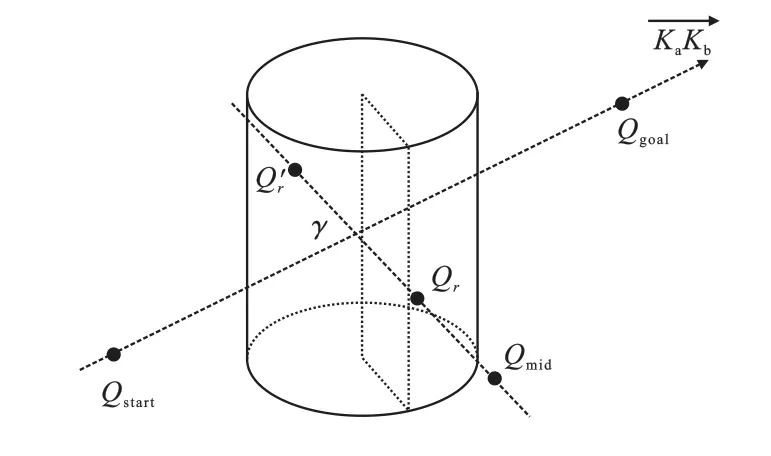
图6 重规划示意图Fig.6 Schematic diagram of reconstruction

使用RRT 算法进行路径搜索，首先搜索Qstart到Qmid路径，再搜索Qmid到Qgoal的路径。

2.3.2 RRT 算法采样点选取改进

在配置空间中，基本RRT 算法寻找Ka和Kb之间路径时由于采样区域过大，从而造成采样次数过多使得随机扩展树分支多。 本文在路径重规划过程中，通过重新选取RRT 算法起止点，改进采样区域选择范围，降低采样次数，从而减少随机树的分支数量。

本文在采样时引入基于概率的目标偏向寻优策略[14]，如公式(11)所示，设置一个小于1 的目标偏置阈值Pth。P为在0 ～1 范围由均匀分布获得的一个概率值，当P＜Pth时，设置目标点为随机点，这样使得随机树具有向目标点Kgoal方向扩展的可能，当P＞Pth时，则使用sample()函数生成采样点。

基本RRT 算法采样时区域范围为Ka和Kb为顶点构成的三维空间，本文中将采样区域缩小为Qstart和Qgoal为顶点构成的三维空间，如图7 所示。 新的采样区域范围由公式(12)计算得出。

图7 采样区域范围Fig.7 Sampling area range

式中:xstart、ystart、zstart为Qstart的三维坐标；xgoal、ygoal、zgoal为Qgoal的三维坐标；s'x、s'y、s'z为x、y、z三轴上的长度。

sample()函数生成的采样点(xstart、ystart、zstart)为Qstart，由公式(13)计算得出。

2.4 平滑度优化策略

由于RRT 算法随机性强从而导致路径重规划后得到的初始轨迹通常不平滑、存在过多的转折。 这些轨迹由初始航迹点连接得到，为了提高路径平滑度，满足四旋翼无人机实际飞行需求，需要对初始航迹点进行筛选从而得出合适的航迹点，然后利用B 样条对其进行平滑处理。 平滑度优化策略总流程如图8 所示。

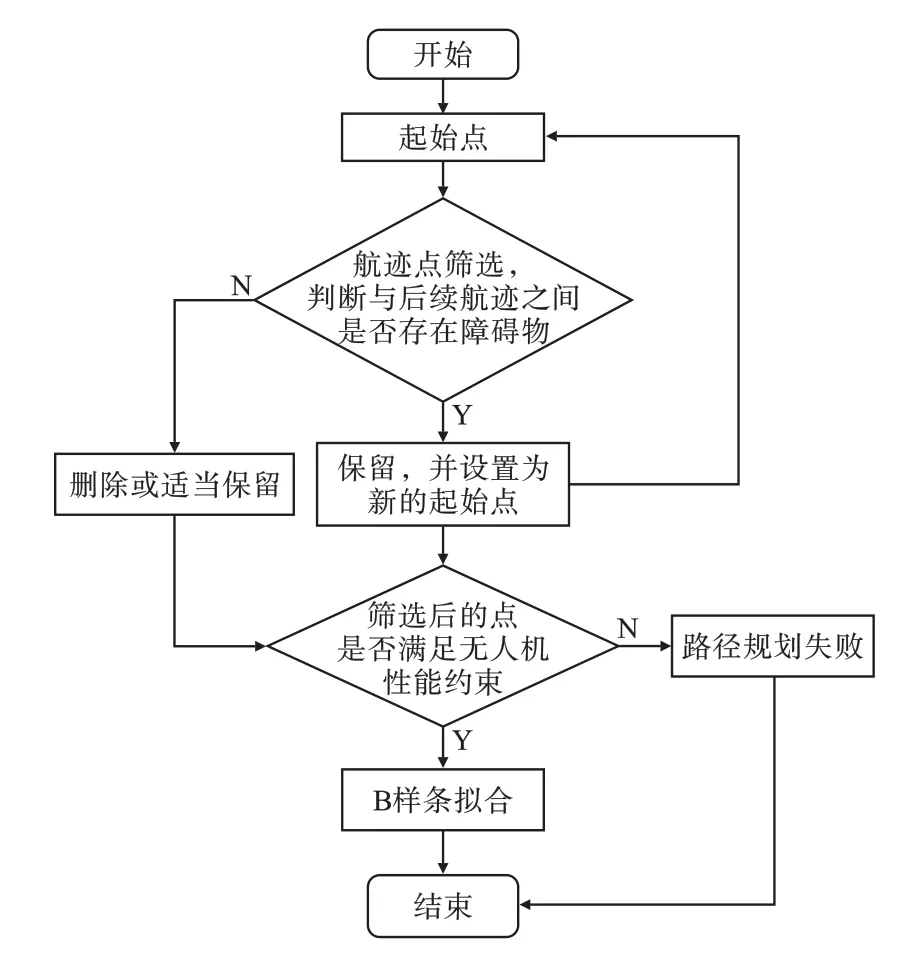
图8 平滑度优化策略流程Fig.8 Smoothness optimization strategy process

航迹点筛选是将第一个初始航迹点设置为起始点，依次检测后续航迹点与起始点连线之间是否有障碍物，如果连线不经过障碍物则将其视为冗余点删除并检测下一个航迹点，如果有障碍物则为被保留航迹点并将其设置为新的起始点，再重复上述操作，直至检测到最后一个初始航迹点。 为了便于B 样条进行优化，使得路径更具有可行性，会适当保留个别冗余点，保留原则为对被保留航迹点之前第四个至第九个冗余点中随机抽取一个，如果被保留航迹点之前冗余点数量不足四个则不保留。 在得到航迹点后对航迹点进行安全性检测，即判断航迹点是否满足四旋翼无人机性能约束。

B 样条是贝塞尔曲线一般化形式之一，具有保凸性、凸包性以及几何不变性等多种优良特性[15]，常用于对于轨迹进行平滑处理[16]。 本文将剔除冗余点后的航迹点作为B 样条控制点，从而生成平滑的轨迹。

3 数字仿真分析

为验证上述算法的有效性，本文基于Matlab 2020a 编程，在中央处理器为Intel(R)Core(TM)i5 -8300H CPU ＠ 2. 30 GHz、显卡为NVIDIA GeForce GTX 1050 Ti 的计算机上进行数字仿真实验。

为了验证本文算法的性能，与RRT 算法进行了对比仿真实验，且选取的概率目标偏向巡游策略相同。 在仿真实验过程中，仿真环境设置为1 000 ×1 000 ×300 区域，设置起始点Ka(0，0，0)、目标点Kb(900，900，200)，设置6 个经过等效后的障碍物，其相关信息如表1 所示，实验环境如图9 所示。 RRT 算法未添加无人机约束，本文算法最短航迹约束条件设置为Smin＝1(无量纲)，将最大偏航角以及最大俯仰角设置为60°，即ρmax＝γmax＝tan 60° ＝1.732。

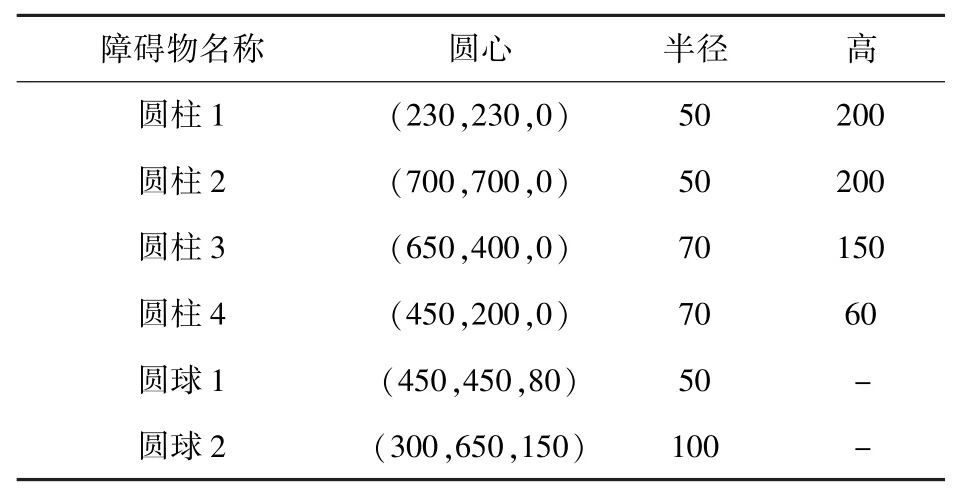
表1 等效障碍物信息Table 1 Parameters of equivalent obstacles

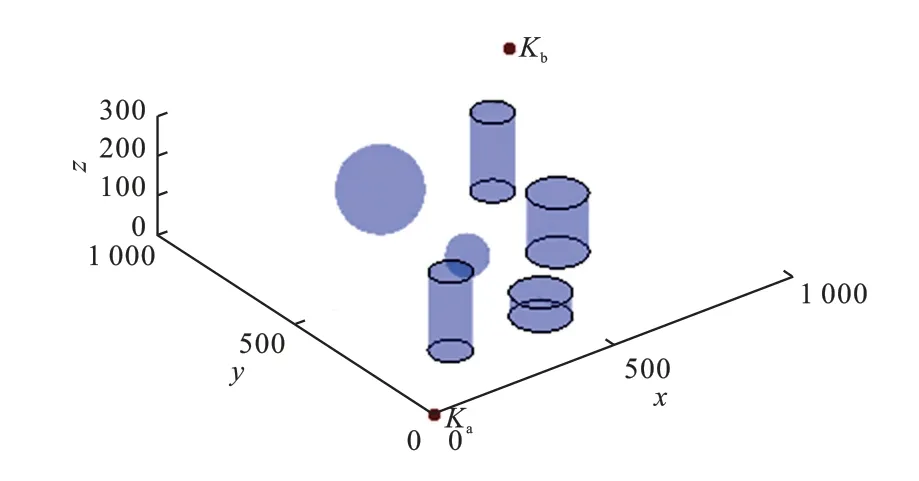
图9 仿真环境Fig.9 Simulation environment

RRT 算法实验结果如图10 所示，本文算法实验结果如图11 所示，图12 表示本文算法的部分重规划结果。 由图10 ～12 可知，重规划过程中改进RRT 算法的随机树的分支相对于RRT 算法显著减少，经过平滑度优化策略处理过的轨迹中的航迹点冗余点更少，相对于重规划RRT 算法生成的原轨迹更加顺滑，轨迹转弯次数更少，更加符合四旋翼无人机的实际飞行需求。

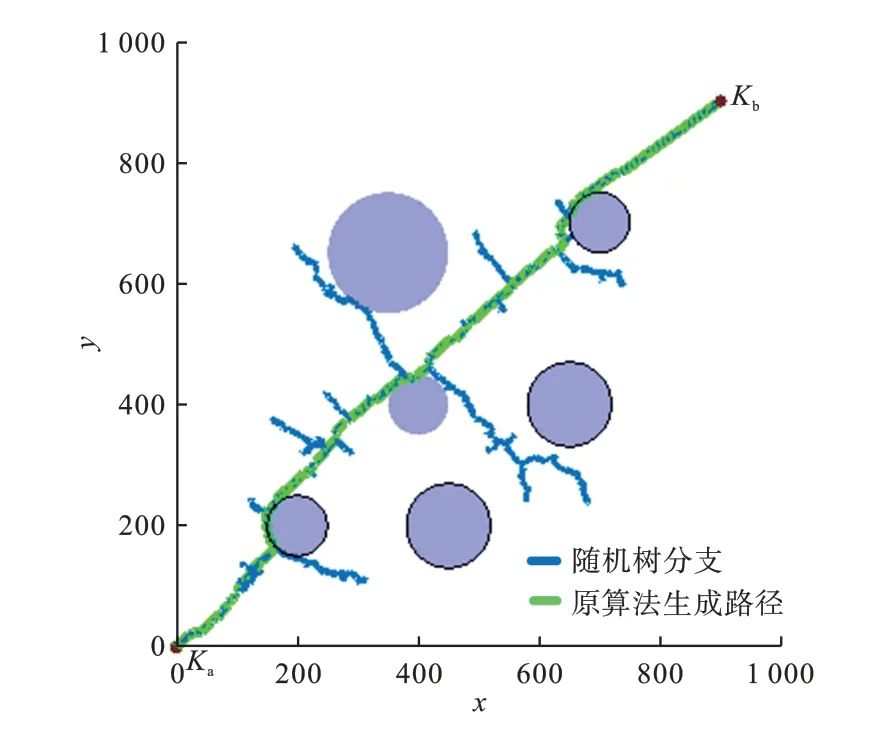
图10 RRT 算法xy 平面视图Fig.10 xy-plane view of RRT algorithm

图11 本文算法xy 平面视图Fig.11 xy-plane view of algorithm in this paper

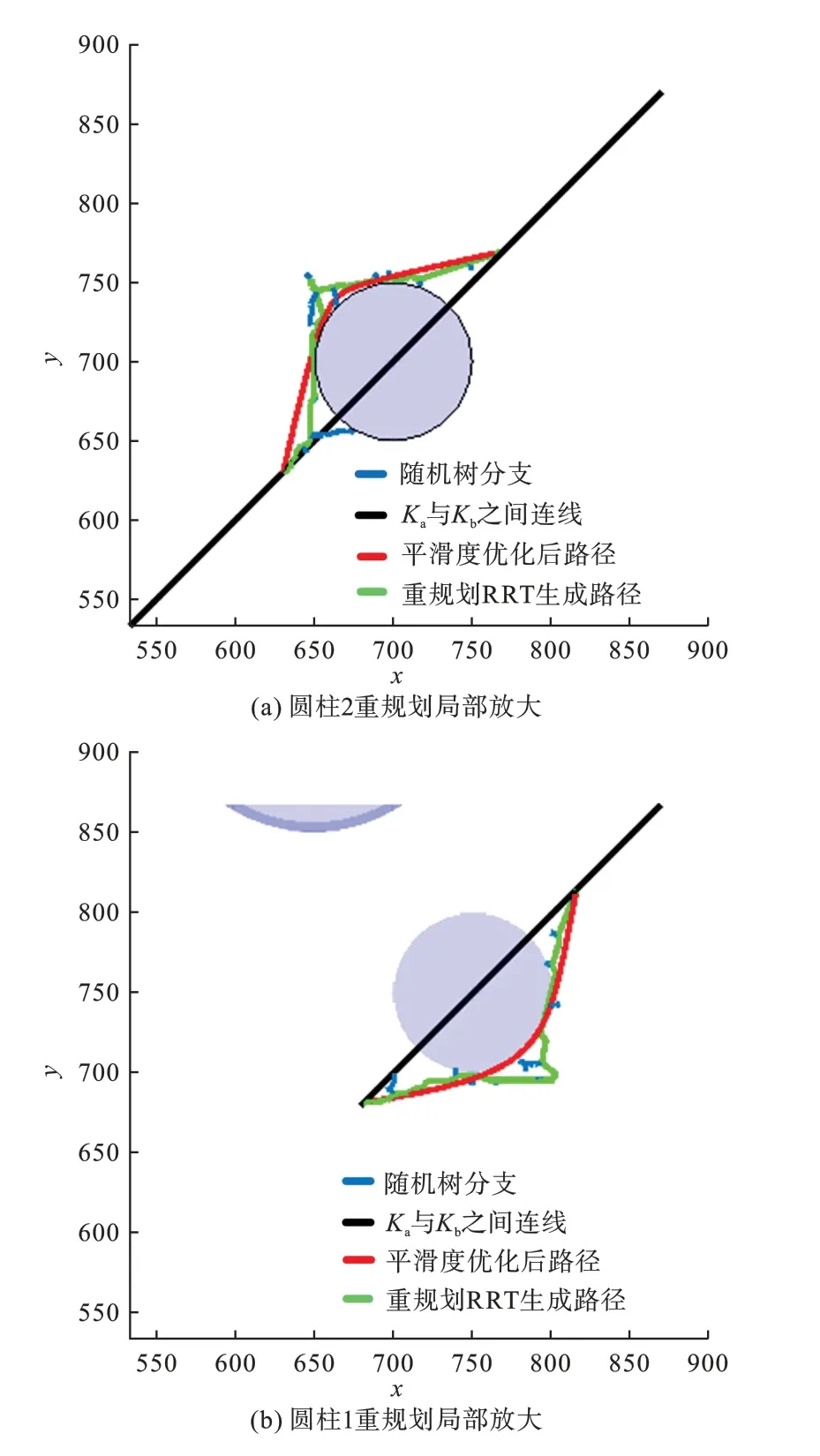
图12 本文算法重规划xy 平面视图Fig.12 The reprogrammed xy-plane views of algorithm in this paper

为验证本文提出算法的鲁棒性，实验分为2组进行，每组运行RRT 算法和本文算法各20 次，分别统计平均采样次数、程序平均运行时间和Ka至Kb平均航迹距离数据，结果如表2 所示。

表2 实验结果对比Table 2 Comparison of experimental results

实验结果表明:本文算法相对于RRT 算法程序有效降低了采样次数，平均采样次数仅为RRT算法的24.60%；平均运行时间更少仅为原算法的29.05%。 表2 中航迹距离为欧几里得距离，可以看出本文算法从起始点Ka到目标点Kb的航迹距离比RRT 算法的结果有所减少，为RRT 算法的94.60%。

4 结论

本文提出了一种改进RRT 算法的四旋翼无人机路径规划方法，旨在解决RRT 算法随机性强、采样次数过多以及生成轨迹曲折的问题。 在配置空间中对障碍物进行等效处理，忽略障碍物细节，降低了算法运行环境的复杂度。 在路径重规划过程中，通过重新构建采样区域范围，有效降低了RRT 算法的采样次数，引入基于概率的目标偏向寻优策略，使采样点以一定概率向重规划目标点方向进行扩展。 在平滑度优化策略中，选择性去除初始航迹中的冗余点并兼顾无人机性能约束，通过B 样条曲线产生平滑路径，使得生成的路径更加贴合无人机实际需求。