基于改进变分模态分解的抽油井偏磨程度诊断

李翔宇，邬亦晗，袁春华

(沈阳理工大学自动化与电气工程学院，沈阳 110159)

目前，我国大多数油田处于开发的中后期[1]，绝大多数自喷式油井已改造为机械采油井，某些新开发油井甚至直接采用机采方式进行开采[2]。机采时抽油机带动抽油杆做往复运动，其持续运行易导致杆管出现偏磨现象，主要原因有:

1)地层运动导致套管产生变形，变形的套管对油管产生挤压作用，改变油管的方向和位置，油管偏移造成抽油杆和油管在局部产生偏磨[3]；

2)当抽油杆整体向下运动进行冲程时，中和点以下的抽油杆部分因惯性继续上行，该部分的自身重力较小，无法抵消其惯性力，导致抽油杆在中和点以下发生过度弯曲，形成“失稳”[4]；

3)在反复弯曲和恢复的过程中，抽油杆的振动频率会逐渐改变并接近外界激振频率，当两者的频率趋于相同时，会产生共振现象，共振会导致抽油杆加速变形。

偏磨现象时常发生，由此导致检泵频率加快、维修支出增加，据统计，该项成本超过总成本的50%[5]，同时也使抽油设施性能下降、寿命减短，严重影响油田的正常产量与经济效益。 偏磨问题是增加生产成本和制约油田采收率提高与稳产的关键技术难题，是限制油田资源开发潜力的主要技术瓶颈。

针对偏磨这一关键技术难题，国内外专家学者对其产生机制及影响因素进行了深入研究，取得了一系列理论与实践成果，为偏磨的有效控制与治理提供了科学依据[6-7]，但这些方法尚不能实时监测偏磨情况，运营人员无法及时发现、处理偏磨问题。 近年来，基于模态分解的故障诊断方法受到了研究者的关注。 1998 年，Huang 等[8]首次提出经验模态分解(EMD)方法，该方法认为任何时间序列都能分解为有限数量的本征模态函数(IMF)之和，但其存在模态混叠问题，应用受到限制。 Wu 等[9]对EMD 进行了改进，提出了集合经验模态分解(EEMD)方法，但该方法在处理噪声较多或低频成分较弱的信号时仍存在模态混叠问题。2014 年，Dragomiretskiy 等[10]提出变分模态分解(VMD)方法，VMD 是一种非递归自适应信号分析技术[11]，该方法可解决信号分解时的模态混叠问题，但需要根据经验设定IMF 分解层数与惩罚因子，这些分解参数的选择对分解效果影响较大[12]。

针对上述不足，本文通过改进人工鱼群算法来优化VMD，并将改进的变分模态分解(IVMD)应用于有杆泵抽油井偏磨程度的诊断。 IVMD 在最佳分解参数下将原始数据分解成多个模态函数，每个模态函数代表不同频率范围内的振动特征，通过对特征的有效提取，为偏磨程度提供可靠的判断依据。 为验证本文IVMD 方法的有效性，采用仿真实验对比分析IVMD 方法与其他方法的诊断结果。

1 改进变分模态分解

1.1 变分模态分解

VMD 的基本原理是:将多个模态函数构成的原始信号Fp(t)分解为N个相互独立的子信号[13]。 VMD 分解得到的IMF 分量表达式为

式中:t为时间变量；un(t)表示第n个IMF 分量(n＝1，2，…，N)，为一个谐波信号；An(t)为un(t)的瞬时幅值；φn(t)为un(t)的瞬时频率。

为实现信号分解，需确定一组模态函数组成，准确地估计每个模态的频带宽度是VMD 要解决的最重要的问题。 VMD 求解过程的约束条件是:各模态函数的带宽总和最小；各模态分量之和等于原始信号，相应的数学描述为

式中:wn表示第n个模态分量的中心频率；δ(t)为信号的残差项。

1.2 改进人工鱼群算法

为获得IMF 分解层数K与惩罚因子β的最佳值，本文采用改进人工鱼群算法对VMD 分解参数进行寻优。

人工鱼群算法通过模拟鱼群行为解决复杂优化问题[14]，包括觅食行为、群聚行为、追尾行为、随即行为[15-17]，该算法收敛慢，且易陷入局部最优难以跳出。 为解决该问题，本文通过改进觅食行为的视野和步长进行优化。

在开始阶段，给予觅食行为较大的视野和步长，并在觅食行为中引入视野衰减因子α(取值范围为0 ～1)和截止因子ε，以加快收敛速度。 当衰减基数α0在0 ～1之间时，α＝ai0，αi0表示第i次迭代的衰减基数；当α＞ε时，第i次迭代的视野Vi为初始视野V0的α倍，即Vi＝α·V0；当α≤ε时，视野不再衰减，Vi为V0的ε倍，即Vi＝ε·V0。 随着迭代的进行，视野逐渐减小，直至达到稳定值。

在循环迭代的同时，觅食行为的步长也随视野变化。 改进的步长Si计算式为

式中:S0为初始步长；φ为视步联合系数，取值为0 ～1。

1.3 基于改进人工鱼群算法优化的VMD 算法

首先对改进人工鱼群算法进行初始化设置，随机产生一定数量的初始种群，将VMD 分解结果中不同频率分量的包络熵值、能量误差作为适应度函数，对每个位置的人工鱼进行VMD 运算并计算初始适应度值。 然后更新人工鱼的位置，寻找VMD 算法的最优分解参数，达到最大迭代次数时停止更新，输出最优参数值，设最优参数组合为(K，β)。

根据唐贵基等[18]提出的包络熵概念，原始信号经VMD 算法分解后得到IMF 分量的包络熵Bn可表示为

式中:a(n)为un(t)经Hilbert 解调后得到的包络信号；Pn为a(n)的归一化形式。 经VMD 算法分解后得到的IMF 分量中若包含的周期性故障特征信息较多，包络熵值较小，反之则信号呈现较弱的稀疏性，包络熵值较大。

为进一步提高诊断效率及准确性，弥补传统目标函数仅能反映信号周期特性而无法反映摩擦特性的不足，本文对仅以熵值为目标函数的传统优化方法进行修正，在目标函数中引入对摩擦信号变化较为敏感的能量误差指标，以更适于摩擦诊断。 能量误差δE计算式为

式中:Ef为分解信号的能量；En为模态函数的能量。δE越大，表示模态函数的能量和越大，端点效应越强，分解效果越差，易出现虚假成分。

将包络熵和能量误差两种指标进行融合可以更好地对振动信号中的偏磨特征进行提取。 本文改进人工鱼群算法的综合目标函数C可表示为

基于改进人工鱼群算法优化的VMD 算法具体优化步骤如下。

1)初始化设置。 选定惩罚因子β及分解层数K各自的搜索范围及搜索步长。 以[Wβ，Uβ]和Sβ分别表示β的搜索范围及步长，以[WK，UK]和SK分别表示K的搜索范围及步长。

2)在单一参数组合形式下，以人工鱼的位置(K，β)为优化参数，根据综合目标函数C评估每条人工鱼的适应度，并标记全局最优解所对应的位置。

3)判断人工鱼位置是否降低综合目标函数值。 如果是，选择该个体；否则进行觅食，以找到更优值。

4)更新人工鱼的位置，并判断迭代次数是否达到最大。 若是，给出对应参数；否则，跳转到步骤2)(每循环一次，迭代次数增加一次)。

参数值优化结果如图1 所示，图中黑色圆点对应的坐标即为最优参数组合(K，β)。

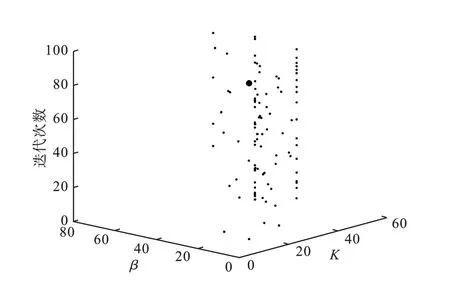
图1 参数值优化结果Fig.1 Optimization results of parameters

2 仿真研究

2.1 改进变分模态分解

为验证IVMD 方法的有效性，本文构建了电参数信号常见的两种异常情况(X1为噪声、X2为间断信号)，进行仿真分析，并与VMD 方法对比。仿真信号X1(t)由X11(t)、X12(t)和X13(t)组成，其时域波形如图2 (a) 所示。 采样频率为1 000 Hz，采样点数为1 500。

图2 时域仿真信号波形Fig.2 Time domain simulation signal waveform

仿真信号X2(t)由X21(t)、X22(t)和X23(t)组成，其时域波形如图2(b)所示。

含随机噪声信号的仿真信号X1(t)的4 层VMD 分解结果如图3 所示，可见，虽然噪声部分被分解，但因分解层数错误导致出现混叠。X1(t)的3 层IVMD 分解结果如图4 所示，可见，三种信号均被有效分离。

图3 信号X1(t)的VMDFig.3 VMD of signal X1(t)

图4 信号X1(t)的IVMDFig.4 IVMD of signal X1(t)

含间断信号的仿真信号X2(t)的4 层VMD分解结果如图5 所示，可见，由于分解层数错误，X2(t)中的一个信号被错误地分成两个子信号，从而导致丢失重要信息或对原始数据特征进行错误判断，引起信号混淆和失真。X2(t)的3 层IVMD分解结果如图6 所示，可见三种信号均被有效分离。

图5 信号X2(t)的VMDFig.5 VMD of signal X2(t)

图6 信号X2(t)的IVMDFig.6 IVMD of signal X2(t)

2.2 信号筛选

为便于后续分析处理，需要根据信号的IVMD 结果筛选出蕴含丰富摩擦特征信息的IMF分量。 各IMF 分量的时域波形差别不大，很难直观断定哪一分量的故障特征最为明显。 为此，计算IMF 分量的峭度值，据其对各分量进行衡量、评价。

图7(a)为信号X1(t)各IMF 分量的峭度值，可见IMF3 分量的峭度值明显高于其他分量，因此将其视为故障分量并进行包络谱分析，其包络谱如图7(b)所示。 由图7(b)可见，谱图中存在一个明显的谱峰，该峰对应于噪声信号中特定的频率。

图7 信号X1(t)的IMF 分量筛选Fig.7 IMF component screening of signal X1(t)

图8(a)为信号X2(t)各IMF 分量的峭度值，可知X2(t)的故障分量为IMF3，其包络谱如图8(b)所示。 图8(b)中的谱图由多个频率不同的正弦波组合而成，亦可见对应于特定频率的谱峰。

图8 信号X2(t)的IMF 分量筛选Fig.8 IMF component screening of signal X2(t)

可见，由于噪声信号、间断信号的非周期性，IVMD 能够从信噪比较低的原信号中有效剥离出包含丰富故障特征信息的信号分量，继而实现微弱特征频率成分的准确提取。

对比不同的分解方法，计算各方法的能量误差，结果如表1 所示。 由于IVMD 拥有智能算法，其分解层数最佳，故能量误差最小。

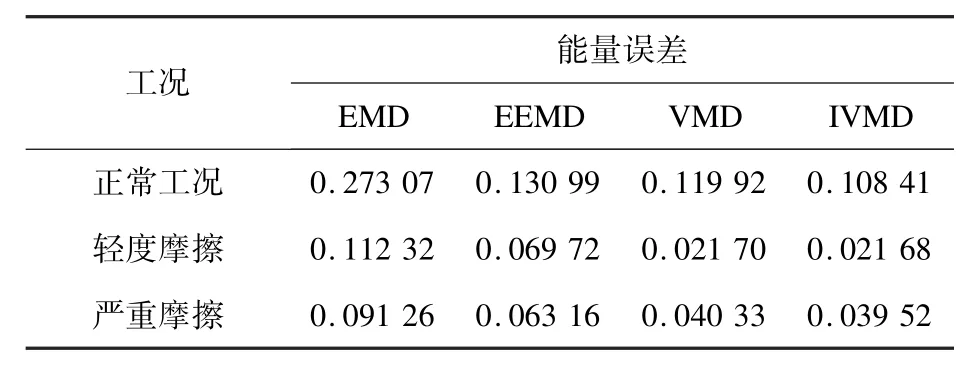
表1 不同分解方法的误差比较Table 1 Comparisions of errors of different decomposition methods

3 试验研究

为进一步验证基于IVMD 的抽油井偏磨程度诊断方法的可靠性，本文以某油田现场监测的电参数信号开展试验(现场共136 口抽油井，其中正常井131 口，故障井5 口)。 与现场实际情况对比，本文方法诊断结果符合率为100%。 下文以其中3 口抽油井为例进行分析说明。

试验抽油井如图9 所示。 通过监测抽油系统工作参数的变化，可以验证抽油杆和油管是否存在偏磨，并确定偏磨程度。

图9 试验抽油井Fig.9 The tested pumping well

采样频率为1 kHz、采样点数为800 时，不同偏磨程度的电参数信号如图10 所示。

图10 不同偏磨程度的电参数信号Fig.10 Electrical parameter signal under different degrees of eccentric wear

当电参数信号如图10(a)所示时，抽油杆扭矩和轴向位移保持平稳，出口油温和油管温度处于正常工作温度，泵功率和出油量处于允许范围内，各参数无明显变化，表明抽油杆和油管基本无磨损和阻塞，工作正常。 当电参数信号如图10(b)所示时，抽油杆扭矩和轴向位移略有波动但变化幅度可接受，出口油温和油管温度略有上升但高温区较小，泵功率和出油量略有变化但影响不大，表明抽油杆和油管出现轻微磨损或局部阻塞，但对工作影响较小，需继续监控。 当电参数信号如图10(c)所示时，抽油杆扭矩和轴向位移变化较大，出口油温较高，油管高温区较大且持续上升，泵功率升高且出油量下降较多，表明抽油杆和油管出现较严重磨损，需要进行检修。

不同偏磨程度的电参数信号IVMD 分解图和峭度图如图11 所示。

图11 不同偏磨程度的电参数信号IVMD 分解图与峭度图Fig.11 IVMD decomposition diagram and kurtosis diagram of electrical parameter signal under different degrees of eccentric wear

由图11 可以看出，图11(a)中的IMF2、图11(b)中的IMF5、图11(c)中的IMF6 在各自峭度图中的峭度值最大，故以此信号进行后续研究。

偏磨信号中的频谱成分与摩擦程度有着密切的对应关系。 Hilbert 变换可以精确分离出偏磨信号的各个频率成分，并计算每个频率成分的幅值，幅值大小代表信号强度，与摩擦程度相对应。RGB 图像技术可将偏磨信号的不同频率成分映射到不同的颜色，颜色的深浅代表幅值的大小，并与摩擦程度相对应。 因此，可采用RGB 图像对信号进行特征提取和处理，以有效识别油井的偏磨程度。

不同偏磨程度的电参数信号VMD-Hilbert(RGB)图如图12 所示，图中横坐标表示无量纲化时间，纵坐标表示无量纲化瞬时频率，不同颜色则代表幅值大小。 当信号受到摩擦力影响时，振动会逐渐衰减，系统的能量降低，振幅会逐渐减小，同时振动频率也会减小，导致幅值减小。 图12(a)中可见多处黄色部分(幅值较大)、鲜绿色部分(幅值中等)；图12(b)中黄色部分、鲜绿色部分减少，深蓝色部分(幅值较低)增加；图12(c)中大部分呈现深蓝色。

图12 不同偏磨程度的电参数信号VMD-Hilbert(RGB)图Fig.12 VMD-Hilbert(RGB)diagram of eletrical parameter signal under different degrees of eccentric wear

上述判断偏磨状态的结果与现场试验结果基本一致，可见，VMD-Hilbert(RGB)方法不仅使数据更加醒目、易于区分，同时能够精准地识别抽油井偏磨程度，通过可视化方式呈现出数据的信息，为设备维护提供依据。

4 结论

传统的油井偏磨程度诊断方法不适用于油田生产需求，故本文提出了基于IVMD 的油井偏磨程度诊断方法，并进行仿真分析及试验验证。 首先采用改进人工鱼群算法优化VMD 的分解层数，进行IVMD 分解， 然后基于VMD-Hilbert(RGB)进行偏磨程度诊断。 利用所提出的方法对不同偏磨程度的油井进行了试验研究，结果表明，IVMD 能够有效地选取最优参数，分解出电参数信号的固有模态，并通过VMD-Hilbert(RGB)图区分抽油井偏磨的严重程度。 IVMD 在参数选择、计算效率和理论完备性等方面均优于传统的VMD，在偏磨程度诊断领域具有广泛的应用潜力。