四旋翼无人机模糊PID控制器设计与仿真
2024-01-10杨永琳孙晋亮孙雪雁朱山川
杨永琳,孙晋亮,孙雪雁,朱山川
(滁州职业技术学院,安徽 滁州 239000)
一、引言
近年来,随着科学技术的不断发展,四旋翼无人机因其体积小、结构简单、性价比高、便于控制等特点被广泛应用于军事行动和民事行动中[1]。但四旋翼无人机是一个具有多变量的非线性系统,易受外界环境的干扰,因此设计出一种能够保证稳定飞行且具有良好控制效果的控制器是当前四旋翼无人机研究的热点。
目前应用于四旋翼无人机控制器上的算法主要包含:1)传统PID控制[2];2)反演控制法[3];3)滑模控制法[4];4)动态逆方法[5];5)神经网络控制[6]等。控制器中所选用控制算法决定了四旋翼无人机在飞行中的稳定性和自适应性。传统PID算法是利用P(比例)、I(积分)、D(微分)三种方法结合在一起,利用各自的优缺点进行互补从而实现快速达到控制目标的一种控制算法,因其具有简单方便且易于实现等特点,是目前工业控制中最常用的控制方法。但传统PID控制算法需要人为进行多次试凑来实现参数的调整,对于飞行环境发生变化的情况下原有参数就无法达到最优控制效果,则需要重新试凑调整参数以达到控制目的,因此文中主要针对传统PID控制算法调参困难的问题,在传统PID控制环节加入模糊控制规则构成模糊PID控制器从而达到参数自整定的目的,使四旋翼无人机能够更加快速地达到预期目标位置。最后,在MATLAB/Simulink仿真环境中针对所设计模糊PID控制器进行相关实验和仿真验证。
二、建立数学模型
四旋翼无人机从外观上看拥有对称性的静态特性,但它的数学模型却是一个具有4个输入6个输出的非线性动态系统。一个良好的控制器应该确保被控对象在达到预期位置的同时能够保证系统的快速稳定性。
(一)定义混合坐标系
目前主流的四旋翼无人机在机体结构上大致分为“+”字型结构与“×”型结构[7],文中以“+”字型的四旋翼无人机为对象进行建模研究。由于四旋翼无人机是一个具有强耦合性的欠驱动系统,因此建模时需要先确定坐标系:机体坐标系b与地理坐标系e[8],如图1所示。定义机体坐标系b的三个坐标轴分别为:以机体重心为坐标原点,X轴与机身平行且以指向机头方向为X轴正方向,Z轴垂直于X轴向上,位于机体的垂直对称面内,Y轴则与OXZ面相垂直;定义地理坐标系e为:以地球圆心作为坐标原点,由原点指向东边为X轴正方向,原点指向北边为Y轴正方向,Z轴垂直于OXY面指向天。在机体坐标系中分析四旋翼无人机所做的旋转运动,在地理坐标系中分析位置运动。
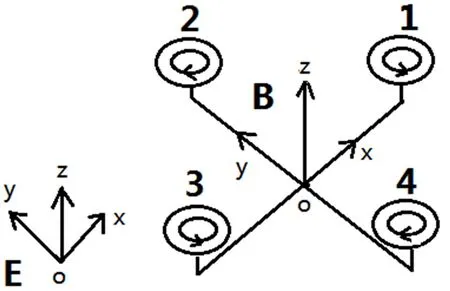
图1 混合坐标系定义
四旋翼无人机的滚转角φ定义为无人机在机体坐标系中绕OX轴所做的旋转运动;绕OY轴的旋转运动为俯仰角θ;绕OZ轴的旋转运动为偏航角ψ。当忽略地球自转时,地理坐标系与惯性坐标系相重合,此时地理坐标系与机体坐标系之间可以相互转换,转换矩阵如下[8]:
(二) 建立模型方程
四旋翼无人机有6种运动状态:上下、左右、前后运动和俯仰、偏航、滚转运动。由此有6个输出,为x、y、z位置的位移信息和滚转角φ、俯仰角θ、偏航角ψ。此外其有4个输入:升力T、滚转力矩τφ、俯仰力矩τθ、偏航力矩τψ。由此建立输入系统的数学模型:
式中,Ct为升力系数、ω为电机的转速、Cq为扭矩系数、l为电机到机体中心的距离。
在建立四旋翼无人机运动学方程时需做出如下假设[9]:
1)机体坐标系原点与机身质心重合。
2)四旋翼无人机质量分布均匀,结构完全对称,忽略弹性变化。
3)不考虑陀螺效应、机体摩擦影响。
4)忽略地球曲率即地球表面为平面。
由牛顿力学定律和转动力学定律可得数学模型方程[10]:
(1)
式中,ωr=-ω1+ω2-ω3+ω4,vx、vy、vz分别为x、y、z轴线速度,p、q、r分别为滚转角角速度、俯仰角角速度以及偏航角角速度。
三、模糊PID控制器
模糊PID控制器主要分为模糊推理和PID控制两个部分。PID控制算法在闭环系统中应用时,它所接收的输入信号为预期值与被控对象输出值之间的误差e,然后通过比例控制、积分控制和微分控制求得系统的控制律,从而实现控制目标。模糊PID控制器则是在PID控制的基础上利用模糊规则对其控制参数进行自整定从而使系统更加快速地达到最优解。其控制结构图如图2所示。
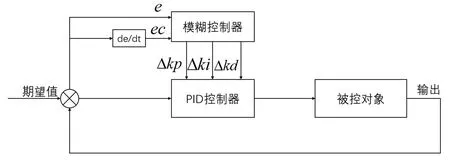
图2 模糊PID控制系统结构图
由图可见,模糊PID控制器有两个输入:设定的系统期望值和系统输出值之间的误差e和误差变化率ec,然后利用事先设定的模糊控制规则表进行模糊推理,得到PID控制器的三个参数增量Δkp、Δki、Δkd,最后将这三个增量整合到PID控制器中即可得到自整定参数的PID控制系统。
(一) PID控制
PID控制器由比例环节(P)、积分环节(I)、微分环节(D)构成[10]。被控对象经PID控制算法解算后的控制律可表示为:
(2)
式中,Kp为比例系数,Ti为积分时间常数,Td为微分时间常数,e(t)为系统预期值与系统输出值之间的误差。
(二) 模糊推理
模糊控制的核心在于利用专家对被控对象的控制经验和相关理论知识编写模糊控制规则以及确定模糊推理算法[11]。
模糊控制器的控制步骤为:首先需要确定控制器的输入和输出变量,然后由确定的隶属度函数将输入的清晰量进行模糊化处理,然后通过模糊规则表进行模糊推理得到输出的模糊量,最后对推理得到输出模糊量进行解模糊,变成清晰量之后再传输到被控对象中,从而控制被控对象达到预期目标。
四、仿真分析
首先在MATLB/Simulink仿真环境中搭建四旋翼无人机的动力学模型,然后将设计好的模糊PID控制器应用到四旋翼无人机控制回路中并进行仿真。
设定姿态控制系统中滚转角、俯仰角、偏航角的初值以及角速率初值为:
x、y、z轴位置初值为:
预期达到的目标位置与偏航角设定为:
xd=yd=1,zd=2,ψd=1;
针对模糊控制器的两个输入e和ec以及三个输出Δkp、Δki、Δkd选择相同的模糊子集:{NB,NM,NS,ZO,PS,PM,PB},其分别表示“负大、负中、负小、零、正小、正中、正大”。输入输出论域设定为{-6,6},隶属度函数选择使用三角函数。在MATLAB仿真环境中的相关设置如图3所示。

图3 模糊控制设置图
在仿真环境中设定好相关的模糊控制规则后,将模糊控制加入到PID控制中形成模糊PID控制器,此时PID控制的三个控制参数kp、ki、kd的值则是由初始值与模糊控制得到的增量相互整合后得到,即:
(3)
设定传统PID控制器的各通道的原始参数为:Kpx0=2轴参数为Kpx0=2,Kix0=0.001,Kdx0=2;Kpy0=2轴参数为Kpy0=2,Kiy0=0.001,Kdy0=2;Kpz0=2轴参数为Kpz0=2,Kiz0=0.001,Kdz0=2.5;偏航角参数为Kpψ0=3,Kiψ0=0.001,Kdψ0=3;将仿真时间ψ设置为ψ。
图4给出了四旋翼无人机在Matlab仿真环境下传统PID控制器与模糊PID控制器分别对飞行控制系统进行控制的仿真结果,由图可得,在无干扰情况下,传统PID控制器达到x、y、z轴给定位置分别需要7S、8S、4S左右,而模糊PID控制器则分别只需要3S、5S、3S即可达到x、y、z轴给定位置;对于偏航角而言传统PID控制器需要3S达到稳态,而模糊PID控制器只需要2S即可达到稳态,因此模糊PID控制器能够使系统更加快速地达到给定位置;在位置运动上模糊PID控制器的上升时间大约为2S,而传统PID控制器则需要4S,且模糊PID控制器的超调量和稳态误差要更小。
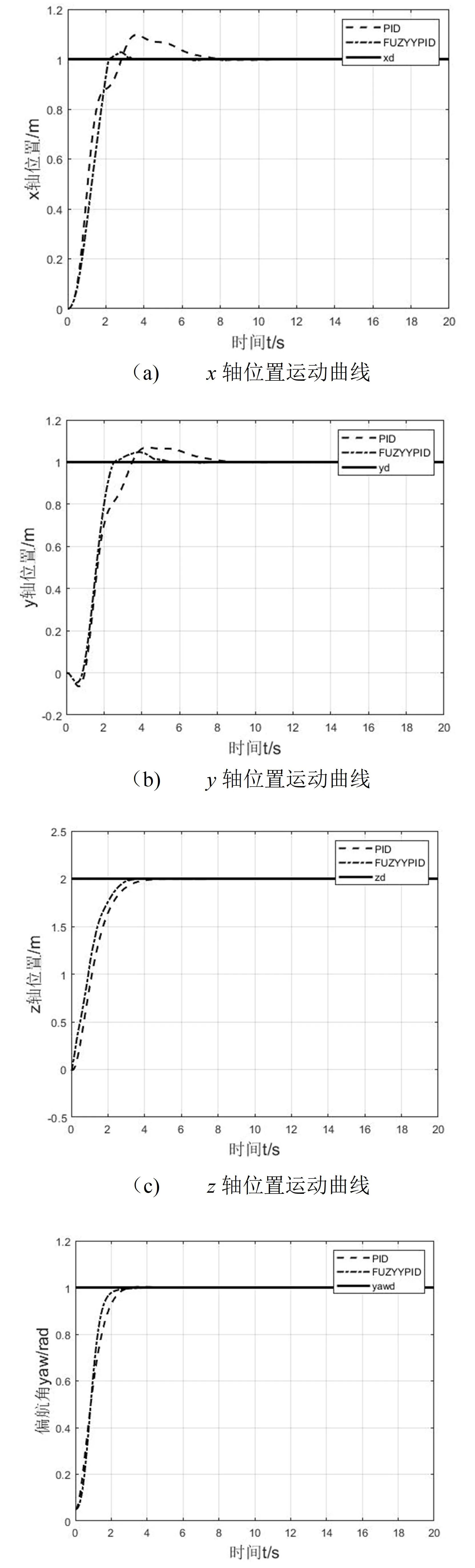
图4 模糊PID与传统PID对比曲线图
由此可见,传统PID控制器控制的四旋翼无人机飞行系统在飞行过程中由于调整参数困难,无法快速求解最优解,使系统会出现大幅超调,调节时间长。而文中设计的模糊PID控制器能够更加快速地调整系统控制参数,从而更加有效地控制系统达到预期目标位置,且同时能够保证飞行过程中姿态角的稳定性。
五、结束语
文中利用牛顿力学定律和转动力学定律对四旋翼无人机的飞行状态进行分析解算得出四旋翼无人机的数学模型,并且针对传统PID控制算法在多变的外界环境中无法快速调参的问题设计了模糊PID控制器,最后通过MATLAB/Simulink仿真环境搭建飞行控制系统模型,通过与传统PID控制器的控制仿真结果对比表明,模糊PID控制器能够更加快速地达到系统预期值并且能够保证飞行过程中姿态控制的稳定性。
