基于同态滤波耦合的低照度图像超分辨率重建算法

王叁军

(广州城建职业学院 继续教育学院,广东 广州 510925)

从自然环境中获取图像,经常受到光照、气候、地理等因素影响,同时图像采集设备也会由于抖动、系统干扰等问题导致所获取的图像存在较为明显的噪声干扰,严重时会出现图像对比度降低、颜色失真等质量问题[1]。如果图像分辨率较低、质量较差,将会严重影响与该图像相关的后续工作开展。例如电力系统巡检工作需要利用无人机采集电力线路的图像[2-3],通过分析无人机采集的图像获取电力系统的安全情况,这种从户外采集的图像,经常受到恶劣天气的影响,导致图像模糊不清,图像中的内容会出现严重灰白色,发生颜色失真;还有应用于监控设备的图像也会受到多种因素影响发生失真[4-6]。如果图像采集设备在大风环境中会发生抖动,在夜间环境中清晰度会降低,如果受到浓雾天气影响,将无法准确获得需采集的内容[7]。由此可以看出,提升图像质量、消除干扰信息、获得高分辨率图像,是目前有关行业重点需要研究的问题。

王通等[8]研究人员使用优化后的U-Net神经网络的稀疏视角实现图像质量提升,该算法能够实现低质量图像的重建,获得效果更好的图像结果,但是不能消除图像上的噪声干扰,所以图像质量提升效果并不优异。陈瑞娟等[9]学者利用图像融合算法提升图像的质量,该算法先分割原始图像,得到图像结构信息,使用灵敏度矩阵算法重建图像,最后使用小波融合算法获得融合后的图像,该种算法能够凸显出众多细节信息,但是图像的分辨率依旧不是很好。

同态滤波能够解决图像上细节模糊以及光晕干扰的问题,利用同态滤波处理原始图形,消除图像上的噪声,提升图像的对比度,提升图像的质量,以便后续重建图像工作的开展[10-11]。本文使用同态滤波耦合算法,结合灰度变换优化后的卷积神经网络,输出超分辨率重建的图像。

1 低照度图像超分辨率重建算法

1.1 基于同态滤波耦合的低照度图像对比度增强

同态滤波耦合以光照反射模型为基础,反射成分p(x,y)和照度成分q(x,y)相乘,获得图像f(x,y):

f(x,y)=q(x,y)×p(x,y)

(1)

其中,q(x,y)属于缓慢变化,主要用于描述低照度图像中的低频成分,该成分能够反映出图像中的亮度特征;p(x,y)属于剧烈变化,用于描述低照度图像中的高频成分,主要可以表征图像内的边缘细节特征与噪声特征。

对数运算处理f(x,y),式(1)中q(x,y)与p(x,y)的关系为相乘,对数运算时,将该关系转化为相加:

lnf(x,y)=lnq(x,y)+lnp(x,y)

(2)

使用傅里叶变换处理式(2):

F{lnf(x,y)}=F{lnq(x,y)}+F{lnp(x,y)}⟺F(u,v)=Q(u,v)+P(u,v)

(3)

其中,F{·}用于表示傅里叶变换,q(x,y)、p(x,y)与f(x,y)发生傅里叶变换后转变为Q(u,v)、P(u,v)和F(u,v)。

H(u,v)为同态函数,滤波处理式(3)后获得式(4):

H(u,v)F(u,v)=H(u,v)Q(u,v)+H(u,v)P(u,v)⟺HF(u,v)=HQ(u,v)+HP(u,v)

(4)

对式(4)开展傅里叶反变换,该变化需要使用F-1{·}完成处理,式(5)为傅里叶反变换:

F-1{HF(u,v)}=F-1{HQ(u,v)}+F-1{HP(u,v)}⟺hf(x,y)=hq(x,y)+hp(x,y)

(5)

指数变换式(5)的两侧,通过计算获得对比度提升后的低照度图像g(x,y):

g(x,y)=exp|hf(x,y)|=exp|hq(x,y)|×

exp|hp(x,y)|

(6)

提升低照度图像对比度的关键步骤,就是将原始低照度图像中的P(u,v)成分升高同时降低Q(u,v)成分,该过程中,可以将同态函数H(u,v)看成是一个高通滤波器。

虽然经过以上过程处理,能够提升低照度图像的对比度,但是并不能完全保留低照度图像上的细节特征,所以进一步使用中心像素点(u0,v0)和频域像素点(u,v)之间存在的距离D(u,v)建立指数型同态滤波函数:

H′(u,v)=(pH-pL)e[-D0/D(u,v)]2+pL

(7)

其中,D0用于描述截止频率,pH是高频增益,pL用于表示低频增益。假设pH>1,且pL<1,使用H′(u,v)就能够将照度成分降低,使得图像中的反射成分得到提升,滤除图像中的干扰信息,保证低照度图像中的对比度得到提升。

1.2 基于自适应非线性拉伸的低照度图像饱和度提升

尽管经过同态滤波耦合处理后,低照度图像的对比度得以提升,但是这种低照度图像受到图像采集环境的影响,饱和度较低,丧失原本的图像色彩,导致清晰度较差,不利于低照度图像的超分辨率重建,因此本文使用自适应非线性拉伸算法提升对比度增强后低照度图像的饱和度。由于原始图像存在差异,所需拉伸的图像饱和度大小也各不相同,所以选取自使用非线性拉伸算法[12-13],将对比度提升后的低照度图像饱和度提升,计算式见式(8):

Rout={1+mean(R,G,B)/[max(R,G,B)+

min(R,G,B)+1]}Rin

(8)

其中,与同态滤波耦合处理后低照度图像像素点RGB颜色分量相对应的最大值为max(R,G,B);Rout用于代表对比度增强后低照度图像经过饱和度提升之后的结果;mean(R,G,B)是对应同态滤波耦合处理后低照度图像像素点RGB颜色分量的均值;Rin用于表示初始饱和度;min(R,G,B)用于描述图像上像素点颜色分量的最小值。通过该处理,进一步提升低照度图像的饱和度,使得图像的色彩更加鲜明。

1.3 基于改进卷积神经网络的低照度图像超分辨率重建

1.3.1 卷积神经网络网络结构构建

为实现图像超分辨率重建,需要使用卷积神经网络,该网络主要包括三个关键部分,详细结构与作用如下:

1)提取低照度图像特征

对提升对比度与饱和度的低照度图像特征提取时,需要利用卷积神经网络中的卷积核,本文分别选择两种卷积核,一种包含28个卷积核,大小为3×3;另一种也是28个卷积核,大小仍然为3×3,但该卷积核包含两层[14]。这些卷积核与contact共同完成特征提取工作,根据卷积核数量,一共可以获得56个特征图。

2)低照度图像特征映射

经过上文同态滤波耦合处理和自适应非线性拉伸后,低照度图像的对比度与饱和度都得到改善,但是经过处理后,该图像中还是存在部分低分辨率特征情况,对于这部分特征,使用卷积层中的卷积核进行处理,向高分辨率特征映射。该映射过程中,利用两层深度可分离卷积处理数个特征图,卷积核的数量为n个,卷积核的大小按照研究经验初步确定为3×3[15]。

3)分辨率重建

经过以上处理,对比度与饱和度提升后的低照度图像中的高分辨率特征被拓展,这些特征都被放大和重建。选取卷积核大小为9×9,子像素卷积操作这些卷积核与56个特征图,实现对比度与饱和度提升后的低照度图像的超分辨率重建。卷积操作使用的卷积函数如式(9)所示:

Fn(Y)=max{σ×[wn*Fn-1(Y)+Bn],

wn*Fn-1(Y)+Bn}

(9)

通过式(10)实现子像素的卷积操作:

Fn(Y)=U[wn*Fn-1(Y)+Bn]

(10)

其中,Fn(Y)代表卷积层输出的结果;*用于描述卷积操作;wn代表卷积计算中的偏置;Fn-1(Y)用于表述输入到卷积层的特征图;U代表子像素卷积操作;Bn表示卷积核的大小;σ用于代表激活函数ReLU的激活参数。

1.3.2 改进卷积神经网络超分辨率重建

本文研究过程中利用同态滤波耦合与自适应非线性拉伸提升低照度图像的对比度与饱和度,使用灰度变换优化卷积神经网络,将质量较差、分辨率较低的低照度图像通过重建分辨率,提升图像的质量。

该算法过程中对比度与饱和度提升后的低照度图像为输入,使用灰度变换处理这部分输入图像,同时确保利用卷积神经网络训练这部分经过灰度变换之后的图像,经过灰度变换以及训练之后,更利于获得这些图像中的特征。灰度变化时,对于特征进行选择性变化,避免错误提升图像中的无效特征,只针对其中有效的部分特征实现灰度变换,算法的详细过程如下:

Step 1:将对比度与饱和度提升后的低照度图像作为输入,并差异化放大该图像,将该输入标记为x。

Step 2:为提升对比度与饱和度增强后的低照度图像x的特征显示能力,先使用灰度变换方式处理x,再引导x向第一个卷积层前进,x0表示灰度拉伸之后的低照度图像。

(11)

Step 3:首次卷积运算x0,获得首个卷积层的输出y0:

y0=w1*x0+B1

(12)

其式中,w1表示卷积模板;B1代表偏置。

Step 4:针对特征图y0的每一个通道需要开展灰度变换操作,灰度变化后的特征y0变为y1:

(13)

Step 5:二次卷积计算y1,获取第二个卷积层输出y2:

y2=w2*y1+B2

(14)

其中,w2代表二次卷积计算的卷积模板;B2则是二次卷积计算的偏置。

Step 6:继续灰度变换y2内各通道,y2增强后转换为y3:

(15)

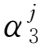
Step 7:第三次卷积运算y3,最终输出超分辨率重建后的图像结果y:

y=w3*y3+B3

(16)

其中,w3表示第三次卷积运算的模板;B3表示第三次卷积运算的偏置。

Step 8:确定如下关系:

(17)

使用式(18)描述等待优化的损失函数Loss(θ):

(18)

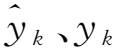
Step 9:循环迭代之前,先对卷积神经网络中存在的参数进行全新变换,获得新的参数,直到停止迭代,或者损失函数符合既定阈值条件就可以停止参数更新。

Step 10:输出低照度图像超分辨率重建结果。

2 重建结果分析

2.1 数据集

为验证本文所研究的超分辨率重建算法的性能,使用较为常见的CIFAR-10/100数据集,该数据集包含电力巡检、交通监控等10个类别,图像的像素均为32×32,属于低分辨率图像,图像数量共525 480幅,其中测试集为112 357幅,训练集为413 123幅。从该数据集中分别选取一幅电力巡检低照度图像和一幅交通监控低照度图像,开展试验分析,二幅图像的原始情况如图1所示。

图1 原始低照度图像

从图1中能够看出,原始图像的照度均较低,对比度和饱和度均较低,图像的清晰度较差,色差较大,需要使用本文方法实现各个低照度图像的超分辨率重建。

2.2 同态滤波耦合处理效果试验

在对低照度超分辨重建之前,本文算法先使用同态滤波耦合处理低照度图像,提升该图像的对比度,处理结果如图2所示。

图2 同态滤波耦合处理效果

由图2可知,使用同态滤波耦合处理各个低照度图像之后,能够提升图像的对比度,消除原始图像的大量噪声信息,凸显出图像上的细节信息,为后续图像超分辨率重建提供便利条件。

2.3 自适应非线性拉伸处理效果试验

原始低照度图像经过同态滤波耦合处理后,低照度图像上的噪声得到消除,对比度发生改善,但是低照度图像上存在的色差问题仍旧较为严重,因此使用本文算法中的自适应非线性拉伸部分,处理同态滤波耦合后的低照度图像,处理结果见图3。

图3 自适应非线性拉伸处理效果

由图3可知,经过自适应非线性拉伸算法处理后各个低照度图像的显色信息得到提升,原始图像缺失的颜色信息得到弥补,使得低照度图像的视觉效果更好。

2.4 超分辨率重建效果试验

低照度图像经过同态滤波耦合处理和自适应非线性拉伸算法处理以后,图像的质量一定程度上得到提升,但是仍然不能满足使用需求,使用本文算法处理各个图像后,实现低照度图像的超分辨率重建,重建结果如图4所示。

图4 超分辨率重建结果

通过图4能够看出,使用本文算法处理后的低照度图像,亮度、锐度等图像特征均得到提升,超分辨率重建的图像,更加清晰,没有再出现明显干扰信息,适合后续工作开展。

2.5 超分辨率重建效果评价

使用峰值信噪比评价超分辨率重建后的低照度图像的质量情况。通常情况下峰值信噪比高,则超分辨率重建后的图像更逼真。峰值信噪比通过式(19)计算获得峰值信噪P:

P=10×lg[(2n-1)2/MSE]

(19)

其中,MSE代表均方误差,n为常数。

为使试验结果更加具有对比性,使用改进的U-Net神经网络算法(文献[8]算法)和图像融合算法(文献[9]算法)同时处理本文所使用的2幅低照度图像,各个算法的重建效果评价结果如表1所示。

表1 峰值信噪比评价结果

由表1可知,使用本文算法处理后的低照度图像,具有更大的P值,说明使用本文算法后,低照度图像更加逼真。与本文算法相比,两种对比算法的峰值信噪比略低,说明在同类算法中,本文算法更加具有优势。

结构相似性也是评价图像质量的一个指标,图像的结构相似度和图像质量之间存在正比例关系。添加噪声干扰,通过试验分析,确定各个算法处理两种低照度图像后,该图像的结构相似性变化情况,结果见图5。

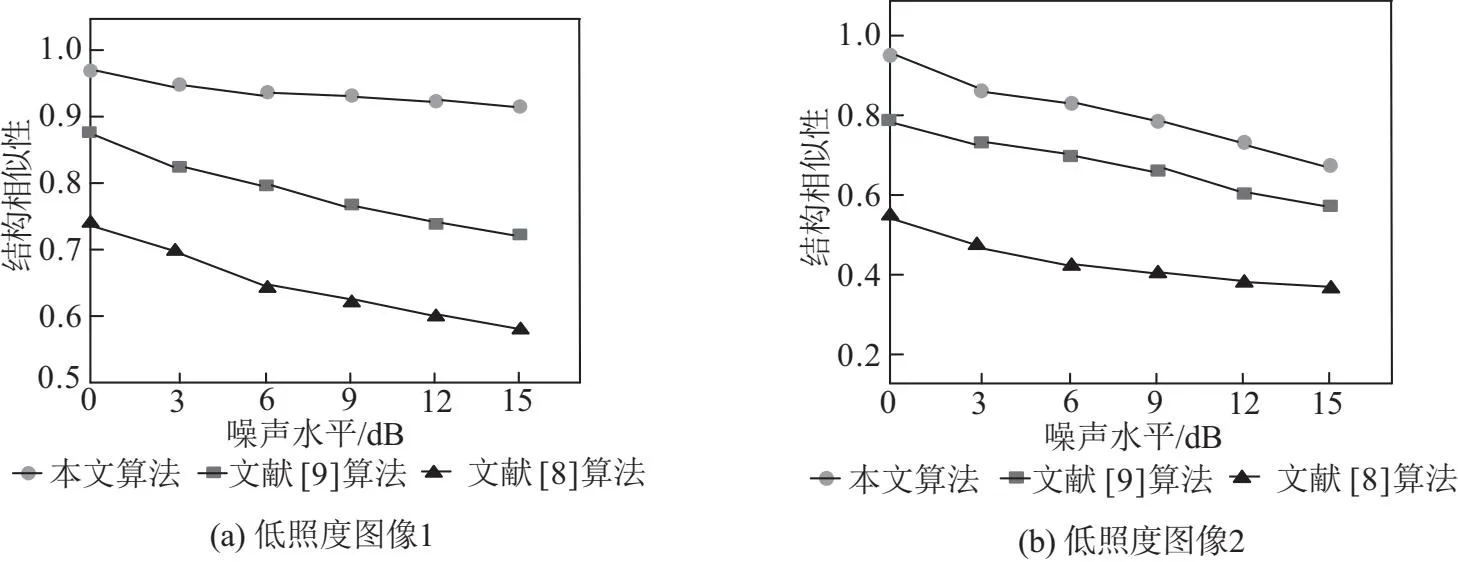
图5 结构相似性对比结果

通过图5可知,受到不同噪声水平干扰,各个算法处理后图像超分辨率重建结果均出现结构相似性降低的变化趋势,由于本文算法使用同态滤波耦合,一定程度降低低照度图像的噪声干扰,所以本文算法重建后的图像始终保持较高水平,没有出现明显畸变。由于低照度图像1上的背景干扰信息较少,因此图5(a)中本文算法处理后的超分辨率图像结构相似性更平稳,结构相似性变化更小。

3 结论

受到多种外部因素的影响,图像采集后照度较低,同时存在对比度、饱和度较低的情况,因此使用基于同态滤波耦合的低照度图像超分辨率重建算法提升图像质量。本文将同态滤波耦合和自适应非线性拉伸算法处理后的低照度图像作为卷积神经网络的输入,结合灰度变换,实现低照度图像的超分辨率重建。实验结果表明:该方法能够消除原始图像上的噪声,保留图像的细节信息,优化图像的质量,结合自适应非线性拉伸算法提升低照度图像的饱和度,使得低照度图像更真实、清晰。