双销式履带板拉伸载荷分布影响因素研究

沈泽华， 王中宝， 牛莉叶， 廖日东

(1.北京理工大学 机械与车辆学院，北京 100081；2.北方车辆集团有限公司，北京 100072)

履带板是履带推进装置的主要组件，其作用是保证车辆在松软地面上的高通过性，降低行驶阻力的同时使其对地面有良好的附着力.通过履带和地面的相互作用，推进装置为履带车提供牵引力和制动力.履带板应在质量较小的条件下具有较高的强度和较长使用寿命[1-2].双销式履带行驶装置主要包括履带板、销轴、端联器、诱导齿以及橡胶衬套[3].

相较于连接部件(端联器、诱导齿)对销轴采用均布载荷分配的方法，文献[4]利用有限元方法进行迭代计算，“两步法”更加准确地计算得到连接部件上的载荷分配比：计算连接部件的刚度，根据履带板对称性采用简化模型，在其对称面设置对称约束，在销轴上施加连接部件的拉伸载荷，经计算得到弹簧反力，将此时的弹簧力施加到销轴上再次迭代计算，弹簧力趋于稳定时即为履带板连接部件的横向载荷，该横向载荷能够更准确地分析端联器和诱导齿的强度.

计算横向载荷分配时迭代两次趋于稳定，分析结果发现诱导齿刚度较小，其所承受的横向载荷占比却更大，横向载荷分布情况极大地影响连接部件的结构强度及其可靠性.

在探究双销式履带板横向载荷占比的影响因素方面，还未曾有人进行研究计算和理论分析.为尽量减小诱导齿所受的横向拉力，改善其受力条件，满足零件可靠性，文中从拉伸载荷分布的影响因素入手[5-6]，使用履带板有限元模型进行迭代计算，研究连接部件结构尺寸变化对载荷分配的影响[7-9].对双销式履带板进行力学分析[10]建立理论计算模型，得到载荷分配与连接部件刚度的关系，进一步验证有限元计算模型的可信度.

1 履带板拉伸载荷分配有限元计算

1.1 有限元迭代计算

双销式履带板模型如图1所示.首先对端联器、诱导齿施加拉伸载荷和与载荷相同方向的位移约束分别计算其横向拉伸刚度，并在三节履带板1/4模型中采用弹簧单元代替连接部件，弹簧刚度为对称模型中连接部件的等效刚度.

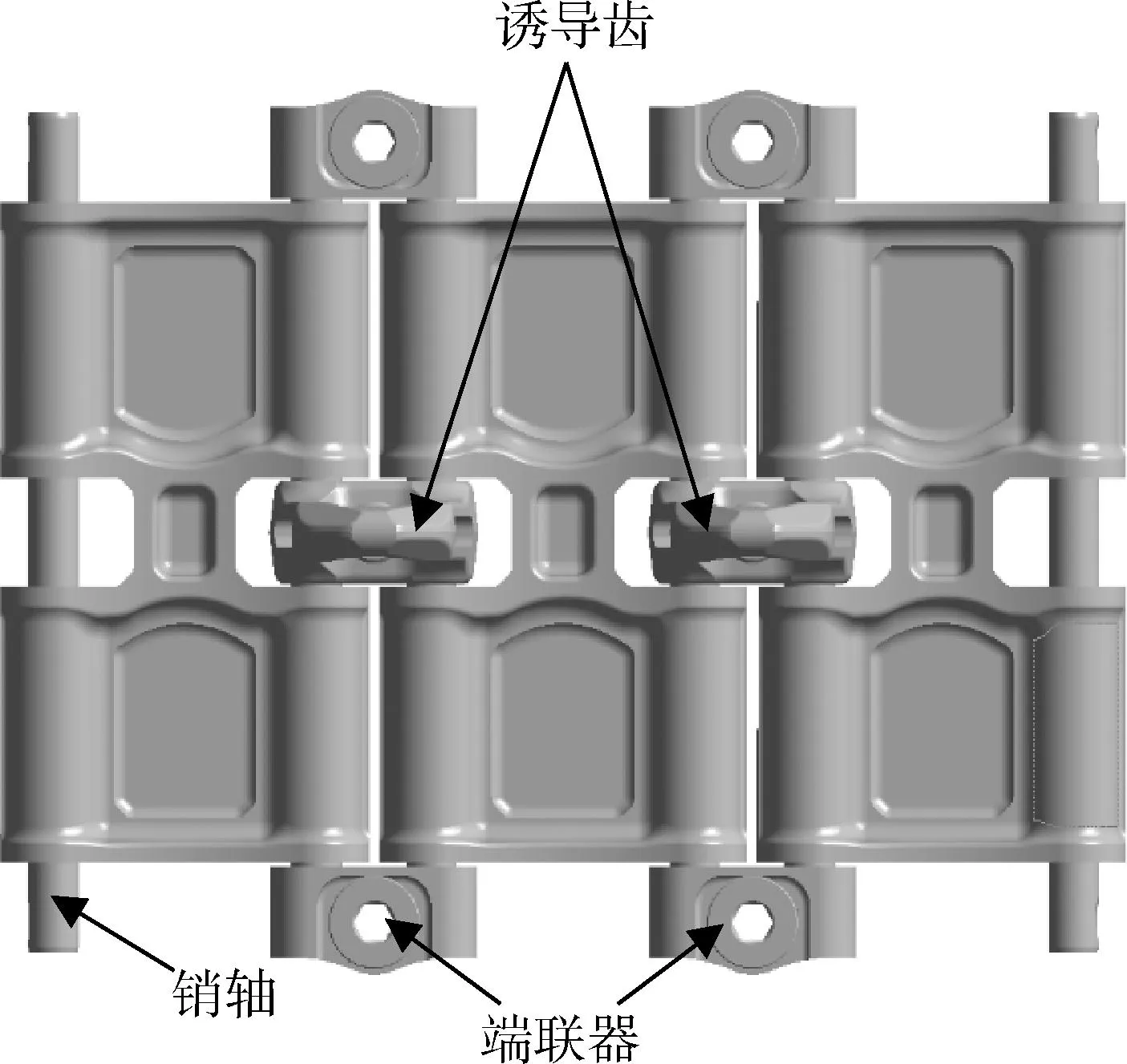
图1 双销式履带板模型

履带最大牵引力计算公式[11]

Pmax=0.65mgφ，

(1)

式中：m为履带车辆的总体质量，kg；g为牵引力加速度，m/s2；φ为履带对地面附着系数，通常取φ=0.8～1.0.

针对某型号装甲车履带板进行有限元计算，其所受到最大牵引力为91.726 kN，模型如图2所示，网格单元尺寸为1 mm.

图2 履带板有限元计算模型

在履带板与负重轮接触面上施加竖直方向车重，按照连接部件刚度比施加横向载荷，端联器等效连接刚度K1为990.411 kN/mm，诱导齿等效连接刚度K2为119.154 kN/mm，刚度比为8.31∶1，在对称模型中诱导齿为原模型一半，其等效弹簧刚度为59.577 kN/mm.迭代示意图如图3所示.

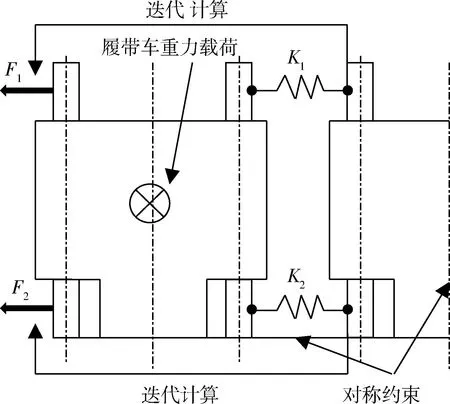
图3 三节履带板1/4模型迭代示意图

对称模型受到的拉伸载荷为45.864 kN，端联器拉力F1=43.261 kN，诱导齿拉力F2=2.603 kN.

迭代计算后连接部件横向载荷分配趋于稳定，如图4所示.得到诱导齿所承受的横向载荷占比为61.99%，单个端联器占比为19%.

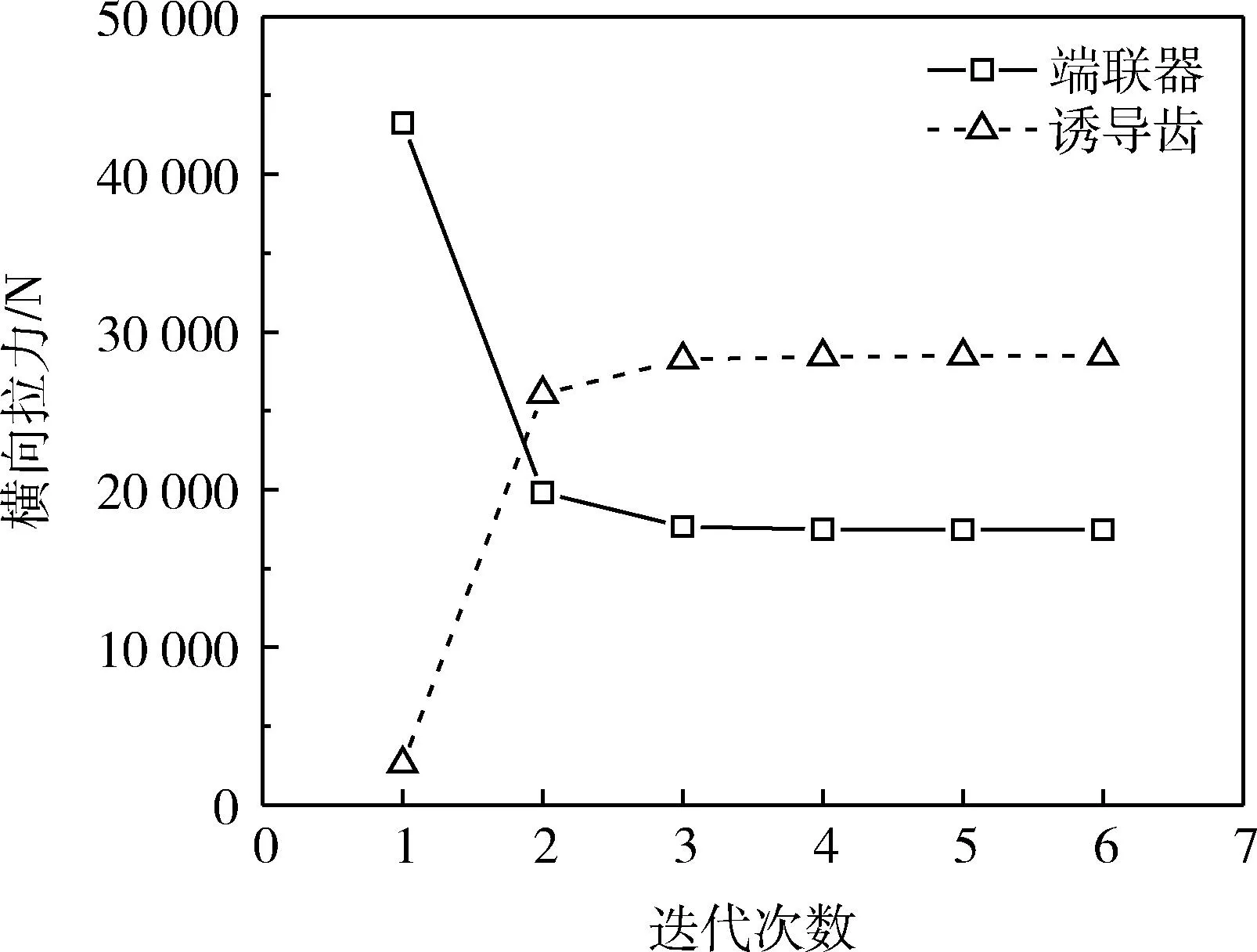
图4 横向载荷迭代计算结果

1.2 连接部件刚度对载荷分配的影响

为探究拉伸载荷分布的影响因素，该节分析讨论连接部件(端联器、诱导齿)刚度与销轴弯曲刚度对横向载荷分配的影响.分别改变端联器、诱导齿等效弹簧单元的刚度和销轴的弹性模量，采用有限元模型仿真计算得到诱导齿横向载荷占比的变化规律.

在探究端联器刚度对载荷分配影响时，设置诱导齿的刚度为原模型的59.577 kN/mm，等差增大端联器刚度.同理，在探究诱导齿刚度对载荷分配影响时固定端联器刚度为990.411 kN/mm，等差减小诱导齿刚度.计算得到不同刚度下横向拉伸载荷占比结果如图5所示.统一采用端联器与诱导齿刚度比作为横坐标.由图可知，端联器与诱导齿刚度比越大，诱导齿横向载荷占比减小.增大端联器刚度对横向载荷分配影响较小，减小诱导齿刚度使其所承受的横向载荷占比变化趋势更加明显.

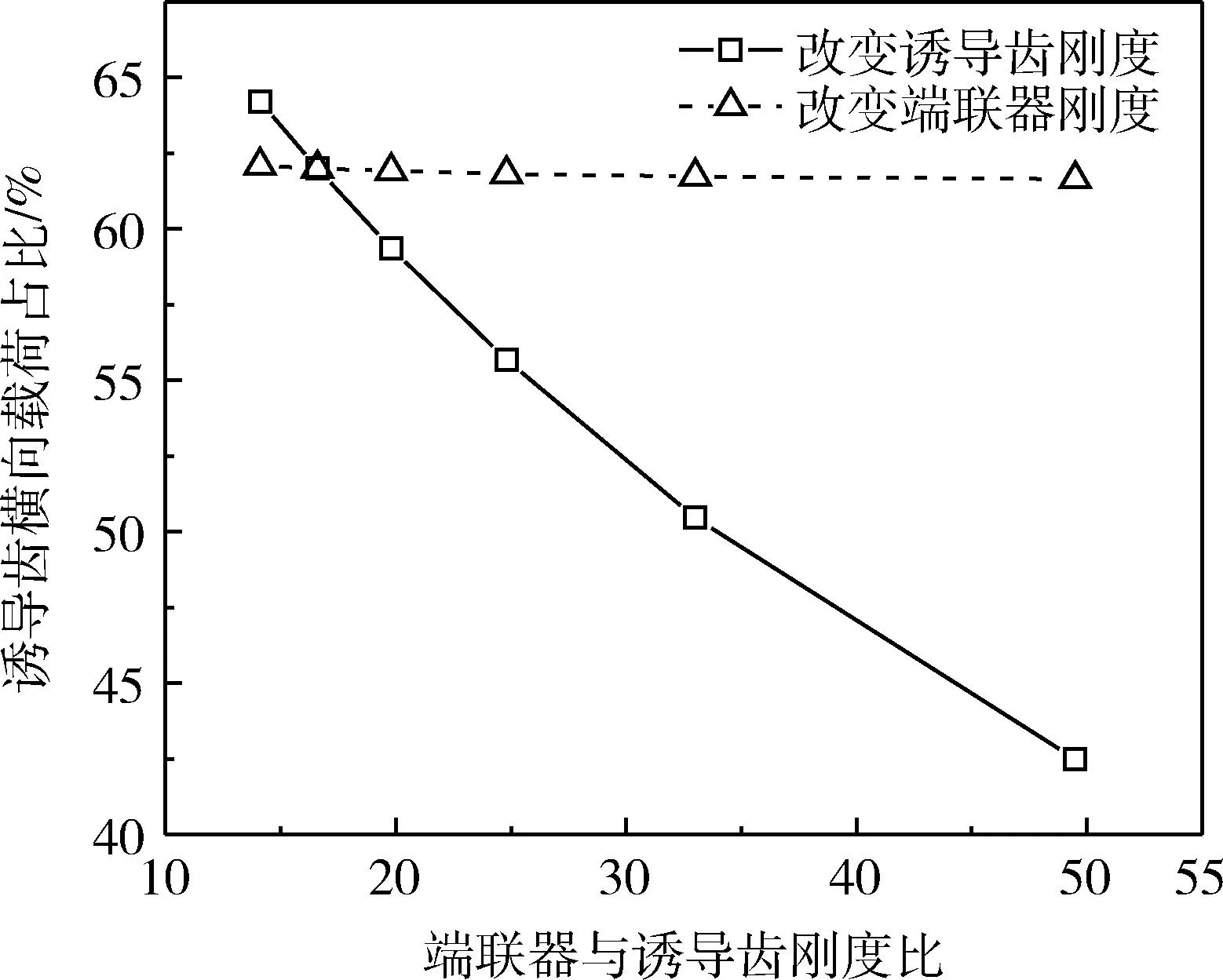
图5 连接部件刚度比与横向载荷分配关系图

为进一步探究连接部件刚度对载荷分配的影响，通过大量有限元仿真计算得到端联器刚度、诱导齿刚度与诱导齿横向载荷占比关系.采用非线性曲面拟合中的ExtremeCum模型得到三者拟合曲面图，如图6所示，其中x、y轴分别为端联器、诱导齿刚度，z轴为诱导齿横向载荷分配占比.

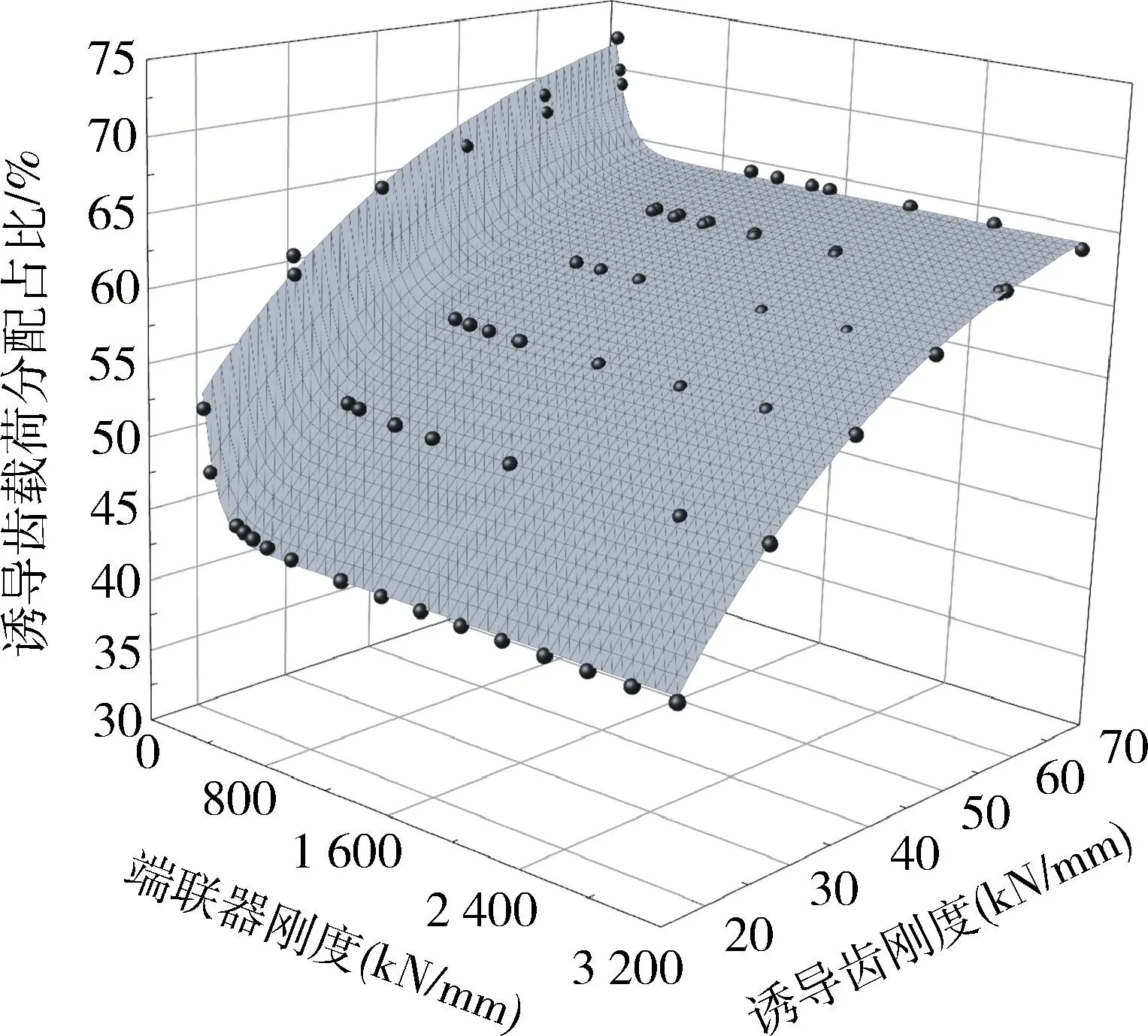
图6 诱导齿载荷分配曲面图

拟合方程表达式：

(2)

从图6可知，诱导齿刚度不变，端联器刚度增大或端联器刚度不变，诱导齿刚度减小时，诱导齿横向载荷占比均减小，且连接部件刚度对横向载荷分配的影响规律不同.端联器刚度较小时其对横向载荷分配的影响更为明显.

1.3 销轴刚度对载荷分配的影响

履带板销轴弯曲刚度也影响履带板横向载荷分配，将销轴轴径固定不变，改变销轴材料的弹性模量，得到诱导齿载荷分配占比与销轴刚度的关系，如图7所示.

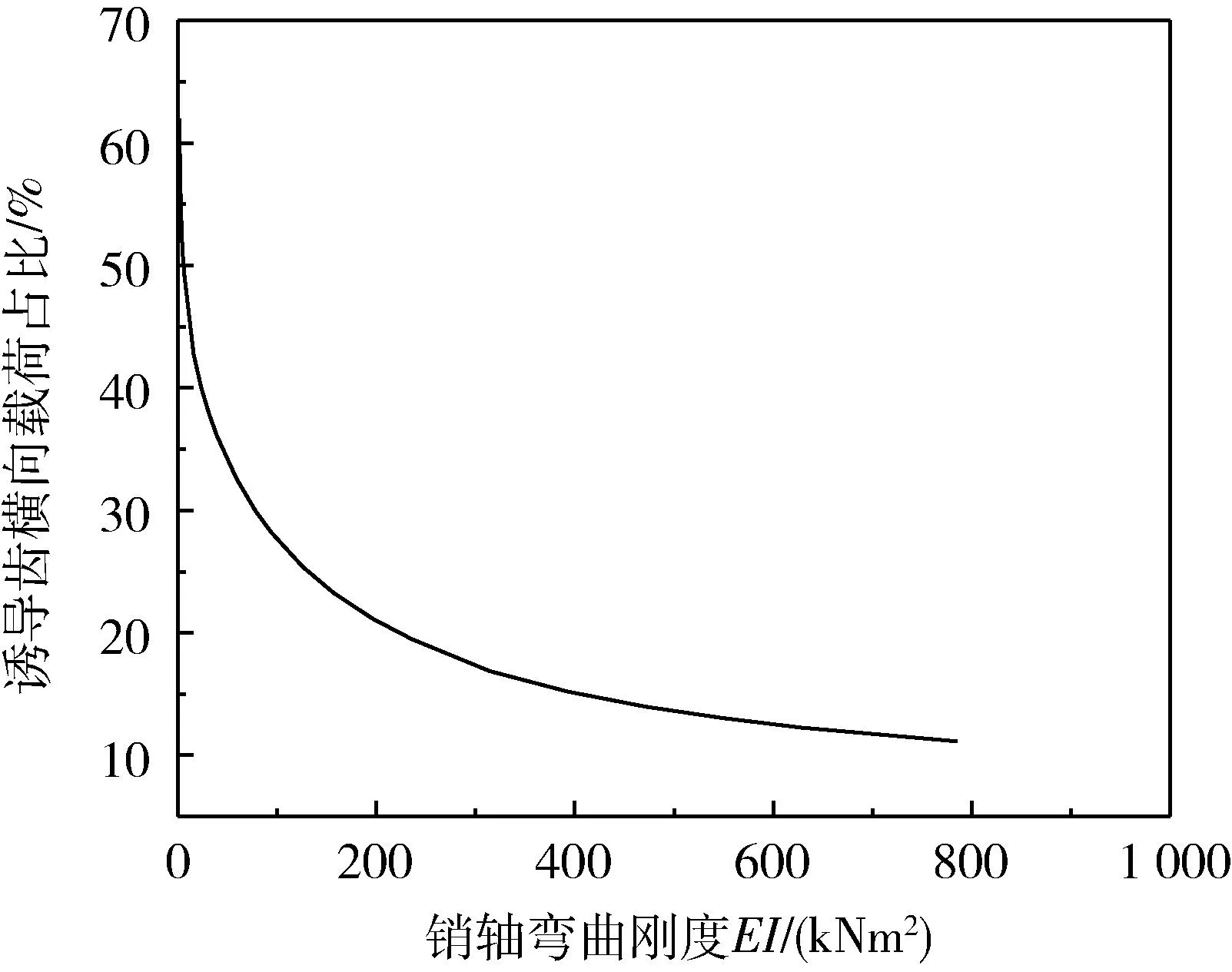
图7 诱导齿载荷分配占比与销轴刚度关系

由图7可知，随着销轴刚度增大，诱导齿横向载荷占比迅速下降，当销轴刚度不断增加直至视其为刚性轴，诱导齿所受拉力趋于定值.经分析可知通过适当增加销轴半径来增大销轴弯曲刚度从而减小诱导齿所承受的横向拉伸力.

1.4 连接部件结构尺寸对载荷分配的影响

(1)端联器结构尺寸影响

端联器结构示意图如图8所示，考虑端联器的销孔壁厚及其宽度对拉伸载荷分配的影响.通过改变端联器厚度与宽度，得到诱导齿载荷占比与端联器结构参数的关系，如图9所示.

图8 端联器结构参数图

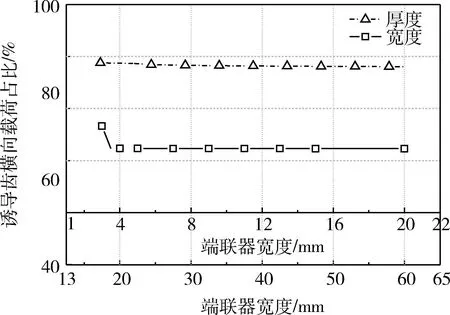
图9 端联器结构参数对载荷分布影响曲线

从图9可以看出，端联器厚度发生改变时，诱导齿所承受的横向拉力并无明显变化，其原因为增加端联器厚度虽能增加刚度，但在该刚度范围内对横向载荷分布的影响较小.当端联器宽度小于20 mm时，其对载荷分配的影响较为明显，宽度越小，端联器的刚度越小，从而导致诱导齿上载荷占比减少.

(2)改变诱导齿结构尺寸

诱导齿结构如图10所示.通过研究导齿盖壁厚和诱导齿宽度对拉伸载荷分配的影响，得到其关系曲线，如图11所示.由图11可知，导齿盖厚度与诱导齿宽度增加均可导致其刚度增大，诱导齿的横向载荷也随之增加.其中改变诱导齿宽度对载荷分配的影响更为显著.

图10 诱导齿结构参数图

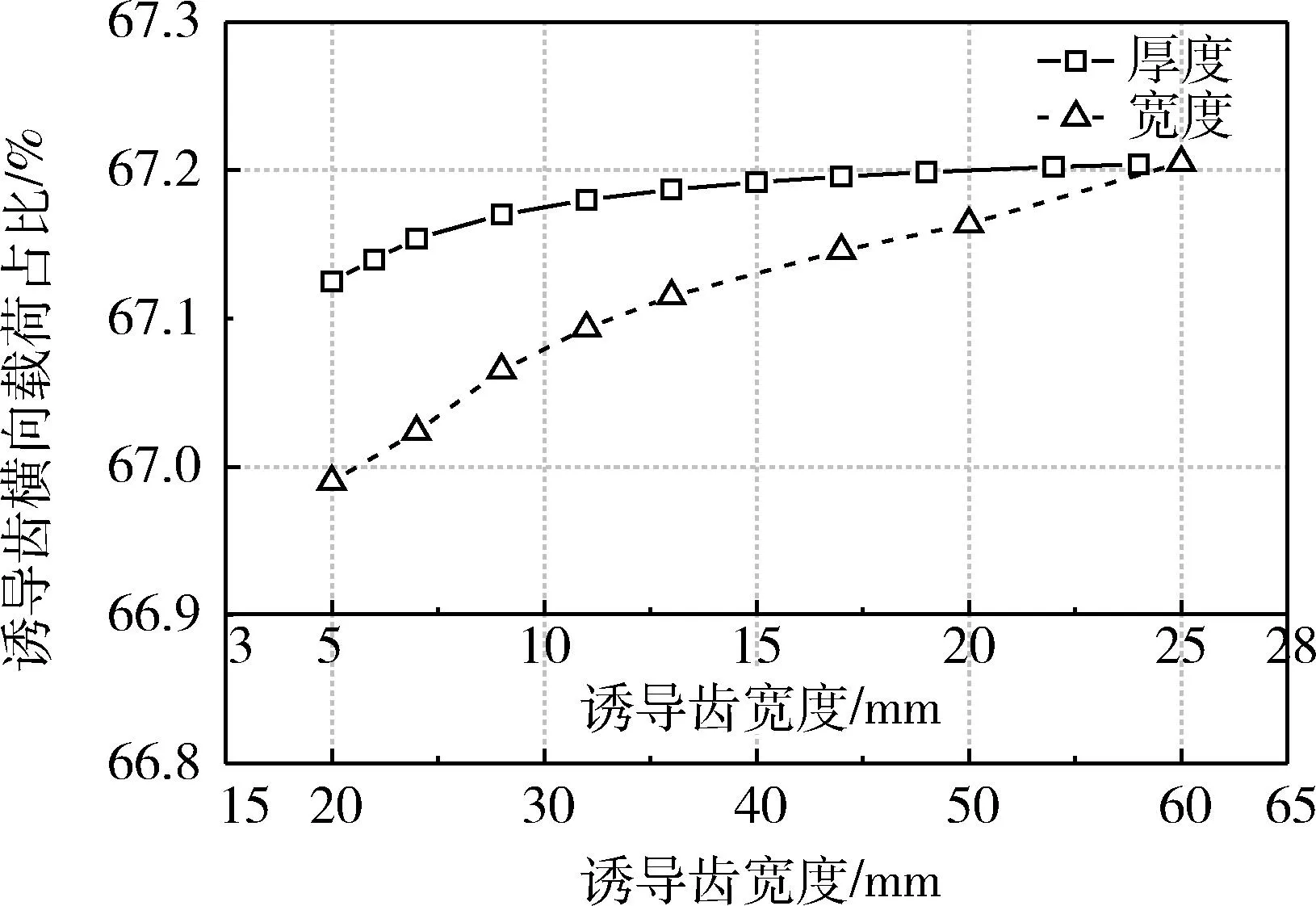
图11 诱导齿结构参数对载荷分布影响曲线

2 拉伸载荷下的履带板力学模型

在履带板拉伸工况下，拉伸载荷通过连接部件作用于销轴，并由销轴与销孔的配合传递到履带板板体，其二维模型受力图如图12所示.

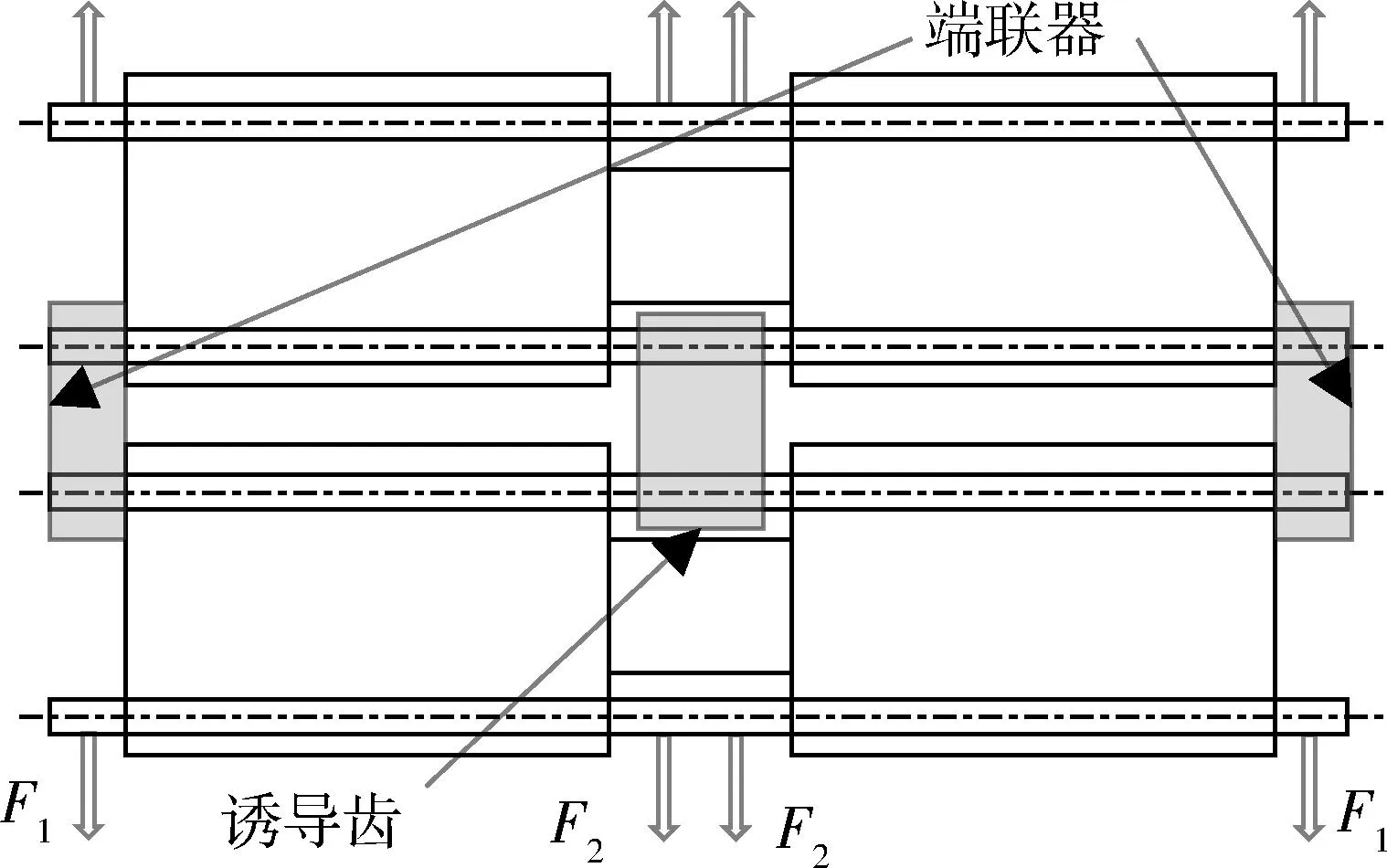
图12 履带板零部件受力示意图

考虑连接部件拉伸载荷F1、F2与各个零部件刚度的关系，建立单个销轴受力模型，如图13所示.销轴在拉伸工况下，受到连接部件和履带板体作用力，虚线为销轴受力弯曲变形后的二维示意图.经过受力分析后建立销轴力学模型.

图13 销轴受力示意图

2.1 刚性销轴模型

将销轴视为刚性轴，无弯曲变形，此时，诱导齿与端联器等效弹簧的拉伸变形长度相等，x1=x2，分别定义端联器和诱导齿的连接刚度为K1、K2，可得到两者横向拉伸载荷与刚度的关系式：

(3)

由于弹簧变形长度相等，故得到

(4)

得出端联器与诱导齿拉伸载荷占比等于两者刚度比，在模型中，K1/K2≈15，即F1/F2≈15.刚性销轴模型虽为简化模型，但分析仍可得出当连接部件刚度增大时，其相应会承受更大的横向载荷.

2.2 考虑销轴变形的模型

为得到更真实的理论模型，考虑销轴弯曲变形对载荷分配的影响.销轴非刚性，通过材料力学计算出销轴在各边界条件下的挠度.对销轴进行分析简化，将其所受到连接部件和履带板体的力等效至每个受力段的中心点处，如图14所示，根据履带板的对称性可知，履带板体所施加在销轴上的合力为2F1+2F2，并分别通过橡胶衬套作用于轴上.

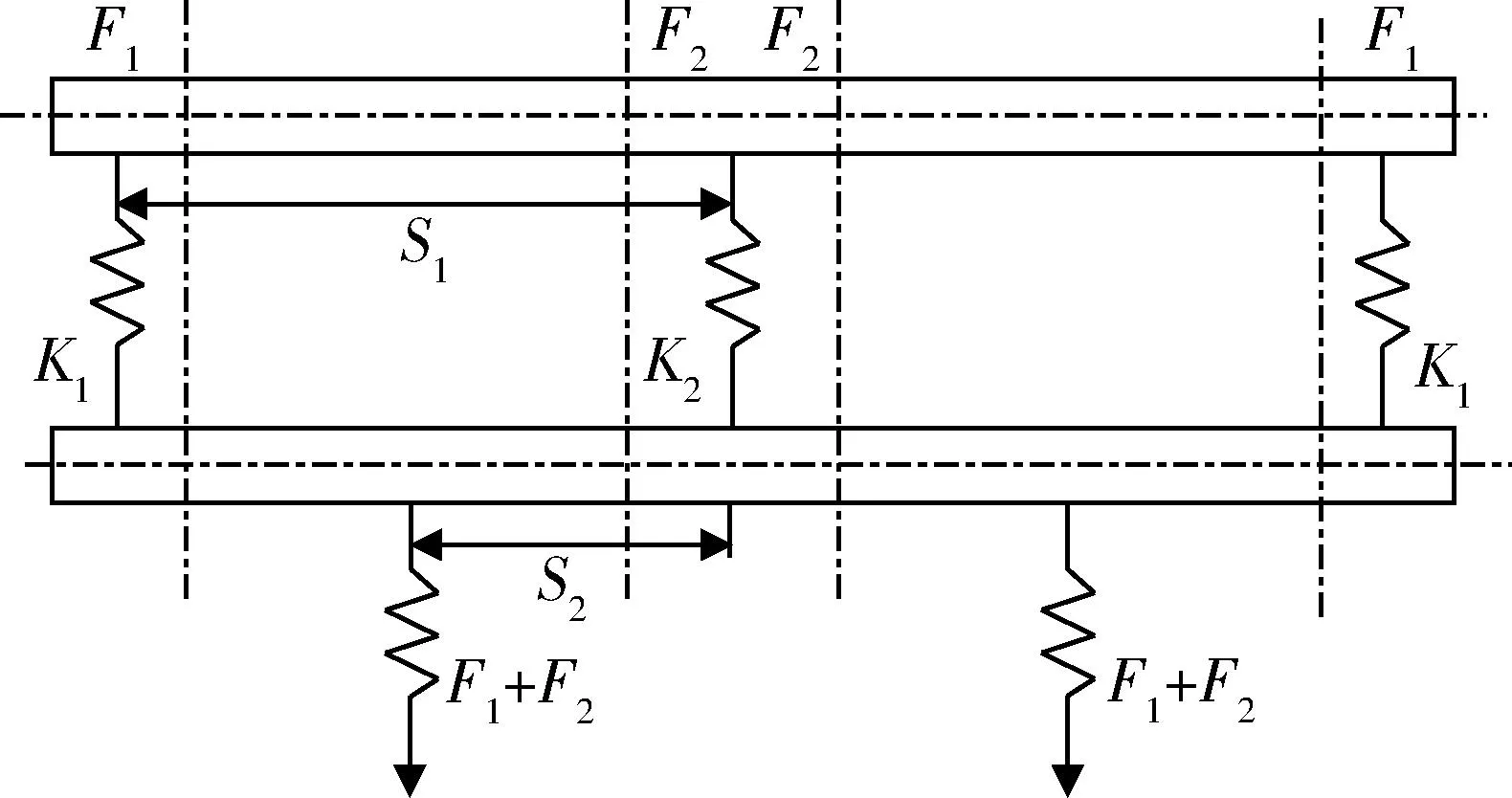
图14 销轴载荷施加示意图

将履带板体视为刚性板，端联器与诱导齿在以销孔为基准时两者端面的位移相同，故得到：

(5)

式中：ω1为端联器载荷作用中心点挠度；ω2为诱导齿载荷作用中心点挠度.

根据材料力学挠度杆公式[12]，得到两者挠度关系.

(6)

式中：E为销轴弹性模量，150 GPa；I为销轴截面惯性矩.

联合上式可得到：

(7)

得到端联器与诱导齿横向载荷之比F1/F2：

(8)

从(8)式得出，连接部件的载荷分配受到端联器、诱导齿刚度的影响，同时也与销轴弯曲刚度和连接部件载荷作用中心点位置有关.在本次探究中，履带板结构已确定，即S1，S2不变，只考虑K1、K2、EI对载荷分配的影响.当销轴的弯曲刚度EI趋于∞时，销轴被看成刚性杆，连接部件载荷分配变为K1/K2，与刚性杆模型结果相同.在本模型中，S1=144.25 mm，S2=74 mm.将相关参数带入到上式，求出载荷分配比例：

诱导齿与端联器横向载荷比为F2/F1=2.02.从而得到诱导齿的载荷占比为66.89%，单个端联器的载荷占比为16.56%.

通过理论解与有限元计算结果(61.99%)相对比可知两者间具有一些误差，其原因是在计算理论模型的载荷分配时，将连接部件的横向载荷作用于接触区域的几何中心处，其与实际有限元施加的等效合力中心位置有所不同，且在计算端联器、诱导齿刚度时使用平均位移变形作为等效弹簧单元的拉伸变形，此时也会产生误差.

分析诱导齿与端联器横向载荷比公式，得到载荷占比与连接部件刚度和销轴刚度的关系，其与连接部件刚度的关系如图15所示.

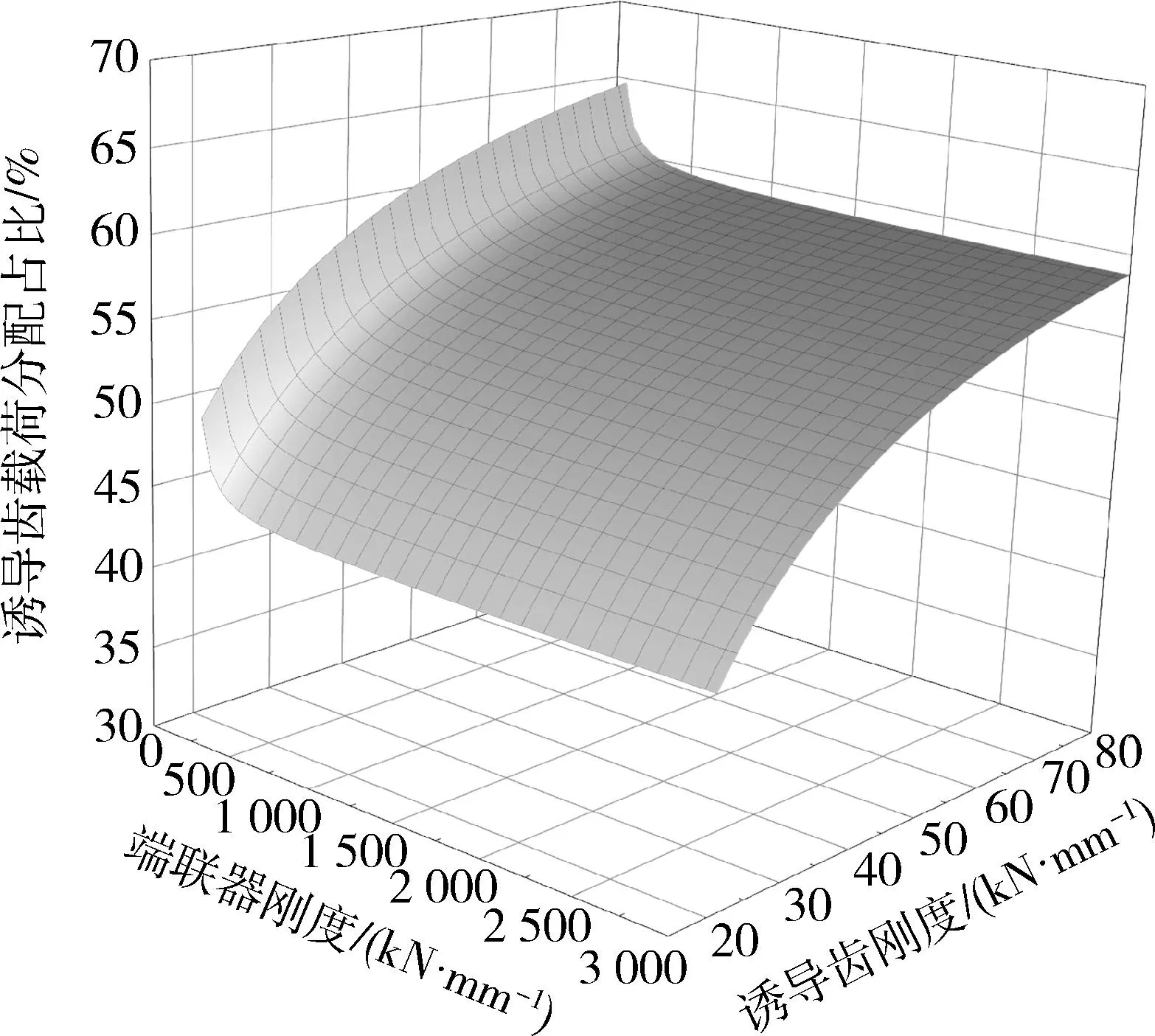
图15 理论模型诱导齿载荷分配曲面图

图15与图5比较可知，在有限元模型和理论模型中，连接部件刚度对横向载荷分配的影响规律相同，两者结果吻合，由此得出在计算拉伸载荷分布时有限元模型仿真计算结果的准确性和可信度，诱导齿刚度较小却承受较大的载荷占比，通过载荷分配影响因素的分析，可以采用减小诱导齿刚度、增大端联器刚度的方法减小诱导齿横向载荷占比，使其应力减小，降低失效风险.

对理论模型中拉伸载荷分配与销轴弯曲刚度的关系进行分析，连接部件刚度为定值，通过改变销轴弯曲刚度进行计算，将理论结果与仿真结果进行对比，如图16所示.可知，销轴弯曲刚度增加，诱导齿横向载荷占比减小，当销轴刚度增加至其被视为刚性杆时，诱导齿横向载荷占比趋于定值.理论模型载荷分布规律与有限元计算中销轴刚度对横向载荷占比的影响规律相同，由于理论模型中忽略了履带板板体的横向刚度等，两者存在误差且小于5%.

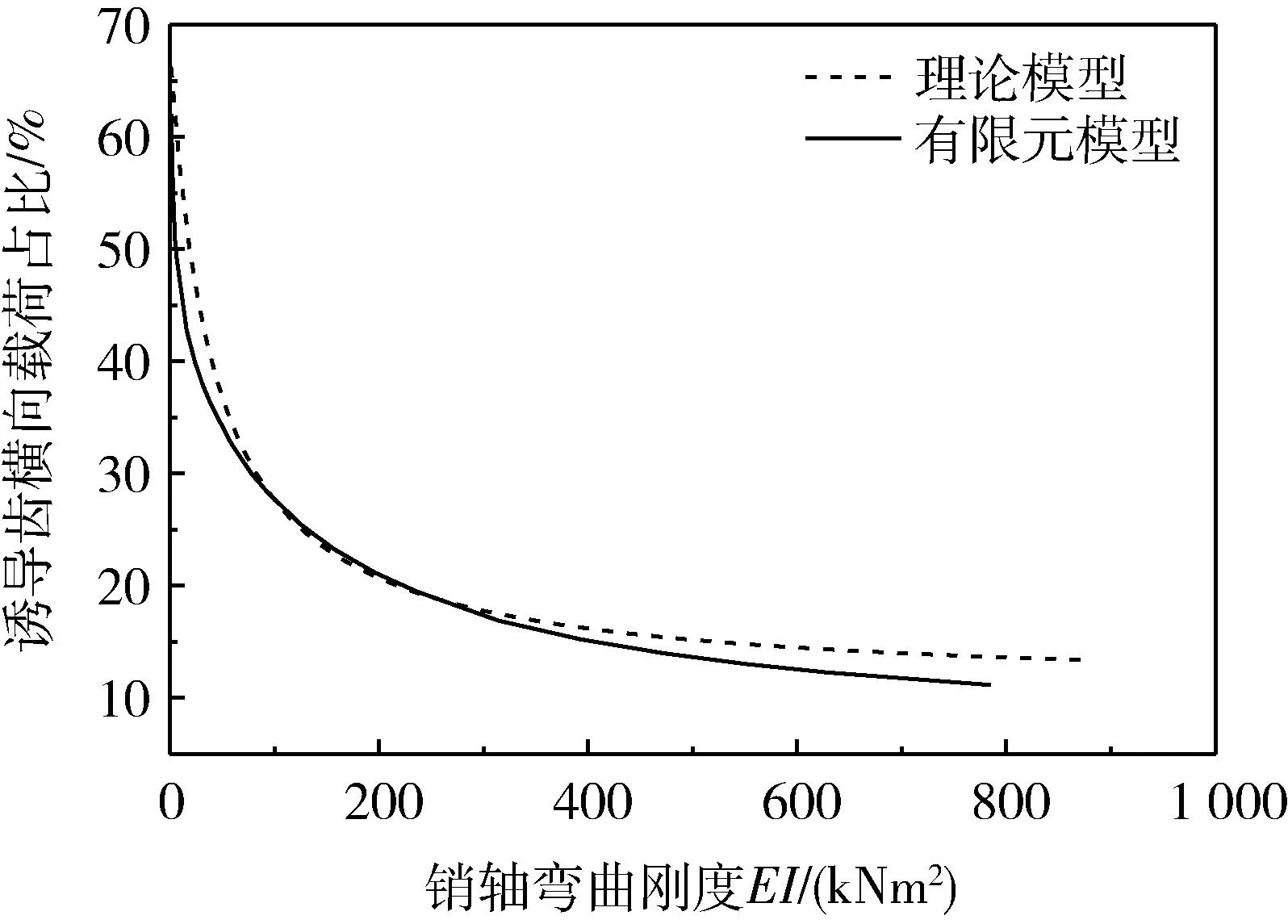
图16 理论模型与有限元模型横向载荷分配占比结果比较

3 结 论

文中计算了履带板在最大牵引力工况下连接部件的载荷分布情况，通过有限元计算得出载荷分配与端联器、诱导齿和销轴刚度的关系，并使用力学模型得到理论数值解，验证有限元仿真计算结果的准确性及其可信度，得到以下结论：

1)在最大拉伸载荷工况下，诱导齿拉力占比随端联器刚度的增大以及诱导齿刚度的减小而减小，但并非线性关系；

2)当连接部件的刚度比为定值时，诱导齿的刚度越小，诱导齿的横向载荷分配占比也越小；

3)当销轴弯曲刚度不断增大直至被视为刚性杆时，诱导齿横向载荷占比则不断减小，故可通过增加销轴轴径来减小诱导齿所受拉力；

4)在采用两步法进行拉伸载荷的迭代计算时，有限元模型具有准确性，理论模型验证了仿真结果的可信度.